基于Beta族的相关贝叶斯模型在准备金中的应用
刘 燕,李云瑞
(1.郑州大学 数学与统计学院;2.河南省金融工程重点实验室,郑州 450001)
0 引言
未决赔款准备金是保险公司为将来未决赔款的赔付提前计提的准备资金,计提充足的未决赔款准备金是维护投保人权益和保障保险公司正常的偿付能力的重要工作。在我国,非寿险保险公司准备金的提取大多使用传统的估算方法,比如链梯法,案均赔款法,B-F方法等。这些统计类方法使用比较简单,但没有重视随机因素的影响,准确度并不很高。
由于各种保险特征因素的影响,如索赔频率、索赔额度及理赔方式,都会使各进展年索赔额之间具有一定的相关性,因此就会导致使用独立假设下的贝叶斯模型来估计未决赔款准备金时,与实际准备金的支出额有较大偏离。因此,需要考虑增量赔款的相关性对未决赔款准备金评估模型的影响。Gilks等(1995)[1]在模型中通过一个潜在过程来构造相关Gamma过程,并应用此相关Gamma过程来体现事故年之间的相关性。由于Beta族分布类是比Gamma分布更广的分布类型,Gamma分布仅仅是Beta族分布类的一个特例,所以本文将Gamma过程推广到Beta族分布类来建立未决赔款准备金评估模型。下面给出基于Beta分布类的相关过程的理论模型,并对其中的相关参数使用贝叶斯估计。本文假设事故年i和进展年j的增量赔款额为Xij,即第i个事故年发生的索赔在第j个进展年的所有赔款。但对于不同的流量三角形中不同的事故年i和i′(i≠i′),未决增量赔款过程和是相互独立的。
1 基于Beta族的相关贝叶斯模型
一般假设Beta分布族的分布密度函数为:
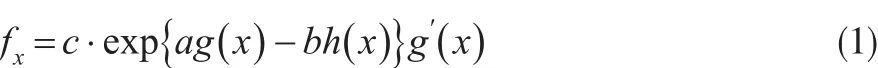
这里a、b、c为常数,h(x)、g(x)均为x的可导函数,且满足性质h′(x)g′(x)=x。
假设增量赔款Xij服从Beta族分布,即对所有的i有,Xi1密度函数为:
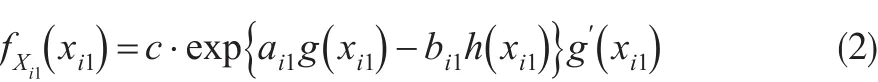
Zij|Xi,j-1的密度函数为:
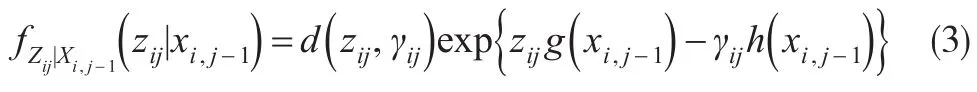
并且有:
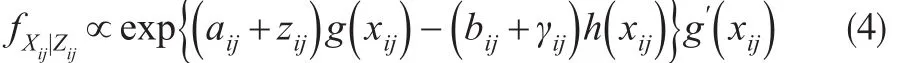
由以上的构造过程可以发现,保单组合的第i个事故年的增量赔款额Xi,j-1和Xij通过潜在的过程Zij建立了相关性,并且可以证明其具有下面的性质:
定理1:保单组合的第i个事故年的增量赔款额Xij为Beta族分布,且过程是Markov过程,则有如下性质:
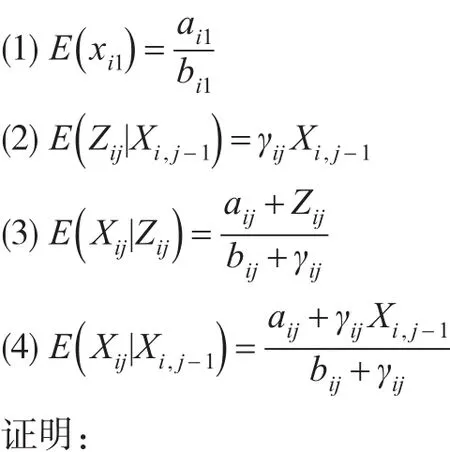
(1)由分部积分法得:

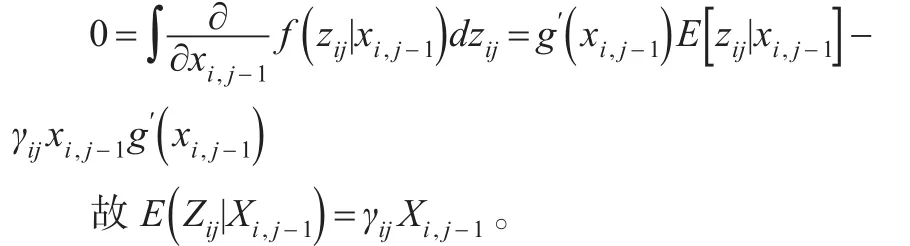

其中,ai为赔款的平均总额,bj为增量赔款占赔款平均总额的百分比:

由式(6)可知λj∈( )0, 1 ,j=1, 2, … ,n,从式(5)可以得到,Xi,j在Xi,j-1条件下的期望是第 i个事故年的增量赔款额Xi,j的期望值和前一进展年的增量赔款额Xi,j-1的以λj为权重的加权平均。其中λj越大Xi,j和Xi,j-1的相关程度越强。若有γj=0 ,则Xi,j和Xi,j-1的相关程度为0,此时相关贝叶斯模型就退化为独立的贝叶斯模型。
2 相关贝叶斯模型的参数估计
使用相关贝叶斯模型计算未决赔款准备金时,首先需要根据贝叶斯方法[2]估计其中的参数,ai、bj和λj。令:

首先,假设各参数的先验分布为:
其次,在上面的假设下,可以得到变量X,Z的联合分布。
定理2:假设未决增量赔款Xi,j服从Beta族分布,其流量三角形中上三角的所有变量X,Z的联合分布满足:

最后,应用贝叶斯原理,可以得到未决赔款分布中各参数的后验分布如下定理3所述:
定理3:未决赔款额增量赔款分布中参数满足下列性质:
(1)参数ai的条件后验分布:对于所有的i=1, …,n有:
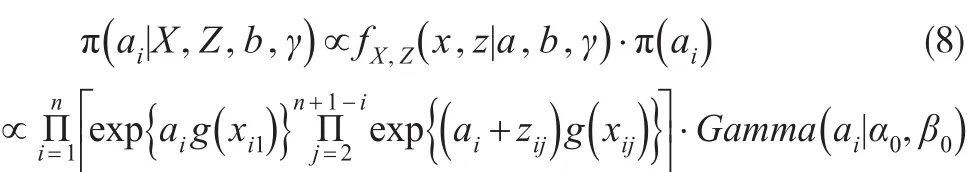
(2)参数bj的条件后验分布:
①当j=1时有,
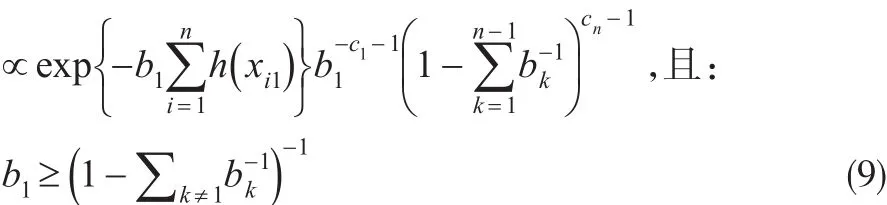
②当j=2, …,n-1时有:
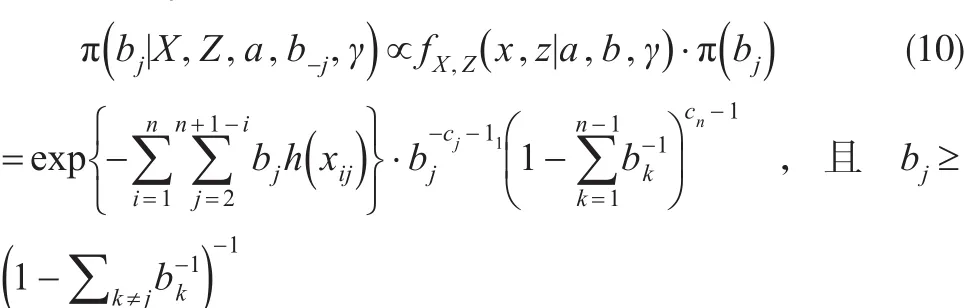
③当j=n时有:

(3)参数γj的条件后验分布:对于所有的j=2,…,n-1有:

模型中参数后验均值的计算比较复杂,可以应用数学软件分析其数值解,再抽样得到后验分布的样本,在此基础上分析参数的后验均值。
3 未决赔款准备金的预测
在流量三角形中估计未决赔款准备金,需要预测未决增量赔款流量三角形中未来未决赔款的增量的大小,本文假设上三角已知的增量赔款Xij(i=1, …,n,j=1, …,n-i+1)和需要预测估计的下三角中的未决增量赔款有相同的分布形式,根据Zij在条件X下的分布:

可以进一步得到增量赔款的概率密度函数:

若对所有的i=1, …,n,有,则在条件下的预测分布有如下形式:

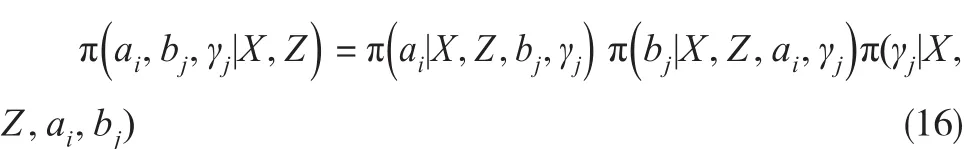

4 预测模型的评价
由于在相关贝叶斯模型中不适合使用方差,均方误差等指标来评价模型的优劣。Ibrahim和Laud[4]于1994年提出L测度,测度值L()x是方差和偏差的组合,他的大小可以体现模型预测的误差,具体形式如下:
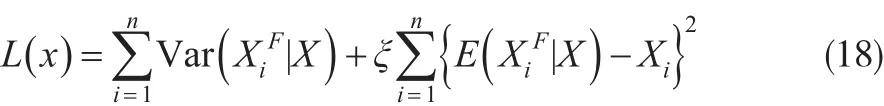
5 实证研究
模型中考虑的流量三角形均为增量赔款流量三角形,使用Taylor和Ashe所给的未决增量赔款数据集,本文假设未决增量赔款随机变量Xij服从伽马分布,为了对比模型预测未决赔款准备金的情况,可以分别应用独立Gamma过程和相关Gamma过程来预测未决赔款准备金,分别将两个模型的估计结果进行比较和分析(见表1)。这里应用R软件[5]实现预测模型,并通过Gibbs抽样[6]的方法来估计其中的参数。
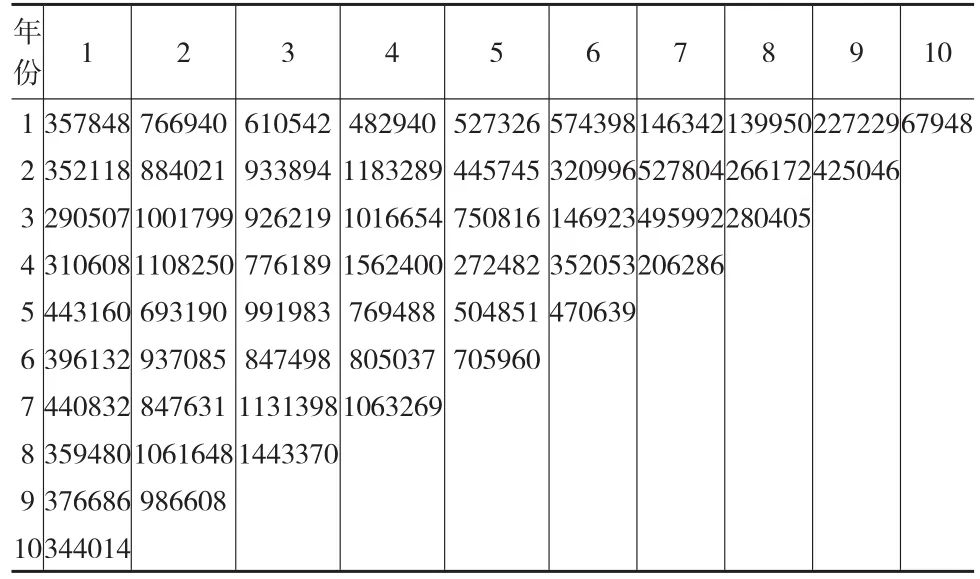
表1 增量赔款流量三角形
首先应用独立贝叶斯模型[7]来预测未决赔款准备金,即Xij是相互独立的。
a=(4.168, 5.925, 5.5013, 5.0212, 5.7365, 5.9001,6.4997, 7.2953, 6.2659, 5.4173),(以百万为单位),
1b=(0.04, 0.15, 0.18, 0.17, 0.10, 0.08, 0.07, 0.05,0.08, 0.03)
由以上估计的模型参数的后验均值,可以估计增量赔款流量三角形下三角的数据和各事故年的未决赔款准备金,通过R语言编程实现模型,可以得到结果如下页表2所示。
表2给出了所有事故年在各个进展年的增量赔款额和各事故年的未决赔款准备金,再对各事故年的准备金求和,即保险公司所需计提的未决赔款准备金约为2132万元。

表2 独立贝叶斯模型增量赔款和准备金估计值
然后应用相关贝叶斯模型来预测未决赔款准备金,即Xij是相关的。
对所有的i有:

这里需要估计的参数有αi,βj,γj,给定参数的先验分布为:
αi~Gamma( )0.001, 0.001,β~I-Dir(1, …,1),γj~Gamma( )0.01, 0.01
α=(5.1714, 7.4139, 6.3995, 5.4037, 7.4706,7.8652,8.4857, 9.0457, 7.9534, 6.6329)(百万)
1β=(0.06, 0.28, 0.15, 0.16, 0.07, 0.06, 0.05, 0.04,0.06, 0.02)
λ=(0.70, 0.65, 0.66, 0.13, 0.03, 0.02, 0.02,0.01, 0.01)
由以上估计的各参数的后验均值,可以估计增量赔款流量三角形下三角的数据和各事故年的未决赔款准备金,通过R语言编程实现,得到未决赔款准备金如表3所示。
表3给出了所有事故年在各个进展年的增量赔款额和各事故年的未决赔款准备金,再对各事故年的准备金求和可得总的未决赔款准备金为2061万元。
分别对ξ=0, 1 2, 1三个不同的取值分别计算两种模型估计未决赔款准备金的L测度值:由表4可知,相关贝叶斯模型的L测度在各种ξ取值下估计的误差值都比独立贝叶斯模型的L测度值要小。显然,针对这个实例估计的未决赔款准备金,使用相关贝叶斯模型估计的值更准确合理。
6 结束语
本文将Enrique de Alba和Luis E.Nieto-Barajas(2008)提出的相关贝叶斯模型中增量赔款的分布推广到Beta分布族,建立基于Beta族分布的未决赔款准备金评估模型。在此理论基础上,使用流量三角形来预测保险公司所需计提的未决赔款准备金。并使用R软件编程实现准备金的随机评估模型,通过Gibbs抽样估计模型中的参数ai、bj和λj,计算未决赔款准备金的估计值和估计偏差的L测度值,分析估计值的性质和优劣。但文中没有考虑各事故年增量赔款之间的相关性,而且抽样统计分析也还存在一定的误差,这些问题都还有待于进一步的研究。

表3 相关贝叶斯模型增量赔款和准备金估计值

表4 两种模型的L测度值比较

