EMD与温度剔除方法在桥梁应变处理中的应用研究

楼 文 祺

(浙江工业大学，浙江 杭州　310014)

目前针对桥梁非稳态信号处理的方法主要有短时傅立叶变换、Wigner-Ville分布、小波分析等，这些方法却不能与HHT方法一样得出信号频率的确定表达式，达到对非稳态信号处理过程优化的目的。从大量的实验结果看，用于提取信号发展趋势或者是信号均值的最佳方法就是其中的EMD方法。EMD方法作为新兴的分析工具，在吸引大量专家学者对其进行研究的同时，也已被广泛应用于土木领域。但由于监测对象的相异性，EMD方法在数据处理方面仍具有非常大的研究前景以及进一步的应用价值。本文将EMD方法结合温度应力剔除方法对嘉兴某桥的健康监测系统采集到的桥梁动应变数据进行处理，以探讨其在桥梁信号中的应用问题，见图1。

1　EMD数据处理方法研究

1.1　EMD处理方法

原信号经EMD分解后的表达式为：

(1)

其中，Re[·]意为只取实部；ci(t)为各阶IMF分量。

用上述三种组合方法对相同的若干组应变信号进行处理，得出处理后的信噪比，如表1～表3所示。

表1　方法一信噪比　dB

表2　方法二信噪比　dB

表3　方法三信噪比　dB

由表1～表3可知，对于本次试验测得的桥梁动应变信号，采用方法三处理数据所得到的信噪比要高于其余两种方法，因此针对本次试验信号，将采用该方法对其进行处理。

1.2　端点效应方法

在用上述EMD方法处理数据时，采用极值点预测法解决提取IMF时易产生端点效应(end effect)的问题，即统计实际工程中应变信号的极值点分布规律拟合成集，作为添加新极值点的科学依据。

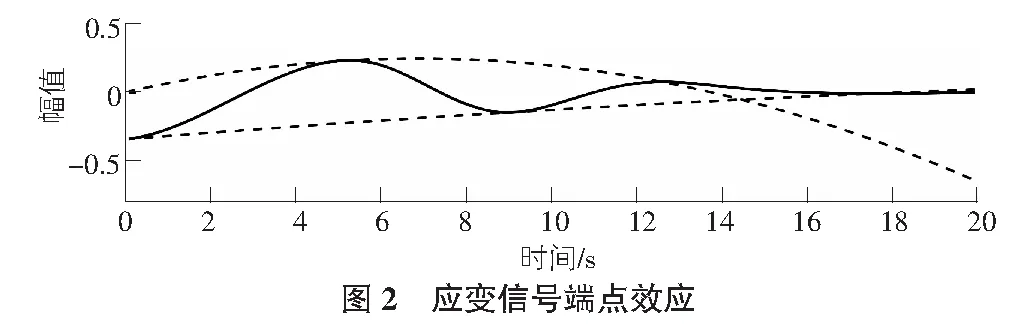
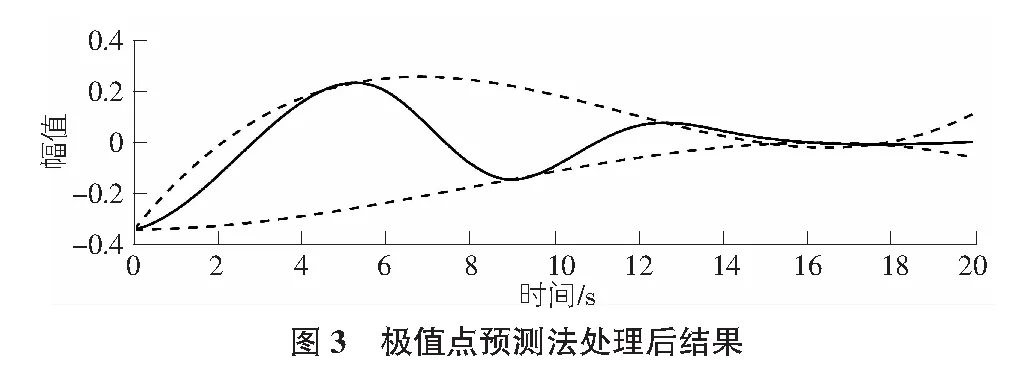
对比图2，图3中显示的包络线拟合结果，可以看出，采用极值点预测法对端点效应进行处理后的三次样条曲线拟合效果还是非常理想的。

2　动应变参数处理

2.1　温度效应剔除方法

本文将文献研究成果与试验采集到的大量数据结合，利用温度与应力间的强关联性，通过线性拟合方法得到了适应于该桥梁健康监测系统的温度应力拟合函数，结果表达式如式(2)所示：

(2)

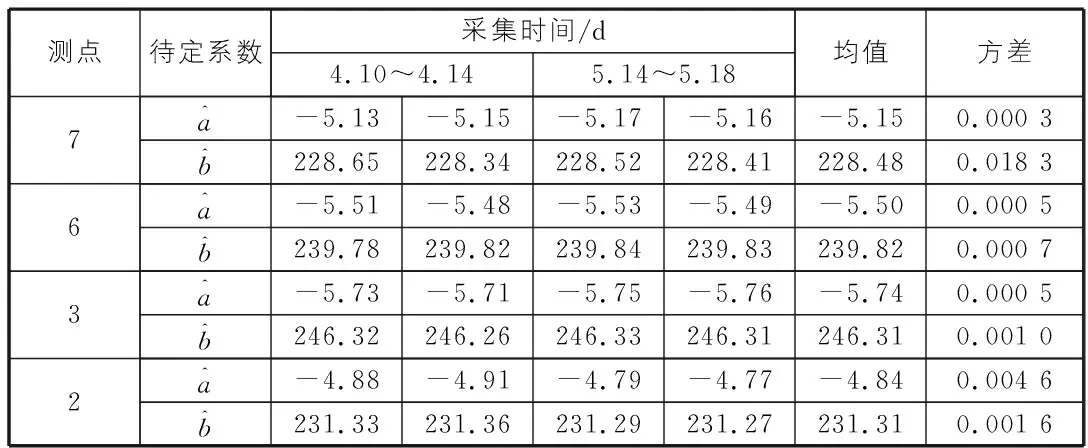
表4　待定系数拟合结果

2.2　应变处理结果

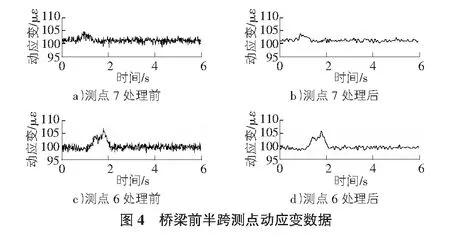
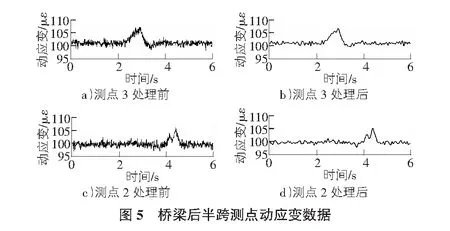
在桥梁上进行单车行车试验，试验车重为10 t，行车速度为30 km/s，依次经过测点7,6,3,2。整理传感器采集到的应变数据并将EMD处理方法和温度效应剔除方法结合应用于对其的处理过程中，实测数据和处理后数据如图4，图5所示。

从图4，图5中可以看出，处理前的桥梁无载时动应变波动区间为96.61～102.77，单车过桥时峰值为106.83，结合温度效应剔除方法和EMD方法处理后，动应变波动区间为98.56～101.69，峰值为106.71。结果表明，用该组合方法处理应变数据能保留数

据的主要特征，同时明显增加数据的平稳性，有利于对桥梁构件的损伤识别。

3　结语

本文通过对嘉兴某桥的桥梁健康监测数据进行处理，讨论了应变数据EMD分解后的IMF的重组方式，结合MATLAB数值模拟结果和实测数据信噪比的分析结果，得出适用的EMD方法。分析温度应变关系，利用线性回归结果，得到温度效应剔除方法。将两种方法组合应用于应变数据处理中，结果表明，这种处理方法能使数据更为平稳，在保留数据特征的同时能进一步分析判断出构件的损伤位置。