大学物理热学教学的几点释疑
郑文珍
(衢州学院教师教育学院,浙江 衢州 324000)
热学是理工科大学物理教学中的基本内容之一[1],它的基本理论和研究方法对提高学生的基本科学素养、增强逻辑思维和分析判断能力、深刻把握宏观世界的微观机理等都有着其他课程无可替代的作用;对现代科技发展的物理支撑和新技术、新材料的开发应用也有着十分重要的意义。但由于热学内容是学生第一次接触到用宏观实验规律和微观统计理论两种思维方式处理具体物理问题,概念众多,思维跳跃性大,看似几块独立的内容而又相互关联、相互制约,要弄清这些问题,对大学一年级的学生来说,确实存在着较大的难度,甚至无所适从。如何解决这个矛盾,帮助学生更直观地明了热现象的物理本质、建立起更明晰的热物理图像、突破学习中的困惑和难点,也就成了热学教学中一个十分紧要的问题。在实际的教学过程中,笔者针对学生出现的困难,在充分强调对基本概念理解的同时,对部分内容作了一定的拓展或延伸,重点释疑,使学生能从不同角度理解热现象的物理本质,强化了学生对宏观与微观之间物理本质联系的理解,收到了较好效果。下面略举几例予以说明。
1 最概然速率vp与最概然动能εp的关系
由麦克斯韦气体分子按速率分布规律,在温度为T的平衡态下,理想气体分子的最概然速率vp定义为与速率分布函数f()v的极大值相对应的速率。它表明,若把气体分子的速率等间隔划分,即取Δv一定,则理想气体在该温度下分布在vp附近单位速率区间内的分子数最多,容易得出[2]


也就是说,与最概然速率vp所对应的分子动能为k T。
但由麦氏分布律,很容易导出气体分子按动能的分布规律为[3]
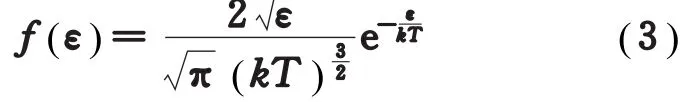

比较式(2)和式(4) ,显见,与最概然速率vp所对应的动能ε(vp)并不等于最概然动能εp。原因何在?面对这一矛盾的结果,学生往往感到茫然。仔细分析不难发现,出现上述矛盾结果,其核心就在于是对哪个物理量取间隔,亦即是d v还是dε。f(v)是在速率v附近单位速率区间内的分子数占总分子数的比率,是对速率v取间隔;而f(ε)则是在能量ε附近单位能量区间内的分子数占总分子数的比率,是对能量ε取间隔。上述两种分布函数中的最概然值是对不同的统计间隔而言的,因而得出了不同的结果。所以我们在讨论统计分布函数的最概然值时一定要强调是对什么统计间隔而言的[4],否则就会出现理解上的困难或概念上的不自洽。明白了这一点,上述问题也就从根本上得到了解决。
2 对η=1-的非近似证明
几乎所有的大学物理教材在推导卡诺循环效率时都是利用理想气体状态方程、热力学第一定律及绝热过程相关方程得到这种方法物理过程清晰、简明易懂,很容易解决教学上求热机效率的方法问题。但细究起来又出现了一个疑点:在作上述推导时都假定了热容量C和绝热指数γ皆为常数这一条件,但C实际上是一个与温度有很大关系的物理量[2]。因此,从严格意义上来说上述推导结果只是一个近似的结果。在实际教学中,笔者在讲述了上述推导方法后,又给出了一个改进的证明,就是在证明过程中只利用热力学第一定律和理想气体状态方程,而并不直接出现热容量C和绝热指数γ,从而避免了本是精确结果却被近似化的尴尬。
如图1所示的卡诺循环,对1 mol理想气体,p V=RT,即有p=。在a→b等温膨胀过程中,系统吸热,对外做功。系统吸收的热量为

在b→c绝热膨胀过程中,系统内能减少,对外做功,所做的功为Wb→c=u( T1)-u( T2)。在c→d等温压缩过程中,外界对系统做功,系统放热Q2=|Wc→d|。系统所做功为
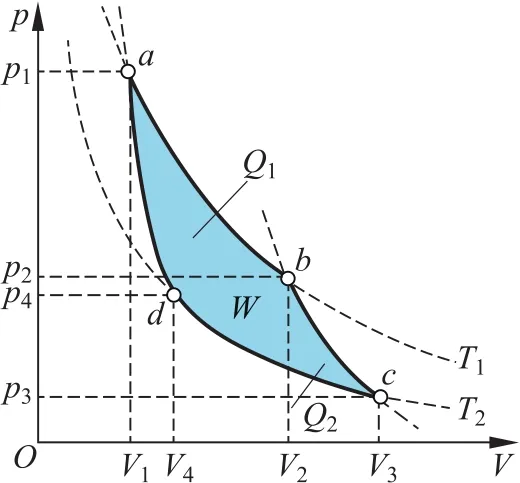
图1 卡诺循环

在d→a绝热压缩过程中,外界对系统做功,系统内能增加。系统做功为Wd→a=u( T2)-u( T1)。
在一个循环过程中系统对外所做净功为W=Wa→b+Wb→c+Wc→d+Wd→a,故
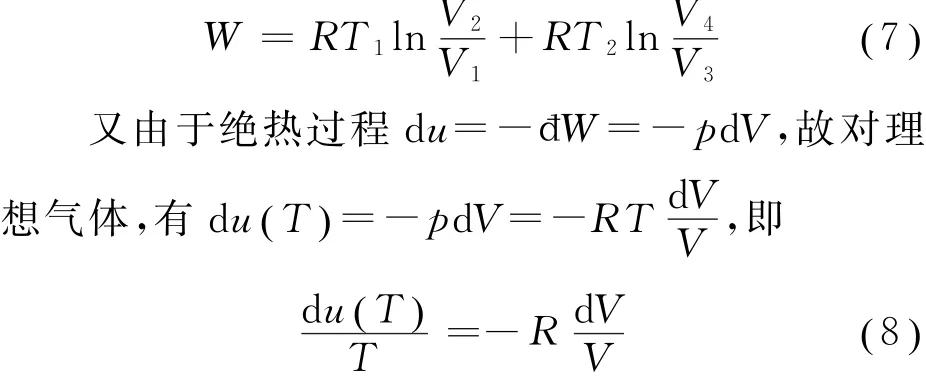
考虑到绝热过程b→c和d→a,由式(8),可得
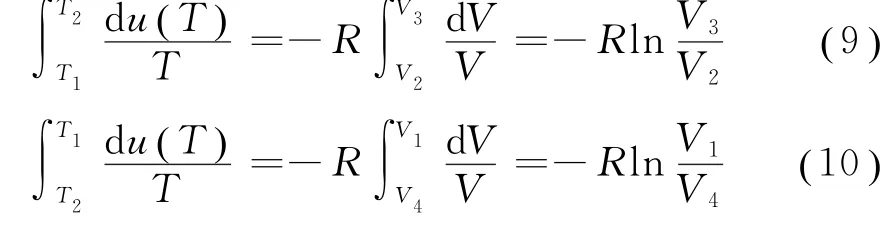
对于一个循环,其特征是系统的内能不变。而在卡诺循环中,两个等温过程系统的内能不发生改变,所以有

将式(11)代入式(7),得到
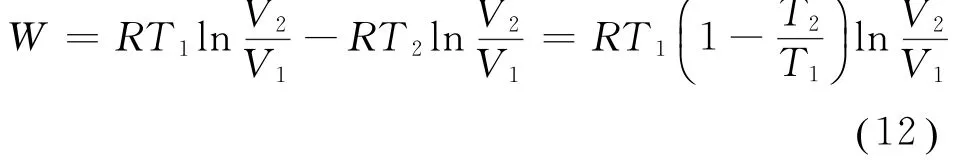
从而由式(12)及式(5),可得卡诺循环的效率为
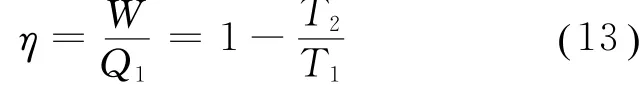
其结果与各教材结果一致。
但在以上证明中,因未直接应用热容量C和绝热指数γ,故不用考虑具体的随温度变化的相关C和γ值,也就舍去了C和γ不随温度变化这一近似性前提,其结果也就显得更有说服力。
3 范氏气体的内能和热容量
在众多的实际气体物态方程中,范德瓦尔斯方程是最早和最有影响力的实际气体物态方程[8];且因其形式相对简单、物理意义明确而受到广泛应用,并由此建立了低温物理学,在今天的节流效应中也有广泛的应用[9]。
对于1 mol范氏气体,其物态方程为
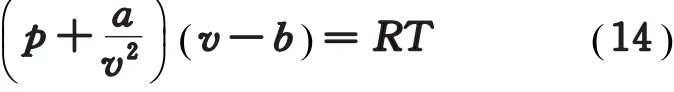
式中,a、b为范氏修正量;v为气体的摩尔体积。
(1)内能
在考虑了气体分子引力和体积的情况下,范氏气体在膨胀时不仅要反抗外力做功,还要克服分子间的内引力做功,此内引力即为分子之间的吸引力。对1 mol范氏气体,其由分子吸引力产生的内压强为当气体膨胀时,此内力所做的功为đW=此功即为势能的增量d EP,则
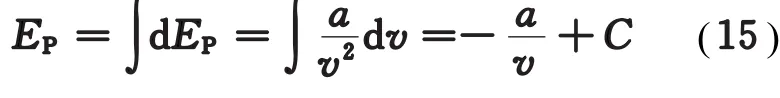
式中C为积分常数,若取v→∞时EP=0,则C=0,所以

由于气体分子作无规则热运动的动能只与温度有关,故1 mol范氏气体分子作无规则热运动的动能与1 mol理想气体分子的动能相同[3],只由温度决定,即EK=CV,mT。故对于1mol范氏气体,其内能为

上式表明,以范氏气体为代表的实际气体的内能由温度T和体积V共同确定,u=u(v ,T)。当实际气体的内能保持不变时,体积的膨胀必然导致温度的降低[10],从而促成了节流制冷效应的实现。
(2)范氏气体的热容量
考虑1 mol范氏气体,根据热力学第一定律及式(18),它在一个物态变化过程中所吸收的热量为
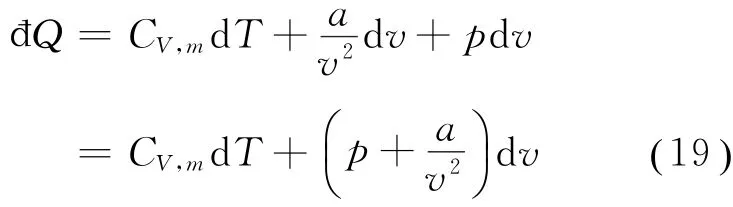
在一个等体过程中,v=常数,d v=0,故đQV=d u=CV,md T,所以
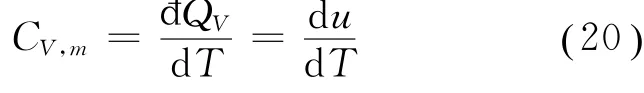
由式(20)可知,范氏气体的定体摩尔热容量CV,m与理想气体的定体摩尔热容量相同,是内能对温度的一阶导数。如果忽略温度变化对热容量的影响,则范氏气体的定体摩尔热容量亦为一常数。
而在定压情况下,对于1 mol范氏气体,đQp=其定压摩尔热容量C,为pm

对式(14)两边取微分,并注意到p=常数,可得
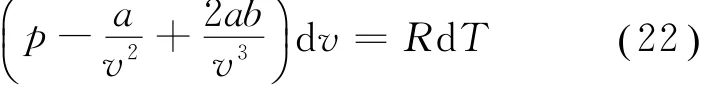
结合式 (14)、(22)进行化简,可得 đQp=代入式(21),从而得到范氏气体的定压摩尔热容量为
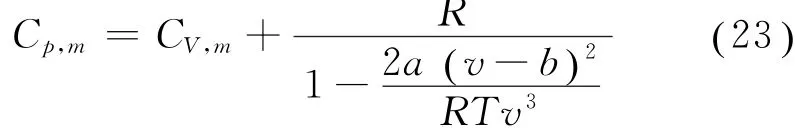
式(23)表明,对于范氏气体,其定压摩尔热容量并不满足理想气体所遵从的迈耶公式Cp,m=CV,m+R,也不再是一个常数,而是一个与温度和体积直接相关的量,并且与温度和体积呈现相对复杂的非线性关系。

