费恩曼的10大贡献及教学启示
包景东
(北京师范大学物理系,北京 100875)
诺贝尔物理学奖获得者、美国加州理工学院理论物理教授理查德·费恩曼先生于1988年2月16日,因病与世长辞,2018年是这位伟大的物理学家诞辰100周年。费恩曼思想的光辉指引着后人:“不做世界的观光客,而是科教的探险者。”打开Web of Science网,搜索作者名Feynman P R,显示费恩曼共发表了48篇论文,截止到2018月3月14日(雅称π日,伽利略的忌日、爱因斯坦的诞辰、霍金的忌日),费恩曼的论文被引用次数为27496,平均每篇论文被引用572次。显而易见,费恩曼不是一个高产的作者,他不信奉“不发表,就出局”的潜规则,所看重的是自己在解决问题过程中的那种愉快,而不介意别人是否捷足先登。费恩曼把他的一生都献给了物理学的研究和教育事业[1]。
1 费恩曼10大贡献
本节模仿朗道石碑,梳理费恩曼的一些主要成就。下文括号内的年份代表他正式在刊物上发表论文的时间,按照费恩曼本人认可的重要性,将成果从高往低排序。
1.1 费恩曼物理学讲义(1965年)
费恩曼认为他对物理学最重要的贡献不是量子电动力学,或超流理论,或极化子,或部分子,而是他的三卷《费恩曼物理学讲义》。这三卷书已译成10种不同的语言,并且还有4种双语版。该书起因于20世纪60年代,美国大学物理教学改革试图解决的一个主要问题是——基础物理教学如何尽可能反映近代物理的巨大成就。这三卷讲义中对许多问题的处理,反映了费恩曼自己以及其他在前沿研究领域工作的物理学家所惯常采用的分析方法。费恩曼在前言中写道[2]:“我讲授的主要目的,不是帮助你们应付考试,也不是帮助你们为工业和国防服务。我最希望做到的是,让你们欣赏这奇妙的世界以及物理学观察它的方法。”全书根据费恩曼课堂讲授的录音整理编辑而成,因而保留了费恩曼生动活泼、引人入胜、论述精辟、富于启发的独特风格。
1.2 弱相互作用理论 (1958年)
费恩曼受李政道和杨振宁于1956年发表的关于基本粒子弱相互作用中宇称不守恒的工作启发,与诺贝尔物理学奖获得者盖尔曼(M.Gellmann)合作,阐述了弱相互作用的“普适V-A理论”,这里V代表矢量,A代表轴矢量,他提出了“矢量流守恒”的假设,中子β衰变的矢量耦合常数与μ子衰变矢量耦合常数相等。费恩曼对他的这一成果非常得意,觉得“这是我第一次发现一条新的定律。”所以,本文把它列在第二位。
1.3 路径积分(1948年)
费恩曼在1947年春天对他的博士论文进行了整修,使之成为一种普遍性的理论。这篇发表在1948年《现代物理评论》上,题为“非相对论性量子力学的时间—空间方法”的总结性论文,第一次公开阐述他所创立的量子力学路径积分方法,即把从初始态到终末态的,所有在空间—时间中的可能路径所贡献的振幅,都叠加或者积分起来,以构成总振幅。当然,费恩曼实际上找到了建立量子力学的一种新方法,有别于海森伯(W.C.Heisenberg,1901—1976)1925年建立的“矩阵力学”和薛定谔(E.Schröding,1887—1961)1926年建立的“波动力学”,可为量子力学的第三种等价形式。
1.4 费恩曼图(1962年)
费恩曼发展了一种图形技术,能够大大地简化微扰计算的分析,这就是被普遍运用的“费恩曼图”。在这个图中,用顺时针时间方向的线段代表电子的运动,用逆时针方向的线段代表正电子,即电子的反粒子的运动。由于这是一种相对论性的理论,在图形中的每个节点的空时坐标,在计算中都要对整个空间时间积分。因此,在对由一个图形代表的那项的全部积分中,就包括了所有各个节点的时间先后次序各不相同的那些贡献。费恩曼图现在是所有量子场论进行微扰计算的工具,也就是它适用于所有的量子场论。
1.5 部分子模型(1968年)
早在20世纪60年代,费恩曼曾用直观图像来描述高能强子之间的相互作用,认为是通过强子内部的组成部分来完成的,他把这些组成部分称为部分子。1968年8月,费恩曼来到SLAC实验小组,人们向他展示电子与质子深度非弹性的反常结果,并告诉他用标度无关性作出的解释。费恩曼把质子看成是部分子(类点粒子)的复合体,把电子质子的深度非弹性散射看成是电子与部分子发生弹性散射。其实,费恩曼的部分子模型与盖尔曼的夸克模型异曲同工,他们从不同角度用不同方法达到了相同结论,原来部分子和夸克是一回事。
1.6 超流问题(1957年)
液态氦在温度2.19 K以下,会发生完全无阻尼的流动,这种现象称为超流。费恩曼从1953年到1957年期间研究超流问题。他认为以往的理论不够完整,因此用路径积分和量子统计的方法从头计算,定性预言了在低温下,系统会发生从常流体到超流体的相变。
1.7 量子引力理论(1962年)
费恩曼从20世纪60年代开始致力于将广义相对论与量子论结合起来,他坚信引力波的存在。他的工作一方面用关于引力的量子场论的方法重新给出了广义相对论的基本方程;另一方面则是进一步对微扰计算中所涉及的某些关键圈图的发散性质进行讨论,对量子引力问题做了基础性的工作。特别是在1962年,费恩曼首次用路径积分处理了引力理论中的规范不变性。
1.8 辐射的相互作用理论(1945年)
费恩曼为了消除经典电磁场理论中电子自能无限大的困难,试图取消电磁场,但又要反映电磁作用的有限传播速度(光速),这是一种在时间上的“推迟”。他使用一半推迟解,一半超前解,并且假定所有的作用源都被一种完全的吸收体环绕着,辐射阻尼就可以看作是由吸收体的电荷以超前波形式对作用源的一种反作用。在费恩曼的这种电磁学理论中,既不出现电磁场,也不出现电荷对自身的作用。这一工作的主要部分以费恩曼和惠勒联名的形式发表在1945年的《现代物理评论》杂志上。
1.9 曼哈顿计划(1945年)
费恩曼与理论物理学家贝特(H.A.Bethe,1906—2005)合作,在核武器的早期阶段,推导出适用于任何质量范围的爆炸效率公式,它一直被使用到现在,被称为“贝特—费恩曼公式”。
由图 7可知,随着 pH值的增大,HHCB和AHTN去除率的变化不大。总体上,当pH值处于2~6范围内,活性炭对HHCB和AHTN的去除率较高,在pH=6时,HHCB和AHTN的去除率最高分别可达95.96%和90.76%;当pH>6时,HHCB和AHTN的去除率均稍微下降。
1.10 学科和社会贡献(1945—1986年)
费恩曼对科学普及有着巨大的贡献,他著有4本重要的学术著作:《量子电动力学》《量子力学与路径积分》《光子强子相互作用》《统计力学》;编写了《物理定律的本性》《爱开玩笑的科学家》《你在乎别人怎么想?》《费恩曼讲物理》《费恩曼讲相对论》等科普著作。
特别值得提出的是,费恩曼在基础物理教育上的投入是无与伦比的。我们今天隆重纪念费恩曼先生,是因为他的科研与教学风格弥显珍贵,尤其体现在他知识丰富、正直幽默、热爱学生、有弄清任何问题秘密的迫切愿望,其中的第三点尤其令人赞赏,这有据可查,费恩曼对他的秘书海伦·塔克下了一个无条件的命令:“只要是想见我的学生,我都可以见。”无须讳言,费恩曼先生也有他的另外一个方面:过于表现、富有攻击性、缺乏尊重(有时让人不舒服)与合作。一些人会觉得费恩曼讲课具有狂热激情反而有点累人,繁琐而不够简明,有些东西是不言自明的,不必像他那样,绕一个大圈子来阐释。
2 费恩曼教学风格
费恩曼在加州理工学院(也就是那个如雷贯耳的并不改名为“大学”的MIT)的35年(1952—1987年)中,创下讲授过34门课程的纪录。特别是,他在1961—1962学年和1962—1963学年完整地为本科生开设课程,1964年又简略地重讲了一次,这次讲课的内容后来编成了《费恩曼物理学讲义》。
费恩曼为什么要花上两年多的时间改革基础物理的教学方法呢?大概的原因有3个:第一是他喜欢有一大群听众;第二个是他真诚地关爱学生;第三个可能是最重要的原因,按照他自己的理解重整物理学,并把他传授给年轻的学生,这是一项极富挑战性的工作。将艰深的概念化解为简单的、可以理解的词句,这种特色在三卷《费恩曼物理学讲义》中都很明显。
今天来看,费恩曼的教学方式也十分常规:全班180个学生每周两次聚集在一个大教室中听课,然后分成15~20个学生一组的复习讨论小组由助教进行辅导。此外,每周还有一次实验课。他在《费恩曼物理学讲义》[2]的序言中写道:“在这些课程中,我们想要解决的问题是,使那些充满热情而且相当聪明的中学毕业后进入加州理工学院的学生仍然保持他们的兴趣。他们早就听许多人说过物理学如何有趣,如何引人入胜—相对论、量子力学和其他近代概念。但是,当他们学完两年我们以前的那种课程后,许多人就泄气了,因为教给他们的是实际上很少有意义、重要的、新颖的和现代的观念。要他们学的还是斜面、静电及诸如此类的内容,两年过去了,不免令人相当失望。问题是,我们是否能开设一门课程来顾全那些更优秀、更勤奋的学生,使他们保持求知的热情。”
为此,费恩曼作出了以下的努力,同时指出严重的问题所在:
(1)针对班级中最聪明的学生,试图使所有的陈述尽可能准确,在每种场合都指出有关公式和概念在整个物理学中占什么地位,以及应该作出修正。
(3)在讲课的过程中遇到一个严重的困难:没有任何来自学生的反馈信息向我说明讲课的效果如何。
除了表演才能之外,他的教学技巧并不复杂。正如他给自己写下的一张便筏:“首先要搞清楚你为什么要学生学习这个专题,以及你要他们知道哪些东西,至于用什么方法就或多或少由常识给出了。”费恩曼所谓的“常识”就是完全抓住问题的本质。
费恩曼最反对的是“用字解释字”,即望文生意,因为这种简单的做法没有提供任何有用的信息;希望能跳出原来的命题,用生动的事例,用建立“思想实验”和类比的方法,借助于已知现象来解释新的现象。在费恩曼看来,这是数学物理学的伟大艺术。所以,他自豪地表白:科学真正的荣光在于我们能够找到一种思想方法,使得定律成为明显的。如果可能的话,赋予自然以某种机制,但又不至于预言其他实际不存在的现象。在你着手做实际的实验或大规模计算之前,不妨先考虑做一个“思想实验(ideal experiment)”,之所以要选它,是因为它易于想象。费恩曼将这种实验定义为:“就是所有的初始条件和最终条件都完全确定,没有我们无法计及的任何确定的外来影响的实验。”显然,这依赖于我们教师的知识储备和批判性思维能力[3]。
3 案例分析
笔者应清华大学出版社之约,出版25万字的拙作[4]。该书结合普通物理的有趣案例,设计了“追本溯源,道破天机;逻辑分析,想象助力;意料之外,情理之中;触类旁通、悟出真谛;他山之石,可以攻玉;学术争论,求实为先;思想之魂,启迪未来”等10章内容,还为《费恩曼物理学讲义》第一卷配备了100道问题及分析。
费恩曼谆谆告诫我们:“物理定律能够帮助人们认识和利用自然,但是我们还是应当不时停下来思考一下它们的真正含义是什么。”在目前我国的基础物理教材中,讲授的大多是表观唯象的知识,很少有像费恩曼那样刨根问底。例如费恩曼在他的《物理学讲义》第一卷中,专门开设了第12章“力的特性”。其中对大家耳熟能详的摩擦力(我们常讲静摩擦、滑动摩擦、滚动摩擦,而费恩曼将之分为干摩擦、湿摩擦)的机制进行了探讨。他写道:一种摩擦效应是重物同木板的相互作用,同其中原子的摇晃相关的一种非常复杂的效应。重物的有规则运动转化为木板中的原子的无规则的晃动,因此我们应当更进一步去观察。费恩曼的观点非常具有启发性,这比将摩擦归结为只不过是表面布满凹凸不平的形状,更深刻和可模型化。为此,本文开展随机关联势诱发的摩擦行为研究。
考虑一个质量为m的粒子处于一个施加偏压力F的破缺媒介之中,一方面粒子在运动过程中,受到正比于速度的湿摩擦力,另一方面还要翻越随机出现的许多小的势垒及势阱,这出现在蛋白质折叠的反应过程中。模型粒子的动力学方程如下
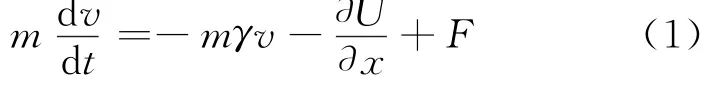
式中,方程右端第一项是通常的Stokes摩擦力,第二项的U称为随机关联势,它是一个随机函数遵守高斯分布,且系综平均满足:
方程(1)没有统一的解析解,为了对两种摩擦力效应进行比较,现考虑缺少和存在随机势两种情况。对于前一种情况,粒子速度为
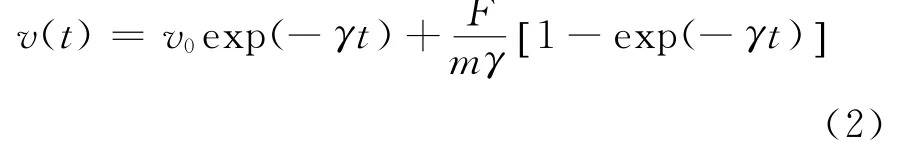
在长时间极限下,v(t→∞)=F/m()γ为一常量,粒子无加速度。若无线性偏压力(F=0),则粒子速度趋于零,这就是速度有关的湿摩擦力的常规作用。在第二种情况下,我们基于快速傅里叶变换(FFT)模拟产生随机关联势U(x)[5,6],然后数值求解方程(1),结果见图2。
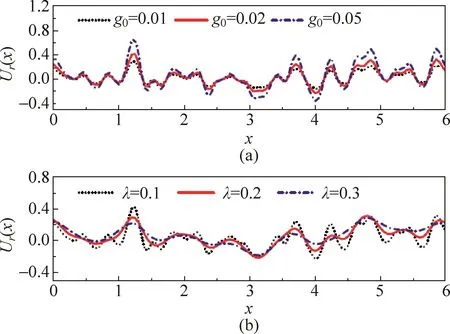
图1 用费恩曼猜测的分子随机运动来理解摩擦机制(a)λ=0.1;(b)g0=0.01
从图2中可见,当γ=0和F=0,随机关联势起到了等效摩擦及耗散动能的效果,即粒子从一定的初速度出发,最终将静止。不过,在γ=0和F≠0情况下,与湿摩擦相比较,当F取值较大时,结果发生了有趣的变化。倾斜外力对粒子做功,使其动能增加而足以克服随机势垒,因此粒子存在加速度。然而,当不存在随机势,粒子速度越大,其受到的湿摩擦力就越大,摩擦阻力-mγv将抵消外力F,粒子长时间后的速度等于一个常量而无加速度。
另外,费恩曼对摩擦力与速度之间关系的经验公式进行了独特的分析,他指出:“球、气泡或任意物体在蜂蜜那样的黏稠液体中缓慢运动时,作用于其上的摩擦阻力同速度成正比。但是当运动速度变快,以致引起液体打漩时(蜂蜜不会打漩,但水和空气会打漩),那么摩擦阻力就更接近于同速度的平方成正比F=-bv2,而如果速度继续增大,甚至这个定律也开始失效了。”以飞机为例,费恩曼不喜欢改变比例系数b,来分析空气阻力作用在机翼和机头上有什么不同。他说:“说得委婉一点,这是令人失望的,根据飞机形状来决定系数的简单定律是不存在的。”
费恩曼先生不愧是一位头脑清醒的物理学家,尽管刚才提到的事情的确是个问题,但不值得去研究,因为它太复杂了,给不出规律性的结论来。进一步思考后,我们是否获得了这样的启发:如果教师能够对物理学家的工作方式多少有一些了解的话,我们就不必担心当前的物理教育危机了,更不用发动一场让人啼笑皆非的将知识模块化、碎片化的“课堂战争”了。

图2 两种摩擦机制下粒子运动的比较(a)、(b)无外力,(c)、(d)有外力;(a)、(c)有不同γ而无随机势,(b)、(d)无γ而有随机势
一个有趣的问题是:与速度的多少幂次成正比的摩擦力形式,在关闭引擎情况下,直线运动的物体能在有限时间内停止?这里假设空气阻尼力与速度的某种幂成正比,即F=-bvnx,则初速度为v0的物体满足的牛顿第二定律为
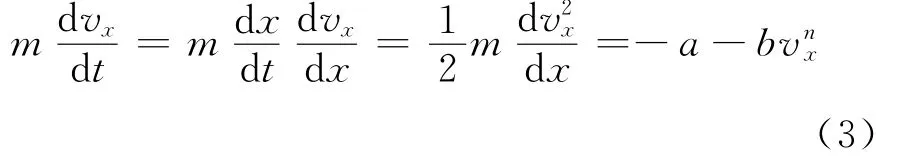
上式右边第一项代表与速度无关的干摩擦。若想要知道物体运动总时间与初速度的关系,则用以上方程的第一和第四项相等;而若计算物体移动的最长距离L与初速度的关系,则用第三项与第四项相等。经过定积分运算,它们分别是
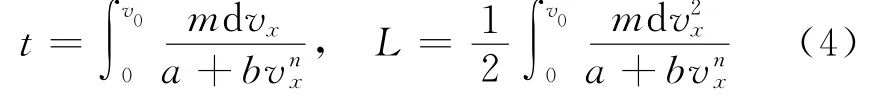
让我们研究与费恩曼考虑的高速运动相反的情况,即在低速情况下,物体所受到的空气阻尼与速度的关系又如何?这就像往空中投掷一个飞标,它在空中能飞行多长时间,直线运动的最大距离是多少?那么,可令a=0,典型的3种解答是
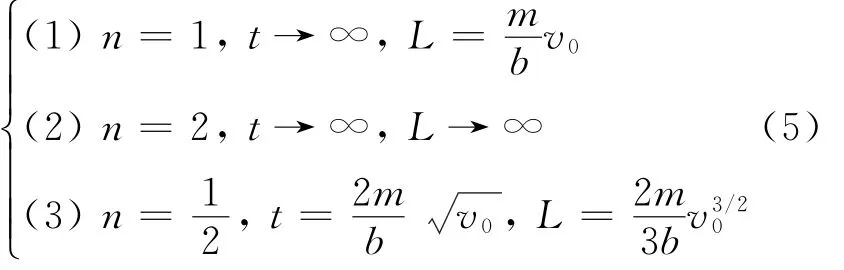
仔细分析这些结果是蛮有趣的。我们不去做定积分计算就可推知:若n>1,意味着速度越小,阻尼力也越弱,则t→∞和L→∞,这是不符合实际的;当n<1,阻尼力随速度的减小而变弱的程度要小,仍然起到阻碍物体运动的作用,所以物体可在有限的时间内停止运动。因此,从这个意义上来讲,物体在流体中所遭受的摩擦力与其速度成正比的假设,在低速情况下也需要修正。
4 结语
本文简单回顾了费恩曼先生的10个最重要的科学和教育成就,特别强调了费恩曼的教学技巧,即相关性、类比性、思想实验。本文第3部分以常见的摩擦这个力学问题为例,探讨了费恩曼所设想的分子随机扰动对物体运动的影响。独特的教学理念及教学技巧有利于保持学生学习的积极性和探索物理学发展的主动性,这也启示认课教师应该以生动的教学来激活学生的思维,使他们更靠近科学。

