Zakharov-Rubenchik方程的有界行波解及其精确表达式

胡丽金，刘小华

（1.黔东南州民族职业技术学院 公共教学部，贵州 凯里 556000；2.贵州民族大学 数据科学与信息工程学院，贵州 贵阳550025）

Zakharov-Rubenchik 方程［1］是研究等离子体的重要方程，也是物理和数学研究领域的重要内容。 F.Oliverira［2］证明了空间上一维Zakharov-Rubenchik方程的整体适定性，还证明了该方程孤立波解的存在性和轨道稳 定 性 。 F.Oliverira［3］、J.Cordero［4］、李 志 斌［5］和H.Nishiyama 等［6］分别在(0 ≤ k ≤ l+1 2)空间上研究了Zakharov-Rubenchik方程的全局适定性。到目前为止，关于该方程精确解方面的研究还较少。在本文中，我们利用平面动力系统理论分析了Zakharov-Rubenchik方程的有界行波解的存在性，并利用待定系数法和指数函数展开法导出了该方程的钟状解和扭状孤波解的精确表达式。

1　解的存在性

考虑以下Zakharov-Rubenchik方程：

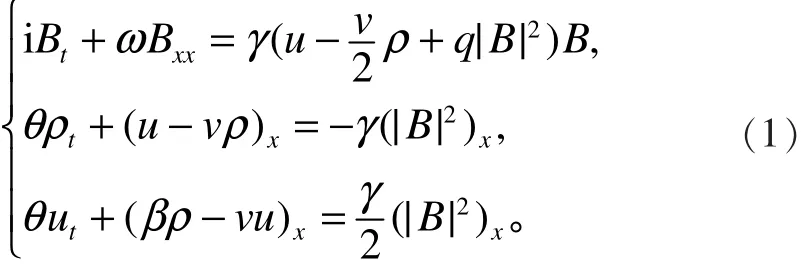
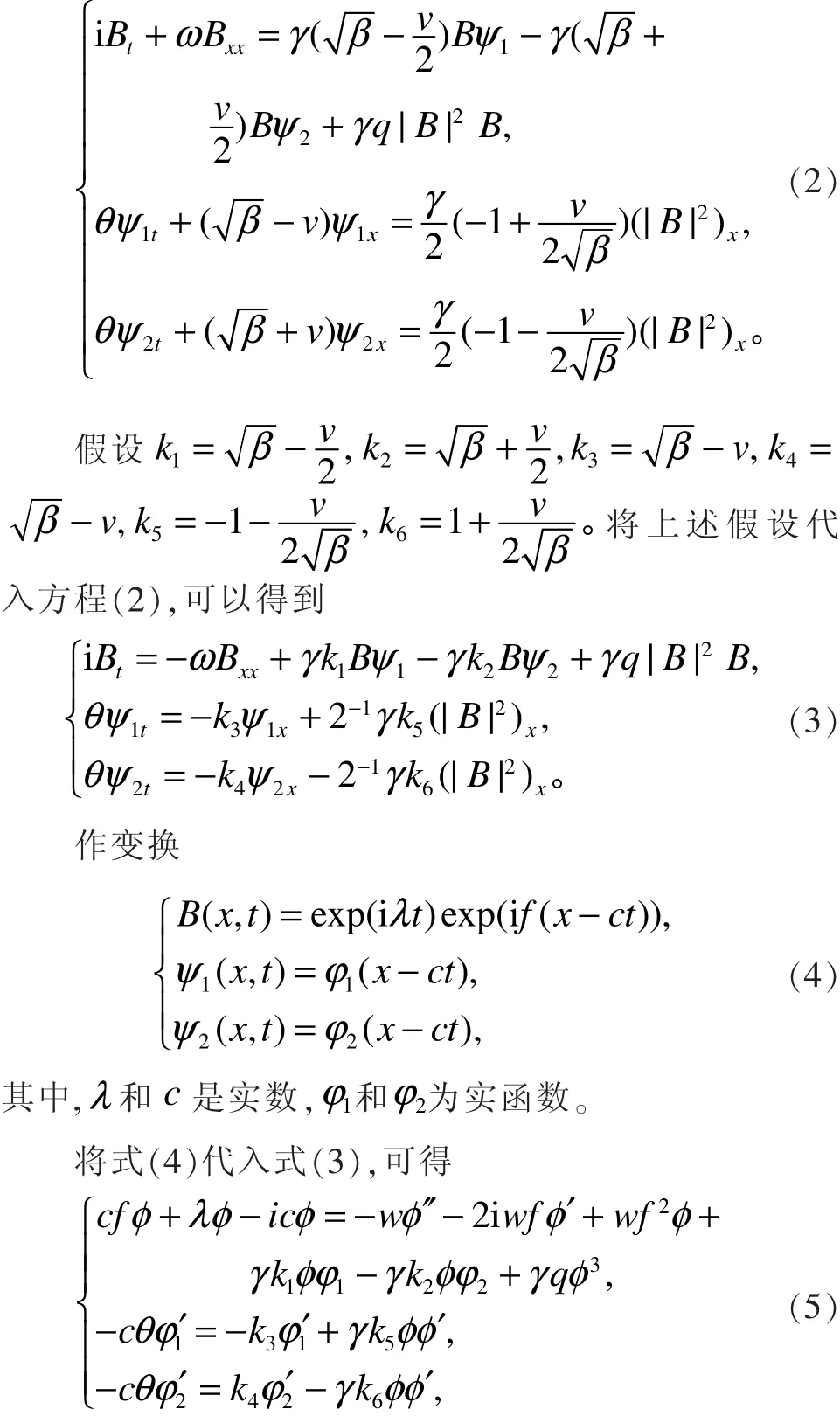
对方程（5）的第二式和第三式求不定积分，可以得到

将式（6）代入式（5）的第一式，令实部和虚部均为零,可得

下面借助平面动力系统理论分析系统（10）的相图轨线。

情形 1：当m( c2+4 w λ) < 0时，系统（10）有一个平衡点时，P为鞍点；而当1时，P为中心点。1

情形 2：当 m ( c2+4 w λ) > 0时，系统（10）存在平衡点 P1、P2和 P3，且当时，P为鞍点，1P2和P3为中心点；而当时，P为中心点，1P2和P3为鞍点。

因为系统（10）是一个保守的平面动力系统，所以系统（10）的势能函数为

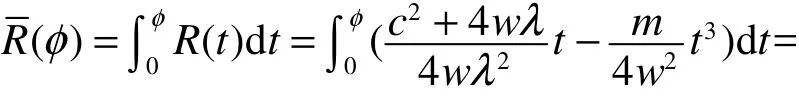
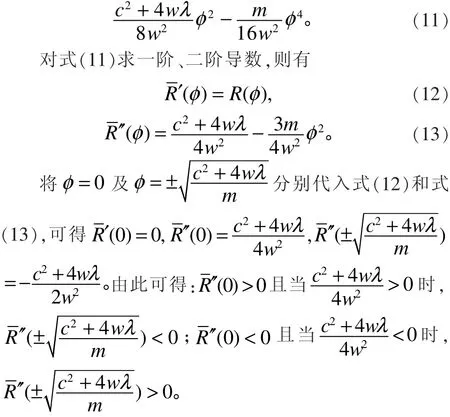
通过奇点分析可得系统（10）的相图（图1、图2）。

图1　时系统(10)的相图

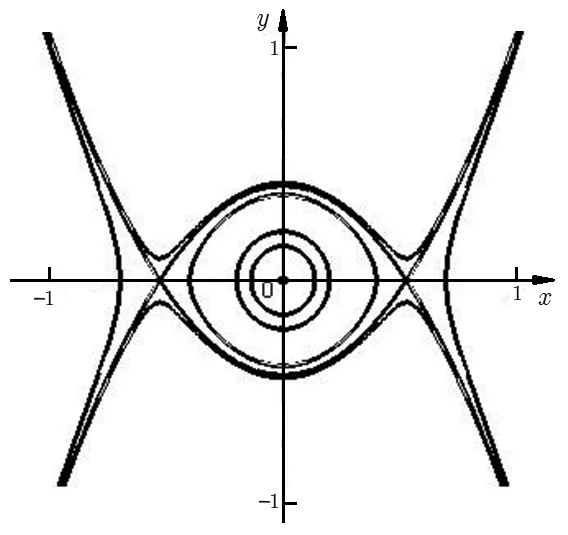
图2　时系统（10）的相图

从图1和图2可以看出，系统（10）同时存在两条同宿轨线和异宿轨线，系统（10）的同宿轨线对应方程（8）的钟状孤波解，异宿轨线对应方程（8）的扭状孤波解。

根据以上分析可得如下定理。

2　解的精确表达式

根据前面对方程（1）的定性分析，可假设方程（8）有如下形式

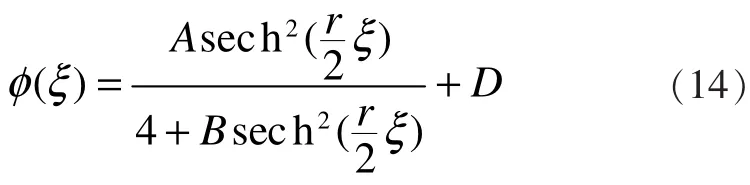
的解，其中A、B、D和r为待定系数。

对式（14）求一阶和二阶导数，可得

利用Maple软件求解方程组（15），可得

由式（4）、式（6）、式（7）、式（8）、式（14）和式（16）可得以下定理。

定理2：当λ、c、m和w 满足 c2+4 w λ<0和m<0时，方程（2）存在两个钟状孤波解，其表达式为

用类似的方法，假设方程（8）具有如下形式

的解，其中A、k和D为待定系数。

由式（14）可得

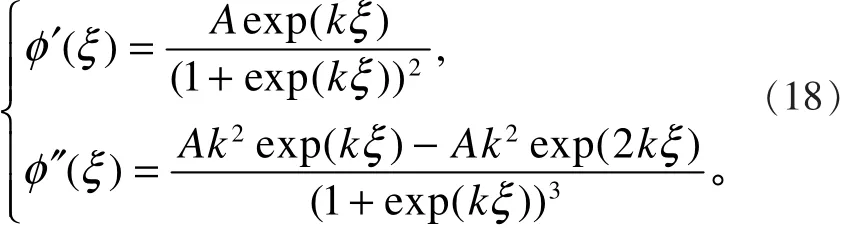
将式（17）和式（18）代入式（8），有

解方程组（19），可以得到

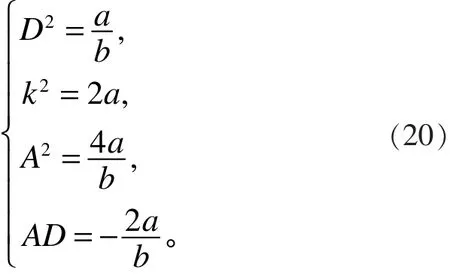
由式（20）可得：

根据以上计算结果，式（17）可以写成

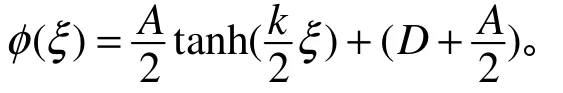
综合以上分析及计算结果，可以得到以下定理。

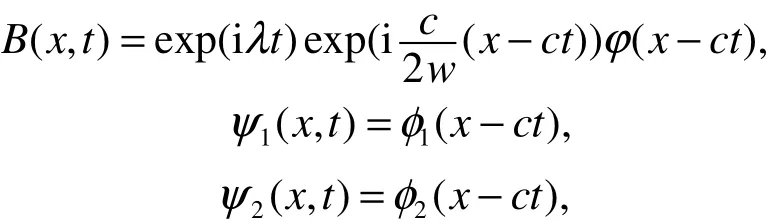
其中