空压机转子系统碰摩故障仿真分析*

吴　桃，常锡振

(1.常州铁道高等职业技术学校，江苏 常州　213011； 2.江苏天麒工业环境科技有限公司，江苏 常州　213000)

0　引　言

转子系统作为旋转机械的核心部件，常常出现各种单一或耦合的振动故障，研究这些故障对转子系统的影响，对及时发现并处理这些故障有着重要的意义[1]。以有限元和转子动力学相关理论为基础建立了转子系统的有限元动力学模型，并验证了模型的正确性，以此为基础对转子系统碰摩故障进行了分析。

1　转子系统的动力学模型

1.1　转子有限元模型建立

转子系统由一些离散的叶轮、具有分布质量及弹性的轴段和轴承座等部件组成，将系统离散成由刚性圆盘、轴段等单元连接成的模型，各个单元间在节点处联接，忽略转子系统的轴向变形[2]。弹性轴段单元的广义坐标分别为两端节点的位移的转角，如图1所示。

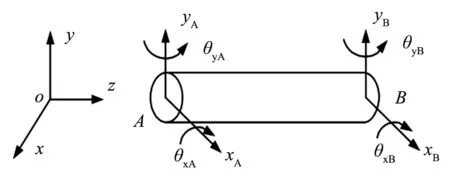
图1　轴段单元的有限元模型

其复数表示为：

μ=[xA-jyAθyA+jθxAxB-jyBθyB+jθxB

(1)

将多跨转子系统离散成具有N个节点、N-1个由刚性圆盘、弹性轴段和轴承支承的有限元动力学模型，其整体动力学方程为：

(2)

其中：M为整体质量矩阵；C=D+ωG；D为整体阻尼矩阵；G为陀螺力矩矩阵；ω为转子转速；K为整体刚度矩阵；矩阵为2N×2N阶对角方阵，具体形式参见文献[3]。

空压机轴模型如图2所示，将该转子系统离散成具有29个节点有限元动力学模型、其中共有28个弹性轴段单元，在叶盘和叶轮位置处，将叶盘和叶轮等效为刚性圆盘[4]，加在节点12～19、21、22处，轴承支承假设为等刚度弹性轴承，轴承刚度为k=108N/m，加载位置为9、10、22、23号节点。轴的材料密度为7 850 kg/m3，弹性模量为210 GPa,泊松比为0.3，阻尼比0.05。每个叶盘的质量为120.86 kg，极转动惯量为9.87 kg·m2，转动惯量为5.04 kg·m2，每个叶轮的质量为515.22 kg，极转动惯量为82.54 kg·m2，转动惯量为44.37 kg·m2。

同时用ANSYS进行模态分析，与直接建立的有限元模型求解结果进行对比，以验证模型的准确性。用ANSYS分析时选用beam188、mass21、combi214等单元[5]，并约束沿x方向的移动和翻转，其ANSYS有限元模型图3所示。

首先在Slid Works中建立转子系统的三维模型，包括主轴、叶盘、叶片，同时对各个部件赋予材料，借助于软件自带的模型评估工具，测量得到叶盘的转动惯量和叶轮的转动惯量并记录数值，记录各个轴段的关键点坐标，作为在ANSYS分析中的参数。

图2　空压机轴三维模型

图3　空压机轴有限元模型

1.2　模型验证及临界转速求解

对直接建立的有限元模型用MATLAB进行求解，提取了前四阶固有频率。所得空压机轴的前4阶固有频率如表1所示，其对比见图4。

图4　固有频率对比

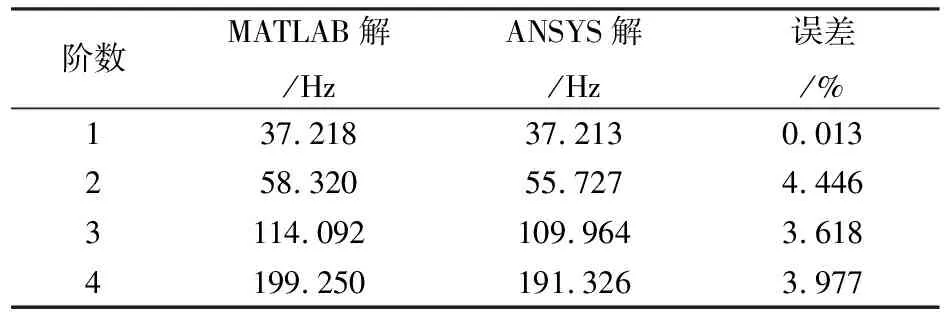
表1　固有频率

由表1及图4可知，对于前四阶固有频率，用MATLAB求解和用ANSYS求解的结果比较接近，误差不超过20%，因此在误差允许范围内，直接建立的有限元模型可用。

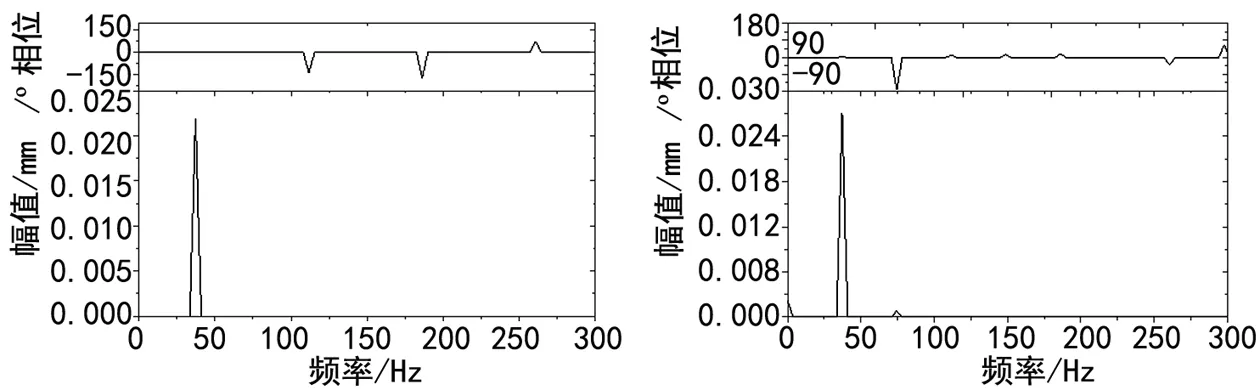
由公式(3)可求得该转子系统的一阶临界转速为2 233 r/min，二阶临界转速为3 499 r/min，三阶临界转速为6 846 r/min，空压机的额定转速为4 600 r/min，1.3n2

n=60f

(3)

2　转子系统碰摩故障分析

由直接建立的转子动力学模型可得到系统的质量、刚度、阻尼矩阵，并假设转子由于偏心质量的影响受到大小为104N的离心力，并作用在转轴中间的18号节点，如图5所示。转子在叶轮处发生碰撞，在21号节点加分段线性非线性碰撞力[6]如式(4)：

(7)

式中：间隙Δ=2 mm，非线性刚度k=108N/m。碰摩力如图6所示。图7和图8为21号节点X方向未加非线性碰撞的时域波形及频谱图，图8、10为21号节点X方向加非线性碰撞时的时域波形及频谱图。

图5　偏心质量引起的离心力　　　　图6　碰摩力

图7　无碰撞时时域波形　　　图8　碰撞时时域波形

图9　无碰撞时频谱图　　　图10　碰撞时性频谱图

通过对比无碰撞和有非线性碰撞的频谱图，无碰撞时未出现倍频等非线性现象，表现为线性的特点，对于有非线性碰撞的转子系统，频谱图中出现1、2等倍频，表现为强烈的非线性，说明碰撞对转子系统有较大的非线性影响。

当发生碰撞时，产生的2次谐波，其对应的转速约为4 466 r/min，因|n-2n1|<2n1·0.3，额定转速处于2次谐波的共振区内，因此在实际应用中，应尽量避免碰摩故障的发生。

3　结　论

(1) 通过MATLAB编程对转子系统固有频率的求解，并与ANSYS求解结果比较，验证了模型的正确性。

(2) 对转子系统进行了临界转速的求解，说明该转子系统为柔性转子，且运行时未处于共振区。

(3) 通过对空压机转子系统的碰摩故障分析，说明碰摩对转子系统有较大的非线性影响，在实际运行中应尽量避免碰摩故障的发生。