历史工单分析与智能派单的探索

刘海滨 中国铁塔股份有限公司响应中心工程师

1　引言

中国铁塔股份有限公司是3家电信企业联合出资成立的通信基础设施服务企业，目的是推动资源共享，减少重复建设，避免“双塔并立”、“多塔林立”等情形，并提升效率效益。公司主营通信铁塔、基站机房等配套设施及室内分布系统的建设、维护和运营，兼营基站设备的维护。

为及时、准确地掌握各机房等设施的状态，公司建立了完整的动环监控系统，能够及时掌握全国百万级站址及相关设备的情况。在有异常或故障时，能够及时告警并智能合并相关告警，生成工单，直接派发给一线的维护人员。一线维护人员通过终端APP可以及时接收工单并上站维护。

由于各站址地理位置、气候环境等都具有一定的特殊性和复杂性，某些工单的告警会自动清除，此时有些派单就浪费了一线维护人员的人力物力。因此，对工单进行研究分析，为进一步实施智能派单作出理论分析基础。

2　历史工单概览

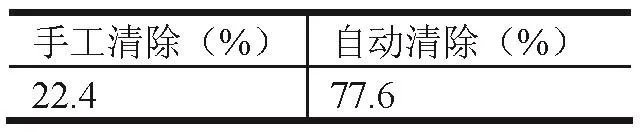
表1　历史完结工单

对历史完结工单进行分析统计，约有77.6%的工单告警会自动清除（见表1）；未上站维护且自动清除的工单占总工单的比例约为65.4%（见表2）。因此，不需上站且自动清除的工单是本次分析的重点。

表2　未上站维护且自动清除的工单

智能派单的目的是减少一线维护人员无效上站的次数，对发出的工单确实需要维护人员上站维护。那么智能派单的基础就是工单不需要人员上站维护而且告警会自动消除，通过上述分析可知，这一部分占到了样本工单的65.4%，具有相当大的分析价值和操作空间，本文分析所指的工单告警就是这一部分。

通过分析样本数据，告警自动消除且未上站的工单中排名前20位的工单告警类型如表3所示。

从表3可以看出，排名第1的“交流输入停电告警”占工单告警问题中的36.31%，而第20名告警只占告警总量的0.22%。前20名告警的累积比占告警总量的98.24%，即在所有告警中98.24%都在这20个告警中。因此，本文主要分析前20名告警，且排列顺序均按此表中的次序排列。

3　分析思路

首先判断一个工单的告警是否会自动消除，如果告警不能自动消除，就只能派单，让一线维护人员上站检修。如预测的告警会自动消除，如何决策何时派发该告警生成的工单给一线维护人员，既能保证站址维护的质量，又可最大化地避免一线维护人员的空跑，高效利用人力资源，节约成本。因此，智能派单分为两步，一是预测该告警产生的工单是否会自动消除；二是统计分析该告警消除的时间分布情况，来决定何种告警何时派单效果较好。

表3　前20位工单告警类型

4　KNN算法测试

分析告警是否会自动清除，采用的是机器学习中的KNN（k-NearestNeighbor）方法，即K近邻法。

K最近邻（KNN，k-NearestNeighbor）算法是机器学习中十大算法之一。所谓K最近邻，就是K个最近的邻居的意思，即每个样本都可以用它最接近的K个邻居来代表。

KNN算法的核心思想是：如果一个样本在特征空间中有K个最相邻的样本中的大多数属于某一个类别，则判定该样本也属于这个类别，并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分类样本所属的类别。KNN方法在类别决策时，只与极少量的相邻样本有关。KNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别，因此对于类域交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合。

KNN方法的核心思想如图1所示。图1中，问号处圆点要被决定赋予哪个类，是属于三角形还是四方形？KNN的思想是以问号处的圆点为圆心，画等距离线（如实线圆圈与虚线圆圈），如果K=3，由于三角形所占比例为2/3，圆点将被赋予三角形类；如果K=5，由于四方形比例为3/5，因此圆点被赋予四方形类。

以告警清除方式作为被预测值，预测告警是否会自动消除，本次试验中经过测试K=7时预测的效果最好。训练时，对不同告警赋予了不同的权重值，权重值为各告警在样本中出现的次数，并且将是否上站作为一个输入项，通过对样本集的训练，KNN对测试集的预测效果如表4所示。

说明如下：

data_test_label是测试集标签，即在测试集中已知每个样本是属于哪个类的，以行为代表，0代表告警为手工清除，1代表告警为自动清除，即行的数据代表实际情况。

data_test_pred是通过KNN方法对测试集作预测分类，0表示预测告警为手工清除，1表示预测告警为自动清除，以列为代表。

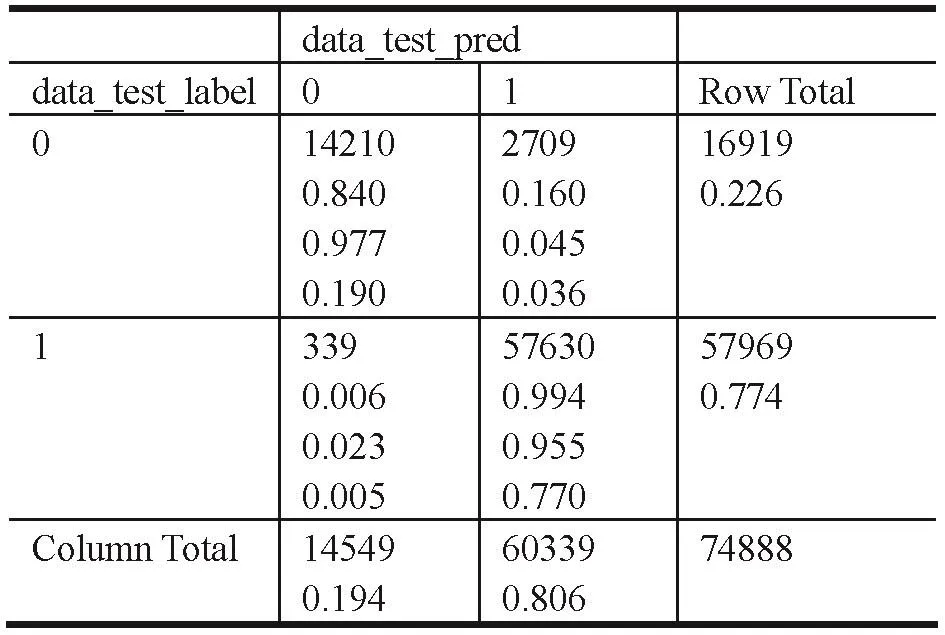
表4　KNN对测试集的预测效果

Row Total代表本行有多少数据，即测试样本中实际为0或1的有多少数据。

ColumnTotal代表本列有多少数据，即测试样本中预测为0或1的有多少数据。

具体说明举例如下：

测试样本中为0的数据实际有16919行（即0与Row Total列组合处），通过KNN测试为0的数据为14210行（即0，0组合外，表示预测正确），通过KNN预测为1的数据为2709行（即0，1组合处，表示预测错误）。

测试样本中为1的数据实际有57969行（即1与Row Total列组合处），通过KNN测试为0的数据为339行（即1，0组合处，表示预测错误），通过KNN预测为测试样本中1的数据为57630行（即1，1组合处，表示预测正确）。

以三行三列位置处（1，1组合处）具体说明，测试样本中实际为1的样本数为57969行（即1与Row Total列交集），其中预测为1（即预测正确）的数据有57630行（即1，1组合处），正确率为0.994（57630/57969），错误（1，0组合处）率为0.006（339/57969）。预测为1的数据一共有60339行（Column Total行与1组合处），预测正确的有57630行（1，1组合），预测正确率为0.955（57630/60339）。预测为1实际也为1的数据有57630行，占测试总样本（Column Total行与Row Total列组合处）中的0.770（57630/74888），测试总样本为74888行（Column Total行与Row Total列组合处）。其他数据同理。

测试样本中，实际为0、1的比例分别是0.226（16919/74888，0与 Row Total列组合处）与 0.774（57969/74888，1与Row Total列组合处）；预测结果中，预测为0、1的比例分别为0.194（14549/74888，Column Total行与 0组合处）与 0.806（60339/74888，Column Total行与1组合处）。

由表4可知，当预测一个工单的告警会自动消除时，准确率为95.5%（即1，1组合处），即预测一个告警会自动消除，95.5%是真的会自动消除的，4.5%的概率是不会自动消除的，即预测错误的概率为4.5%。

5　工单时间分布

根据对历史工单告警恢复时间的分析，工单告警为自动消除且不需要上站的前10名累计占92.46%，前20名累计占98.24%，覆盖了绝大多部分情况，因此关于告警恢复时间的分析，均是针对工单告警会自动消除且不需要上站的情况（即表3中的数据），前20名告警分布时间如图2所示。

图2中纵坐标是告警名称，按告警占比例排序，从下到上，占比依次由大到小，可见横作标是告警消除需要的时间（持续时间），此图标示出不同种类的告警在告警自动消除所需时间上的大概分布情况。通过告警种类与持续时间的对比（颜色的浓密代表了数据是否密集），不同告警持续的时间不同，离异点的情况也不同，但总体可以看出，大部分都会小于500min。

如图3所示，每种告警数据分布不同，每种告警对应行的着色从左到右由深到浅，表示数据分布由集中到分散，具体数据的集中分布程度的展示，需要通过箱线图（见图4）。

如从0～12的自然数中，13个数从小到大排列，最小的是0，对应图5中下角线（表示最小值，即下部分虚线最下的横线），最大的是12，对应图4中的上角线（表示最大值，即上部分虚线最上的横线）。

四分位数（Quartile），即统计学中，把所有数值由小到大排列并分成四等份，处于三个分割点位置的数值就是四分位数。

第一四分位数（Q1），又称“较小四分位数”，等于该样本中所有数值由小到大排列后第25%的数字，对应图表3中柱体的下边线，在本例中是3。

第二四分位数（Q2），又称“中位数”，等于该样本中所有数值由小到大排列后第50%的数字，对应图表3中柱体的中线，在本例中是6。

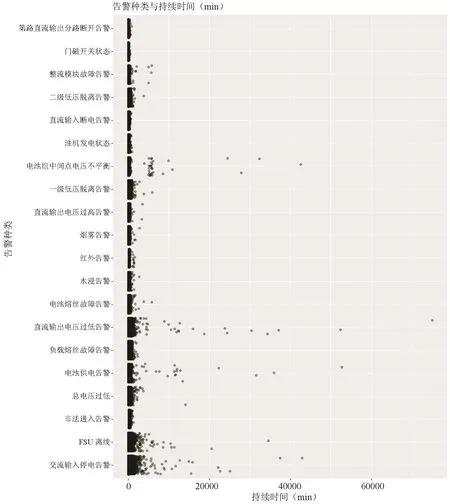
图2　前20名告警分布时间

第三四分位数（Q3），又称“较大四分位数”，等于该样本中所有数值由小到大排列后第75%的数字，对应图表1中柱体的上边线，在本例中是9。

第三四分位数与第一四分位数的差距又称四分位距（InterQuartileRange，IQR），对应图表1中的整个柱体，在本例中是6。

图4的箱线图是垂直显示，图5是横向显示，箱线图含义相同。

箱线图用于展示数据分布情况，示例中数据是均匀分布，所以图形看起来是对称的，但实际中数据千差万别，如某些数据比较集中，第一四分位数可能与第二四分位数重合等情况发生。

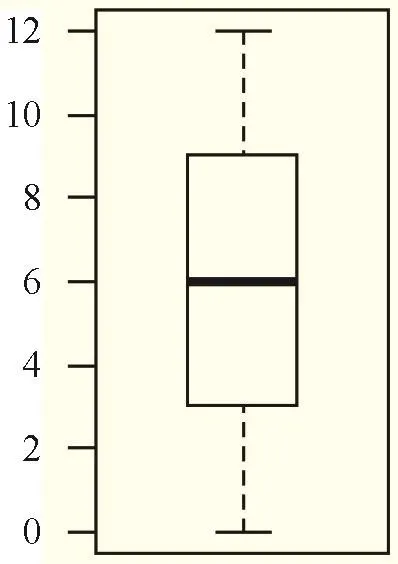
图4　箱线图（垂直显示）

图6是图3的箱线图展示，进一步说明各种告警在不需要上站维护时自动恢复所需要的时间分布情况。

以“交流输入停电告警”为例，25%的数据是在15min以下，50%的数据约是在47min以下。而“非法进入告警”的第一四分位数、第二四分位数及第三四分位数间差距比较小，75%的数据约是65min以下。具体数据参见表5。

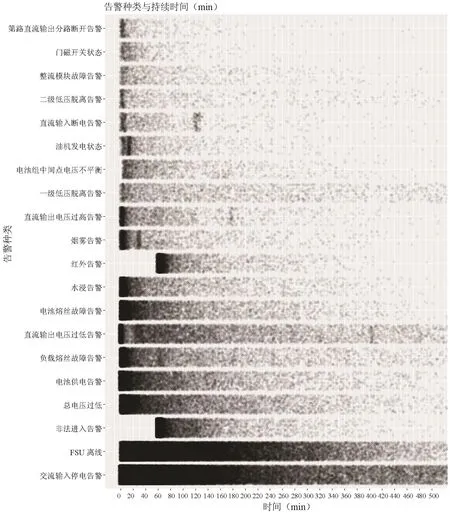
图3　500min以下告警种类和时间

图5　箱线图（横向显示）

6　结束语

通过KNN算法预测分析一个告警是否会自动清除，在一定情况下可考虑延迟派单，根据图6和表5所示，延迟一定时间在相应的概率下工单的告警会自动清除，如“交流输入停电告警”，延迟15min，有25%的概率告警会自动消除；如延迟47min，有50%的概率告警会自动消除。

系统目前每日产生12万左右的工单，65.4%会自动消除且不需要上站操作。如果将某些告警产生的派单作一定的延时，可减少许多派单量，如排名第一的“交流输入停电告警”，占比为36.31%，如果延时派单15min约可减少25%的工单量，即减少的工单量约为7124（120000×0.654×0.3631×0.25）条；上站维护的工单量占工单总量的13.4%，如果按照这个比例进行推算（假定上站维护的工单量与工单问题保持一定的线性关系），减少的7124条工单会间接减少954（7124×0.134）次上站，以每次上站维护成本200元计算，只此一项每天就可节省成本约19.08万元。

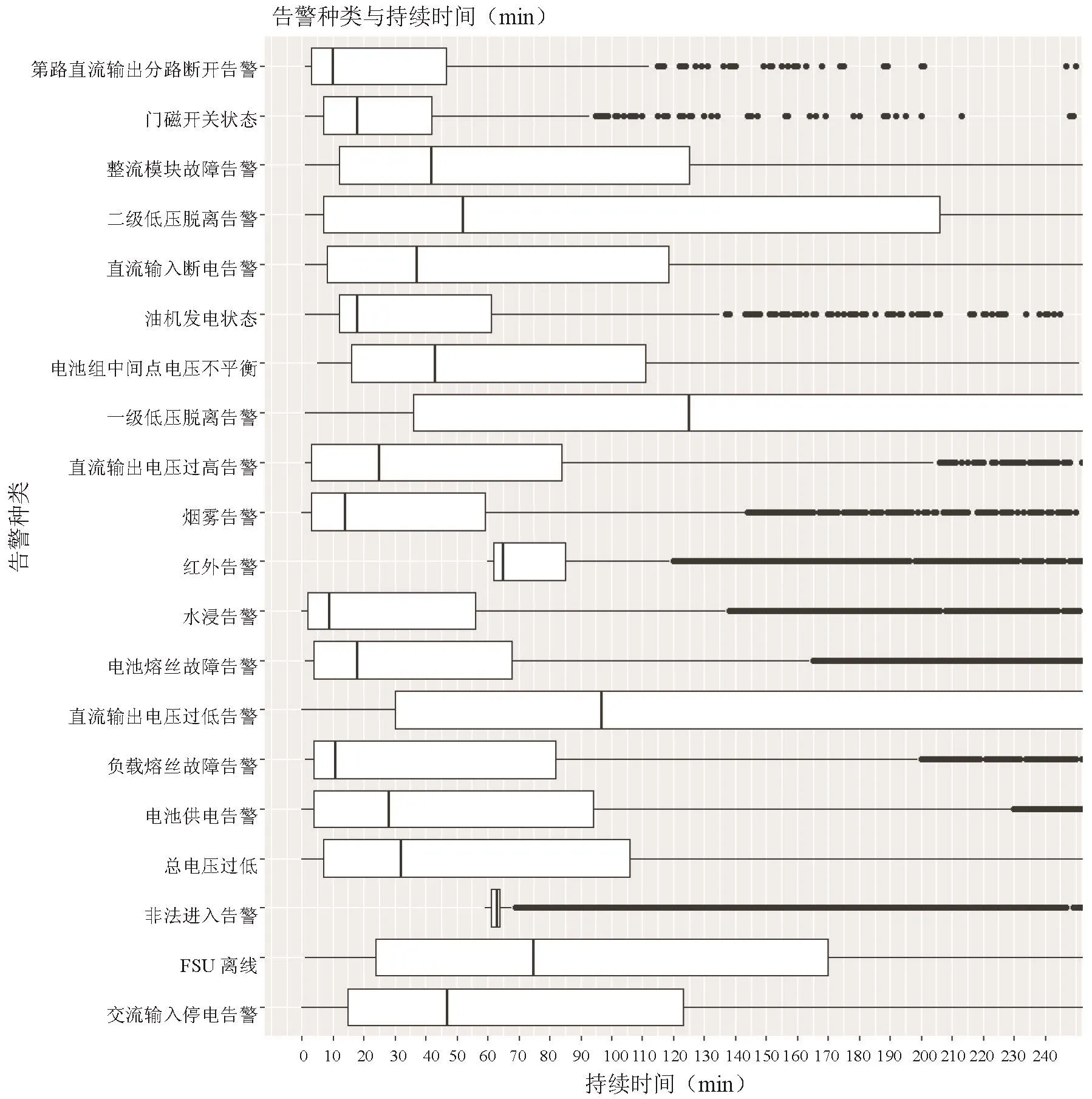
图6　图3箱线图展示

对同一个站址的告警已实现基于规则的智能合并，大大减少了重复告警及无效告警的产生。在告警产生后，基于何种标准及状况需要一线维护人员上站进行检修维护，根据行业特点和实际情况决定。

目前，分析的方法与结论还有一些局限性：数据是抽样获取，没有覆盖一个完整的生命周期，如果想更准确，需要大数据分析，获得多个生命周期的数据。此次分析只是针对本公司该问题解决方案的一个大致画像及探索方向，包括对特征值的提取、算法的选择及参数优化等。

离异点比较多，说明数据分布不成正态分布，第一四分位数可能不足25%的比例。

目前，只能预测告警是否会自动消除，至于告警产生的具体原因及消除原因并不清楚，需要调研分析。

以上分析只是对智能派单实现思路的一种尝试，在告警恢复的时间分布分析中，可以进一步细分，如加入时间、地域、设备品牌、天汽等因素，结合告警产生的原因等因素，这样可以作到更精细、更准确的分析评估。在决定是否需要派单以及何时派单时，更加的客观全面，更加合理有效地利用一线工作人员的人力资源，作到精确、高效维护，不断提高维护保障的质量与效率。

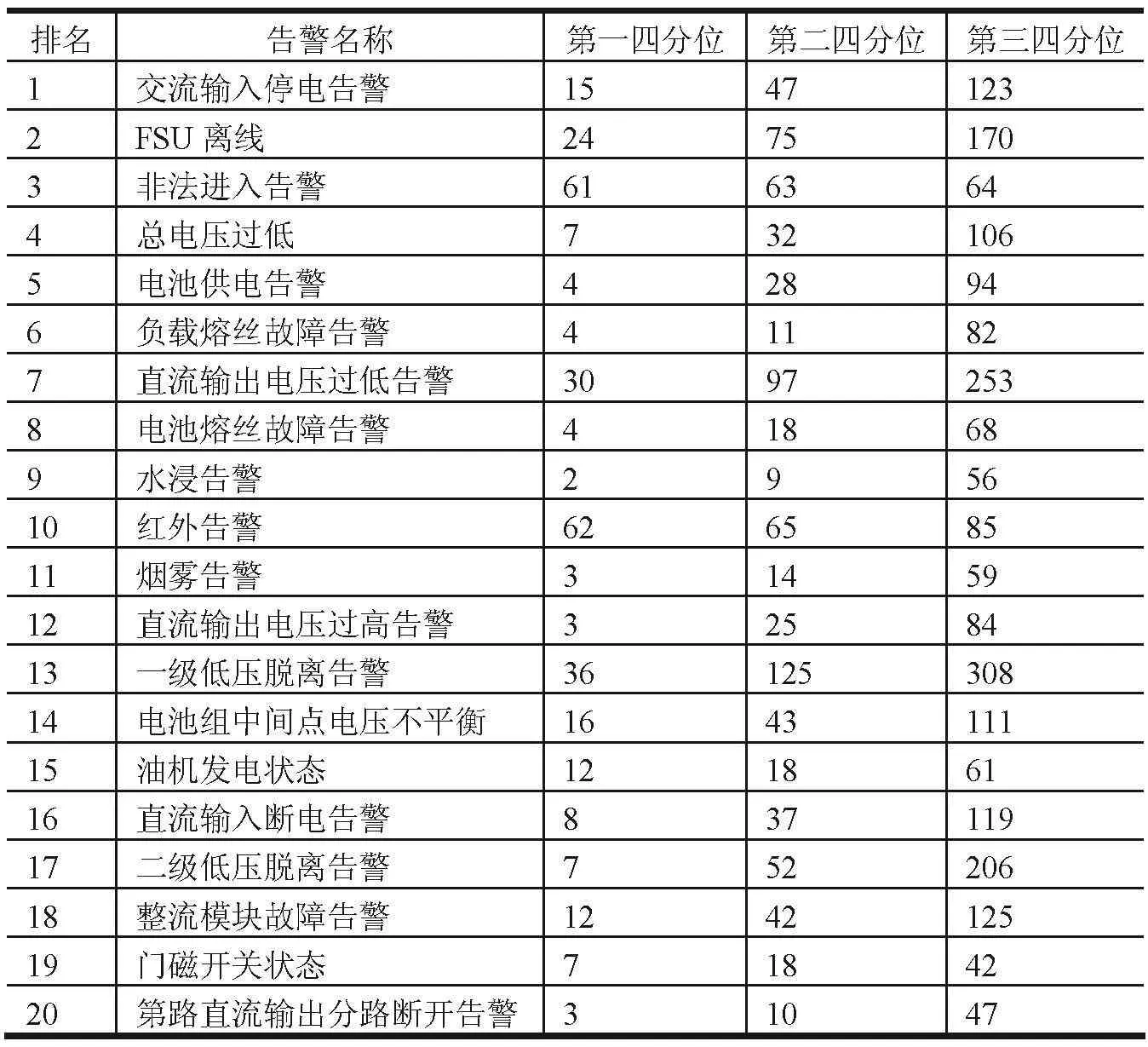
表5　工单时间分布