不同咀嚼功能下全瓷固定桥牙弓曲率的三维有限元研究*

陆晓丰，凌厉，董宁，董海东，袁秀祥

（1.南京医科大学附属无锡市精神卫生中心 口腔科，江苏 无锡 214063；2.江苏省无锡瑟维思通自动化设备有限公司，江苏 无锡 214063）

口腔牙弓形态大致表现为尖圆、椭圆形、方圆形[1]，不同的牙弓形态导致牙列曲率存在较大的差异性。牙弓尖牙前后是弓形较为弯曲、曲率变化较大的区域，在行使切割、撕裂和研磨食物等不同咀嚼功能时各牙受力大小和方向也有差异，故此处牙齿缺失后采用全瓷固定桥修复其修复体本身受力情况存在着复杂性。本实验通过研究不同咀嚼功能、不同曲率牙弓形态下全瓷固定桥应力情况，探讨载荷大小一致情况下载荷角度、固定桥牙弓曲率对固定桥应力数值及分布的影响，为临床全瓷固定桥桥体设计以及全瓷材料的选择提供生物力学性能方面的参考。

1 材料与方法

1.1 材料

1.1.1 数字模型 本实验采用的是课题研究建立的数字模型，该模型是以左上尖牙缺失后左上侧切牙、左上第一双尖牙为基牙的单层全瓷固定桥模型。

1.1.2 实验软硬件 台式电脑（CPU：Core i5-7500，内存：DDR4 2400MHz8G，显卡：Nvidia GeForce GTX 1050）；Solid Works 2014软件（DassaultSystemes公司，法国）。

1.2 方法

1.2.1 数字研究模型的建立 本实验的数字模型是通过使用Micro-CT对离体牙进行断层扫描后经逆向工程软件重建的、符合临床实际的全瓷固定桥数字模型，本模型包括了全瓷桥、牙釉质、牙本质、牙髓、牙周膜和牙槽骨等实体部件，大致可分为固位体就位预备后牙体的组合体2个（左上侧切牙、左上第一双尖牙各1）、桥体1个（左上双尖牙牙冠部分）、支持结构1个（牙周膜和牙槽骨部分）以及连接体。全瓷桥固位体是边缘线为基牙牙釉质颈缘边线、颈部为厚度1 mm的90°肩台、轴面厚度1.5 mm、咬牙合面厚度2 mm的全瓷冠[2]；桥体为尖牙牙颈部弧形切断后形成的单结构全瓷桥体；连接体截面大小为3 mm×2 mm[3]。由于牙弓曲率大小不一，本实验以侧切牙及第一双尖牙的近远中向的辅助轴线的交角为变量设计4大组实验模型（见图1），分别0°（A1组，直线型）、30°（A2组）、60°（A3组）、90°（A4组、垂直型）。固定桥内3个单元建立各自的辅助坐标系，确保在牙弓曲率不同的情况下都能按照牙齿三维空间参数排列[1]。牙槽骨实体是由下底为12 mm、上底为17 mm、高为15 mm的等边梯形的截面在釉牙骨质界根方2 mm处沿着固定桥近远中辅助轴线的连线为线条曲线扫描而来，其长度为30 mm；牙周膜实体是在基牙牙根根面偏移0.25 mm形成，高度同牙槽骨下底平面。

1.2.2 有限元分析设置材料属性 模型各部件材料均假设为连续、均质、各向同性的线弹性材料，各材料具体力学参数见表1[4-5]。①设置约束条件：各部件为固定接触，周围牙槽骨为刚性边界。②设置载荷条件：侧切牙、尖牙受力方向为与牙齿长轴成45°角，受力位置为牙体舌侧切1/3与中1/3交界处宽度为1 mm、至边缘嵴的狭长区域，面加载100 N；第一双尖牙受力方向为与牙齿长轴平行、垂直于牙合面，位置为中央窝直径4 mm的圆形区域，面加载100 N[1]。上述各牙相对于该牙受力方向不变是通过建立该牙辅助坐标系来确保这一条件得以实现。每组模型内侧切牙、尖牙、第一双尖牙单独施加载荷，分为1、2、3共3个类别（例如A1组侧切牙受力模型组命名为A1～1）。

1.2.3 有限元应力分析指标 第一主应力（σ1，最大峰值记为σ1max）：根据第一强度理论，脆性材料通常以断裂形式失效，该数值反映某一点的最大拉应力。等效应力（Von Mises应力，最大峰值记为Von Misesmax）：是第一、第二、第三主应力的计算值，反映了某一点综合受力情况。

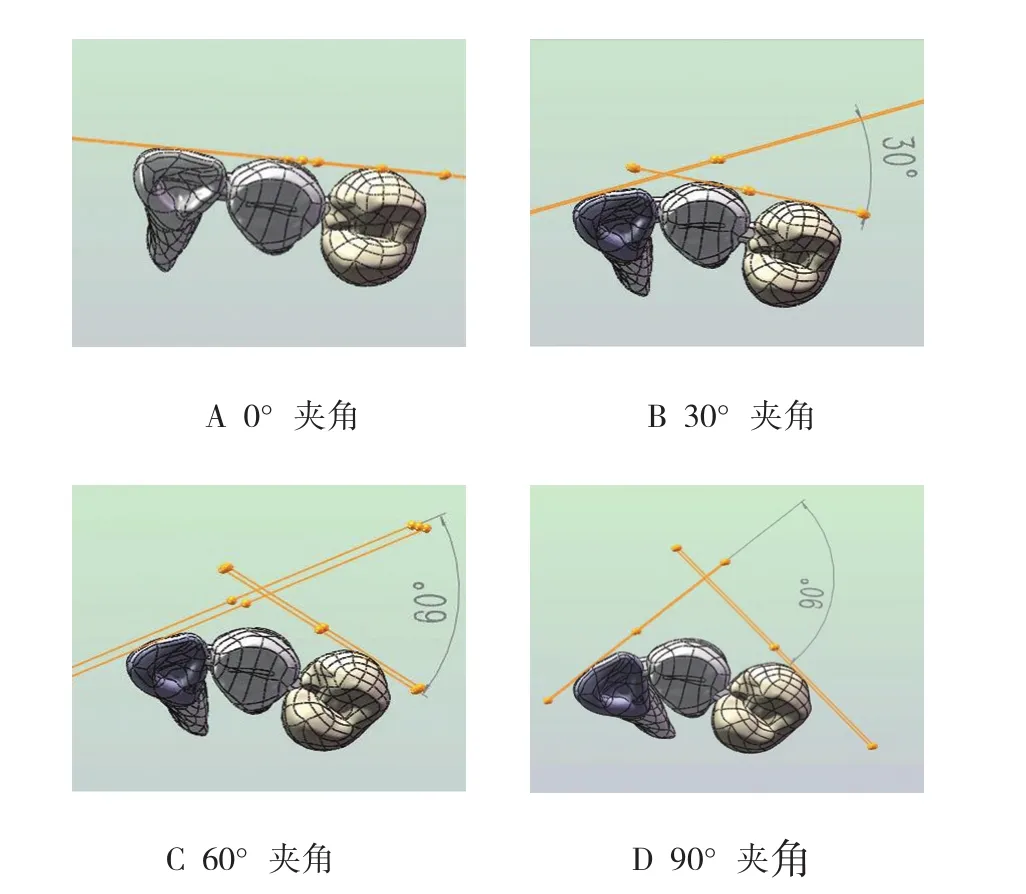
图1 辅助线交角

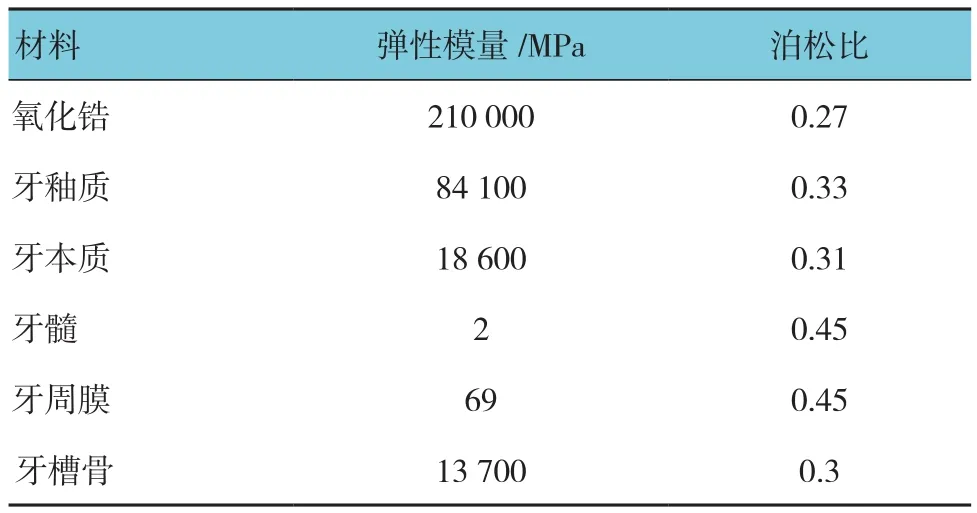
表1 模型材料的力学参数

2 结果

在组间，随着固定桥牙弓曲率的增加，固定桥的σ1max以及Von Misesmax随之也增加（见表2）；侧切牙、双尖牙施加载荷时，应力主要集中连接体部位；第一双尖牙施加载荷时，应力主要集中该牙的牙合面受力区部位（见图2）。在类别组内，施加载荷大小相同的情况下，侧切牙组所表现的应力极值大于第一双尖牙组，且随牙弓曲率增大而增大的趋势比第一双尖牙组大（见图3）。

表2 全瓷固定桥应力值

图2 A1模型组固定桥应力数值及分布情况

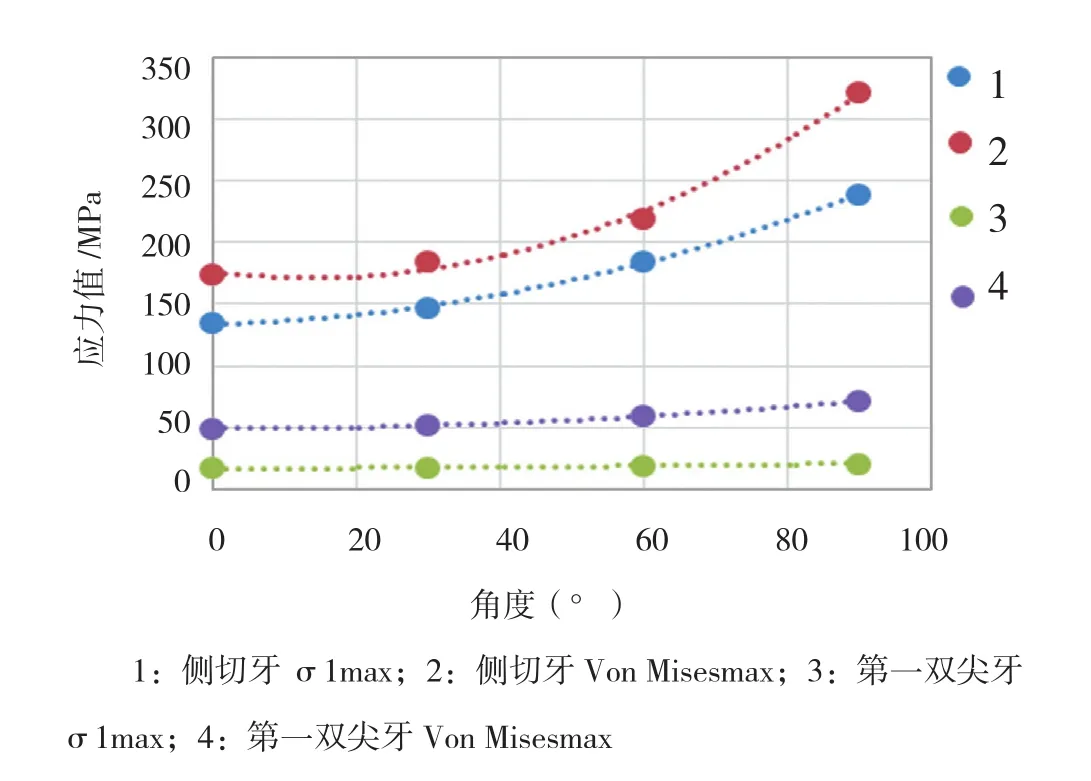
图3 应力与角度（曲率）关系趋势图

3 讨论

全瓷固定桥是修复牙齿缺失的常用方法之一，由于其具有良好的生物相容性、极高的美学特性等优点已在口腔修复中广泛应用[6-7]。由于尖牙前后是牙弓曲率变化较大的区域，故本实验所采用的模型是以左上尖牙缺失后左上侧切牙、左上第一双尖牙为基牙的单层全瓷固定桥模型。由于固定桥桥体组织面与牙槽嵴黏膜为无压接触[2]，为避免在有限元分析中产生力的传导而干扰应力结果，本模型中精简了牙龈组织；由于均匀的粘结层厚度对修复体的生物力学性能影响轻微[8]，而且不影响应力分布及应力传导[9-10]，按照有限元分析法简化模型的假说，本模型中精简了粘结剂层。正常人左上侧切牙、左上尖牙、左上第一双尖牙男女平均咬牙合力分别为100、175和200 N[1]，且在咀嚼过程中这3个牙齿所发挥功能不同，施力角度也不一致，本实验为对比相同咬牙合力情况下不同咬牙合角度位置、不同牙弓曲率对固定桥应力的影响情况，统一施加载荷为100 N。

尖牙由于其牙根粗壮，在口腔内使用寿命相对较长，但也存在着由于龋齿、外伤或先天缺失等各种原因导致的尖牙缺失。由于对缺牙区牙槽骨骨量、手术接受因素及容貌美观等多因素的考量各不相同，临床上有部分患者在严控适应证的前提下可采用全瓷固定桥的修复方式。目前对全瓷桥固定修复体的有限元力学研究主要集中在前牙或后牙固定桥，此类固定桥的牙弓较为平直，而且同一桥体上的受力方面较为一致和单一[11-12]。尖牙前后牙齿缺失采用固定桥修复时，修复体包括前后牙，前后牙在行使咀嚼功能时所发挥的功能不同，且该区域由于牙弓形态的不同其曲率变化大小不一，该两方面因素对修复体力学表现情况影响的研究鲜见，也是本实验研究的重点。

全瓷固定桥作为一种美学修复体，经临床使用验证是可靠的缺牙修复方式。有学者回顾99个3或4单位氧化锆固定桥修复体7年后临床使用情况，总存留率为83.4%，支架发生断裂的情况在失败病例中占8%[13]。修复体的力学表现是其临床使用寿命的基础。有学者用三维有限元法研究不同支持形式（天然牙、种植牙、天然牙和种植牙联合）的全瓷固定桥的力学表现，发现不同的支持形式表现出类似的应力分布情况，最大应力也都集中在连接体的龈方[14]。由于全瓷固定桥的连接体是应力集中的区域，该处最容易发生支架断裂现象[15]。

本实验数据显示，组内前牙、后牙承受相同载荷时显示差异明显的应力极值以及不同的应力分布形式。双尖牙受力时表现的应力极值小于侧切牙组类别及尖牙类别组，应力集中于该牙的牙合面受力区部位，与有些学者研究后牙单冠垂直受力情况相类似[16-17]，主要是因为垂直施加在双尖牙固位体上的载荷表现实质主要是一种压力而不是拉力，而且这种垂直向压力由于基牙的存在容易传导至牙槽骨而不易扩散转移至邻近结构。尖牙（桥体）受力时，其侧向施加的载荷表现出一部分拉力，而且该牙两侧都存在固位体可以传导应力，表现为较为均衡的受力状态[18]，所以应力极值介于其他两个类别组之间；相对于侧切牙，第一双尖牙与该牙存在由于牙弓曲率带来的更大的施力角度差可能是导致应力极值出现在尖牙和双尖牙之间的连接体上的原因，这和有些学者研究不同材料的固定桥应力集中于连接体部位的结论是一致的[19]。侧切牙受力时，相较于尖牙，侧切牙的斜向载荷在牙合平面上的分力更多的表现为一种拉力，曲率越大，这种相对于双尖牙近远中方向上的拉力越大，具体体现在固定桥内部应力的极值也增加[20-21]，高于尖牙、第一双尖牙。有学者研究后牙固定桥载荷角度对修复体应力的影响，认为斜向加载对固定桥框架的断裂有着重要影响[16]。本实验结果提示，固定桥在承受相同咀嚼力，行使切割、撕裂或研磨食物等不同功能时，不同的受力角度位置对修复体应力情况有着重要的影响：载荷位置越远离第一双尖牙，固定桥应力值越大；垂直施加负载时固定桥应力小，承载能力高，载荷角度越是斜向，固定桥应力越大，承载能力低。

在本实验中，侧切牙、尖牙、第一双尖牙单独受力时固定桥应力极值（包括第一主应力和等效应力）随着牙弓曲率的增加随之增加。尤其是第一双尖牙类别组（A1-3、A2-3、A3-3、A4-3），该类别组不仅承受的载荷大小和区域相等，而且载荷施加角度也一致（在绝对坐标系中的角度恒定），区别仅仅是固定桥牙弓曲率有差异，其应力结果显示应力极值是随着牙弓曲率增加而增加的，表明固定桥牙弓曲率是影响应力情况的重要因素。从表2的实验数据中选取4大组侧切牙、第一双尖牙单元体受力时第一主应力和等效应力数值而建立的“应力与角度（曲率）关系趋势图”（见图3）显示，随着固定桥牙弓曲率的增加，侧切牙组应力极值增加的趋势明显比第一双尖牙组大，这表明牙弓曲率以及由于曲率增加而导致被改变的载荷方向（绝对坐标）这两者对于应力的影响存在叠加放大效应。与一些学者建立的平直牙弓固定桥的应力极值相比[19-21]，本实验采用载荷为100 N的单个牙位负载受力情况下表现出来的全瓷固定桥的应力极值反而明显增大，提示固定桥牙弓曲率是影响固定桥应力表现的重要因素，固定桥牙弓曲率越大，固定桥应力值越大。

本实验通过三维有限元法阐明不同牙弓曲率的全瓷固定桥修复体在行使不同咀嚼功能时其修复体力学性能的基本情况。研究结果提示笔者在临床上采用高曲率牙弓全瓷固定桥修复体时，由于高应力的出现，应采用挠曲强度较高的全瓷材料来避免材料本身挠曲强度不足而导致桥体破裂情况的可能；同时也提示大家在连接体设计时尽可能采用优化设计避免局部应力过度集中导致材料疲劳出现连接体断裂的情况。

本实验仅建立单层全瓷桥，简化对饰瓷的研究；选择静态加载的受力方式，简化牙合运循环的复杂性，与口腔修复体实际使用情况尚存在一定的差异性，有待进一步深入研究。全瓷固定桥的设计涉及方方面面的因素[22-23]，尤其是上颌尖牙前后牙齿缺失采用固定桥修复时，固定桥跨越前后牙区，除了要考虑牙合力大小和方向、修复体自身曲率等因素所带来的生物力学上的不同表现，还要参考基牙牙周储备力因素，更要兼顾桥体设计与义齿外形之间的美学问题[24-25]，只有综合考量，才能设计出美观耐用的全瓷固定桥。