某型电子设备连接铆钉断裂分析

肖　滨，常选仓，关　迪，刘　杰

(中国电子科技集团公司第二十九研究所，　四川 成都 610036)

引　言

当前，电子设备正朝向微系统化、一体化方向发展，但设备的环境条件却变得越来越苛刻，这直接导致相关结构的强度裕度不断降低，结构失效风险越来越大。对机载设备而言，飞机在起降、飞行、机动过程中会遇到大量的随机振动和冲击载荷，如何在满足结构功能性要求的前提下保证结构强度安全，就成为结构设计中亟需解决的课题。文献[1]利用有限元软件对某电子设备进行了瞬态动力学仿真，分析了连接铆钉在冲击载荷下断裂的具体原因并提出了改进建议；文献[2-3]分别研究了铝板在随机振动载荷下的疲劳特性和金属材料的低周疲劳损伤演化模型；文献[4-6]分别对具体结构在随机振动载荷作用下的响应进行了试验或仿真分析，为利用有限元计算进行结构随机动力学仿真提供了思路和方法。但上述工作都是在载荷条件已知的前提下进行的，一些实际使用中发生的结构破坏的载荷条件往往不明确或难以确定，此时上文中的方法就不再适用，只能寻求其他手段来对结构的失效原因进行判断、验证。

某电子设备在装机飞行一段时间后出现了大范围的铆钉断裂现象，在无法获得外部载荷的情况下，本文通过断面特征反推了载荷条件，并对铆钉失效过程进行了仿真计算，重点从静强度、疲劳强度等方面对比说明了铆钉断裂的原因。

1　问题描述

图1为某型机载电子设备支撑结构的实物及安装示意。图1(a)圆盘中部是不锈钢自制螺母，通过4个自制铆钉铆接在圆盘上。使用时先将2个图1(a)所示圆盘分别通过螺钉安装在设备的上下内表面，然后用一个长度为80 mm的不锈钢自制螺杆从设备上表面自上而下穿过第一个自制螺母，再从第二个自制螺母的反向旋入，通过该自制螺杆对设备上下表面起到固定支撑作用。

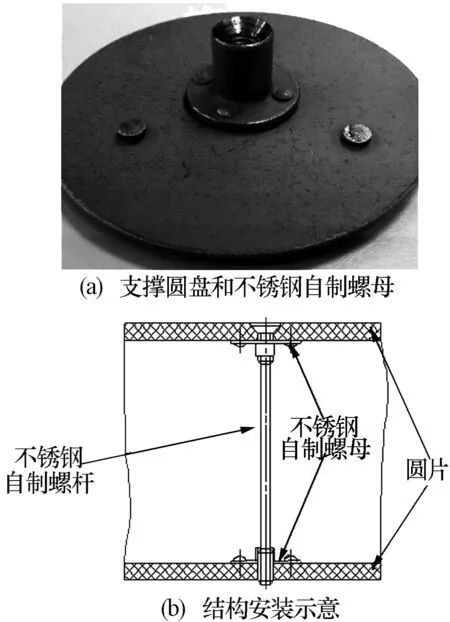
图1　某设备支撑结构实物及安装示意

实际使用中发现，该结构安装比较困难，并且连接自制螺母和圆盘的4个铆钉出现了大量破坏现象，结构破坏后的照片如图2所示。

图2　破坏后的圆盘与自制螺母

分析后认为，该设计至少存在两个问题：1)上、下圆盘的自制螺母孔中心很难对准，这导致自制螺杆在反向旋入下表面的自制螺母时偏心，这一点从图2(a)中心处螺纹孔的磨损情况也可得到证实，偏心会让铆钉在安装后承受较大的剪力作用。2)无法保证上、下圆盘上自制螺母的距离恰好就是其螺距的整数倍，这会导致安装完成后上、下圆盘不可避免地承受沿其表面法线方向的拉载荷，载荷传递到铆钉上就表现为沿铆钉轴向对铆钉的拉力作用。由此可知，铆钉在整个支撑结构安装完成后需承受轴向的拉应力和横截面内剪切应力的双重作用，本文将基于此进行仿真分析，给出导致铆钉断裂的真正原因。

2　仿真分析

2.1　有限元建模及边界条件设置

在保证外形尺寸、对外接口、连接关系与真实结构相同的前提下，考虑支撑结构的上下对称关系，只对上表面的圆盘、自制螺母、铆钉及连接上下表面的螺杆进行建模，由Catia V5完成包含所有结构细节的全尺寸三维建模，由Abaqus和Fesafe软件完成仿真计算。采用适应性较好的六面体单元C3D8R对模型进行网格划分，其中网格总量为73 937个，节点数为92 147个。完整的有限元模型如图3所示。

图3　有限元计算模型

根据该支撑结构对外的真实连接形式，在圆盘的4个对外安装孔孔边固支以模拟外部结构对圆盘的位移约束，同时采用“面-面接触”来定义螺杆与螺母之间、螺母与圆盘之间、铆钉与螺母和圆盘之间的接触关系，在螺杆的下端面施加位移条件以模拟实际安装中的偏心和拉/压载荷作用。螺杆和自制螺母材料为不锈钢1Cr18Ni9Ti，铆钉材料为L4，圆盘材料为铝合金LY12。

2.2　有限元计算

由于缺乏明确的位移/载荷输入，在此需先对圆盘所处的安装环境做必要分析，以确定仿真计算所需的位移/载荷条件。通过观察图2(a)中螺纹孔磨损区域中心与孔中心线的距离，确定螺杆中心线与螺纹孔中心线偏移量最大约为0.9 mm；通过分别测量上、下圆盘在自然状态下和螺杆拧紧状态下的间距，确定螺杆拧紧后上、下圆盘间距缩减量为0.7 mm。以此作为图3模型中螺杆端面的位移条件进行仿真分析，计算结果示意如图4～图6所示。

图4　支撑结构整体变形

图5　支撑结构的Mises等效应力分布

图6　连接铆钉的Mises等效应力分布

各零件的最大计算Mises等效应力Smax见表1。其中：σy为材料屈服强度；σb为强度极限。

表1　各零件的最大计算Mises等效应力

由表1中计算结果可知，螺杆与螺母的最大Mises等效应力均低于其屈服强度，并有较大的安全裕量；圆盘和铆钉局部的最大Mises等效应力均已超过其屈服强度，但并未达到强度极限；说明整个支撑结构在安装完成后局部已经产生塑性变形，但并未发生破坏，因此可以排除结构静强度破坏的可能。

考虑到该设备的安装环境是机载平台，在使用中不可避免地会受到来自载机的振动载荷作用，因此不能排除装配应力和来自载机的振动载荷共同作用导致铆钉疲劳破坏的可能。同时根据图2(a)中螺纹孔的磨损情况及载荷与位移的对应关系可知，该设备在实际使用中螺杆中心线与螺纹孔中心线的偏移量最大不会超过0.9 mm，因此其所承受的最大应力幅值也不会超过Smax。按最严重情况计算，假定Smax就是设备各零件在实际使用中承受的最大应力幅值，将上述有限元计算的结果文件导入Fesafe软件，对整个模型进行疲劳寿命计算，以对该设备铆钉断裂的原因做出进一步分析，计算结果示意如图7～图8所示。

图7　结构整体对数疲劳寿命

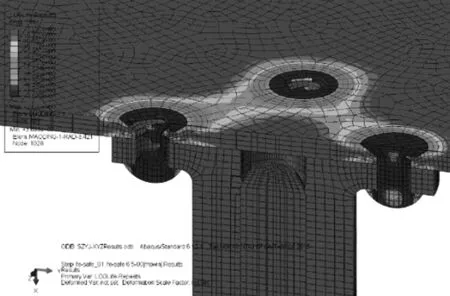
图8　铆钉完全断裂对应的疲劳寿命(5 489次循环)

对比图7、图8和图2(b)可以看出，疲劳计算得到的铆钉疲劳断裂过程及最终断裂位置和真实情况高度一致，铆钉都是在圆盘与自制螺母接触面处断裂，说明仿真计算较好地还原了铆钉断裂过程。此外根据表1结果可知，装配应力单独作用不可能导致结构失效，因此结合断面和上述分析结果可知，铆钉断裂的主要原因就是较大装配应力和来自载机的振动载荷共同作用下的疲劳破坏。从上述计算结果也可很直观地看出，连接圆盘与螺母的铆钉是整个结构失效的危险细节，在当前载荷下其疲劳裂纹出现对应的疲劳寿命仅为2 228次循环，至完全断裂的疲劳寿命也仅为5 489次循环。假定整个结构工作时所承受的载荷频率为1 Hz，这意味着铆钉在承载37 min后即开始产生疲劳裂纹，在大约1.5 h后就会完全疲劳失效。

3　结束语

在缺乏明确载荷输入的前提下，本文利用断面特征定量反推了结构上、下表面的相对位移量，并据此对整个结构进行了仿真计算，准确预测了该设备连接铆钉的断裂位置，还原了铆钉疲劳断裂过程并给出了铆钉的疲劳寿命，计算结果对结构优化改进有较强的指导意义。

一般来说，装配应力不会对结构安全造成太大影响，但文中情况是一次典型的过大装配应力与来自载机的振动载荷叠加引起的结构破坏现象。在装配精度无法通过加工保证的类似结构设计中，适当增加柔性部件，同时提高不同金属部件之间的刚度匹配度，可适当补偿装配应力对结构安全造成的不良影响。

结构的安全寿命往往取决于其结构最危险细节的疲劳寿命，但在最危险结构细节得到优化或加强后，之前的次危险结构细节会上升为最危险结构细节(比如文中结构中的圆盘安装孔边，对应疲劳寿命为14 859次循环)，成为影响结构安全的最关键因素，这在结构设计改进和优化时需引起重视。

参考文献

[1]刘杰, 关迪, 肖滨, 等. 某电子设备铆钉冲击断裂原因分析与改进[J]. 电子机械工程, 2017, 33(4): 26-30.

[2]HU H T, LI Y L, SUO T, et al. Fatigue behavior of aluminum stiffened plate subjected to random vibration loading[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(5): 1331-1336.

[3]关迪, 孙秦, 杨锋平. 一个修正的金属材料低周疲劳损伤模型[J]. 固体力学学报, 2013, 34(6): 571-578.

[4]陈文华, 崔杰, 潘骏, 等. 航天电连接器振动可靠性试验与分析[J]. 航空学报, 2003, 24(4): 342-345.

[5]张军, 谌勇, 张志谊, 等. 卫星随机试验的振动响应分析[J]. 机械强度, 2006, 28(1): 16-19.

[6]孟凡涛, 胡愉愉. 基于频域法的随机振动载荷下飞机结构疲劳分析[J]. 南京航空航天大学学报, 2012, 44(1): 32-36.