客运专线纵断面线形重构的思路与方法

杨嘉岳， 周　锬， 杨文昕

(西南交通大学土木工程学院， 四川成都 610031)

客运专线具有高平顺性、高稳定性的特点，但是在多年的运营和维护后，客运专线的线路难免会发生偏移，线路的平顺性受到影响，在线路的平面曲线地段和纵断面竖曲线地段，轨道的几何形位和线形的改变相对于直线地段尤为明显，目前针对平面线形的重构已经取得了较多的成果[1-3]，提出了根据曲率、斜率、方位角等参数的变化对平面线形进行分段，结合迭代拟合[4]的思想，实现了平面线形的重构，在纵断面线形的重构中，拟根据相同的思路，首先对纵断面线形的里程和高程数据进行测设，在得到满足测设精度要求的各项数据后，对纵断面测设数据进行粗略分段和精确分段，在此基础上，根据纵断面起落道量在直线地段为点位到拟合直线的距离，在曲线地段为点位到拟合的竖圆曲线圆心的距离与半径的差值，进行纵断面起落道量的计算，恢复纵断面线形的平顺性，以满足客运专线的平顺、安全和舒适。

1　里程与高程数据的测设

客运专线对线路的平顺性要求相对于普速铁路更高，意味着对测设点位的里程数据与高程数据提出了更高的精度要求，随着现代测量技术的发展，在客运专线中线的测量中，已经有比较多的成熟的测量技术，通过全站仪和轨检小车系统，在轨道控制网的基础上，对客运专线线路中线的里程与高程数据以及对应里程处左右钢轨的高程数据进行测量，得到众多高精度的线路中线、左右钢轨里程与高程数据。

客运专线对平顺性的要求比普速铁路更高，需要测量得到的里程数据与高程数据尽可能全面地体现纵断面的实际位置，因此测设数据点位之间的里程间隔应该足够小，相邻测点的间隔可以考虑取为一个轨枕间距0.625 m，在高精度高密度的线路中线、左右钢轨里程与高程测量数据的基础上，展开客运专线纵断面线形重构的探讨，为恢复客运专线在纵断面上的平顺性提供一定的参考。

2　纵断面线形分段

在进行纵断面线形重构前，汲取平面线形重构的经验[5]，首先需要根据纵断面线形的特点，对纵断面线形进行分段，鉴于基准钢轨纵断面线形不受超高的影响，故纵断面线形的重构拟针对基准轨展开。在基准轨纵断面线形中，最明显的特征即是相邻直线坡段坡度发生改变，故可以根据坡度的变化对基准轨纵断面线形进行粗略分段。

在粗略分段完成的基础上，为了提高线形重构的准确性，需要提高线形分段的精确程度，故在粗略分段的基础上，展开线形的精确分段。

在平面线形的精确分段中，迭代拟合的思想应用广泛，在平面线形的精确分段中取得了很好的效果，线形分段的精确程度达到了一个轨枕间距0.625 m以内。在纵断面线形的精确分段中，拟采用同样的思路，实现纵断面线形的精确分段。

2.1　粗略分段

粗略分段即根据测设点位信息，对其归属做出大致判断，不要求达到非常高的精度，只需粗略分段结果能满足后续的线形拟合即可。粗略分段流程如图1所示。

图1　粗略分段流程

粗略分段步骤：

(1)根据实测里程与高程数据计算一定间隔的测点位置的坡度大小；

(2)绘制坡度图，并根据坡度变化规律确定直线坡段的近似坡度大小与分段点位置的近似里程，主要依据为：由上一直线坡段过渡到下一直线坡段的过程中，坡度发生明显的变化，在直线坡段，坡度理论上为定值，由于线形可能发生改变，故直线坡段的坡度将在某一定值附近波动，故可根据此变化规律确定坡度近似值与分段点近似里程位置。

2.2　精确分段

精确分段需对测设数据的归属尽可能地做出准确的判断，直至最终确定的分段点里程不再影响数据的分段结果，即连续两次确定的分段点的里程差值不超过限值，限值可根据实际需求确定，精确分段流程如图2所示。

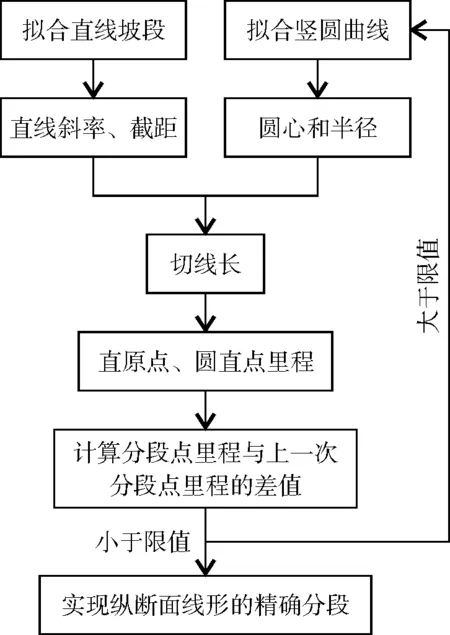
图2　精确分段流程

精确分段步骤：

(1)在粗略分段的基础上，将测设点位数据分为竖圆曲线段和两侧相切直线坡段三种区段，对各自坡段内的测点数据分别进行线形的拟合，通过拟合得到竖圆曲线圆心位置、竖圆曲线半径以及竖圆曲线两侧直线坡段的斜率和截距；

(2)在拟合结果的基础上，根据直线坡段拟合结果，计算变坡点里程位置与坡度代数差；

(3)根据竖圆曲线拟合结果，计算竖圆曲线切线长，以此确定分段点里程位置；

(4)根据分段点里程位置，对测设点位数据重新进行分段，并参与到各自对应线形的拟合中去，当连续两次得到的分段点里程差值不超过确定的限值时，即认为纵断面线形的分段达到了精确分段的效果。

3　纵断面线形拟合

在纵断面线形分段中，将涉及到到直线线形与圆曲线的拟合问题，需采用不同的模型分别进行拟合计算。

3.1　拟合模型

直线线形的拟合模型为：

Y=kX+b

式中：k为直线斜率；b为直线截距。

竖圆曲线的拟合模型为：

(X-XO)2+(Y-YO)2=R2

式中：XO为竖圆曲线圆心O的里程；YO为竖圆曲线圆心O的高程。

拟合问题中，需要找到使得误差达到最小的直线和竖圆曲线的线形表达式，常用的衡量标准为偏差的平方和达到最小：

式中：ri为任意点位的偏差。

3.2　拟合方法

在曲线的拟合中，常用的拟合方法[6]主要有以下三种。

3.2.1最小二乘法

最小二乘法基于最小二乘原理，认为点位的横坐标或者纵坐标存在但并不同时存在偏差，并使得偏差的平方和最小，下面以直线的拟合来说明。

当横坐标作为自变量时，基于最小二乘法的偏差如图3所示。

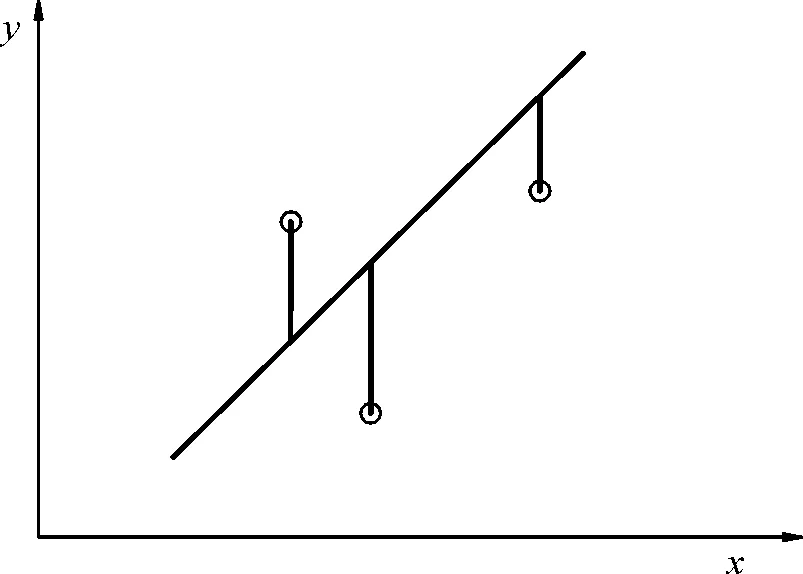
图3　最小二乘法沿Y轴方向的偏差

当纵坐标作为自变量时，基于最小二乘法的偏差如图4所示。

图4　最小二乘法沿X轴方向的偏差

3.2.2基于距离最短的最小二乘法

在最小二乘法的基础上，将偏差视作点到直线的最短距离，则基于距离最短的最小二乘法的偏差如图5所示。

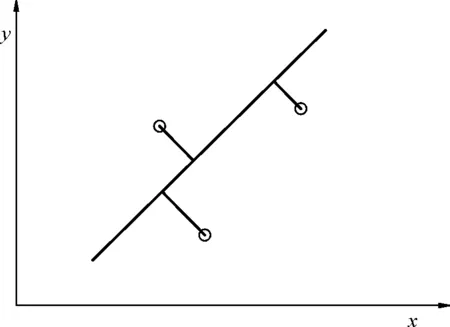
图5　基于距离最短的最小二乘法的偏差

3.2.3引入稳健评估的最小二乘法

在基于距离最短的最小二乘法的基础上，引入稳健评估，即根据偏差的大小，给每个测设点位数据一个新的权重，降低偏差较大的点位对拟合结果的影响。

在基于距离最短的最小二乘法的基础上引入稳健评估，可以减小偏差较大的测设点位数据对拟合结果的影响，效果优于上述两种拟合方法。

结合纵断面线形可能存在一些点位发生了较大偏差的情况，因此，在纵断面线形的拟合中，可以考虑采用引入稳健评估的最小二乘法来分别拟合纵断面线形中的直线和竖圆曲线，得到更加优化的线形拟合参数。

4　纵断面线形的优化

在纵断面线形分段和拟合的基础上，可以得到满足偏差最小的直线和纵断面拟合线形，但是在纵断面中，还包含了纵多的约束条件，比如竖曲线与平面缓和曲线不得重合，竖圆曲线与道岔位置不能重合，纵断面中某些点位的最大高程和最小高程满足要求，拟合结果中的直线坡度不得超过允许的最大坡度等，考虑养护维修时，还应对纵断面的直线坡度大小以及竖圆曲线半径大小的取值精度进行约束，即需要对直线线形与竖圆曲线线形拟合结果进行一定的调整，以满足规范和养护维修的要求。

在满足所有约束条件后，得到的直线和竖圆曲线拟合结果才是满足实际工程需求的最终拟合结果，在此基础上，通过计算各个测设点位的起落道量，并将点位恢复至拟合后的参考线形位置，恢复客运专线在纵断面上的平顺性，实现客运专线纵断面线形的重构。

5　结束语

在分析客运专线平面重构的基础上，展开了针对纵断面重构的探讨，阐述了纵断面线形重构的主要思路及方法，为纵断面重构的相关研究提供一定的参考，为了满足实际工程应用，后续工作中，还应开展约束条件如何影响重构结果的研究。