水轮机特性曲面型值点延拓神经网络仿真研究

谭剑波，马孝义，何自立

(1.杨凌职业技术学院，陕西 杨凌 712100；2.西北农林科技大学水利水电科学研究院，陕西 杨凌 712100)

综合特性曲线是根据模型水轮机试验数据绘制而成，是水轮机选型设计和机组过渡过程调节计算的主要依据[1]。目前，厂家提供的综合特性曲线仅停留在模型试验获得的高效工况区曲线，对于小开度、小流量的水轮机运转特性及水力过渡过程尚无完整数据，也很难用单一精确数学模型进行描述。为指导水电站充分利用水力资源，实现水轮机在大小波动范围内安全稳定、高效合理地调控运行。在现有综合特性曲线数据基础上，通过计算机辅助构建低效工况区网络模型，分析预测小开度、小流量区域的流量和力矩特性数据，实现水轮机综合特性曲线的准确延拓。

由于高效工况区流量和力矩数据呈明显非线性特性，常规BP网络学习训练存在较大不适定性，任意较小误差均可能对求解结果带来较大影响[2]。运用文献[3]中彭利鸿等提出的GA-BP神经网络学习模型，在获得ZD450/D32R轴流定浆式水轮机流量和力矩特性三维函数关系相对值数据组成的空间曲面后，采用比例间隔数值延拓算法，对流量和力矩相对值曲面样条曲线进行型值点寻优和延拓，获得全工况区流量和力矩特性相对值数据，以确保机组过渡过程调节计算具有较高可信性和可实施性。

1 水轮机调节特性神经网络建模

1.1 水轮机运转特性关联性函数

影响水轮机流道内水流运动因素较多，且相互间很难用单一线性关系进行描述。研究轴流定浆式水轮机过渡过程过流运转调节性能，应从稳态和动态过程中的水轮机过机流量Q和主动力矩M的运转特性出发。水轮机主动力矩M与过机流量Q、转速n和效率η间的函数关系为：

(1)

目前，工程中还缺乏与实际相匹配的动态模型对水轮机动态调节特性进行试验分析。因此，建立水轮机过渡调节关联性模型时，仍需以静态模型综合特性曲线为基础，在考虑静态特性水头H因素外，还需考虑与流量和力矩动态特性相关联的导叶开度α和机组转速n间的协联关系[4]，其数学函数表达为：

Q=Q(H,α,n)

M=M(H,α,n)

(2)

从水轮机模型综合特性曲线上获得的过机流量数据Q及经式(1)转换运算获得的力矩数据M，在量纲、数量级等方面存在较大差异。根据BP神经网络模型归一化处理要求，采用水机行业通用单位参数(D1M=1 m和HM=1 m标准情况下的特征参数)，形成单位转速n11、导叶开度α与单位流量相对值q11和单位力矩相对值m11间的三维函数关系[3]，即：

q11=Q11/Q110=fq(α,n11)

m11=M11/M110=fm(α,n11)

(3)

式中：Q11、M11和Q110、M110分别为模型转轮的单位流量和单位力矩及在最优工况条件下的单位流量和单位力矩。

从式(3)可知，对于具有多值性的转轮模型综合调节特性曲线，可以转换为由单位转速和导叶开度两个变量确定的流量和力矩空间特性曲面。采用CAD软件与CATIA二次开发技术，结合从水轮机综合特性曲线上自动提取出流量特征相对值数据矩阵[q11]=[α,n11]及经式(1)转换运算获得的力矩特征相对值数据矩阵[m11]=[α,n11]，形成神经网络模型流量和力矩特性的“学习样本”。

1.2 GA-BP神经网络结构

从式(3)可知，流量特性和力矩特性其函数变量相同，学习训练神经网络模型也采用相同结构。由于常规BP神经网络应用存在局部寻优差、收敛速度慢、预测能力与训练能力不匹配等问题。根据文献[3]研究成果，针对水轮机动态调节复杂的非线性特性，建立基于遗传算法改进的三层反向迭代传播神经网络(GA-BP)结构，如图1所示。

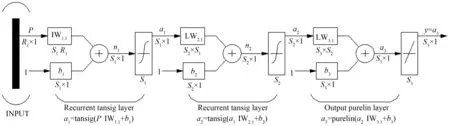
图1 单位流量(力矩)相对值神经网络结构Fig.1 Unit flow (torque) relative value neural network structure

神经网络输入层(Input)输入从水轮机模型综合特性曲线上采集的包含单位转速和导叶开度两个独立变量组成的“学习样本”数据矩阵P[a,n11]。隐含层(Recurrent layer)采用循环交叉牛顿梯度下降迭代运算和双曲正切S型(Tan-Sigmoid)高斯型非线性作用函数，对输入样本进行学习训练。在神经网络结构参数设定中，常规BP神经网络权值与阈值随机自动生成，并进行误差梯度搜索，可能造成结构变动幅度大、迭代计算周期长、全局寻优早熟或滞后、局部寻优极小点死循环等问题。利用遗传算法(GA)群体搜索寻优，经遗传选择、交叉变异及解码赋值等，寻找神经网络结构参数中权值与阈值的最优解，可增强样本学习和数据成果的准确有效性。样本数据经隐含层学习后，经输出层(Output layer)传递函数(Purelin)训练生成力矩和流量关联性数据成果。

2 比例间隔数值延拓算法

GA-BP改进神经网络能够准确处理水轮机综合特性曲线数据，但学习样本数据仅限于厂商提供的模型试验高效工况区。为获得水轮机过渡过程全工况区范围动态调节特性，需将神经网络预测仿真流量和力矩特性曲面，向低效工况区延拓，以真实反映水轮机在各工况条件下的综合调节特性。

2.1 样条曲线型值点与参数约束

曲面延拓根据控制点类型不同，有控制典型数值点(简称：型值点)的曲面延拓和控制网格点的曲面延拓两种方法。流量特性和力矩特性曲面延拓，其主要目的是获得水轮机全局范围准确调节数据，即在现有高效工况区曲面数据基础上，通过合理数值延拓以获得低效工况区数据。如采用控制网格点进行最优曲面延拓，则一些特殊工况点数据将会在数值延拓过程中被计算淹没，导致预测数据不准确。水轮机流量和力矩特性曲面延拓，应采用以典型数值点作为参数控制点的型值点延拓法，形成GA-BP神经网络样本数值延拓的学习训练准则。

空间三维曲面是由若干非线性样条曲线交互组成的网格面耦合形成，对于经式(3)归一化处理后的单位流量和单位力矩曲面，可简化认为由处于0≤x≤1范围内若干样条曲线族A(X)组成。非线性样条曲线A(x)上提取一系列力矩和流量调节特性的工况点数据组成型值点矩阵，即：K[k0,k1,…,kn]，[kn=A(xn)，0≤x≤1]，相应在定义域范围内的x[x0,x1,…,xn]即为样条曲线型值点参数约束点矩阵。样条曲线型值点与对应参数约束点间的相互关系，如图2(a)所示。

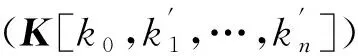
图2 样条曲线型值点优选Fig.2 Optimal choice of spline curve characteristic-points

从图2(b)可知，型值点与参数约束点间是一一对应，在0≤x≤1定义范围内参数约束点密度与型值点密度呈正比例线性关系，且两者数量相等，则可将样条曲线型值点组合寻优转变为求控制多边形的顶点组合寻优[5]。

2.2 比例间隔型值点延拓

样条曲线A(x)采用“先离后合”的思想，按比例间隔分布采用控制多边形顶点在0≤x≤1定义区间范围内的分布密度，来确定最优型值点矩阵序列[6]，其函数表达为：

(4)

为简化计算，式(4)先作以下规定，即：x0=k0=p0=0；xn=kn=pn=1；ki=A(xi)。曲线型值点的参数约束点xi由标准值xie和误差修正值ε两部分构成，则式(4)可转换为：

xi=xie+εi=1,2,…,n-1

(5)

曲线型值点参数约束点xi的标准值为：

(6)

在0≤x≤1范围内，如型值点个数越多则其密度值越高，相应通过型值点插值逆演运算获得的样条曲线与原曲线越匹配[6]。为使型值点组合真实全面反映样条曲线特征，需引入误差修正附加分量进行约束，即：

(7)

BP神经网络进行型值点容差分析时，对不满足容差条件的参数约束点采取比差修正，直到满足容差范围获得新延拓型值点为止。比差修正表达式为：

(8)

将待延拓曲面上样条曲线族A(X)，经比例间隔运算获得的曲面所有特征型值点组成一个线性矩阵[M]：

(9)

以GA-BP神经网络经学习训练获得的高效工况区单位流量和单位力矩相对值样条曲线的型值点集矩阵[M]，按切向延伸法即可实现向低效工况区延伸，获得小开度、小流量等工况区单位流量和单位力矩调节特性数据。

3 GA-BP神经网络仿真实验

3.1 原始数据处理

从ZD450/D32R综合特性曲线(桨叶角度φ=+15°)，提取转轮高效工况区的单位流量相对值数据，并经式(1)转换获得单位力矩相对值数据，作为学习样本Pq(a,n11)和Pm(a,n11)。利用Matlab7.0中的Simulink模块，根据图1编写神经网络仿真模型，并按GA群体寻优及比例间隔型值点延拓算法，编写trianlm()函数对网络模型进行连接通道权值和阈值的自动学习训练及型值点延拓。

3.2 网络模型参数设置

从式(3)可知，定浆式水轮机转轮力矩和流量特性包含导叶开度和单位转速两个自变量，相应神经网络Input输入层设置2个神经元。Recurrent隐含层采用Tan-Sigmoid高斯型非线性作用函数，其神经元个数与运算精度密切相关，过多会引起计算量增大而增长运算周期，过少会降低运算结果精确度[7]。经模型多次试算及类似优秀网络模型参数，设置10个神经元，即隐含层一层(S1)和隐含层二层(S2)均为10个神经元。网络模型输出为单位力矩或单位流量，则Output输出层采用1个Purelin纯线性函数神经元。神经网络模型训练参数为：显示间隔.trainParam.show=50；最大训练步数.trainParam.epochs=300；训练误差.trainParam.goal=0.01；学习速率.trainParam.lr=0.05。

3.3 仿真图形

GA-BP神经网络学习训练结束后，对任意样本数据Pq(a,n11)或Pm(a,n11)利用仿真函数newff()可获得对应仿真结果[8]。ZD450/D32R轴流定浆式水轮机(桨叶角度φ=+15°)的单位流量和单位力矩相对值曲面仿真，可由如下运算函数实现：

m11=newff([2,10,1],{Pm,W1,b1,'tansig',W2,b2,'tansig',W3,b3,'Purelin'},'traingdx', 'learngdm')

q11=newff([2,10,1],{Pq,W1,b1,'tansig',W2,b2,'tansig',W3,b3, 'Purelin'}, 'traingdx', 'learngdm')

经GA-BP神经网络学习训练，得到模型转轮高效工况区的单位流量和单位力矩相对值仿真曲面，如图3和图4所示。

图3 高效工况区单位流量相对值曲面Fig.3 Unit flow relative value surface in efficient area

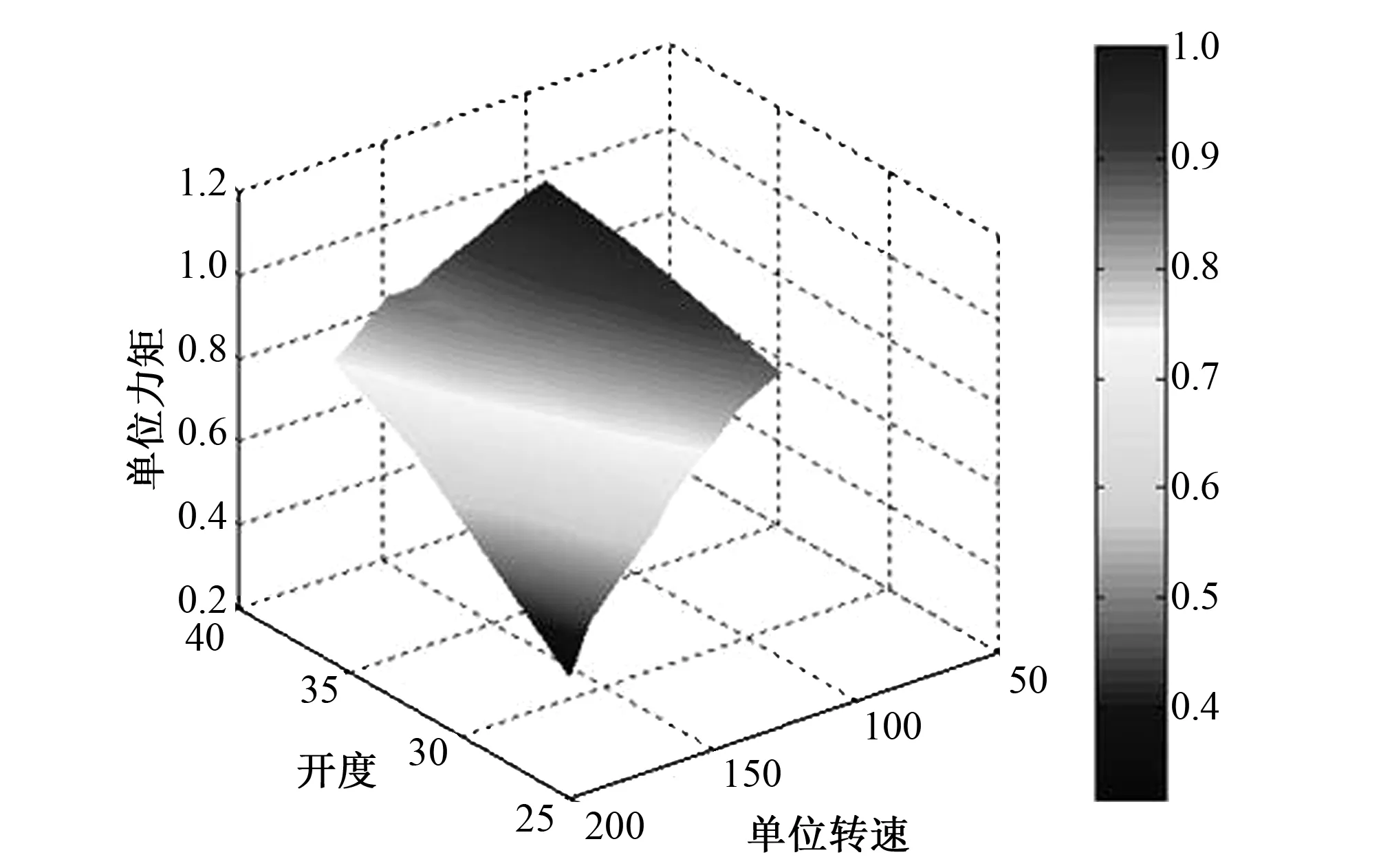
图4 高效工况区单位力矩相对值曲面Fig.4 Unit torque relative value surface in efficient area

GA-BP神经网络模型对流量和力矩样本进行学习训练后，经比例间隔型值点延拓算法，即可获得水轮机包含小流量、小开度等特殊工况点的全工况区调节特性，其延拓曲面如图5和图6所示。

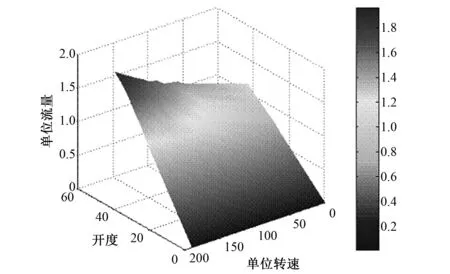
图5 全工况区单位流量相对值延拓曲面Fig.5 Unit flow relative value surface in all area

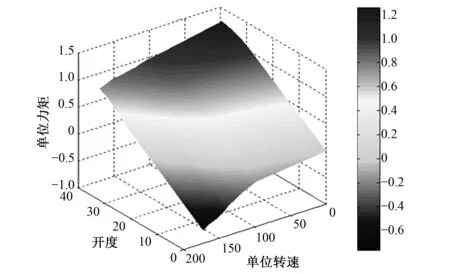
图6 全工况区单位力矩相对值延拓曲面Fig.6 Unit torque relative value surface in all area

3.4 仿真结果分析

从高效工况区单位流量、单位力矩相对值和全工况区单位流量、单位力矩相对值延拓仿真曲面，可以看出基于GA遗传算法和比例间隔型值点延拓算法的神经网络模型，对模型转轮调节的流量和力矩曲线型值点提取、型值点延拓及仿真曲面拟合的效果很好，能够真实反映水轮机在全工况区范围内的综合调节特性。

由于单位流量和单位力矩相对值仿真模型结构和参数设置均相同，网络模型误差特性相近，选择单位力矩相对值进行分析。从图6提取两组数据与模型转轮试验值进行误差分析，如表1所示。

表1 单位力矩相对值神经网络输出与试验数据对比Tab.1 Unit torque relative value compare between neural network output and model test

GA-BP神经网络通过模拟自然进化过程群体寻优，不断调整和修正神经元间的连接权值和阈值，使模型预测值与水轮机实际调节特性更加匹配。由图6及表1可知，经比例间隔型值点延拓和神经网络曲面拟合训练后，误差均控制在±0.007范围内，说明网络模型结构及参数设置合理、建模精度高。全工况区范围内的流量和力矩相对值延拓曲面光滑度好、非线性拟合效果好，能真实反映水轮机在不同工况条件下的调节特性。

4 结 语

水轮机模型转轮综合特性曲线上获得的流量数据及经转换运算获得的力矩数据，仅能体现高效工况区水轮机调节特性，不能真实反映水轮机在小流量、小开度等

特殊工况点的调节特性。引入神经网络非线性无限逼近功能，建立了一个基于高效工况区流量和力矩相对值数据样本的水轮机调节GA-BP神经网络非线性拟合模型，并采用比例间隔型值点延拓算法对流量和力矩相对值曲面进行延拓。可得如下结论。

(1)采用单位参数按归一化处理要求，建立以水轮机单位转速和导叶开度为变量的单位流量和单位力矩相对值三维函数关系，将具有多值性的水轮机转轮模型综合调节特性曲线，转化为由两个独立变量确定的空间特性曲面。

(2)运用改进遗传算法优化BP神经网络，通过流量和力矩相对值样本数据自动学习训练，生成高效工况区调节特性的流量和力矩相对值曲面，实现水轮机综合特性曲线的数值化处理和智能预测分析。

(3)基于比例间隔型值点延拓算法的神经元自动运算，生成可以直观反映全工况区水轮机动态调节运行特性的流量和力矩相对值延拓曲面。这为探究水轮机全工况区调节特性提供了一种新方法，并为机组大小波动过渡过程调节保证计算和电站安全、稳定运行提供了准确的数据支撑。

□

参考文献：

[1] 张蓉生,刘 泽,王立闯,等.基于Delaunay三角网剖分的水轮机综合特性曲线数据插值[J].水力发电学报,2011,30(4):198-201.

[2] 谢 进,陈启卷,李俊益.基于BP神经网络的水轮机调节系统建模与仿真[J].水利水电技术,2015,46(3):119-122.

[3] 彭利鸿,宋 媛,刘 冬,等.基于GA-BP神经网络的水轮机非线性建模方法研究[J].中国农村水利水电,2017,(4):184-188.

[4] 陈飞勇.混流式水轮机综合特性曲线的数值化探讨[J].水动力学研究与进展,1993,8(1):66-72.

[5] 李 青,张文杰,陈 菁.指纹曲线数值拟合方法的对比和优选[J].现代电子技术,2015,38(24):27-30,35.

[6] 陈素根,赵正俊.拟三次三角B样条曲线曲面构造及其应用[J].小型微型计算机系统,2015,(6):1 331-1 335.

[7] 黄文涛,常 黎,黄正军.基于BP网络的水泵水轮机全特性空间曲面描述[J].水电能源科学,2014,31(12): 205-209.

[8] 张 培,陈光大,张 旭.BP和RBF神经网络在水轮机非线性特性拟合中的应用比较[J].中国农村水利水电,2011,(11):125-128,131.