高温高压气体在低含水率介质中迁移的数值模拟
, ,
(西北核技术研究所,西安 710024)
1 引 言
探索高温高压气体在多孔介质中的运动规律具有广泛的应用背景,可用于地下爆炸实验中的气体输运[1]和温室气体减排中的二氧化碳地质封存[2]。实际的地介质中可能含有地下水,因此气体在地介质中的运动本质上是一个气液两相渗流过程,属于渗流力学的研究前沿问题。
Nitao[3]开发的NUFT程序可用来模拟污染物在地介质中的运移,如Carrigan等[4]利用USNT模块对地下核爆炸后氙的放射性同位素的迁移行为进行了模拟;Pruess等[5]开发的TOUGH2系列程序是目前研究多相多组分非等温渗流的主流软件之一,文献[6]利用该程序对内华达试验场的尤卡山进行了试验场尺度的研究;Flemisch等[7]开发的DuMux是一个模拟多孔介质内流体运移过程的开源软件,涵盖众多模型,如三相三组分非等温渗流模型[8]等。
姜广辉[9]对裂隙岩体中气液两相的渗流特性进行了实验测量和理论分析,研究了裂隙中气液两相的渗流机制;蒋兰兰[2]设计并搭建了核磁共振成像和X射线CT成像实验平台,进行了CO2排泄和吸吮的初步实验;鞠斌山等[10]建立了多组分非等温CO2混相驱动模型,考虑了对流、弥散、吸附以及储层破坏现象;何增等[11]建立了气液两相多组分非等温渗流的数学模型,并与气体渗流模型进行了比较。
对比可以看出,国外在该领域已形成众多成熟的软件和模拟器,而国内在数学模型和数值模拟方面的进展尚不充分。本文将针对文献[11]的数学模型发展适宜的数值离散方法,并对高温高压气体在低含水率地介质中的输运过程进行数值模拟,主要研究多孔介质的孔隙度和渗透率对气体迁移的影响。
2 数学模型
气液两相多组分非等温渗流的数学模型,参考文献[11]。两相为液相(l)和气相(g),用下标α表示;组分为水(w)、空气(a)和示踪物(t),用上标κ表示。考虑的物理机制有对流、弥散、热传导、热辐射、气体压缩性以及水在气液两相间的平衡。
2.1.1 连续性方程
以组分为研究对象建立连续性方程。水的连续性方程为

(1)
空气和示踪物的连续性方程为

(κ=a,t) (2)
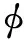
2.1.2 运动方程
多孔介质中流体的运动方程为达西定律[12],即

(3)

2.1.3 能量守恒方程
考虑对流传热、弥散传热以及热传导,建立能量守恒方程为

(4)
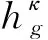
2.2.1 气体的状态方程
对气体采用理想气体状态方程。气体的总压等于各组分气体的分压之和,即
(5)

(6)
本文使用国际水及水蒸气性质协会推荐的水的饱和蒸汽压公式[16]。该公式的误差小于0.1%,但形式较为复杂,指数项包含6项,其中3项为整数次幂,3项为半整数次幂。
2.2.2 相对渗透率
相对渗透率kr α一般简化为有效饱和度Se的函数,如常用的相对渗透率表达式[13,17]为
kr l=Sne,kr g=(1-Se)n
(7)
式中n=3可用于模拟考虑毛细压力的情形[17]。有效饱和度Se的定义为
(8)
式中Sα r为α相的残余饱和度。
2.2.3 毛细压强
多孔介质中气液两相的压强在分界面处并不连续,其差值称为毛细压强pc,即
pc=pg-pl
(9)
毛细压强一般也简化为有效饱和度的函数,本文使用Leverett[18]给出的关系式
2.120(1-Se)2+1.263(1-Se)3]
(10)
式中σ为气液两相间的表面张力系数。
3 数值方法
气液两相非等温渗流的数学模型呈现出高度非线性的特征,主要表现在非达西流动、水蒸气和液态水的平衡以及复杂的本构关系(如水的饱和蒸汽压公式)等方面,因此合理的离散方案对数值求解至关重要。
在多相非等温渗流中,可能会发生相的出现与消失。处于不同的相时,完整描述该系统所需要的独立变量也不同,这组变量称作首要变量,其他量称作次要变量。根据吉布斯相率,一个多相多组分系统的自由度数F为[8]
F=C-P+2+(P-1)=C+1
(11)

表1总结了三种相态的首要变量和相出现的条件,图1给出了完整的相态转变准则。可以看出,PS1和PS2、PS1和PS3之间可直接转变,而PS2和PS3的转变则需要经历PS1的中间相态,表现为需要更多的迭代求解。此外,水的连续性方程在PS3时为椭圆型方程,而在其他相态时为抛物型方程,为设计统一的算法带来额外的复杂性。本文采取最低饱和度法简化问题[19],即假设气相总是存在,并设定最低饱和度(如Smin=10-6)避免气液共存时相的消失。也就是说,利用相态PS1在Sg=Smin的极限情形来近似PS3,从而减少相态转变的判断。此外,通过分析可知,无论处于相态PS1还是PS2,未知数个数与方程数目都相等,即该问题是封闭的。
空间离散主要解决通量的计算问题。观察控制方程可以发现,运动方程与时间无关,使用中心差分离散;连续性方程和能量方程均具有守恒方程的形式,使用有限体积法离散,其中,对对流项采用迎风格式,对扩散项采用中心差分格式。计算通量还需要处理参数在界面的等效值[6,11]。
设Δtn=tn +1-tn,并利用fn+1,m表示物理量f在时间步长Δtn后的第m步迭代值,迭代初值
表1 相态类型、首要变量以及相出现的条件
Tab.1 Phase states,corresponding primaryvariables and conditions for phase appearance

PhasestatePresentphasesPrimary variablesAppearance of phaseLiquidGasPS1l,gSl,Xwg,pg,T——PS2gXwg,Xag,pg,TT
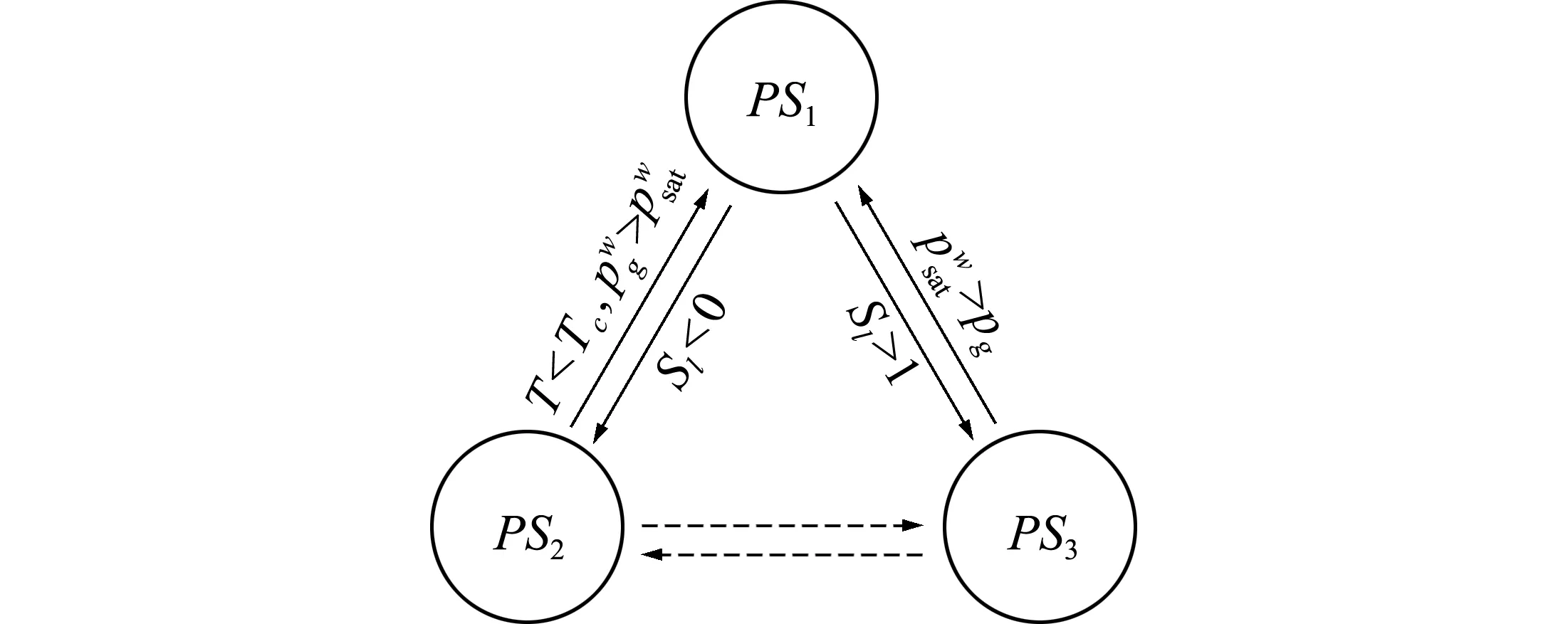
图1 相态转变准则
Fig.1 Criteria of phase transition
fn +1,0=fn。记控制方程的通量为Fnβ,下标β可取w,a,t和e,分别表示水、空气以及示踪气体的连续性方程和能量守恒方程。计算步骤如下。
(1)m=0。

(4) 求解水的连续性方程
(12)

(5) 将Sn+1,m+1g代入空气和示踪气体的连续性方程,
(κ=a,t)(13)
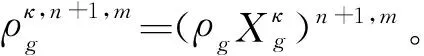
(6) 更新气相状态
(14)
(κ=a,t) (15)
(7) 将饱和度和气相状态代入能量守恒方程
(16)
求解得到Tn +1,m +1,其中Et为单元的总能量,在已知密度和饱和度时仅依赖于温度,如在比热容为常数时,Et与温度呈线性关系。
(8) 将温度Tn +1,m +1代入水蒸气分压方程式(6),更新水蒸气密度为
(17)
(9) 修正气相状态

(18)

(κ=w,a,t)(19)
(10) 计算流体压强
(20)
(21)
(11)m=m+1,重复步骤(4~10),直至达到收敛标准,最后将收敛的数值解更新为tn +1时刻的数值, 即fn+1=fn+1,m+1。

4 计算结果与讨论
采用第3节的模型和算法,编制了二维柱对称坐标系下求解气液两相非等温渗流的计算程序。文献[11]对数学模型的有效性进行了检验。本节研究高温高压气体在低含水率地介质中的输运问题。
求解问题如下,研究域是半径为50 m的球体,中心处是半径为5 m的高温高压气体区,称作空腔。在初始时刻,空腔内充满了水蒸气、空气和一氧化碳,质量分别为802 kg,1356 kg和1727 kg,温度为2000 K,压强为4.86 MPa;研究域的其余位置与外界环境达到平衡,外界环境不含一氧化碳,气体压强为1 atm,温度为20 ℃。主要计算参数列入表2。

图2 Picard迭代法在一个循环内部的完整流程
Fig.2 Complete flow chart of the Picard iteration method
表2 主要计算参数
Tab.2 Main parameters used in the calculation

K10-13 m2μl1.00×10-3 Pa·sSgr0ϕ0.01μκg1.80×10-5 Pa·sε0.9ρl998.2 kg/m3Slr0.1

(22)

结果表明,气体在低含水率介质和等效孔隙度的干燥介质内的迁移行为基本一致。
图4展示了孔隙度为0.010且渗透率为10-13m2条件下,空腔内温度和液态水质量的时间历程。由于空腔内的初始温度高于水的临界温度647.1 K,因此水只能以水蒸气的形式存在。随着空腔内的温度和压强降低,在842 s时,空腔温度下降到115.3 ℃,水蒸气分压为1.713×105Pa,等于该温度下的饱和蒸汽压,液态水开始出现。需要注意的是,该算例中水的相态转变温度大于100.0 ℃,这是由于水蒸气的分压大于一个标准大气压。在842 s时刻,空腔温度下降的趋势减缓,这是因为水蒸气液化会释放大量的潜热。随着温度降低,液态水逐渐增多,但同时也在压差作用下向周围多孔介质中渗透。在约104s后,空腔温度基本保持不变,液态水的质量由于向外渗出而逐渐减少。

图3t=3600 s时刻示踪气体质量分数的分布(不同含水率)
Fig.3 Distribution of mass fractions of gas tracer att=3600 s,with different water contents
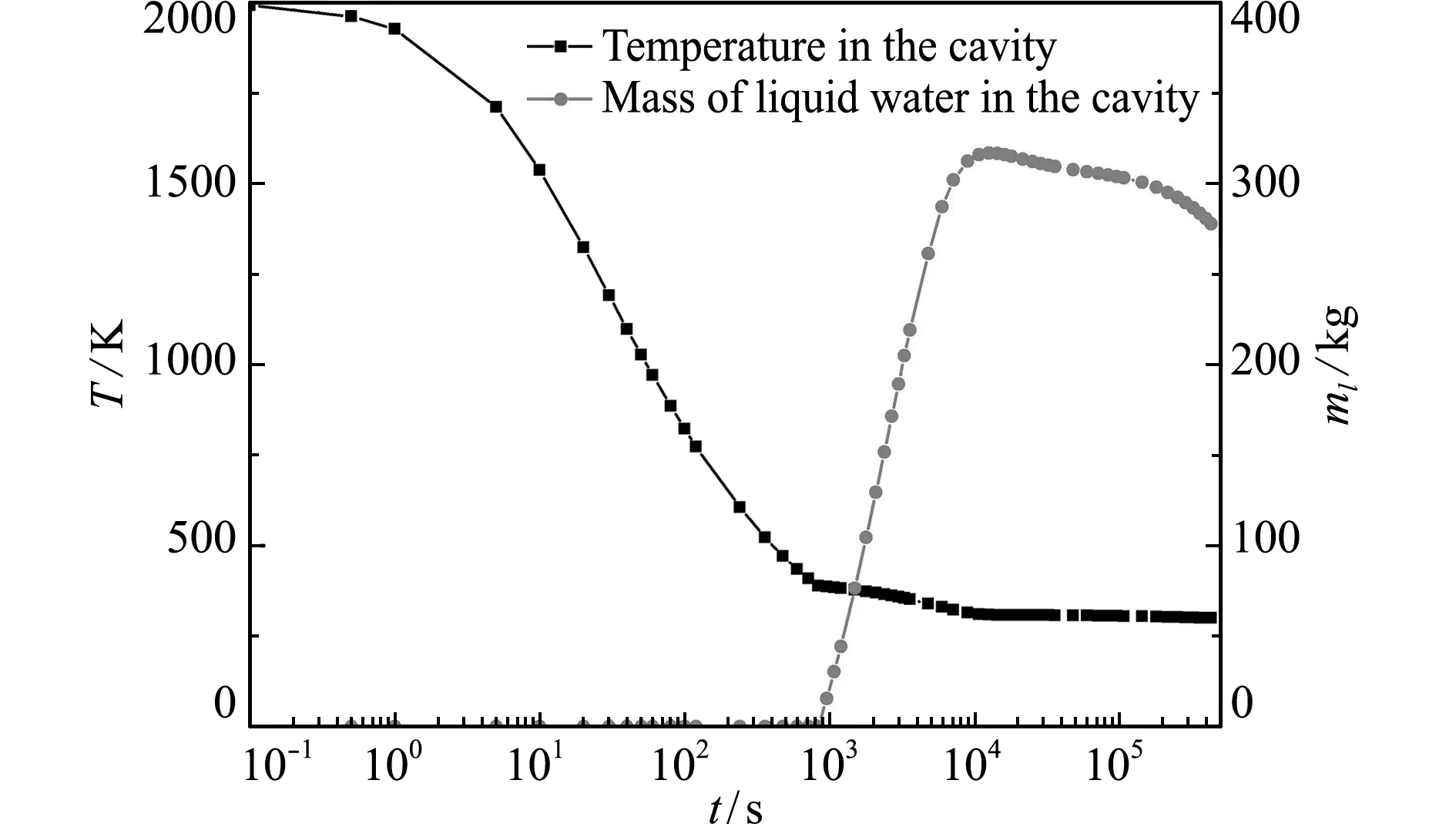
图4 空腔内温度和液态水质量的时间历程
Fig.4 Time history of temperature and mass of liquid water in the cavity
4.3.1 孔隙度
图5展示了不同孔隙度下气相压强和示踪气体份额在600 s时刻的分布,渗透率固定为10-13m2。可以看出,孔隙度越小,渗流发展得越快。这是因为孔隙度越小的介质内气压越大,向外推进的速度也越大,最终造成上述现象。也可以理解为孔隙度对空腔内气体演化的影响很小,如图6所示,为了容纳大致等量的气体,孔隙度小的介质所需的体积更多,即气体运动的距离越远。

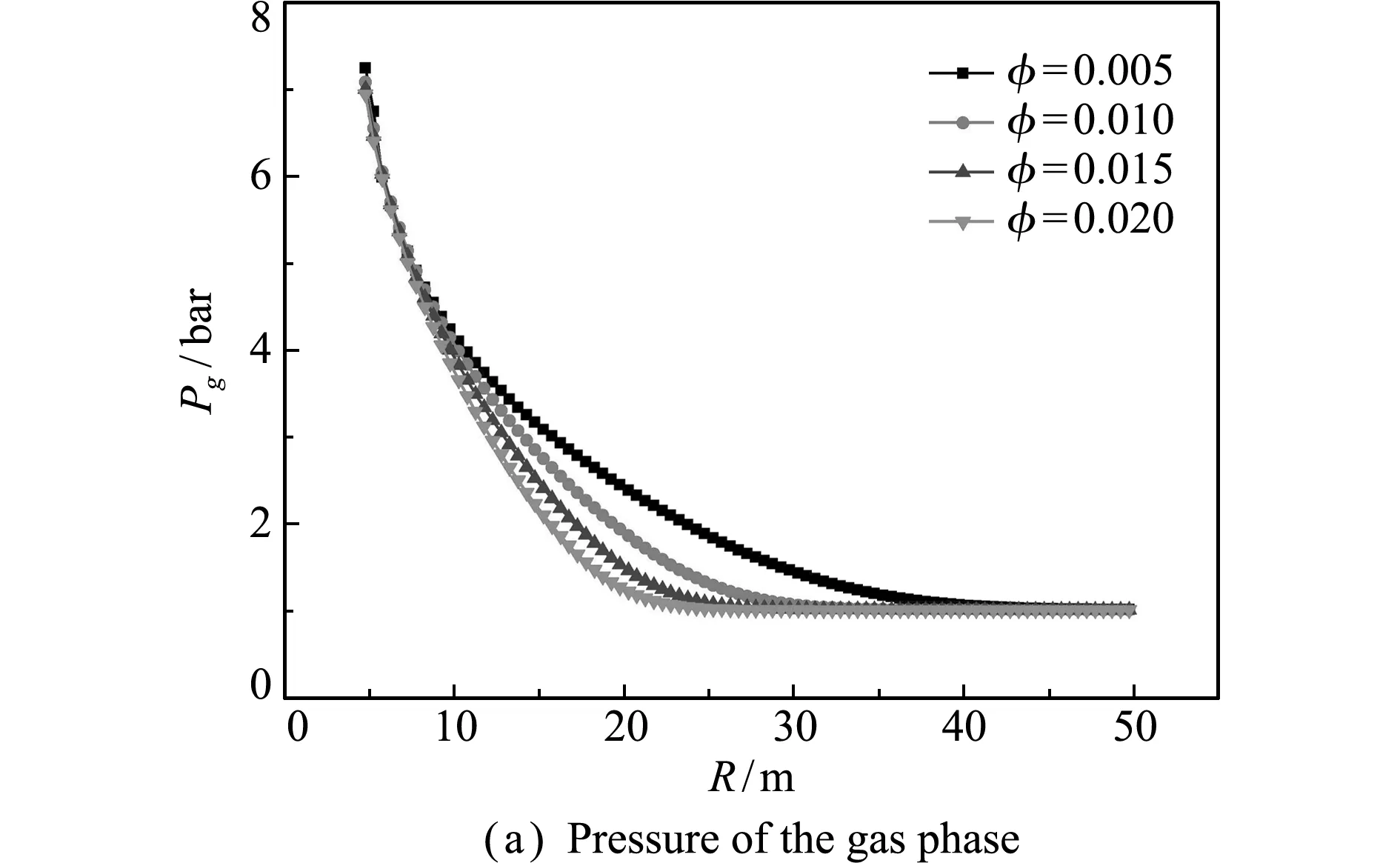

图5t=600 s时刻气相压强和示踪气体份额的空间分布(不同孔隙度)
Fig.5 Distribution of gas pressure and mass fraction of gas tracer att=600 s,with different porosities
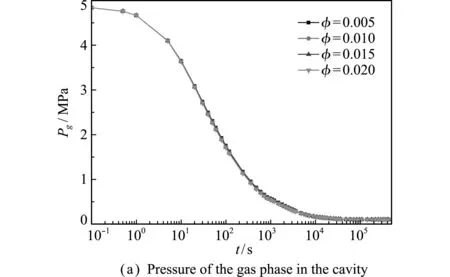



图6 气相压强和示踪气体份额的时间历程(不同孔隙度)
Fig.6 Time history of gas pressure and mass fraction of gas tracer,with different porosities
(23)
表3t=600 s时刻示踪气体迁移距离的模拟值与估算值的比较(不同孔隙度)
Tab.3 Comparisons between the simulated and evaluated values of the transport distance of gas tracer att=600 s,with different porosities

ϕ0.0050.0100.0150.020Rc/m29.84(29.72)23.6320.63(20.68)18.70(18.81)
图6展示了空腔内和R=5.25 m处气相压强和示踪气体份额的时间历程。孔隙度对空腔内气体演化的影响很小,但在空腔外则不同。由于孔隙度小的介质容纳气体的空间小,因此气相压强更大。来自空腔的气体将与孔隙内的气体混合,对于孔隙度小的介质,混合过程将更为迅速,即示踪气体份额上升更快。
4.3.2 渗透率
图7展示了不同渗透率下,气相压强和示踪气体份额在600 s时刻的分布,孔隙度固定为0.010。根据达西定律,渗透率越高,气体速度越快,流动影响的范围也越大,如K=10-12m2对应的气相压强已接近平衡。


图7t=600 s时刻气相压强和示踪气体份额的空间分布(不同渗透率)
Fig.7 Distribution of gas pressure and mass fraction of gas tracer att=600 s,with different permeabilities

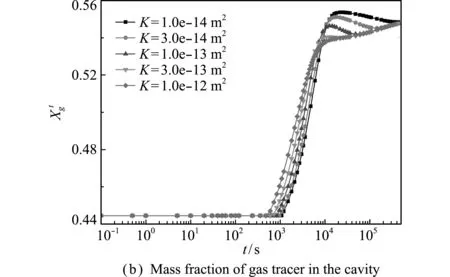
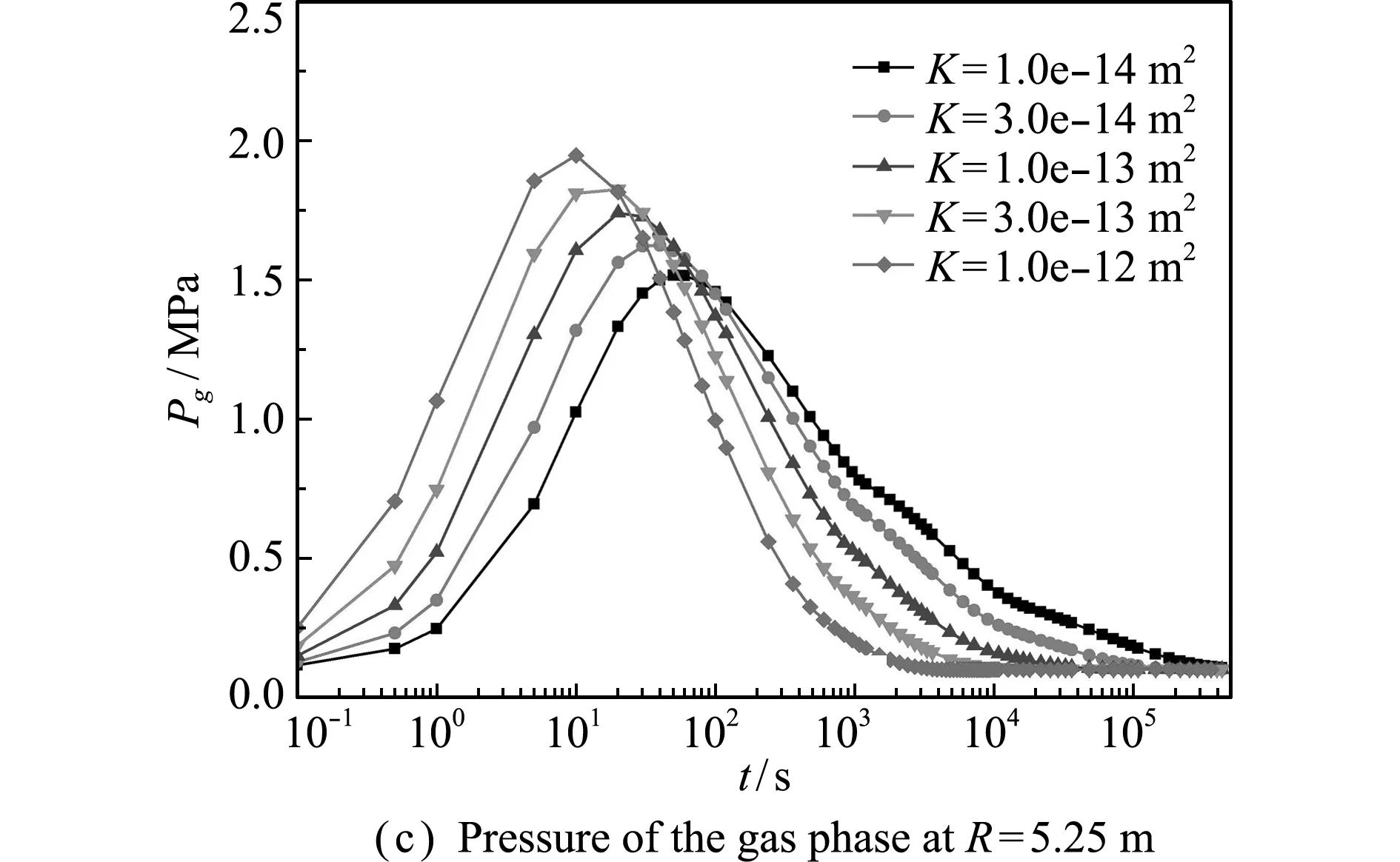
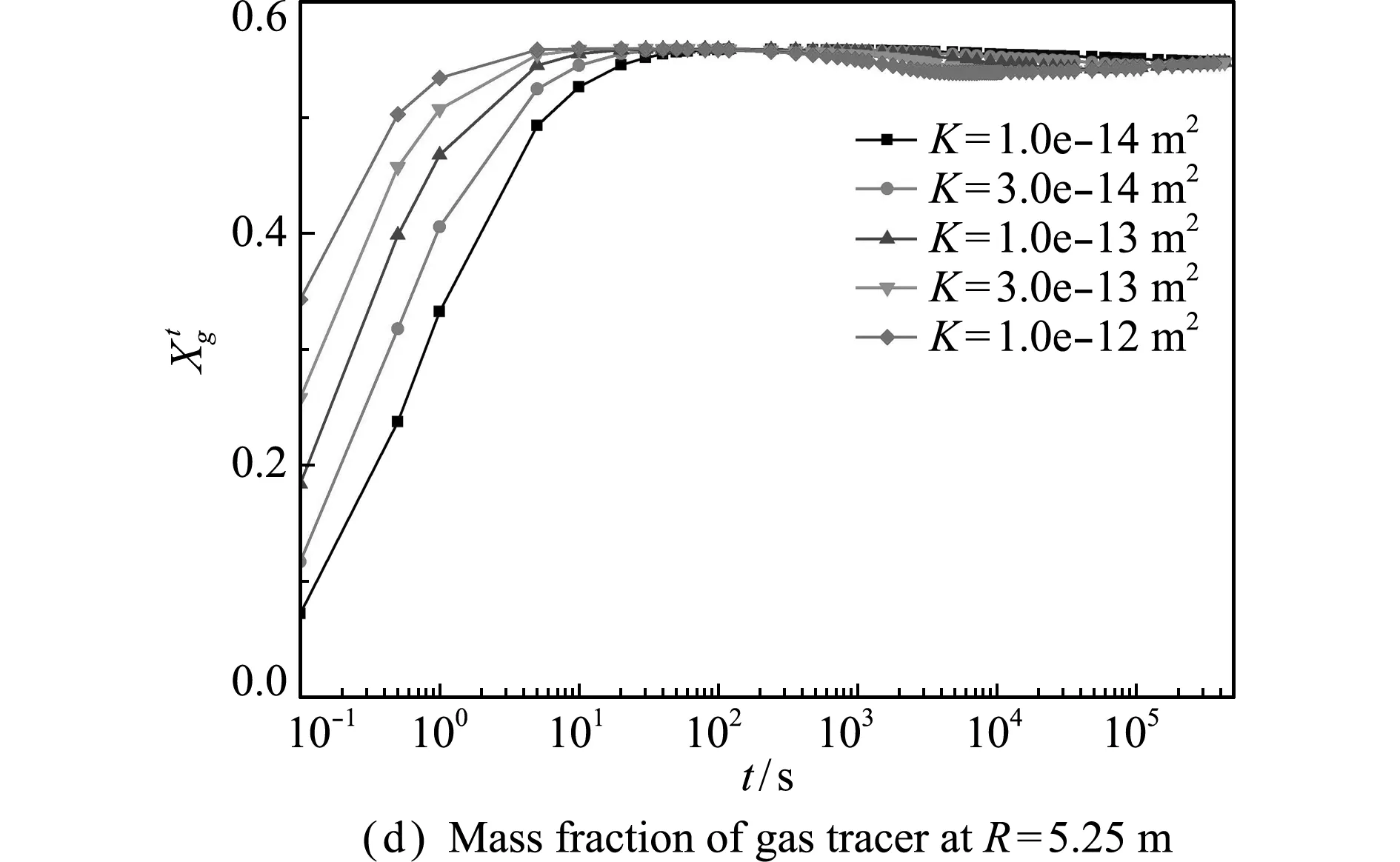
图8 气相压强和示踪气体份额的时间历程(不同渗透率)
Fig.8 Time history of gas pressure and mass fraction of gas tracer,with different permeabilities
表4列出了示踪气体在两个时刻的迁移距离。通过分析数据,发现渗透率K与迁移距离Rc的5次方近似成正比,即
(24)
表4括号内给出了由式(24)估算的Rc,以K=10-13m2的数据为基准。除了在边界处差异较大外,估算值与计算值均吻合较好,误差在4%以内。
图8展示了空腔内和R=5.25 m处气相压强和示踪气体份额的时间历程。与孔隙度不同,渗透率对空腔和介质中的物理量均有明显的影响。渗透率越高,空腔内气相压强下降越快,示踪气体份额上升越快,介质中的气相压强和示踪气体份额上升越快,这显然是由渗流速度更快引起的。
表4 不同时刻示踪气体迁移距离的模拟值与估算值的比较(不同渗透率)
Tab.4 Comparisons between the simulated and evaluated values of the transport distance of gas tracer at different times,with different porosities

K/m21.0×10-143.0×10-141.0×10-13t=600 s14.42(14.91)18.23(18.57)23.63t=3600 s21.39(21.84)27.41(27.20)34.61K/m23.0×10-131.0×10-12t=600 s29.54(29.44)36.67(37.45)t=3600 s41.58(43.11)45.04(54.85)
5 结 论
本文简单介绍了两相多组分非等温渗流的数学模型,并建立了适宜的离散方法对其进行数值求解。通过分析控制方程性质和相态转换准则,采用最低饱和度法降低算法的复杂性。使用有限体积格式进行空间离散,并针对控制方程组高度非线性的特点,设计了一套专门的Picard迭代法进行时间离散,解决了气液两相渗流的强耦合问题。
利用该算法对高温高压气体在低含水率介质中的迁移行为进行了模拟。证明了利用等效孔隙度的干燥介质近似低含水率介质的有效性,并分析了空腔内的气液相变转换过程。在此基础上,初步得到了孔隙度和渗透率对气体输运的影响规律,着重研究了示踪气体迁移距离。计算结果表明,在相同的渗透率下,迁移距离随孔隙度减小而增加;在相同的孔隙度下,迁移距离随渗透率增加而增加。本文的模型和方法也可用于高含水率介质中气体迁移行为的研究。
:
[1] 乔登江.地下核爆炸现象学概论[M].北京:国防工业出版社,2002.(QIAO Deng-jiang.IntroductiontoUndergroundNuclearExplosionPhenomenology[M].Beijing:National Defense Industry Press,2002.(in Chinese))
[2] 蒋兰兰.CO2地质封存多孔介质内气液两相渗流特性研究 [D].大连理工大学,2014.(JIANG Lan-lan.Study on Gas/Liquid Flow Characteristic in Porous Media During CO2Geological Storage [D].Dalian University of Technology,2014.(in Chinese))
[3] Nitao J J.Reference Manual for the NUFT Flow and Transport Code,Version 3.0 [R].Report UCRL-MA-130651-REV-1,Lawrence Livermore National Laboratory,Livenmore,CA,2000.
[4] Carrigan C R,Sun Y W,Hunter S L,et al.Delayed signatures of underground nuclear explosions [J].ScientificReports,2016,6:23032.
[5] Pruess K,Oldenburg C M,Moridis G J.TOUGH2 User’s Guide,Version 2 [R].Report LBNL-43134,Lawrence Berkeley National Laboratory,Berkeley,CA,1999.
[6] Wu Y S,Pruess K.Numerical simulation of non-isothermal multiphase tracer transport in heterogeneous fractured porous media [J].AdvancesinWaterResources,2000,23(7):699-723.
[7] Flemisch B,Darcis M,Erbertseder K,et al.DuMux:DUNE for multi-{phase,component,scale,phy-sics,...} flow and transport in porous media [J].AdvancesinWaterResources,2011,34(9):1102-1112.
[8] Class H,Helmig R,Bastian P.Numerical simulation of non-isothermal multiphase multicomponent processes in porous media.:1.An efficient solution technique [J].AdvancesinWaterResources,2002,25(5):533-550.
[9] 姜广辉.裂隙气液两相渗流特性试验研究 [D].中国矿业大学,2014.(JIANG Guang-hui.Experimental Research on Gas-Water Two Phase Flow Characteristics in Rock Fractures[D].China University of Mining and Technology,2014.(in Chinese))
[10] Ju B S,Wu Y S,Qin J S,et al.Modeling CO2miscible flooding for enhanced oil recovery [J].PetroleumScience,2012,9(2):192-198.
[11] 何 增,田 宙,王铁良.气液两相多组分非等温渗流的数学模型 [J].现代应用物理,2016,7(2):021001.(HE Zeng,TIAN Zhou,WANG Tie -liang.Mathematical model for non-isothermal liquid-gas two -phase multi-component seepage flow in porous media [J].ModernAppliedPhysics,2016,7(2):021001.(in Chinese))
[12] 孔祥言.高等渗流力学(第二版)[M].合肥:中国科学技术大学出版社,2010.(KONG Xiang-yan.AdvancedMechanicsofFluidsinPorousMedia(SecondEdition)[M].Hefei:University of Science and Tech-nology Press,2010.(in Chinese))
[13] Jambhekar V A.Forchheimer Porous-Media Flow Models:Numerical Investigation and Comparison with Experimental Data [D].Universität Stuttgart,2011.
[14] 王铁良,曹 渊,张建鑫.地下爆炸空腔压力和温度历程数值模拟 [J].计算物理,2011,28(5):713-718.(WANG Tie -liang,CAO Yuan,ZHANG Jian-xin.Numerical simulation of cavity pressure and temperature in underground detonation [J].ChineseJournalofComputationalPhysics,2011,28(5):713-718.(in Chinese))
[15] 杨世铭,陶文铨.传热学(第三版)[M].北京:高等教育出版社,1998.(YANG Shi-ming,TAO Wen-quan.HeatTransfer(ThirdEdition)[M].Beijing:Higher Education Press,1998.(in Chinese))
[16] Wagner W,Pruв A.The IAPWS formulation 1995 for the thermodynamic properties of ordinary water substance for general and scientific use [J].JournalofPhysicalandChemicalReferenceData,2002,31(2):387-535.
[17] Chueh C C,Bangerth W,Djilali N.Integrated adaptive numerical methods for transient two-phase flow in heterogeneous porous media [A].Seventh International Conference on Computational Fluid Dynamics[C].Hawaii,2012.
[18] Leverett M C.Capillary behavior in porous solids [J].TransactionsoftheAIME,1941,142(1):152-169.
[19] Abriola L M,Pinder G F.A multiphase approach to the modeling of porous media contamination by organic compounds:2.Numerical simulation [J].WaterResourcesResearch,1985,21(1):19-26.

