薄膜断裂和穿透的向量式有限元分析及应用
, ,
1 引 言
薄膜结构的断裂和穿透破坏过程是一类重要且同时存在几何、材料及接触非线性的复杂不连续行为[1]。具体实例主要有强台风或雨雪作用下的膜材撕裂、物体撞击作用下的穿透过程以及充气气球的充气破裂等。
目前,主要通过理论、试验及统计等方法分析膜材的撕裂强度。吴明儿等[2]针对梯形形状的薄膜试件进行了拉伸破坏试验,研究各向异性膜材在经纬向撕裂时的破坏强度。陈国华[3]基于薄膜材料的拉伸束链模型,模拟并预估了其断裂破坏过程及相应的断裂破坏强度。Aldrich-Smith等[4]对拉伸应力作用下脆性膜/基材料的预先开裂这一典型失效破坏进行了研究。杨班权等[5]研究了残余应力作用对脆性薄膜材料撕裂行为的影响,并推导了该膜材裂纹密度随残余应力变化情况的理论关系式。至于暴雨、冰雹及物体等撞击作用下膜材的穿透破坏,目前主要考虑撞击后的膜材弹性动力响应和变形。宋维举[6]利用 LS -DYNA 对刚性小球撞击薄膜的动力过程进行研究,模拟了其在冲击作用下的大挠度振动响应。膜材的断裂和穿透过程具有复杂不连续性,已有文献尚未有通过有限单元法对其破坏全过程进行的数值研究,本文研究方法将为该类型问题的模拟计算提供一种新的解决方案。
向量式有限元VFIFE(Vector Form Intrinsic Finite Element)[7-9]通过点值描述和向量力学分析来获得结构体系的行为。各质点运动方程在每个循环子步中解耦并独立逐步求解,解耦后的显式差分方程不存在集成的大规模刚度矩阵,也无需进行迭代计算,在结构大变形大转动、断裂及穿透等复杂不连续行为分析中具有较好的应用。对于结构断裂和穿透问题,在统一的主分析程序中,前者引入断裂失效准则和质点分裂实现模块,后者同时引入碰撞和断裂机制模块;在不增加计算难度和大量计算工作的基础上,通过结构构形的步步更新可有效跟踪获得其变形、断裂及穿透破坏全过程。
本文基于向量式有限元薄膜单元理论,研究了薄膜结构的断裂失效和穿透破坏行为。前者采用失效应力判断准则,提出了向量式有限元质点分裂的断裂实现方式,后者则同时结合碰撞和断裂实现机制,有效模拟了薄膜结构的变形、断裂及穿透破坏全过程。编制了薄膜结构的断裂和穿透求解程序,并通过算例分析验证了理论和程序的可靠性和有效性。
2 向量式膜单元理论
向量式有限元法通过质点系的运动过程来模拟结构的动力响应,结构质量分布于各质点,质点内力则通过质点间的单元来计算并集成。求解过程包括质点全位移、节点纯变形和节点内力计算,详细推导参考文献[10]。
(1) 质点全位移
质点受力情况如图1所示,满足运动微分方程:
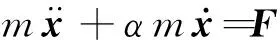
(1)
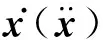
在每个时间步内,采用中央差分公式求解质点运动微分方程(1),得到该时间步末时刻质点的新位置,进而得到该时间步的质点全位移。
(2) 节点纯变形
质点全位移相对应的单元节点全位移包括平移和转动(图2)以及纯变形。为避免刚体位移引起的误差,采用逆向运动进行去除后获得节点纯变形,从而将质点空间运动转换到单元平面上。刚体平移取为参考节点的全位移,刚体转动则通过单元面外和面内的逆向刚体转动矩阵来换算求解。
(3) 节点内力
通过节点纯变形的单元虚功方程来计算节点内力。先引入变形坐标系和单元形函数分布,将空间问题转化到平面上,并以变形坐标系下单元节点的内力向量为坐标轴方向,如图3所示;再利用坐标系转换和面外、面内正向转动,将其转换到整体坐标系下;节点内力反向作用于质点并集成即为质点内力。

图1 质点受力图
Fig.1 Particle force diagram
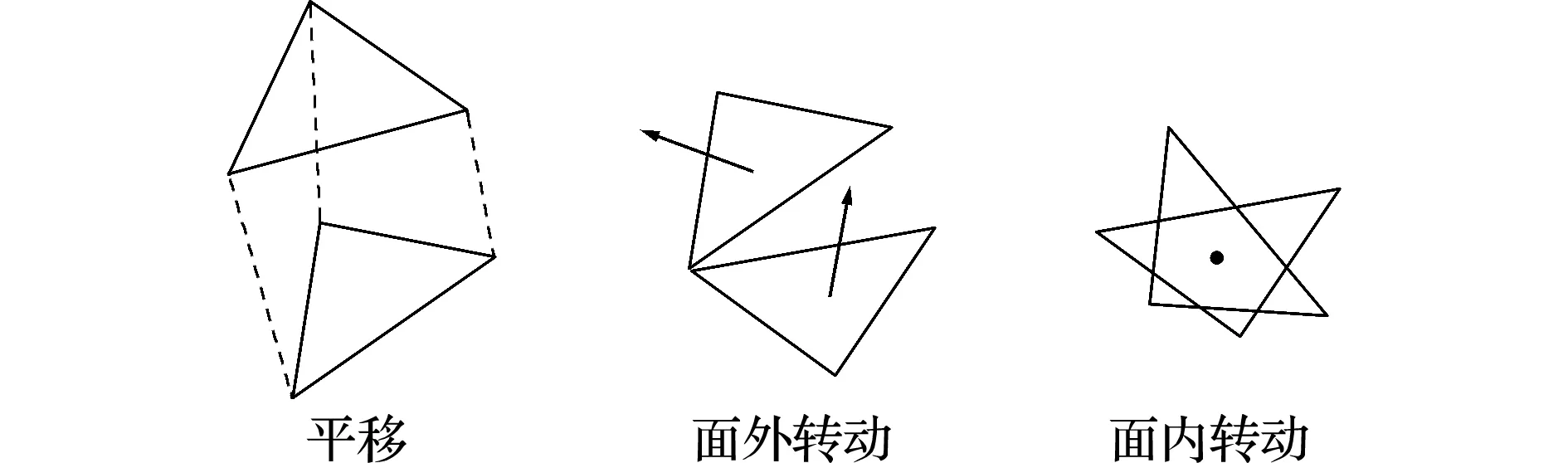
图2 单元的刚体运动
Fig.2 Rigid body motion of element
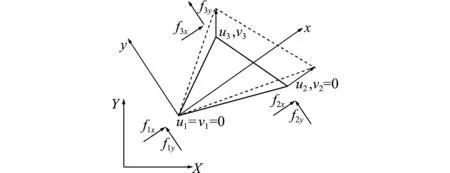
图3 单元节点纯变形和内力
Fig.3 Element node pure deformation and internal force
3 断裂准则及实现
薄膜结构的断裂破坏包括薄膜单元的破裂和破碎情况,本文基于失效应力准则和质点分裂方式来实现薄膜结构的断裂破坏全过程,以下给出了基本原理和推导过程。
采用von Mises应力瞬时变量达到失效应力限值作为膜材单元的断裂失效判据,见式(2)。薄膜单元的向量式有限元基本断裂过程即可通过该断裂判据来完成。
(断裂失效) (2)
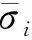
断裂行为是通过质点分裂方式使得相连单元的对应节点断开连接,断裂前后的相关变量如下。
(1) 单元节点的von Mises应力等状态参量是通过该节点对应单元最近积分点处的状态参量获得,且单元仅在节点处出现断裂。节点Mises应力达到失效应力值时断开连接。
(2) 质点分裂形成的新质点属性根据断裂后情况进行重新定义。质点质量m根据断裂后新的单元连接进行重分配;断裂后新质点的位移x和速度v则取保持断裂前质点状态不变。
以质点相连单元中仅一个单元断开为例,质点分裂示意如图4所示,其中E1~E4为单元编号,N1和Ni(i=2,3)分别为分裂前和分裂后的质点编号。质点分裂前后各质点的状态变量满足
(3)
式中x1和v1为分裂前的质点位移和速度,xi和vi(i=2,3)为分裂后的质点位移和速度。
(3) 单元的节点断开方式包括部分断开和所有节点断开,前者一般先出现,对应为单元的破裂行为,后者则对应单元的破碎行为。
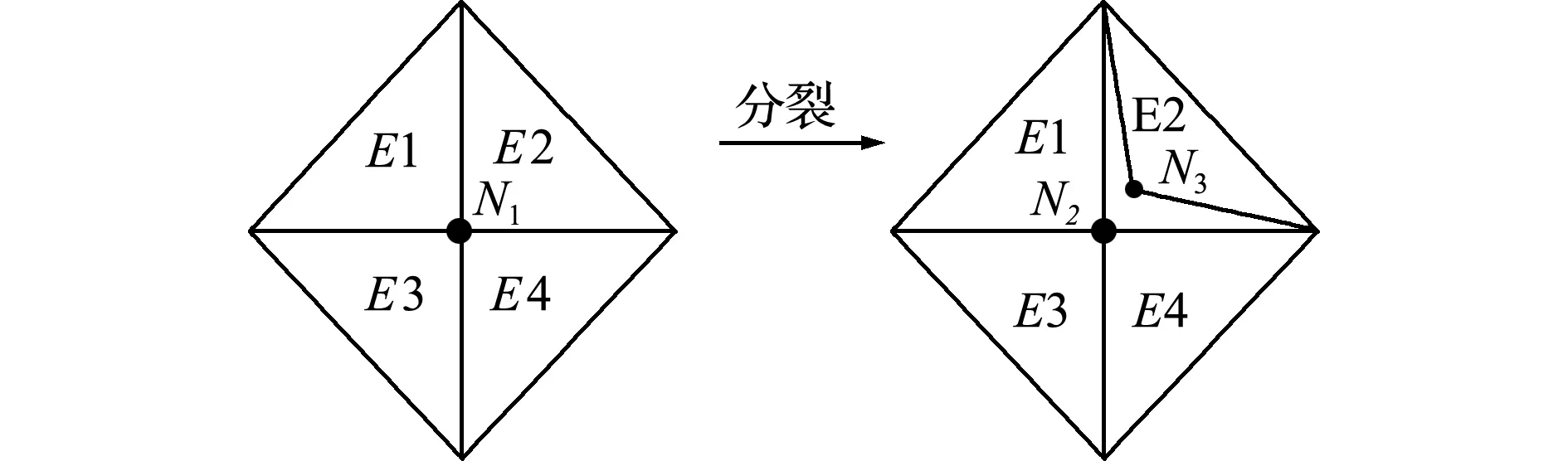
图4 质点分裂示意图
Fig.4 Particle splitting schematic diagram
4 穿透行为实现
膜结构的穿透破坏行为同时结合了碰撞和断裂情况,在每个循环分析子步中,首先出现碰撞检测并进行碰撞响应,接着通过断裂判据来判断断裂的出现情况,并通过质点分裂来实现断裂模拟,跟踪获得膜材变形及穿透破坏的过程。
碰撞检测通过质点和三角形单元的点-三角形碰撞检测方法来处理,碰撞响应则基于结合中央差分与罚函数的碰撞接触反力来实现。时间子步中,首先通过中央差分运动方程求解步末的质点新位移;接着对质点进行碰撞检测处理,对其中发生实际碰撞的质点新位置通过响应处理来更新替换。薄膜结构碰撞接触的推导过程参考文献[11]。
采用von Mises应力状态变量达到失效应力限值作为膜材断裂失效判据,而薄膜结构的断裂行为则通过质点分裂方式,将各相连单元对应节点进行断开操作。单元部分节点断开和单元所有节点断开对应为破裂和破碎过程。
5 程序实现
在进行结构分析计算时,传统有限元需事先区分类型(如断裂及碰撞等)并采用专用的公式和程序来实现,在结构的复杂不连续领域应用不便。向量式有限元对各类复杂不连续力学行为均可采用相同概念和流程实现,即用一个完整而通用的理论进行广义的结构模拟和行为预测。对于结构断裂和穿透问题,只需在基于统一牛顿运动方程的主分析程序中,前者引入断裂失效准则和质点分裂实现模块,后者同时引入碰撞和断裂机制模块;在不增加计算难度和大量计算工作的基础上,通过结构构形的步步更新可跟踪获得其变形、断裂及穿透破坏全过程。
本文采用Matlab编制了薄膜结构的断裂和穿透求解计算程序,并进行了算例分析验证,表明了理论和程序的可靠性和有效性,实现流程如图5所示。
6 算例分析
图7给出了几个典型时刻含裂缝矩形膜片的拉伸变形和膜材撕裂。可以看出,随着拉伸位移Ux的递增,在t=0.6 ms时首先在膜片两侧出现拉伸变形和应力;接着拉伸变形和应力逐渐往中间区域扩展,在t=1.2 ms时膜片中间区域达到较大变形和应力,并在裂缝端部开始出现应力集中效应;在t=1.6 ms时,在裂缝端部由于拉伸变形和应力继续增大而使其Mises应力达到断裂失效应力并开始出现破裂现象;随后,膜片沿着裂缝方向的破裂范围逐渐扩大,即发生撕裂现象(t=2.0 ms,t=2.4 ms);在t=2.8 ms时,矩形膜片出现完全撕裂。

图5 断裂和穿透分析流程图
Fig.5 Fracture and penetration analysis flow chart

图6 矩形膜片模型
Fig.6 Rectangular membrane model



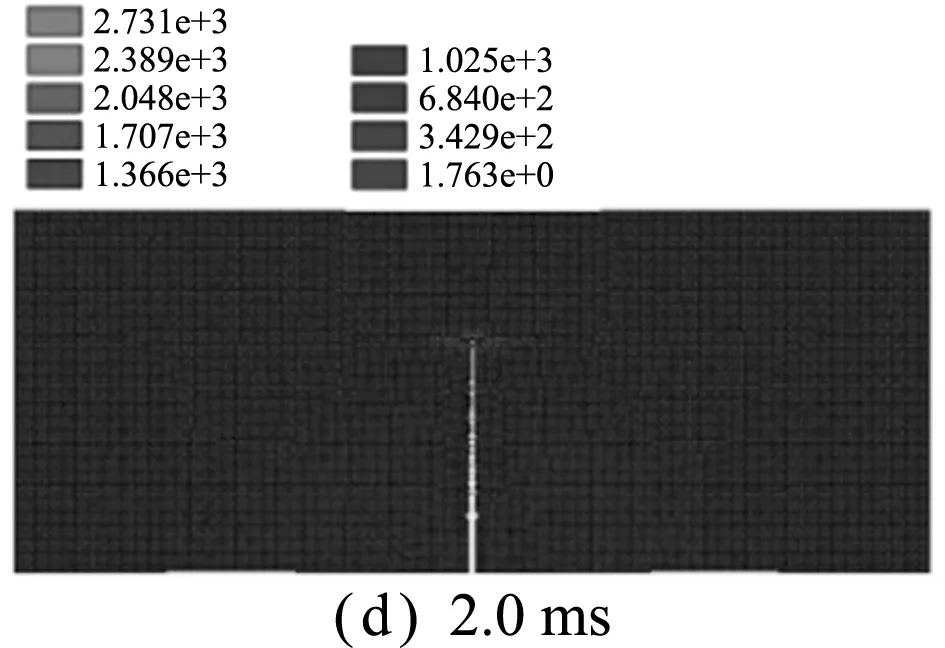


图7 矩形膜片拉伸撕裂典型应力变形图
Fig.7 Typical stress and deformation diagrams of tensile tear for rectangular membrane
本算例矩形膜片的断裂破坏过程与文献[2]的试验结果基本一致,验证了本文方法在薄膜结构断裂行为模拟中的有效性。由于仅采用了简单的Mises应力断裂准则且并未考虑各向异性,与试验结果的定量分析比较还需进一步研究。

图9给出了几个典型时刻方形气囊膨胀直至断裂破坏的变形图。可以看出,随着内压p的增大,t=0.02 s 时,首先在气囊周边出现膨胀变形;继而往中间区域变形扩展,在t=0.05 s时,整个气囊均已充满气并膨胀起;在t=0.06 s时,气囊中心区域由于von Mises应力达到失效应力阈值而开始出现破裂;在t=0.07 s 时,气囊破裂往周边大范围扩展,并开始出现破碎;随后,膜材的破裂破碎变化区域明显,并大范围扩展(t=0.08 s)。
本例采用了简单的Mises失效应力判断准则,并未涉及膜材各向异性及气囊膨胀破裂后气体泄漏引起的内压降低问题,因而气囊膨胀破裂变形与实际情况有所差异。尽管如此,气囊出现断裂的位置及发展模式均基本符合实际情况,证明本文方法可有效模拟薄膜结构的断裂仿真过程。

图8 气囊模型
Fig.8 Airbag model


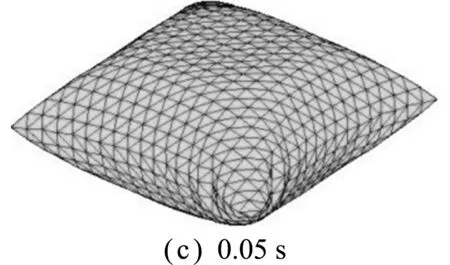



图9 气囊膨胀破裂典型变形图
Fig.9 Typical deformation diagrams of airbag inflating rupture

图11给出了几个典型时刻马鞍面薄膜的穿透变形图。可以看出,首先薄膜在碰撞位置出现凹陷;随着凹陷增大,单元节点应力也增大,直至达到失效应力并开始节点分裂;然后,薄膜在碰撞位置区域沿着最小应力方向(经向)呈现撕裂效果;最终,撕裂趋于明显,刚球逐渐穿透薄膜结构。本算例中马鞍面薄膜的穿透破坏过程与实际情况基本一致,验证了本文方法在薄膜结构穿透行为模拟中的有效性。

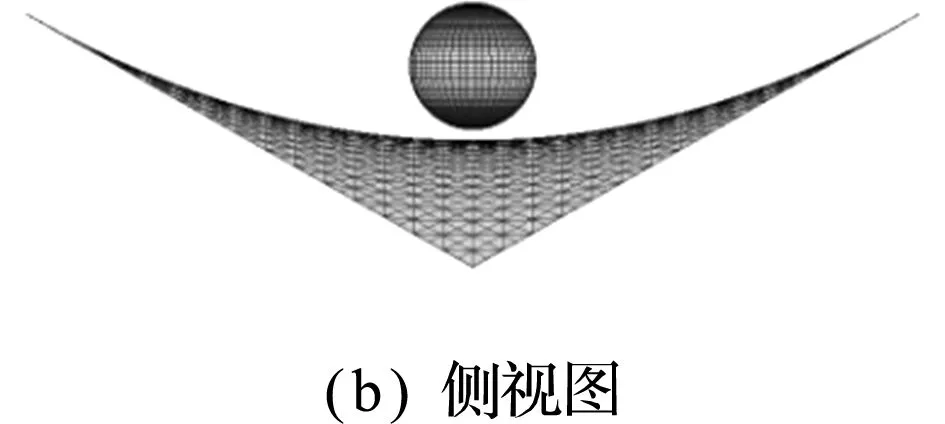
图10 刚球-马鞍面薄膜模型
Fig.10 Rigid ball-saddle membrane model
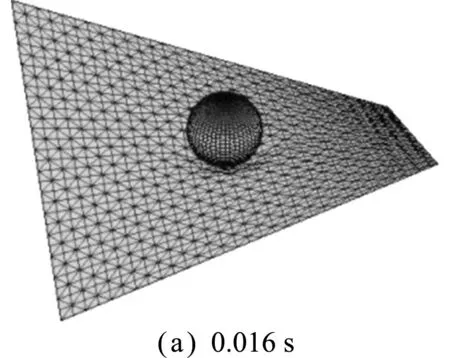
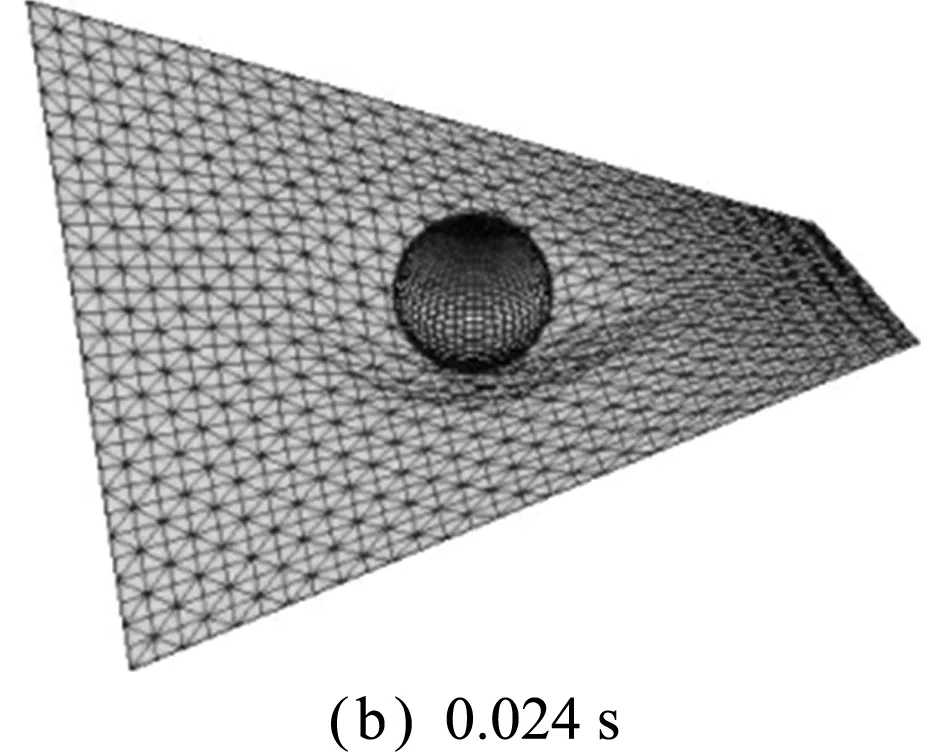
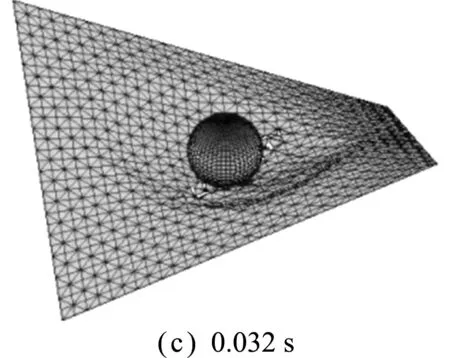
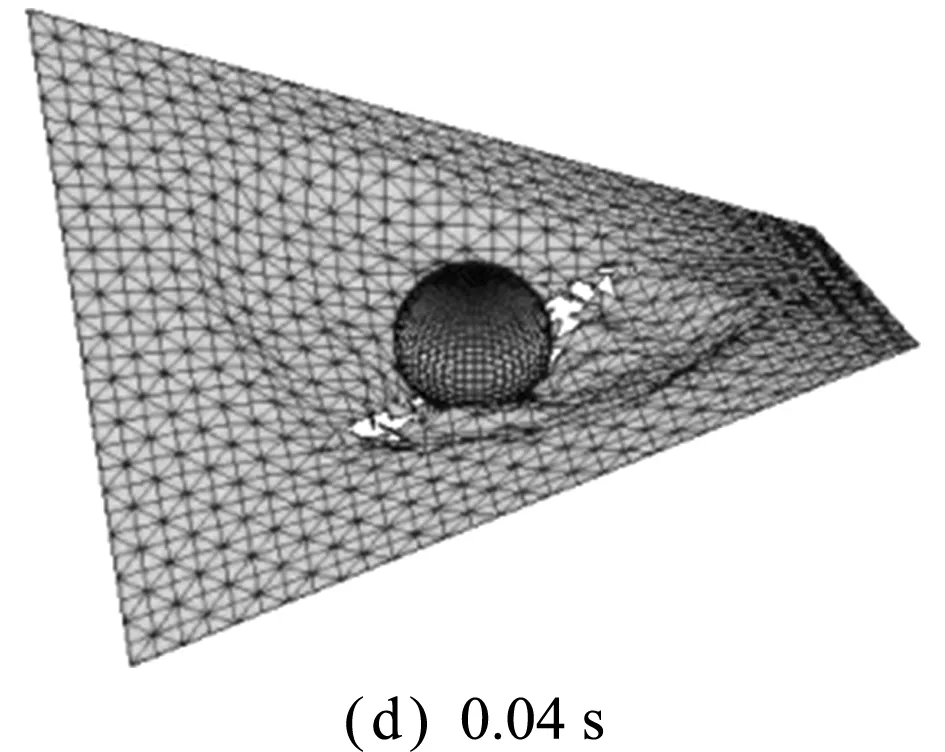

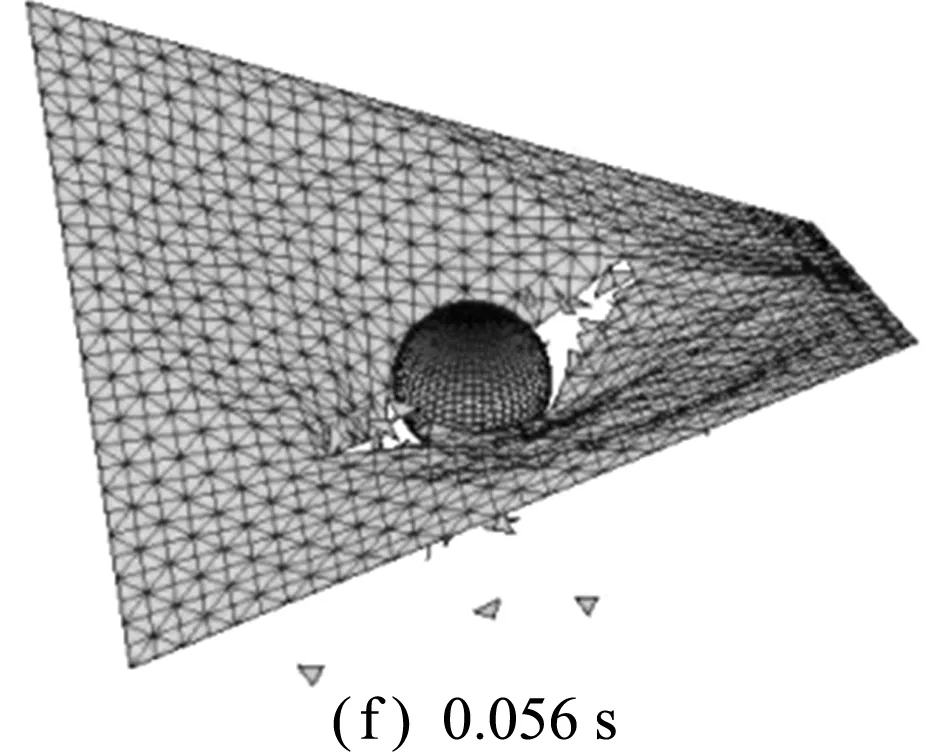
图11 刚球-马鞍面薄膜穿透典型变形图
Fig.11 Typical deformation diagrams of rigid ball-saddle membrane penetration
7 结 论
本文将向量式有限元法引入薄膜结构的断裂和穿透过程分析。提出了膜材的断裂失效应力判据和质点分裂实现方式,模拟获得了薄膜变形和断裂失效全过程;结合碰撞检测和响应机制、断裂失效和向量式实现机制,模拟获得了薄膜变形和穿透破坏全过程。
编制了薄膜结构断裂和穿透求解计算程序,并进行了算例验证。结果表明,该程序可较好完成薄膜结构的大变形大转动、断裂及穿透等复杂不连续行为分析,验证了理论和程序的可靠性和有效性。
本文仅对薄膜结构的断裂及穿透过程进行了基本的模拟分析,要精确实现膜材断裂和穿透这一高度非线性问题需要后续进一步的研究,如各向异性材料的引入、断裂机制的完善和碰撞摩擦的考虑等。
:
[1] 武 岳,胥传喜.膜结构设计(3)——膜结构的荷载态分析与结构设计[J].工业建筑,2004,34(8):73-77.(WU Yue,XU Chuan-xi.Structural analysis and design of membrane structures [J].IndustrialConstruction,2004,34(8):73-77.(in Chinese))
[2] 吴明儿,戴 璐,慕 仝.ePTFE膜材力学性能试验研究[J].建筑材料学报,2010,13(5):632-635.(WU Ming-er,DAI Lu,MU Tong.Experimental studies on mechanical properties of ePTFE fabric [J].JournalofBuildingMaterials,2010,13(5):632-635.(in Chinese))
[3] 陈国华.机织物拉伸断裂过程模拟及强度预测[D].东华大学,2006.(CHEN Guo -hua.The Tensile Breaking Progress Simulation and Strength Prediction of Woven Fabric [D].Donghua University,2006.(in Chinese))
[4] Aldrich-Smith G,Jennett N,Housden J.Adhesion of thin coatings:the VAMAS (TWA 22-2) inter laboratory exercise [J].SurfaceandCoatingsTechno-logy,2005,197(2-3):336-344.
[5] 杨班权,李 朋.残余应力作用下脆性膜/基材料的断裂行为[J].装甲兵工程学院学报,2011,25(1):88-91.(YANG Ban-quan,LI Peng.Fracture behavior of a brittle thin film / substrate system under residual stress [J].JournalofAcademyofArmoredForceEngineering,2011,25(1):88-91.(in Chinese))
[6] 宋维举.薄膜结构在冲击荷载作用下的动力响应研究[D].重庆大学,2011.(SONG Wei-ju.Study on Dynamic Response of Orthotropic Membranes under Impact Loading [D].Chongqing University,2011.(in Chinese))
[7] Ting E C,Shih C,Wang Y K.Fundamentals of a vector form intrinsic finite element (Part I) basic procedure and a plane frame element [J].JournalofMechanics,2004,20(2):113-122.
[8] Ting E C,Shih C,Wang Y K.Fundamentals of a vector form intrinsic finite element (Part II) plane solid elements [J].JournalofMechanics,2004,20(2):123-132.
[9] Ting E C,Shih C,Wang Y K.Fundamentals of a vector form intrinsic finite element (Part III) convected material frame and examples [J].JournalofMechanics,2004,20(2):113-123.
[10] 赵 阳,王 震,彭 涛.向量式有限元膜单元及其在膜结构褶皱分析中的应用[J].建筑结构学报,2015,36(1):127-135.(ZHAO Yang,WANG Zhen,PENG Tao.Membrane element based on vector form intrinsic finite element and its application in wrinkling ana-lysis of membrane structures [J].JournalofBuil-dingStructures,2015,36(1):127-135.(in Chinese))
[11] 王 震,赵 阳.膜材碰撞接触分析的向量式有限元法[J].计算力学学报,2014,31(3):378-383.(WANG Zhen,ZHAO Yang.Vector Form Intrinsic Finite Element method for collision-contact analysis of membrane material [J].ChineseJournalofComputa-tionalMechanics,2014,31(3):378-383.(in Chinese))

