考虑质量变化的刚架结构损伤识别方法研究
,
(清华大学 土木工程系,北京 100084)
1 引 言
结构在服役期间都会存在一定程度的损伤,严重时将导致结构倒塌等灾难性事故。因此,对工程结构损伤识别的研究已迅速成为土木工程领域关注的热点问题[1-3]。
Shi等[4,5]通过单元模态应变能改变率指标对结构损伤进行定位,并基于振型扩充技术,利用模态应变能灵敏度矩阵对结构损伤进行定量分析。Hu等[6,7]提出的交叉模态应变能法充分利用了测量模态和理论模态信息,无需迭代,仅需少量的测量模态即可对结构损伤进行准确的识别。Seyedpoor[8]利用相对模态应变能构造的指标进行损伤定位,之后通过粒子群优化算法对构建的目标函数进行优化求解来确定结构损伤程度。Hsu等[9]结合频率和模态应变能灵敏度矩阵构建损伤定量分析方程,依据不同的截面特性(拉压、抗弯和抗扭)对梁单元的刚度矩阵进行分解,在此基础上对分解后每一部分的单元刚度对应的损伤指标进行识别。
刚架结构基本单元为梁单元,现有研究在对刚架结构进行分析时,通常以折减单元刚度来对结构损伤进行模拟[4-8,10,11],并假设结构损伤前后质量保持不变。但对于结构单元出现缺口这类损伤时,更为合理的损伤模拟方法为折减损伤单元截面积。截面积变化对单元不同截面特性(拉压、抗弯和抗扭)的影响并不一致,所以无法通过一个统一的指标来描述单元损伤。因此,在前人研究的基础上[9],考虑单元截面积减小带来的结构质量变化,在此基础上推导损伤定量分析方程。之后,对单元刚度矩阵进行分解,以多个损伤指标描述单元损伤,并通过最小二乘算法求解损伤指标。最后以算例验证了本文所提方法对钢结构损伤识别的有效性。
2 理论背景
模态应变能方法利用结构损伤前后模态振型和结构刚度矩阵的信息进行损伤识别。其中相对模态应变能指标对结构局部损伤敏感度高,能精确地对结构损伤进行定位。
本节对相对模态应变能方法做简要回顾。结构损伤前后的单元模态应变能为[4]
(1,2)
式中Ui j和Udi j分别为损伤前后单元j的第i阶模态应变能,Φi和Φdi分别为损伤前后第i阶模态振型,Kj和Kdj分别为损伤前后单元j的刚度矩阵。由于损伤后单元j的刚度矩阵未知,本文采用损伤前的单元刚度矩阵Kj代替Kdj进行计算。
损伤前后整个结构第i阶模态总的应变能由所有单元的模态应变能求和得到,可表示为
(3,4)
式中K和Kd分别为完好结构和损伤结构的整体刚度矩阵,类似地,计算时用K来代替Kd。根据上式可以定义结构损伤前后单元相对模态应变能为
(5)
FUdi j=Udi j/Udi=ΦdTiKjΦdi/(ΦdTiKΦdi)
(6)
为了降低噪声对模态振型的影响,选用前m阶模态计算单元相对模态应变能指标:
(7)
损伤前后结构无阻尼自由振动的特征方程为
(8,9)
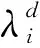
结构损伤引起损伤单元截面积的减小,从而导致结构刚度矩阵和质量矩阵发生变化,即
(10)
(11)
式中αj和βj分别为损伤单元的刚度和质量对应的损伤系数,其取值区间为[0,1],Nd为结构损伤单元总数,Mj为单元j的质量矩阵,本文采用一致质量矩阵。
(12)
(13)
将式(10,11)代入式(13)得
(14)
由式(12,14),结合结构刚度矩阵K和质量矩阵M的对称性可得
(15)
将式(10,11)代入式(15)得
(16)
式中i=1,2,…,n;r=1,2,…,m。其中n和m分别为完好结构和损伤结构可获取的模态数目,方程总数记为Nq=n×m。
将式(16)写成矩阵形式为
{SK,SM}{α,β}=R
(17)
式中
(18a)
(18b)
(18c)
记S={SK,SM},d={α,β},式(17)可写为
Sd=R
(19)
式中S为Nq×2Nd维矩阵,d为2Nd×1维向量,R为Nq×1维向量。
梁单元不同于杆单元,损伤单元截面积减小引起不同截面特性(拉压、抗弯和抗扭)的变化程度不一致。因此,根据其截面特性对单元刚度矩阵进行分解。损伤前后单元j的刚度矩阵变化为[9]
(20)
式中 上标A为截面积A对应的拉压部分以及相应的损伤系数,Iz和Iy分别为z轴和y轴对应的弯曲惯性矩,Ix为x轴的扭转惯性矩。
将单元刚度矩阵分解后,单元j刚度矩阵对应的损伤系数αj拓展为
(21)
将式(20,21)代入式(16)得
(22)
写成矩阵形式为
{SK A,SK I z,SK I y,SK I x,SM}×{αA,αI z,αI y,αI x,β}=R
(23)
式中
(24a,24b)
(24c,24d)
类似地,式(19)可改写为
S*d*=R
(25)
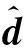
(26)
3 算例分析
以一个二维刚架结构作为算例验证本文所提方法,分析时不考虑结构的平面外弯曲以及结构的扭转。因此,单元刚度矩阵只包含轴向变形和平面内弯曲两部分。

(27)
(28)

选择三种损伤工况进行算例分析。工况1为竖直方向单元8发生损伤,工况2为水平方向单元10发生损伤,工况3为单元8和10同时发生损伤,具体工况列入表1。
对于平面刚架单元,每个节点位移包含轴向位移、横向位移以及平面内的转角三个部分,其单元的刚度矩阵和质量矩阵由式(29,30)计算三种工况的损伤定位结果如图2~图4所示。可以看出,三种工况下,损伤位置处损伤定位指标FUCR的值明显大于其他位置,因此可以判断工况1的损伤单元为单元8,工况2的损伤单元为单元10,工况3的损伤单元为单元8和10。此外,施加的5%振型噪声对损伤定位指标FUCR值的影响很小。以上结果说明,该指标具有良好的损伤定位能力和抗噪性。
(29)
(30)
表1 刚架结构损伤工况
Tab.1 Damage cases of frame structure

损伤工况损伤单元截面损伤截面积减小惯性矩减小质量减小工况18高h减小20%20%48.8%20%工况210高h减小20%20%48.8%20%工况38高h减小20%20%48.8%20%10高h减小30%30%65.7%30%
(1) 结构质量变化的影响

(31)
式中So r i={SK A,SK I z,SK I y,SK I x}。

图1 平面刚架有限元模型
Fig.1 FEM of a planar rigid frame

图2 工况1的损伤定位结果
Fig.2 Damage localization results of case 1
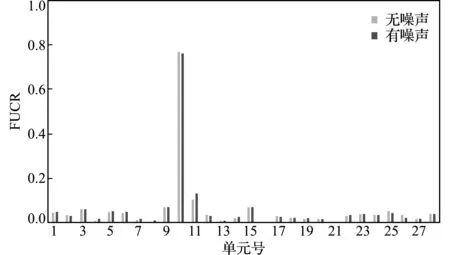
图3 工况2的损伤定位结果
Fig.3 Damage localization results of case 2
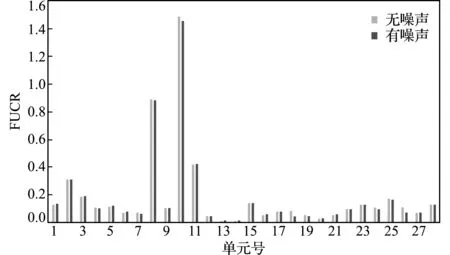
图4 工况3的损伤定位结果
Fig.4 Damage localization results of case 3
(2) 噪声的影响
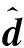

表2 刚架结构损伤程度识别结果Tab.2 Damage quantification results of rigid frame structure
4 结 语
本文以单元截面积的折减定义刚架结构单元损伤,考虑结构损伤带来的质量变化,在此基础上提出了一种考虑质量损失的刚架结构的损伤识别方法。主要结论如下。
(1) 本文使用的相对模态应变能指标能够对刚架结构损伤进行准确定位,且具有较强的抗噪能力。
(2) 在对单元刚度矩阵进行分解的前提下,以多个指标对单元损伤进行描述,这些指标对应的物理意义更加明确,可以更好地反映单元实际的损伤情况。
(3) 本文方法能准确识别刚架结构单损伤和多损伤工况下损伤单元的损伤程度。噪声存在时虽然使得部分指标失效,但综合考虑其他指标的识别结果仍可以判断单元的损伤程度。
:
[1] Fan W,Qiao P.Vibration-based damage identification methods:a review and comparative study[J].StructuralHealthMonitoring,2011,10(1):83-111.
[2] Sung S H,Jung H J,Jung H Y.Damage detection for beam-like structures using the normalized curvature of a uniform load surface[J].JournalofSoundandVibration,2013,332(6):1501-1519.
[3] Cha Y J,Buyukozturk O.Structural damage detection using modal strain energy and hybrid multiobjective optimization[J].Computer-AidedCivilandInfrastructureEngineering,2015,30(5):347-358.
[4] Shi Z Y,Law S S,Zhang L M.Structural damage detection from modal strain energy change[J].JournalofEngineeringMechanics,2000,126(12):1216-1223.
[5] Shi Z Y,Law S S,Zhang L M.Improved damage quantification from elemental modal strain energy change[J].JournalofEngineeringMechanics,2002,128(5):521-529.
[6] Hu S L J,Wang S,Li H.Cross-Modal Strain energy method for estimating damage severity[J].JournalofEngineeringMechanics,2006,132(4):429-437.
[7] Li H,Fang H,Hu S L J.Damage localization and severity estimate for three -dimensional frame structures[J].JournalofSoundandVibration,2007,301(3):481-494.
[8] Seyedpoor S M.A two stage method for structural damage detection using a modal strain energy based index and particle swarm optimization[J].InternationalJournalofNon-LinearMechanics,2012,47(1):1-8.
[9] Hsu T Y,Loh C H.Damage diagnosis of frame structures using modified modal strain energy change method[J].JournalofEngineeringMechanics,2008,134(11) :1000-1012.
[10] Moradipour P,Chan T H T,Gallag C.An improved modal strain energy method for structural damage detection,2D simulation[J].StructuralEngineeringandMechanics,2015,54(1):105-119.
[11] 曹永红,张新亮,曹 辉,等.基于实用完备模态空间的两阶段损伤识别方案[J].工程力学,2009,26(3):168-175.(CAO Yong-hong,ZHANG Xin-liang,CAO Hui,et al.Two -stage damage identification schbaemseed on practical complete modal space [J].EngineeringMechanics,2009,26(3):168-175.(in Chinese))
[12] 郑 飞,许金余.基于缩聚模态应变能与频率的结构损伤识别[J].工程力学,2012,29(7):117-123.(ZHENG Fei,XU Jin-yu.Structural damage dection based on reduced modal strain energy and Frequency [J].EngineeringMechanics,2012,29(7):117-123.(in Chinese))

