碳纳米管增强型复合材料功能梯度板的自由振动模型与尺度效应
,
(沈阳航空航天大学 辽宁省飞行器复合材料结构分析与仿真重点实验室,沈阳 110136)
1 引 言
碳纳米管(CNTs)具有高强度、高刚度、低密度以及良好的延展性[1]等优点,可用作复合材料的增强相。研究表明,很低的CNTs含量就可以极大提高CNTs增强复合材料的力学性能[2]。当CNTs在基体材料中遵循某种特定规律呈梯度分布时就形成了CNTs增强型功能梯度复合材料(FG-CNTRC)。随着微/纳米机电技术的发展,FG-CNTRC已经广泛应用于微/纳米级别的传感器、制动器以及显微镜等[3]。
诸多试验已经证实,当结构的几何尺寸接近微米量级时,材料将表现出比宏观状态下更高的刚度,即尺度效应[4]。传统连续介质力学理论无法描述这种现象,因此发展了能够解释尺度效应的应变梯度理论[5]和偶应力理论[6]。这两种理论都在本构关系中引入了若干个和尺度效应有关的尺度参数。
Yang等[7]提出了只含有一个尺度参数且适用于各向同性材料的修正偶应力理论。近年来,基于该理论建立了一系列板和梁模型[8,9]。随后,陈万吉等[10]提出了一种能够适用于各向异性材料的新修正偶应力理论,并基于该理论建立了各向异性的微/纳观复合材料层合梁及层合板模型[10-12]。
当较长的CNTs在基体中沿特定方向排列时,FG -CNTRC 可作为各向异性材料。Shahriari等[13]基于应变梯度理论较早建立了各向异性 FG -CNTRC 板的自由振动模型。目前基于偶应力理论的各向异性 FG-CNTRC 板的研究尚属空白。
本文基于修正偶应力理论,建立了只含有一个尺度参数的各向异性 FG -CNTRC 板的自由振动模型。基于哈密顿原理推导了运动微分方程,并以四边简支板为例对板自由振动频率进行了计算。
2 新修正偶应力理论

(1)
式中u和ω分别为平动位移和转动位移。该理论下的本构关系定义为
(2)
式中δ是克罗内克符号,λ和G是Lame常数,σi j为正应力,mi j为偶应力,li是材料尺度参数。下标i和j均为自由指标。
3 FG -CNTRC 板的基本方程
薄板或中厚板的横向变形和翘曲变形很小,可采用Mindlin板理论对位移进行描述:
(3)
式中u0和v0分别为板中性面沿x轴方向和y轴方向的位移,Ψx和Ψy分别为板绕y轴和x轴的转角。
板的转动位移由公式ωi=1/2ei j kuk,j得到(本文假设转动位移ωz=0[12])。由式(1)可进一步得到应变分量和曲率分量。
本构关系表示为
σ=Qε
(4)
式中σ和ε分别为应力和应变,Q为刚度矩阵。
Q11=E11/(1-υ12υ21),Q12=υ21E11/(1-υ12υ21)
Q22=E22/(1-υ12υ21),Q33=G12,Q44=G13
Q55=G23,Q66=G13,Q77=G23,G12=G13=G23
lb和lm分别为CNTs和基体材料的尺度参数。E11和E22分别为板沿CNTs和垂直于CNTs方向的弹性模量,G12,G13和G23为板的剪切模量,υ12和υ21为泊松比,且有[14]
(5)
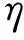
横观各向同性截面内的纤维(断面)可以看成是夹杂,该夹杂的尺寸远大于横观各向异性截面内的纤维和基体的夹杂尺度。因此,CNTs的尺度参数lb远大于基体的尺度参数lm,为了便于工程应用,可近似认为lm=0,即只需一个尺度参数。
本文考虑CNTs的四种分布方式[14]
(6)
式中z为沿板厚的坐标值,以板厚中性面为z=0的面。
4 FG -CNTRC 板的运动方程
FG -CNTRC 板的哈密顿原理表示为
(7)
式中U为应变势能,W为外力功,T为动能,t1和t2表示时间,
(8)
(9)
(10)
(11)

将式(8~10)代入式(7)可得板的运动微分方程为
(12)
边界条件为
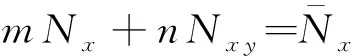


电视画面中的字幕发布了首相的指示:“你们中的许多人都安全地聚集在学校礼堂和社区中心里。我们要求你们待在原地,这样你们能得到处理。假如你们待在家中,请待在原地;我们会找到你。”


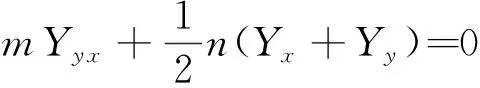

(13)

5 算例分析
简支板的边界条件为

at edgex=0,a

at edgey=0,b
(14)
位移试函数设为
(15)
式中α=π/a,β=π/b。u00,v00,Ψx0,Ψy0和w0为待定系数,ω为待求频率。a和b分别为板沿CNTs和垂直于CNTs方向的长度。
将式(15)代入运动微分方程(12)得到
([K]-ω2[M]){U}=0
(16)
式中 {U}={u00v00Ψx0Ψy0w0}T,[K]和[M]分别为刚度矩阵和质量矩阵。对式(16)求广义特征值便可得到板的自振频率。计算过程中引入剪切修正系数[14]:
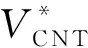
(17)
FG -CNTRC 的材料常数及CNTs效率参数分别列入表1和表2[14]。

表2 CNTs的效率参数
Tab.2 CNTs efficiency parameters
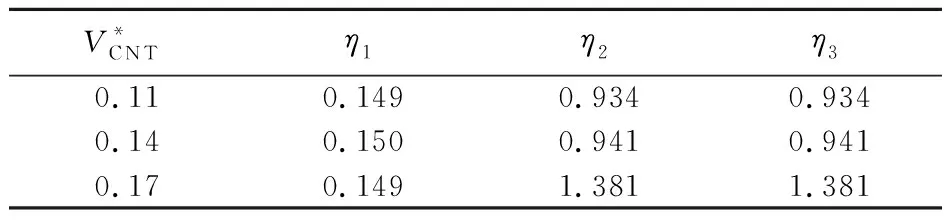
V*CNTη1η2η30.110.1490.9340.9340.140.1500.9410.9410.170.1491.3811.381
算例1可靠性验证

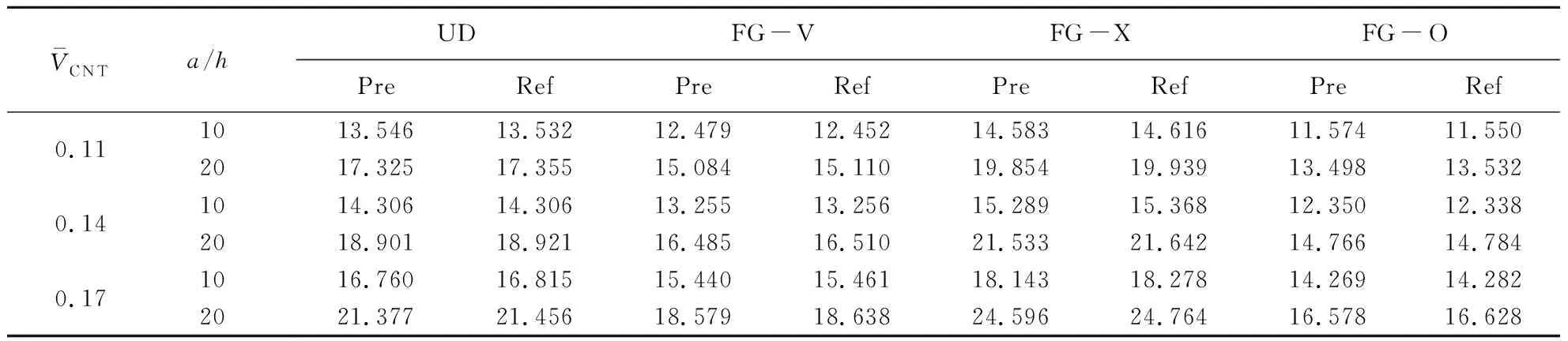
表3 本文模型得到的自振频率与文献对比Tab.3 Comparison of the dimensionless fundamental frequency of the FG -CNTRC plate
算例2尺度效应对自振频率的影响
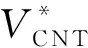
图1中present为本文模型解,classical为经典弹性理论的Mindlin板模型解。可以看出,本文模型所预测的板的自振频率总是高于经典弹性理论的Mindlin板模型的计算结果,且两者之间的差别随着板厚与尺度参数比值的增大而减小。说明本文模型能够有效地描述尺度效应对结构刚度的影响,且板的尺寸越小,尺度效应对结构刚度的增强效果越明显,而随着板的几何尺寸逐渐增大时,尺度效应逐渐消失。
算例3碳纳米管体分比对板自振频率的影响
以 FG -X 型分布为例,研究CNTs体分比分别取0.11,0.14和0.17时 FG -CNTRC 板的自振频率,预测结果如图2所示。固定板长和板厚,h=l=17.6 μm,a=10 h,无量纲化处理方式同算例2。
图1 不同厚度的方板自振频率
Fig.1 Natural frequencies of square plates with different thickness

图2 不同碳纳米管体积分数下的无量纲频率
Fig.2 Dimensionless frequencies with different volume fraction of carbon nanotubes
图中横坐标为板的长宽比a/b,纵坐标为无量纲自振频率。可以看出,CNTs体分比越高,板的自振频率越大。说明CNTs可以提高结构刚度,且CNTs体积分数越高结构的刚度越大。
算例4碳纳米管分布方式对自振频率的影响
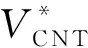

图3 不同碳纳米管分布方式的无量纲频率
Fig.3 Dimensionless frequencies with differentdistribution of carbon nanotubes
6 结 论
本文基于一种新的修正偶应力理论,建立了CNTs增强复合材料功能梯度板的自由振动模型。该模型预测的板的自振频率总是高于经典弹性理论下Mindlin板模型预测的结果,说明该模型能够有效地描述尺度效应对结构刚度的影响。结构的尺寸越小,尺度效应就越明显,当结构尺寸远大于尺度参数值时,尺度效应消失。CNTs体积分数的增加能够显著提高结构的刚度,而其在基体中的分布形式也对板的刚度有直接影响。
:
[1] Liew K M,Lei Z X,Zhang L W.Mechanical analysis of functionally graded carbon nanotube reinforced composites:a review[J].CompositeStructures,2015,120:90-97.
[2] Wuite J,Adali S.Deflection and stress behaviour of nanocomposite reinforced beams using a multiscale analysis[J].CompositeStructures,2005,71(3):388-396.
[3] Wang W L,Hu S J.Modal response and frequency shift of the cantilever in a noncontact atomic force microscope [J].AppliedPhysicsLetters,2005,87(18):183506.
[4] Stölken J S,Evans A G.A microbend test method for measuring the plasticity length scale [J].ActaMaterialia.1998,46(14):5109-5115.
[5] Fleck N A,Hutchinson J W.Strain gradient plasticity[J].AdvancesinAppliedMechanics,1997,33:295-361.
[6] Toupin R A.Theories of elasticity with couple -stress[J].ArchiveforRationalMechanicsandAnalysis,1964,17(2):85-112.
[7] Yang F,Chong A C M,Lam D C C,et al.Couple stress based strain gradient theory for elasticity[J].InternationalJournalofSolidsandStructures,2002,39(10):2731-2743.
[8] Ma H M,Gao X L,Reddy J N.A non-classical Mindlin plate model based on a modified couple stress theory[J].ActaMechanica,2011,220(14):217-235.
[9] Ma H M,Gao X L,Reddy J N.A nonclassical Reddy-Levinson beam model based on a modified couple stress theory[J].InternationalJournalforMultiscaleComputationalEngineering,2010,8(2):167-180.
[10] Chen W J,Li L,Xu M.A modified couple stress model for bending analysis of composite laminated beams with first order shear deformation [J].CompositeStructures,2011,93(11):2723-2732.
[11] 贺 丹,杨万里,陈万吉.基于各向异性修正偶应力理论的Reddy型层合板的自由振动[J].固体力学学报,2016,37(2):161-171.(HE Dan,YANG Wan-li,CHEN Wan-ji.Free vibration of composite laminated Reddy plate based on anisotropic modified couple stress theory[J].ChineseJournalofSolidsMecha-nics,2016,37(2):161-171.(in Chinese))
[12] 陈万吉,牛 惠.基于新修正偶应力理论的Mindlin层合板稳定性分析[J].计算力学学报,2016,33(5):717-724.(CHEN Wan-ji,NIU Hui.Buckling analysis of composite laminated Mindlin plate based on new modified couple stress theory[J].ChineseJournalofComputationalMechanics,2016,33(5):717-724.(in Chinese))
[13] Shahriari B,Karamooz R M R,Zeighampour H.Vibration analysis of functionally graded carbon nanotube -reinforced composite nanoplates using Mindlin’s strain gradient theory [J].CompositeStructures,2015,134(5):1036-1043.
[14] Zhu P,Lei Z X,Liew K M.Static and free vibration analyses of carbon nanotube -reinforced composite plates using finite element method with first order shear deformation plate theory[J].CompositeStructures,2012,94(4):1450-1460.
[15] Ke L L,Wang Y S.Size effect on dynamic stability of functionally graded microbeams based on a modified couple stress theory[J].CompositeStructures,2011,93(2):342-350.

