弹性薄板结构的等效激励谱反演问题研究
, *,
(1.山东大学 机械工程学院,济南 250061;2.山东大学 高效洁静机械制造教育部重点实验室,济南 250061)
1 引 言
振动现象的发生通常与激励的存在相关,准确了解激励特性是进行结构振动设计、振动特性分析及振动环境预测等工作的依据。实际问题中,通常难以实现激励的直接测量,根据结构振动响应对其所受激励进行估计的方法得到了广泛应用[1,2],由此发展形成了动载荷识别技术领域[3]。如在舰船岸基维修中,通过测量安装基础的振动响应对振源设备的激励水平进行评估[4],或利用实测未充水的声纳基阵腔壁振动响应估计其所受外部机械激励,并作为声纳部位机械自噪声评估的参考依据[5]。因此,如何提高估算精度、简化测试和估算过程是研究的重点[6-8]。
在许多环境激励评估问题中,实际关注的是激励的平均水平及作用效果预测[9]。本文所探讨的等效激励法(虚拟激励法),是指将作用位置未知的激励虚拟作用于有限数目的参考节点上,基于响应相似原则反演求取具有最小均方幅值的激励分布形式,在机械等力学领域得到广泛应用[10-11]。本文基于弹性薄板结构的振动模态理论,对根据有限振动响应数据估计等效激励谱的一般方法进行了理论分析论证。考虑到实际测试工作的复杂性以及模态和测点选取对结果的影响[12-14],运用简支边矩形薄板的Navier解法研究了等效激励估计实验方案中影响结果可靠性的主要影响模态的选取、测点的数量和选点布局以及等效激励点的数量和位置设置等因素。最后,通过四边固支矩形薄板的有限元法等效激励谱反演算例对相关理论分析进行了验证。
2 弹性薄板结构等效激励反演理论
弹性薄板的振动微分方程为
(1)

设激励f(σ,t)=F(σ)ej ω,根据振型叠加法
(2)
式中ωi,Mi和Ψi分别为板的第i阶模态频率、模态质量和振型函数;ξi为第i阶振型Ψi的模态影响因子;Qi为广义激励。
Qi=∬AF(σ)Ψi(σ)dσ
(3)
(4)
式中x≥1,ε为模态截断误差。
等效激励估计问题主要面向低中频域,故在式(4)中令x=1,选σ1,…,σM为观测点,获取观测值W=[W(σ1ω),…,W(σM,ω)]T,得观测矩阵方程:
W=Ψξ+ε
(5)
式中Ψ=[Ψi j]M ×N,Ψi j=Ψj(σi),ξ=[ξ1,ξ2,…,ξN]T,ε=[ε1,ε2,…,εM]T。
应用最小二乘估计原理,使残差εTε最小的ξ为
ξ=(ΨTΨ)-1·ΨTW
(6)
由式(2)得到主要影响模态的广义激励
Q=M(Ω2-ω2IN)ξ
(7)
式中IN为N阶单位方阵,M=diag[M1,M2,…,MN],Ω=diag[ω1,ω2,…,ωN],Q=[Q1,Q2,…,QN]T。

Q=Ψe qFe q
(8)
式中Ψe q=[Ψi j]N ×L,Ψi j=Ψi(σe q j)。

Fe q=ΨTe q(Ψe qΨTe q)-1Q=ΨTe q(Ψe qΨTe q)-1M(Ω2-
ω2IN)(ΨTΨ)-1ΨTW
(9)
3 等效激励估计影响因素分析
不失一般性地,考虑简支边界矩形薄板,根据 Na-vier解法,其固有频率、振型函数和模态质量分别为
(10)
Ψi(σ)=sin(Miπx/LX)sin(niπy/LY)
(11)

(12)
式中i=1,2,…,(Mi,ni)∈N2,且使ω1<ω2<…;LX和LY为矩形板的边长。
在矩形板上划分网格并对节点编号,如图1所示。设矩形板边长LX=0.6 m,LY=0.4 m,厚度h=0.005 m,材料为45号钢。随机选取节点施加简谐激励,由式(2,3,10~12)可得各阶ωi,Qi,Mi和ξi。


图1 矩形板的网格节点编号和观测点/等效激励点布置
Fig.1 Grid node number and arrangement of observation points/ equivalent excitation points of rectangular plate

图2 500Hz单位简谐激励下的前25阶模态影响因子
Fig.2 First 25 order modal impact factors under unit harmonic force (500 Hz) excitation
(13)
根据上述分析,假设分别取激励频率附近的5,10,15和20阶模态合成1~77号节点的振动响应(幅值为|W(σ)|),结果比较如图3所示。显然,仅取5阶模态将产生显著的模态截断误差,取10,15和20阶的计算结果非常接近,因此必须保证参与计算的主要影响模态的数量不能太少,但亦无需太多。
显然,布置测点的数目越多,越能准确地反映结构的振动模式。在实际操作中应寻求如何以较少的测点数目和较小的测试工作量获取较准确可靠的计算结果。
对图1,若选取激励频率附近的10阶模态作为主要影响模态,应保证观测点数量M≥10。为了研究观测点数量和选点布局对等效激励估计精度的影响,考虑几种不同的观测点选取方案,(1) 取 图1 全部77个节点;(2) 取图1中阴影部分包含的49个节点;(3) 取图1中重叠阴影部分的12个节点;(4) 取图1中点划线框包含的20个节点;(5) 取图1中虚线框包含的20个节点。
设在矩形板上施加一个500 Hz的单位简谐集中力(27号节点),用前25阶振型叠加计算板上1~77号节点的振动位移作为响应观测值;然后,按照上述5种观测点方案构造观测向量W,同时将各测点坐标代入式(5)获得观测点模态矩阵Ψ;最后,由式(6)估算模态影响因子ξ。图4是对5种测点布置方案下的前10阶模态影响因子估算结果的比较。
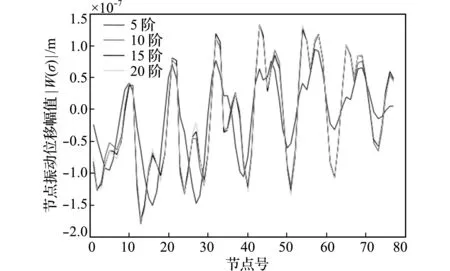
图3 不同阶数模态叠加合成节点位移响应的结果对比
Fig.3 Comparison of node displacement responses resulted from superposition of different numbers of plate’s modes
方案(1)的结果与理论值相近;方案(2)测点数量较多,精度较高;方案(3)选取了12个观测点,观测点规模与方案(1,2)相比大为减小,仍有较高的估计精度;方案(4)的观测点布置过于集中,导致了较大的估算误差;方案(5)的观测点布局畸形集中而导致计算结果奇异,由于该方案结果偏差较大,未在图4中显示。
将上述各模态影响因子代入式(7)即完成了对广义激励的估计,利用式(8)或式(9)进行等效激励估计。由于不存在唯一的等效激励点设置方案,等效激励估计的可靠性通过结构在等效激励作用下的振动响应与实际激励作用效果的近似程度来评价。
为保证式(8)存在等效激励解,必须使L≥N。对图1算例,选取三种等效激励点设置方案,(I) 1,7,10,23,24,27,33,56,57和66号节点;(II) 1,7,10,23,24,29,33,56,57和66号节点;(III) 5,10,11,24,29,45,46,62和68号节点。沿用前文计算结果,根据方案(3)进行等效激励估计,重新应用式(2)预测等效激励振动响应,图5是三种方案的预测效果与实际振动响应的对比。

图4 不同测点布置方案的模态影响因子估计结果对比
Fig.4 Comparison of modal impact factors of different observation points layout schemes
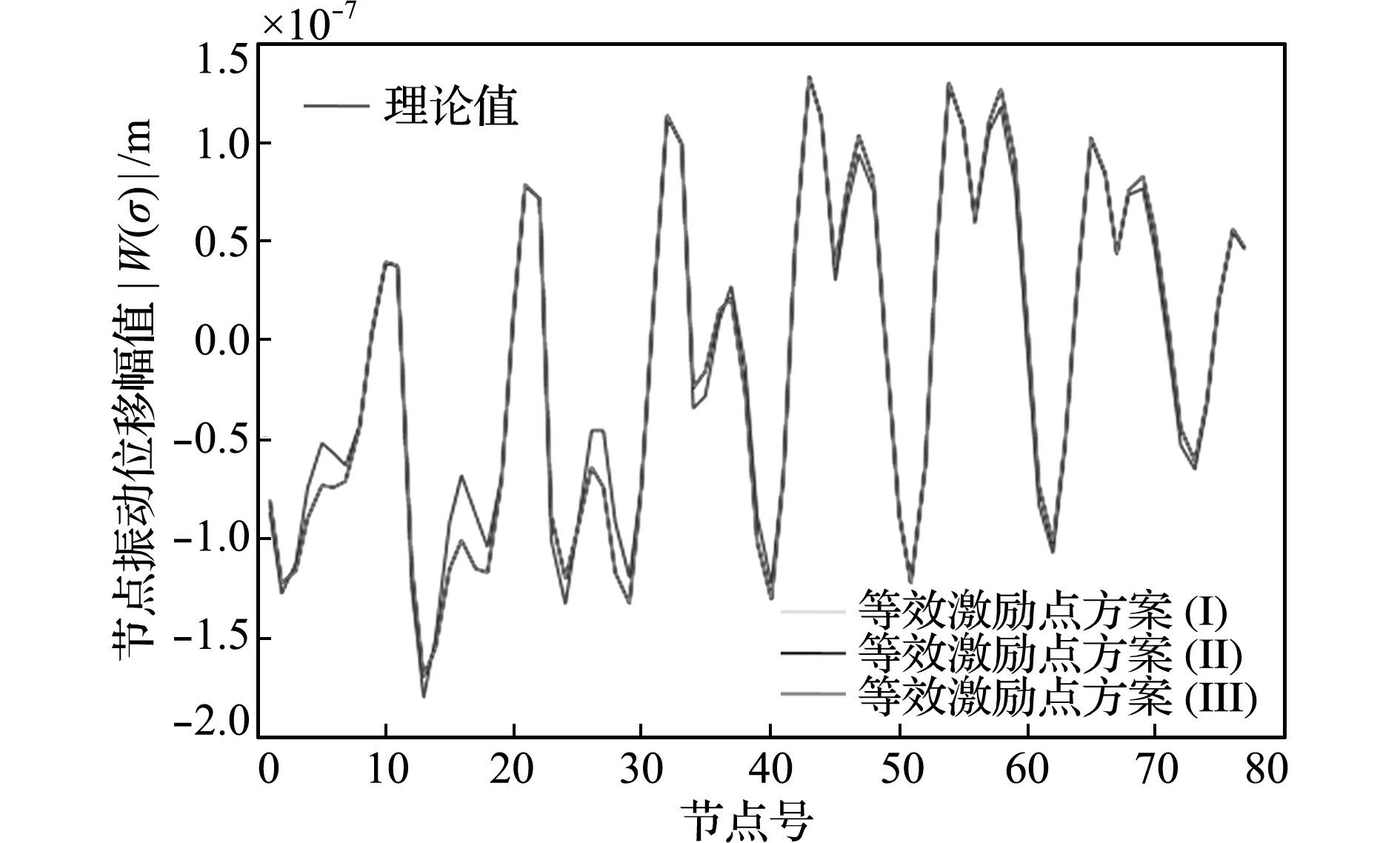
图5 等效激励与实际激励的作用效果对比
Fig.5 Comparison of the effect of the equivalent excitation and the actual excitation
可以看出,等效激励点设置的变化几乎不产生任何影响,但这一结论是有条件的。如果等效激励点数量与主要影响模态数量相等(L=N),应避免将等效激励点设定在主要影响模态的节线上,否则可能在该点上出现奇异的等效激励估计值;增加等效激励点数量(L>N)可以不受上述限制,此时等效激励的解不唯一,但利用式(9)可以确定一个具有最小均方幅值的等效激励分布形式。取L=N可以得到一个唯一的等效激励解,故而若将实际激励当作集中力看待,且所选取的等效激励点中包含了实际激励作用点(如本算例的等效激励点方案(I)),则等效激励反演能够准确地对实际激励位置和大小进行识别。已知有单一集中激励作用在某阶模态节线上而欲准确识别其大小是难以实现的情况,对此,首先应将该模态排除在主要影响模态之外(其模态影响因子理论值为0);其次,令L=N,并遵循等效激励点不设置在主要影响模态节线上的原则。
4 结合有限元法的等效激励谱估计
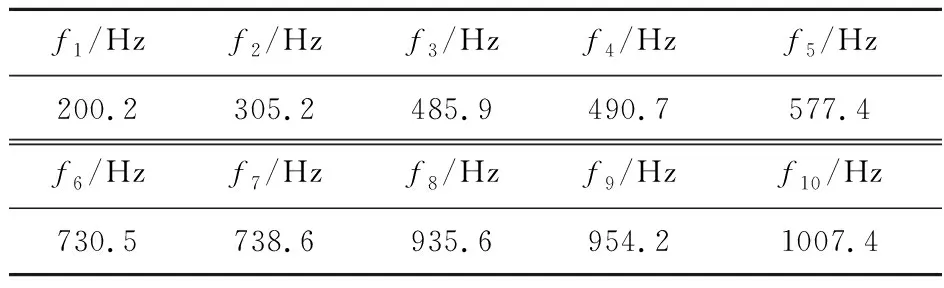
对图1矩形板,边界条件改为四边固支,则类似式(10~12)的模态表达方法不再适用,有限元法是目前通用性的方法。设四边固支矩形板仍采用如图1的网格划分单元,表1是有限元法得到的前10阶固有频率,图6是振型图形式的振型函数Ψi(σ)的有限元数值解(前4阶)。因有限元软件给出的各阶振型Ψi是正则化的,故模态质量Mi≡1。
表1 四边固支矩形薄板的前10阶固有频率
Tab.1 First 10 orders natural frequencies of rectangular thin plates with four edges clamped
f1/Hzf2/Hzf3/Hzf4/Hzf5/Hz200.2305.2485.9490.7577.4f6/Hzf7/Hzf8/Hzf9/Hzf10/Hz730.5738.6935.6954.21007.4
图6Ψ1~Ψ4的有限元数值解
Fig.6 Finite element numerical solution ofΨ1~Ψ4
为了考察宽频带等效激励谱反演的可靠性,在板上选取某节点施加具有0 Hz~700 Hz带宽的稳态单位简谐力,按响应相似原则进行等效激励谱反演,图7~图10比较了实际激励和等效激励作用下的四边固支矩形板振动位移响应。计算方法说明如下。
(1) 将分析带宽的上限(700 Hz)、下限(0 Hz)和表1的模态频率数据代入式(13),假定取α=0.2,则板的前10阶模态确定为主要影响模态。
(2) 仍如图1之方案(3)布设12个响应观测点,利用振型函数的有限元数值解导出各观测点σ处的Ψi(σ)数值,构造观测点模态矩阵Ψ。
(3) 按照实际激励作用位置未知的约定,本算例最多可以将图1全部77个内部节点都设置为等效激励点,为减少计算量,仅选取18个节点(图1 中以☆号标识的节点)作为等效激励点;利用各等效激励点σe q处的振型函数(有限元)数值解Ψi(σe q),构造等效激励点模态矩阵Ψe q。
(4) 以有限元法计算实际激励振动位移响应,将预设观测点位移响应导出,构成观测值向量W。
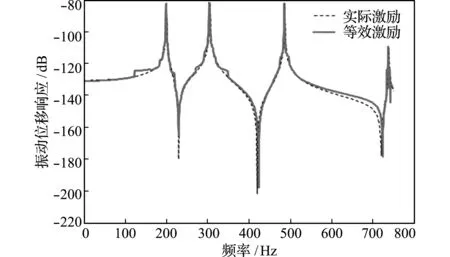
图7 25号节点的实际激励与等效激励响应谱比较
Fig.7 Comparison of response spectrum between the actual excitation and the equivalent excitation of the 25t hnode
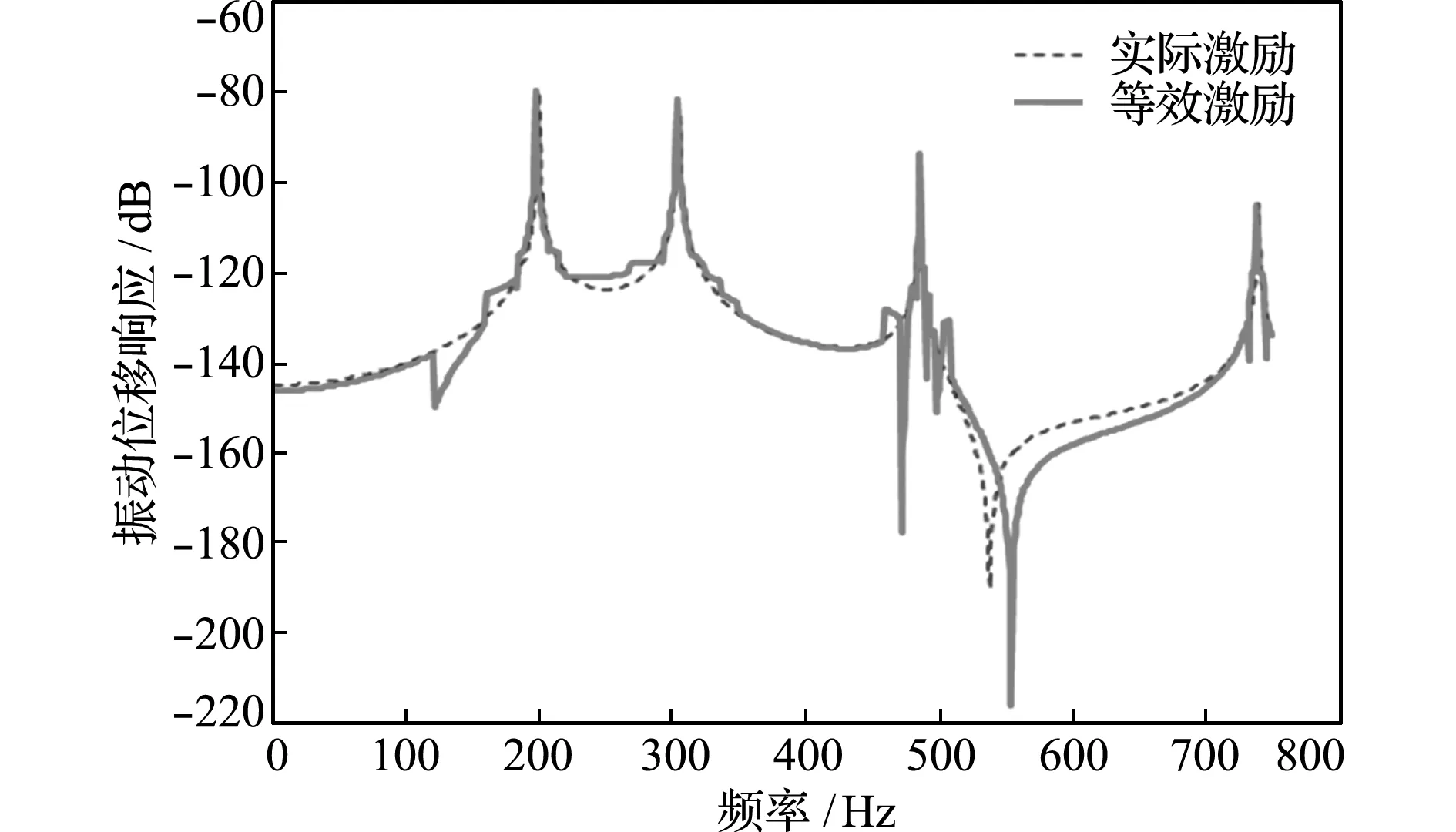
图8 52号节点的实际激励与等效激励响应谱比较
Fig.8 Comparison of response spectrum between the actual excitation and the equivalent excitation of the 52t hnode
(5) 由式(9)完成等效激励谱反演计算,以等效激励取代实际激励,重新以有限元法计算各节点的振动位移响应谱,与实际激励比较。
图7~图9分别比较了25,52和58号节点的实际激励(在38号节点上加0 Hz~700 Hz的谱激励)与等效激励的位移响应谱,图10为位移响应云图的比较。
综合图7~图10,基于主要影响模态筛选和有限观测点/等效激励点布设的等效激励谱反演效果,与实际激励的作用效果在整体上非常接近。作为一般性的理论探讨,本算例考虑了影响等效激励谱反演计算稳定性的一些不利因素,以实际激励位置未知为前提假设时,即使实际激励点(本算例38号节点)位于某些模态(本算例第4阶及其他若干阶对称型模态)节线上,也无法将这些理论影响因子为0的模态排除在主要影响模态之外;此外,本算例还将较多的等效激励点设置在主要影响模态的节线上。上述是某些频率上的等效激励响应谱发生异常波动的原因。进一步分析表明,随机地布设等效激励点并使等效激励点数量多于主要影响模态数量,可以消除等效激励谱的异常波动现象。
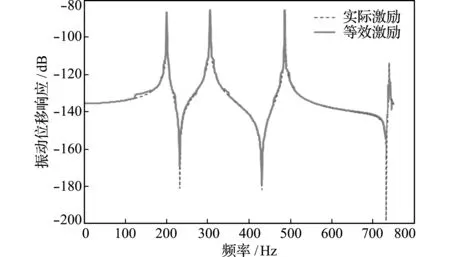
图9 58号节点的实际激励与等效激励响应谱比较
Fig.9 Comparison of response spectrum between the actual excitation and the equivalent excitation of the 58t hnode

图10 等效激励与实际激励的位移响应云图比较
Fig.10 Comparison of displacement response images between the actual excitation and the equivalent excitation
5 结 论
本文基于响应相似原则对等效激励法的可靠性和实用性进行了理论分析论证。在激励位置未知时,等效激励谱反演可用于对实际激励的作用效果进行模拟分析;若激励位置已知,则通过等效激励谱反演可实现对激励大小的识别。
等效激励估计的精度,除了振动响应测量误差之外,还受主要影响模态的筛选、响应测量点数量和布设等因素的影响。选取模态频率处于激励频率一定邻域范围内的若干阶模态作为主要影响模态,参与反演计算的模态数目过少将导致较大的模态截断误差,但数量过多亦对提高等效激励估计精度作用不大。测点数量应不少于主要影响模态数量,可以采用随机大量布设响应测量点的方法来保证模态影响因子识别结果的可信度;亦可以通过合理地分散(优化)测点布置,用较少的测点数量取得较高的识别精度。
对于等效激励点的设置,应考虑等效激励谱反演计算的稳定性,主要的指导原则是避免设置在主要影响模态的节线上。一般性地,若主要关注振动响应的一致性,则宜采取随机分散布设等效激励点并使其数量多于主要影响模态数量的方法,此时可得到具有最小均方幅值的等效激励分布形式。对实际激励位置已知而欲识别其大小的问题,应将实际激励位置包含在所设置的等效激励点中,同时使等效激励点的数量与主要影响模态数量相等;特别地,如果已知实际激励作用在某阶模态的节线上,则应额外考虑避免在该阶模态未受到显著激发的情况下将其入选到主要影响模态。
:
[1] Starkey J M,Merrill G L.On the ill-conditioned nature of indirect force -measurement techniques [J].JournalofModalAnalysis,1989,4(3):103-108.
[2] Djamaa M C,Ouelaa N,Pezerat C,et al.Reconstruction of a distributed force applied on a thin cylindrical shell by an inverse method and spatial filtering [J].JournalofSoundandVibration,2007,301(3):560-575.
[3] 毛玉明,林剑锋,刘靖华,等.动载荷反演分析技术研究综述[J].动力学与控制学报,2014,12(2):97-104.(MAO Yu-ming,LIN Jian-feng,LIU Jing-hua,et al.Recent advances of dynamic force estimation techniques[J].JournalofDynamicsandControl,2014,12(2):97-104.(in Chinese))
[4] Hu Y,Shuai Z,Li W,et al.Status quo of study on machine,s load identification technique[J].NoiseandVibrationControl,2011,4:1-5.
[5] 刘翠平.声纳部位水声场的机械自噪声传播分析[D].山东大学,2015.(LIU Cui-ping.Research on Mechanical Self-Noise of Underwater Acoustic Field in Sonar [D].Shandong University,2015.(in Chinese))
[6] Sanchez J,Benaroya H.Review of force reconstruction techniques[J].JournalofSoundandVibration,2014,333(14):2999-3018.
[7] Naets F,Cuadrado J,Desmet W.Stable force identification in structural dynamics using Kalman filtering and dummy-measurements[J].MechanicalSystemsandSignalProcessing,2015,50:235-248.
[8] Thite A N,Thompson D J.Selection of response measurement locations to improve inverse force determination[J].AppliedAcoustics,2006,67(8):797-818.
[9] Uhl T.The inverse identification problem and its technical application[J].ArchiveofAppliedMechanics,2006,77(5):325-337.
[10] 司理涛,赵 岩,张亚辉.列车荷载作用下黏弹性半空间体的随机动力响应[J].计算力学学报,2016,33(2):165-170.(SI Li-tao,ZHAO Yan,ZHANG Ya-hui.Dynamic reseponce of viscoelastic half-space subjected to train loads[J].ChineseJournalofComputationalMechanics,2016,33(2):165-170.(in Chinese))
[11] 雷 松,张文首,岳前进,等.海洋立管轴向动力响应的H∞控制[J].计算力学学报,2015,32(5):644-649.(LEI Song,ZHANG Wen-shou,YUE Qian-jin,et al.H∞control for axial dynamic response of marine risers[J].ChineseJournalofComputationalMechanics,2015,32(5):644-649.(in Chinese))
[12] Bartlett F D,Flannelly W G.Model verification of force determination for measuring vibratory loads[J].JournaloftheAmericanHelicopterSociety,1979,24(2):10-18.
[13] Giansante N,Jones R,Calapodas N J.Determination of in-flight helicopter loads[J].JournaloftheAme-ricanHelicopterSociety,1982,27(3):58-64.
[14] Okubo N,Tanabe S,Tatsuno T.Identification of forces generated by a machine under operating condition[J].ProceedingsofIMAC,1985,3:920-927.
[15] 隆昌菊.伪逆矩阵与线性方程组[J].重庆职业技术学院学报,2006,15(6):158-159.(LONG Chang-ju.Pseudoinverse matrix and linear equation[J].JournalofChongqingVocational&TechnicalInstitute,2006,15(6):158-159.(in Chinese))

