基于涡粘性模型的翼型湍流流场熵产率计算

， ， ，

(华中科技大学 能源与动力工程学院，武汉 430074)

1 引 言

翼型作为叶片的截面形状，对流体机械的工作性能起着至关重要的影响，因此翼型流场的数值计算在工程上有重要意义。传统的翼型气动性能分析侧重于在热力学第一定律的基础上进行气动力计算以及流动分离特性研究，缺乏对翼型流场中能量转换不可逆特性的研究。如果能够掌握流场中能量损失的大小及分布，就可以有针对性地改善其性能，从而提高整个流体机械的工作性能。

熵产表征系统的不可逆性及流动中能量损失的大小，基于热力学第二定律的熵分析方法，广泛应用于不可逆现象比较集中的流动与传热系统中[1-3]。Alabi等[2]将熵分析引入飞行器一体化设计中，并采用数值方法计算了B747-200整个流场的熵产。Li等[3]将熵产作为优化目标对二维翼型进行气动优化设计，却只考虑粘性耗散的熵产，未能详细分析湍流引起的熵产。Doty等[4,5]采用响应面方法对非稳态系统的熵产率进行计算。Adeyinka等[6]推导了熵的输运方程。Herwig等[7,8]采用RANS方法对熵的输运方程进行了时间平均，并将熵产分为四项。计算湍流熵产时，通常采用两种方法,文献[7]用湍动能耗散率代替脉动速度场对熵产进行求解，从而建立了湍动能耗散率与熵产的关系，但壁面处的熵产须采用经验公式单独求解；文献[8]采用涡粘性模型，通过湍流粘性系数来代替脉动速度场对熵产进行求解。

本文以NACA0012翼型为研究对象，应用RANS涡粘性模型中五种不同的湍流模型，计算不同攻角下翼型流场的熵产率，评估由粘性耗散和湍流耗散所引起的不可逆损失的大小及分布情况。翼型流场计算网格采用代数插值方法生成，通过双曲正切函数控制壁面网格间距。控制方程的离散与求解分别采用延迟修正技术(deferred correction)和强隐式法(SIP)，压力修正采用非线性的动量插值方法(MIM)。

2 控制方程与数值方法

直角笛卡尔坐标系下，稳态雷诺时均控制方程为

(1)

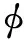
对流项和扩散项的离散采用延迟修正方法[9]。以P为节点的控制体单元第j个界面上的对流项为Cj，则

(2)

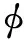
第j个界面上的扩散项Dj为

(3)

式中Sj为界面上的面积矢量，其正方向与外法向单位矢量一致。对非正交网格，将Dj分解成正交项和非正交项[10]有

(4)

式中dj为相邻两节点间的距离矢量，第一项为正交项，第二项为非正交项，将非正交项归入源项，从而避免计算单元顶点上的变量，减少了计算量。

对于得到的五对角代数方程组采用SIP方法迭代求解。

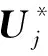
(5)

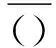
(6)

3 湍流流场熵产率计算

根据能量方程，熵的平衡方程为

(7)

由热力学第二定律，进一步推导出单位体积流体的熵产率为

(8)

式(8)表明流场的熵产率由传热产生的不可逆和流体粘性耗散的不可逆引起，其大小取决于流体的温度梯度场和速度梯度场。

当为湍流流动时，采用RANS方法对式(8)进行时均运算，有

(9)

根据Boussinesq的涡粘性假设，采用涡粘性模型EVMs(Eddy Viscosity Models)将湍流的脉动值和时均值联系起来，

(10)

式中 湍流粘性系数μt和湍流Prandtl数Prt是空间坐标函数，取决于流动状态而不是物性参数。因此，湍流的流场熵产率可以表示为

(11)

对式(11)进行体积分，可得流场总熵产率为

(12)

由上述分析可知，引入Boussinesq假设后，计算湍流流动的流场熵产率关键在于如何确定湍流粘性系数μt。当选择不同的湍流模型时，μt与湍流时均参数联系起来的关系式不同。

4 计算结果与分析

本文采用文献[15]的实验设置和实验数据，以NACA0012翼型绕流为研究目标，采用非正交同位网格下的SIMPLE算法计算雷诺数为2.88×106时，从0°攻角～16.5°攻角流场的熵产率。

翼型流场C型计算网格采用代数方法生成，在确定边界上的节点分布后，通过代数插值得到计算区域内的节点分布。为了控制翼型近壁面的节点分布，采用双曲正切关系式(13)，

(13)

为了保证壁面处第一个节点布置在对数分布律成立的范围内，让控制参数α满足给定第一个网格间距的已知条件，即

(14)

式中M为节点个数，Δs为第一层网格间距，Δq=(sM-s1)/(M-1)，s1和sM分别为起始点与终止点。

翼型的计算域和计算网格如图1所示，翼型弦长为c，入口边界距机翼后缘12.5c，为一半圆，出口边界距机翼后缘21c，为21c×25c的矩形，网格大小为240×60。

本文给定入口速度、温度和压力，出口边界条件按局部单向化处理；出口速度由内点外推得到，法向速度满足总体质量守恒条件；壁面边界为无滑移边界，当选择k-ε和RNGk-ε湍流模型时，采用壁面函数法来确定壁面上流速的有效扩散系数。

图2为NACA0012翼型在0°,10°和15°攻角下，翼型压力系数分布与实验数据的对比，可以看出,5种湍流模型的计算结果基本相同，且都和实验结果基本吻合，说明网格划分与数值方法可信。

图3为五种湍流模型在0°攻角～16.5°攻角下的流场熵产率曲线，由于不同湍流模型对于湍流粘性系数计算不同，故熵产率的计算也存在差异。可以看出，流场熵产率随着翼型攻角的增大不断增大。当攻角小于14°时，熵产率随攻角平稳增大，但随着攻角进一步增大，流场熵产率显著增大。

图4为五种湍流模型在不同攻角下的翼型壁面的阻力系数，可以看出，不同湍流模型计算得到的阻力系数变化趋势与相应湍流模型计算得到的熵产率变化趋势一致。图5给出不同湍流模型下，翼型流场熵产率与翼型阻力系数的关系，可以看出，流场熵产率与阻力系数存在线性关系。文献[3]指出，对于不可压流动，翼型阻力与流场熵产率存在如下线性关系，

(15)

进一步验证了流场熵产率计算的正确性。

传统翼型阻力的数值计算，通常采用物面压力、摩擦力积分法、远场边界面积分法和尾迹动量损失积分法[16]。式(15)从热力学第二定律能量不可逆的角度提供了一种翼型阻力的新计算方法，通过对流场熵产率的积分，得到翼型阻力。

流场熵产由粘性耗散和湍流耗散两部分组成。图6为粘性耗散的熵产率随攻角的变化曲线，可以看出，随着攻角增大，粘性耗散的熵产率会呈增大趋势，但随着攻角进一步增大至一定值时，粘性耗散的熵产率会随攻角的增加而下降。图7给出14°攻角下，不同湍流模型计算的翼型流线图。可以看出,14°攻角下，k-ε、RNGk-ε和S -A湍流模型计算流场仍为附着流，未出现分离涡结构；k-ω和SSTk-ω湍流模型下，翼型尾缘出现明显的分离涡结构。

图1 NACA0012翼型流场C型网格

Fig.1 C type mesh of NACA0012 flow field

图2 不同攻角下压力系数分布与实验值比较

Fig.2 Comparison of the pressure coefficient distribution obtained from calculation and experiment at different angle of attack

图3 不同攻角下翼型流场熵产率

Fig.3 Entropy generation rate vs.angle of attack

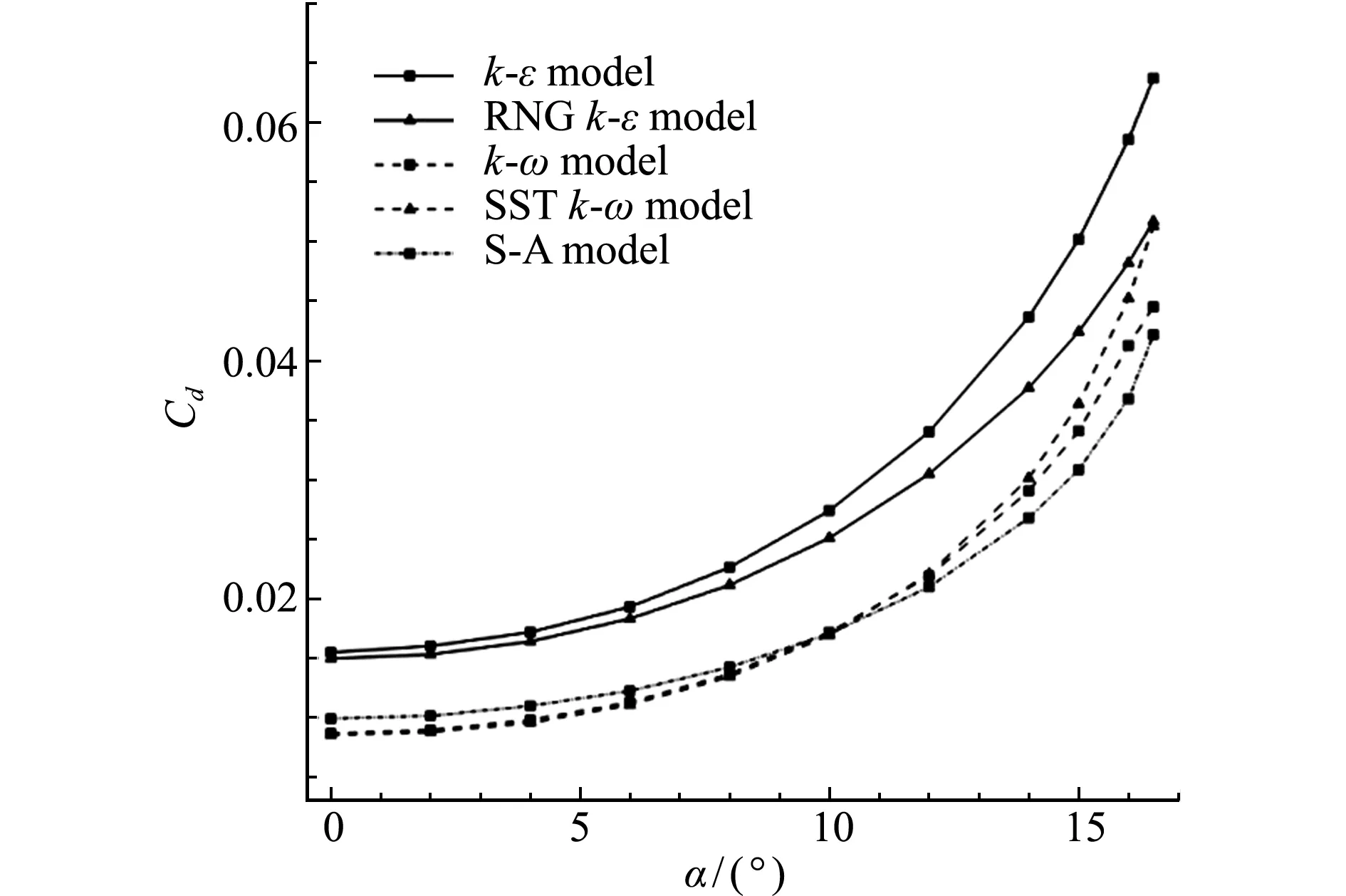
图4 不同攻角下翼型阻力系数

Fig.4 Drag coefficient vs.angle of attack

因此，当攻角增大到一定程度出现分离涡结构时，由粘性耗散引起的熵产会下降，但是由湍流耗散引起的熵产会显著上升。这是由于出现流动分离时，流场壁面附近速度梯度会变小，边界层变成紊流，使得粘性耗散的熵产降低，湍流耗散的熵产显著增加。因此，可以通过粘性耗散的熵产率曲线判定翼型产生分离涡时的攻角。

图8为10°攻角下，不同湍流模型计算的流场熵产率云图。可以看出，翼型流场的熵产主要发生在翼型前缘、近壁面边界层处以及尾流处。由式(11)可知，影响流场熵产率的主要因素是湍流粘性系数与速度梯度。翼型前缘的熵产主要由气流折转的速度梯度产生的阻力造成；近壁面边界层的熵产要远高于主流区，其本质是一种摩擦损失；湍尾流场由于尾流的高湍流度导致较大的湍流粘性系数。

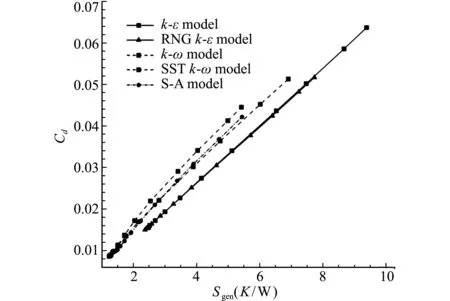
图5 翼型熵产率与阻力系数关系

Fig.5 Drag coefficient vs.entropy generation rate

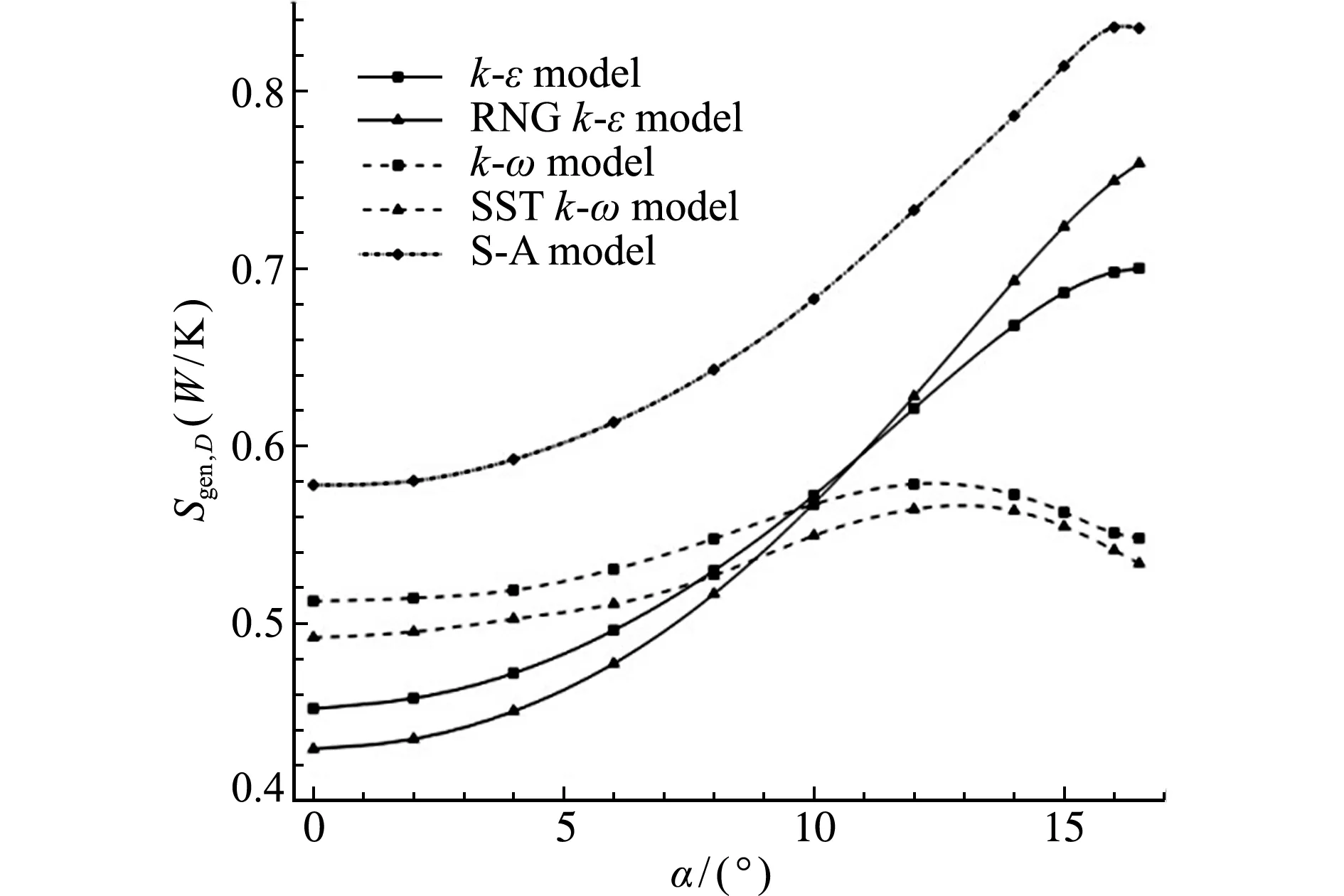
图6 不同攻角下翼型流场粘性耗散的熵产率

Fig.6 Viscous entropy generation rate vs.attack angle

图7 14°攻角下不同湍流模型流线图

Fig.7 Streamlines for attack angle 14°at different turbulence models

图8 10°攻角下不同湍流模型翼型熵产率云图

Fig.8 Contours of entropy generation rate for attack angle 10° for different turbulence models

5 结 论

本文基于非正交同位网格下的SIMPLE算法，根据涡粘性模型，对比分析了5种不同的湍流模型下翼型的流场熵产率，得到如下结论。

(1) 采用代数方法生成翼型流场的C型网格，网格生成速度快，质量便于控制；基于非正交网格下的SIMPLE算法，采用延迟修正技术和强隐式迭代方法，具有变量存储量小和计算效率高的优点。

(2) 翼型流场熵产率由粘性耗散、湍流耗散、温差传热和湍流温度脉动四部分组成，其大小取决于流体的温度梯度场和速度梯度场，其中湍流耗散是引起熵产的主要因素。翼型流场的熵产主要发生在翼型前缘区、近壁面区和翼型尾流区域。

(3) 验证了翼型流场的熵产率与翼型阻力系数为线性相关，不同的湍流模型计算流场熵产率由于湍流粘性系数计算的不同，存在差异。基于热力学第二定律的熵分析方法提供了一种翼型阻力的新计算方法。

(4) 当出现分离涡结构时，粘性耗散的熵产率下降，湍流耗散的熵产率显著上升。粘性耗散的熵产率曲线可以用来判定翼型初始产生分离涡时的攻角。

:

[1] Baker M，Riggins D，Huang J，et al.Second-law methods for the analysis & design of hypersonic vehicles[A].39t hAIAA Thermophysics Conference[C].2007.

[2] Alabi K，Ladeinde F，von Spakovsky M，et al.Asses-sing CFD modeling of entropy generation for the air frame subsystem in an integrated aircraft design/synthesis procedure[A].AIAA Aerospace Sciences Meeting and Exhibit[C].2006.

[3] Li H，Stewart J，Figliola R.Exergy based design methodology for airfoil shape optimization and wing analysis [A].25t hInternational Congress of the Aeronautical Science [C].2006.

[4] Doty J，Camberos J，Yerkes K.Approximate approach for direct calculation of unsteady entropy generation rate for engineering applications[A].50t hAIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition[C].2012.

[5] Doty J，Camberos J，Yerkes K.Comparison of entropy generation rate calculation methods for engineering applications[A].43r dAIAA Thermophysics Confe -rence[C].2012.

[6] Adeyinka O B，Naterer G F.Modeling of entropy production in turbulent flows[J].JournalofFluidsEngineering，2004，126(6):893-899.

[7] Herwig H，Kock F.Local entropy production in turbulent shear flows: A tool for evaluating heat transfer performance[J].JournalofThermalScience，2006，15(2):159-167.

[8] Moore J，Moore J G.Entropy production rates from viscous flow calculations:Part I—A turbulent boun-dary layer flow[A].ASME 1983 International Gas Turbine Conference and Exhibit[C].1983.

[9] Khosla P K，Rubin S G.A diagonally dominant second-order accurate implicit scheme [J].Computers&Fluids，1974，2(2):207-209.

[10] Mathur S R，Murthy J Y.A pressure-based method for unstructured meshes[J].NumericalHeatTransfer,1997,31(2):195-215.

[11] Stone H L.Iterative solution of implicit appro-ximations of multidimensional partial differential equations[J].SIAMJournalonNumericalAnalysis,1968,5(3):530-558.

[12] Rhie C M，Chow W L.Numerical study of the turbulent flow past an airfoil with trailing edge separation[J].AIAAJournal，1983，21(11):1525-1532.

[13] 刘 波，李忠媛，张 涛.一种基于三角形非结构化网格SIMPLE算法的程序设计[J].计算力学学报，2015，32(6):813-819.(LIU B o，LI Zhong-yuan，ZHANG Tao.A computer programming of SIMPLE algorithm based on triangle unstructured grid[J].ChineseJournalofComputationalMechanics，2015，32(6):813-819.(in Chinese))

[14] 柏 威，鄂学全.基于非结构化同位网格的SIMPLE算法[J].计算力学学报，2003，20(6):702-710.(BAI Wei，E Xue -quan.Implement of SIMPLE algorithm based on unstructured colocated meshes[J].ChineseJournalofComputationalMechanics，2003，20(6):702-710.(in Chinese))

[15] Gregory N，Reilly.Low-speed aerodynamic characte -ristics of NACA0012 aerofoil section，including the effects of upper-surface roughness simulating hoar frost[J].Cheminform，1970，23(48):6697-6700.

[16] Vinh H，van Dam C P，Yen D，et al.Drag prediction algorithms for Navier-Stokes solutions about airfoils[A].13t hAIAA Applied Aerodynamics Conference[C].1995.