基于EMD和提升小波改进阈值函数的水听器信号去噪研究

孙 强， 胡红萍，白艳萍，王 鹏

(中北大学 理学院， 太原 030051)

在探测海洋中目标时，由于光波和电磁波在海水中传播的衰减幅度较大，导致其传播距离有限，而声波却具有传播距离远和能量损失小等特点，因此水声技术[1-2]得到广泛关注和研究。考虑到海洋中声波环境复杂，对水听器接受目标信号有着很大的影响，故对水听器信号进行去噪研究很有必要。

经验模态分解(empirical mode decompositionand，EMD)是将含有噪声的目标信号分解成有限个固有模态函数，并按频率由高到低的排列顺序对其各固有模态函数(intrinsic mode function，IMF)依次展开[3]。目前许多研究人员利用EMD对一些实际问题实现了去噪，通过EMD方法将信号分解为若干IMF分量，并对其进行去噪处理后重构得到新信号。例如，文献[4]对含有噪声的激光雷达信号使用EMD方法得到一系列IMF，抛弃高频IMF并将剩余的IMF重构，达到去噪的目的；文献[5]使用EMD方法将红外遥测光谱信号分解,针对其有用信号很少且存在高频IMF和低频基线的干扰问题，通过对高频IMF和低频基线去噪提高鉴别正确率；文献[6]利用EMD方法对地震信号分解出各IMF分量，通过对各IMF分量采用小波熵阈值去噪将信号重构得到新的信号。

提升小波是小波变换的提升算法[7]。它不仅继承了小波变换的多分辨率性，而且不依赖傅里叶变换。相比传统小波变换采用Mallat算法[8]通过卷积的方式将信号中的高低频信息分离，提升小波采用原位操作，通过预测和更新两个步骤将信号中的高低频信息分离，算法更简单，且计算量小，运算速度快，因此在工程方面有着广泛的应用[9-11]。

本文提出一种EMD和提升小波改进阈值函数联和的方法对水听器信号进行去噪处理。对水听器信号经过EMD处理后得到相应固有模态函数，考虑到其噪声主要存在于高频IMF中，若只对其低频IMF进行重构虽可完成对水听器信号去噪的目的，但同时会缺失存在于高频IMF中的有用水听器信号，造成信号缺失。因此，本文采用提升小波改进阈值函数算法对每个高频IMF分量进行去噪处理，获得高频IMF中的有用信号。最后，将所有低频 IMF分量以及经过去噪处理的高频 IMF进行重构，得到新的信号。

1 EMD算法与提升小波改进阈值函数算法

1.1 EMD算法

EMD算法是根据信号的局部时间尺度产生自适应基函数，可将任何复杂信号x(t)分解为有限个IMF分量和1个残余量的和，即

(1)

式(1)中：imfi为第i个IMF分量；res为残余量。

1.2 提升小波改进阈值函数算法

提升小波算法的核心主要由3个步骤组成，分别是分裂、预测、更新。其中，在预测的步骤中通过预测算子得到提升小波的高频系数，并在更新的步骤中通过更新算子得到提升小波的低频系数。阈值方法是对小波系数进行阈值处理，将小波系数中的噪声去除，最终重构得到去噪信号。提升小波算法改进阈值函数算法的步骤如下：

步骤1 分裂：将信号s={s(k),k∈z}分裂成奇序列so={s(2k+1),k∈z}和偶序列se={s(2k),k∈z}。

步骤2 预测：由于两个序列存在相关性，故引进预测算子P(·)，通过se的预测值P(se)来预测so，将so与P(se)的差值作为高频信号d：d=so-P(se)。

步骤3 更新：信号在预测时丢失某些特征，因此需用更新算子U(·)恢复这些特征，通过d的更新值U(d)来修正se，将se与U(d)的和值作为低频信号c：c=se+U(d)。

步骤4 阈值处理：阈值方法包括硬阈值和软阈值，但是硬阈值在重构小波系数时会引起振荡的缺陷，使用软阈值时重构后的小波系数与实际值存在恒定偏差的缺陷。针对软、硬阈值的缺陷，提出了改进阈值函数为：

(2)

2 基于EMD和提升小波改进阈值函数的算法去噪

EMD算法将含噪信号分解成有限个IMF，噪声主要存在于高频IMF中，而低频IMF是由信号主导，因此通过舍去高频IMF达到信号去噪目的。但是当高频IMF中存在较多的有用信号时，若继续舍去高频IMF会造成信号失真。提升小波改进阈值函数方法在去除大部分噪声的同时会导致一小部分的有效信号被去除。本文将EMD和提升小波改进阈值函数结合，综合两者的优点，既保留低频IMF，又通过提升小波改进阈值函数对高频IMF去噪得到有用信号，改善了去噪效果。

IMF是按频率由高到低的排列顺序依次展开的，为了能将IMF划分出高频段和低频段,本文采用连续均方误差准则来确定信号高低频IMF的分界点。定义重构信号为

(3)

连续均方差准则为

(4)

高低频IMF的分界点为

(5)

式(3)～(5)中：imfk为第k个IMF分量；N为信号长度；arg min为最小函数。

本文算法的具体步骤如下：

步骤1 采用EMD分解含噪信号，得到其IMF分量。

步骤2 通过连续均方误差准则确定IMF的分界点l，并将imf1,imf2,…,imfk划分为高频IMF，imfk+1…imfn划分为低频IMF。

步骤3 对高频IMF中各分量进行提升小波改进阈值函数去噪。

步骤4 对去噪后的高频IMF以及未被提升小波改进阈值函数去噪处理的IMF进行重构，得到去噪后的信号。

3 实验

3.1 仿真实验

实验运行环境为Matlab 2014a软件平台。仿真原始信号为

x=0.5sin(2π×400t)

(6)

其中：信号频率为400 Hz；振幅为0.5；采样频率为10 kHz。实验中，加入信噪比SNR=9.615 1的噪声，形成含噪信号。图1是原始信号和含噪信号，通过本文基于EMD和提升小波改进阈值函数的算法对含噪信号进行去噪处理。

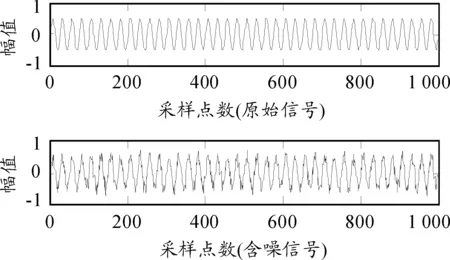
图1 原始信号和含噪信号

首先，对加噪信号使用EMD方法，含噪信号分解后的IMF分量如图2所示，包括imf1、imf2、…、imf7的7个IMF分量和1个res的残余量。

根据连续均方误差准则可知，第2层为高、低频IMF分量的分界点。因此，采用提升小波改进阈值函数方法对高频分量imf1和imf2进行去噪处理，结果如图3所示。图3(a)(c)为图2中的imf1和imf2，图3(b)(d)为imf1和imf2去噪后，从图3看出信号中大量的噪声被去除。

图2 含噪信号分解后的IMF分量

图3 imf1和imf2去噪前后对比

最后，将去噪后的imf1和imf2与未经过提升小波改进阈值函数进行去噪处理的低频IMF结合即可重构去噪后的新信号，如图4所示。仿真结果显示：含噪信号中的噪声可以被有效地去除，与仿真信号基本相同。

图4 去噪后的结果

(7)

(8)

采用定量法对去噪效果进行说明，结果见表1。从表1的结果可知：本文所提出的算法在去噪效果方面优于单一使用EMD算法与提升小波改进阈值函数的算法。

表1 去噪性能对比

3.2 实测实验

实验所用的2组数据通过水听器在汾河二库中采集。第1组数据是在环境噪声中采集1个声源信号，频率为331 Hz,如图5(a)所示。第2组数据是在环境噪声中同时采集2个声源信号，信号频率分别为331 Hz和500 Hz,如图5(b)所示。信号的采样频率都为10 kHz。采用本文的EMD和提升小波改进阈值函数算法对两组原始数据做去噪处理，结果见图6。图6是两组原始数据以及基于EMD和提升小波改进阈值函数去噪后的结果。图6(a)和(b)分别为第1组数据的信号和第2组数据的信号，图6(c)和(d)为经过EMD和提升小波改进阈值函数去噪后的第1组数据的信号和第2组数据的信号。通过对比可以发现：噪声被有效去除，且信号特征保留完整，取得了较好的去噪效果。

图5 两组信号

图6 截取信号的去噪前后对比

4 结束语

本文提出一种EMD和提升小波改进阈值函数联合的方法对水听器信号进行去噪处理。本文算法对加入噪声的仿真信号进行去噪处理，通过仿真实验证明了算法的有效性。选用信噪比和均方根误差作为评价指标对3种方法的去噪性能进行比较，说明本文基于EMD和提升小波阈值函数的算法在去噪性能方面优于单一使用EMD与单一使用提升小波阈值函数的方法。同时，将本文算法应用到水听器实测信号中进行去噪，取到了较好的去噪效果，表明该算法具有一定的实用性。

[1] 王洋东，巩庆伟，陈耀武.基于水声技术的非法作业船只远程监听系统设计[J].应用声学，2015，34(7)：66-69.

[2] 马燕芹，司纪锋.基于水声技术的黄海近海鱼类活动定点监测研究[J].渔业现代化，2016，43(4)：70-75.

[3] HUANG N E.The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London,Series A:Mathematical,Physical and EngineeringSciences,1998,454(1971):903-995.

[4] 刘增东，刘建国，陆亦怀，等.基于 EMD 的激光雷达信号去噪方法[J].光电工程，2008，35(6)：79-83.

[5] 郭腾霄，丁学全，董晓强，等.基于EMD的红外遥测光谱信号预处理新方法[J].红外与激光工程，2013，42(12)：3196-3200.

[6] 刘霞，黄阳，黄敬，等.基于经验模态分解(EMD)的小波熵阈值地震信号去噪[J].吉林大学学报(地球科学版)，2016，46(1)：262-269.

[7] SWELDENS W.The Lifting Scheme:A New Philosophy in Biorthogonal Wavelet Constructions[Z].Wavelet Applications in Signal and Image Processing,1995：68-79.

[8] MALLAT S.A wavelet tour of signal processing [M].San Diego,CA:Academic Press,1997.

[9] 王玉田，杨哲，侯培国，等.基于提升小波变换的矿物油荧光光谱去噪研究[J].光谱学与光谱分析，2016，36(7)：2144-2147.

[10] 蒋薇薇，鲁昌华，张玉钧，等.基于提升小波改进阈值的光谱信号去噪研究[J].电子测量与仪器学报,2014,28(12):363-1368.

[11] 李战明，杨守祥.基于提升小波的心电信号基线漂移的去除方法[J].中国医学装备,2014,11(3)：16-19.