除冰盐环境下预应力混凝土箱梁桥可靠度分析

彭建新，田亦昕，阳逸鸣，张建仁

(长沙理工大学 土木工程学院，湖南 长沙 410114)

在中国北方季节性冰冻地区，冬季下雪会导致道路结冰，路面湿滑。为使道路尽快通畅，常使用大量地除冰盐对立交桥进行快速除冰。常见除冰盐的主要成分为NaCl，该成分与水结合后，氯离子会轻易地渗透到混凝土桥梁结构中，使结构中的混凝土剥蚀和钢筋腐蚀，造成结构承载力降低，加速了结构的破坏。在除冰盐环境下，结构中含有大量的自由氯离子，并经受冻融循环的影响，其结构的破坏速度远超过普通环境下的破坏速度。因此，除冰盐环境所造成的环境因素变化，将直接影响结构的耐久性。

在役桥梁结构都具有抗力随时间不断变化的特点，而已有的可靠度评估法多为时不变可靠度方法(即基于设计基准期内，不考虑抗力和荷载随时间的变化来评估结构的耐久性)。结构抗力受环境变化、材料变异性及荷载作用的共同影响(即结构也有时变性)。Kiureghian[1]等人建立预应力钢绞线点腐蚀的概率模型，在考虑点腐蚀的空间变异性的前提下，进行了可靠性分析。彭建新[2]等人考虑温度、湿度及RC梁自身劣化效应影响，建立了氯离子修正模型。张德权[3]等人提出一种PHI2(I-PHI2)方法，用于求解时变可靠性区间。王茜[4]考虑可靠度的时变性，基于实桥统计参数，建立时变功能函数和抗力独立增量模型；基于载荷增量最小原则，建立失效树模型；并结合JC法和界限估计法，计算时变可靠度。卫璞[5]考虑二维坐标下的氯离子扩散浓度方法，使用响应面法，计算了结构耐久性和可靠度。易伟建[6]等人将中国和美国2种不同RC结构的设计规范进行了对比，对比了承载力设计公式和可靠指标计算结果。阳逸鸣[7]等人基于参数的空间变异性，建立了RC梁抗力时空退化模型。唐东峰[8]等人提出一种基于可靠性的连续体拓扑优化方法，将可靠度计算约束从该优化循环中解耦出来。现有试验研究多采用矩形梁或T型梁，并未考虑箱梁结构与这2种结构在承载力上的差异。学者们的研究多基于RC梁结构进行分析，较少考虑预应力对氯离子侵蚀的影响和预应力筋的腐蚀效应。因此，作者以某桥为例，拟考虑预应力对氯离子侵蚀的影响，对其在除冰盐环境下的预应力结构抗力进行计算，预测该箱梁桥腐蚀开始后100 a内的失效概率，并基于几个因素的影响进行敏感性分析。

1 模型分析

1.1 腐蚀开始时间

氯离子在桥梁结构中渗透，氯离子表面浓度到达临界浓度时，结构中的预应力筋将开始腐蚀。本研究中的梁体为预应力结构，预应力结构与钢筋结构略有不同，在受到预应力影响下，氯离子渗透速度将会产生变化。夏伟[9]引入应力影响系数f(σ)，并用关系式来表达预应力水平与氯离子扩散性能之间的关系。

Dσ=f(σ)D0。

(1)

式中：Dσ为应力σ状态下的氯离子扩散系数；D0为无应力状态下的氯离子扩散系数。

式(1)中，当混凝土处于受拉状态时，系数f(σ)=1-0.012 50σ+0.208 20σ2。

使用Fick第二定律模拟氯离子在混凝土中的扩散效应，腐蚀开始时间[10]为：

(2)

式中：C为保护层厚度；erf(·)为误差函数；C0为混凝土表面氯离子浓度；Ccr为氯离子临界浓度。

1.2 预应力筋腐蚀剩余面积

到达腐蚀开始时间Ti后，氯离子与预应力筋钝化膜发生化学反应，导致钝化膜破坏，进而加速了预应力筋的腐蚀。假设预应力筋为均匀腐蚀，那么在腐蚀电流密度icorr下，腐蚀进行ta后，一根半径为r的7丝预应力筋剩余面积Ast(t)的表达式[11]为：

Ast(t)=3πr2+4π[r-0.011 6icorr(t-

Ti)]2，Ti≤t。

(3)

1.3 结构可靠度

由规范承载能力公式和可靠度功能函数得知，随时间变化可靠度评估的极限状态方程[12]为：

Z(t)=R(t)-SG-SQ(t)。

(4)

式中：R(t)为结构自身抗力的弯矩；SG和SQ(t)分别为恒载和活载所产生的弯矩；Z(t)为结构功能函数。

由于桥梁运营过程中，混凝土强度和预应力筋面积等参数都是随着时间的变化而变化的，加之随机变量的不同分布类型，计算该桥失效概率的过程也很复杂。因此，本研究使用蒙特卡洛法进行计算。其中，对随机变量进行了1.0×107次随机抽样。具体计算流程为：

2 实例分析

2.1 实例参数

本研究以一座三跨预应力混凝土连续刚构箱梁桥为例，其主梁箱梁为单箱单室。取主跨的跨中截面参数进行抗弯计算分析，预应力筋布置及截面参数如图2所示。箱梁使用水灰比为0.33的C50混凝土和φ15.2 mm的标准预应力混凝土钢绞线。

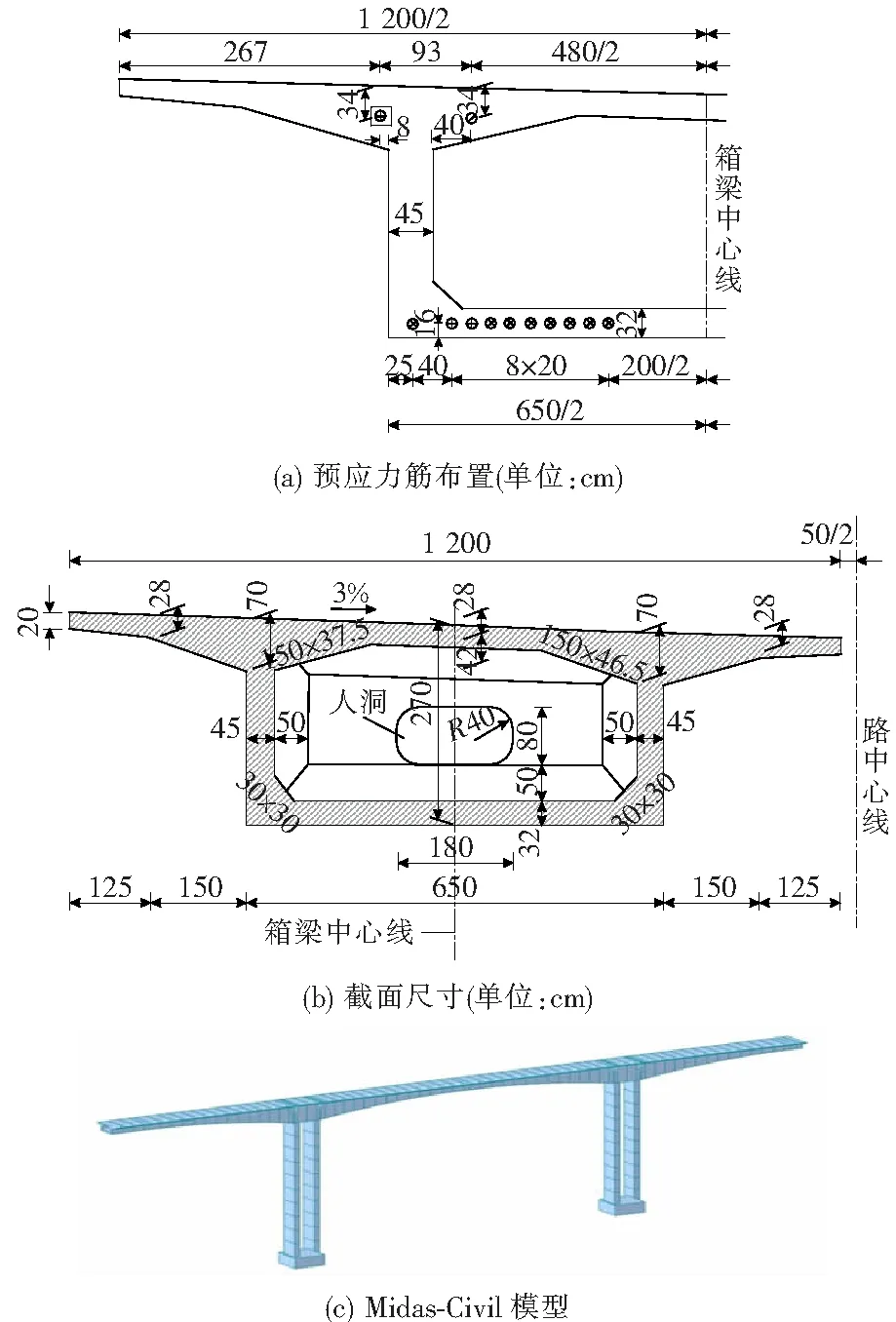
图2 箱梁跨中截面图及模型Fig.2 Cross section of the box girder and the model

该桥桥址冬季路面结冰，需使用除冰盐进行除冰。该桥主梁截面为箱型截面。根据面积和惯性矩不变的原则，将不规则的箱型梁截面等效换算为工字形梁截面，并对该桥建立Midas模型，得到恒载效应为7.56×104kN·m，车辆荷载效应为3.30×104kN·m，各统计参数见表1。

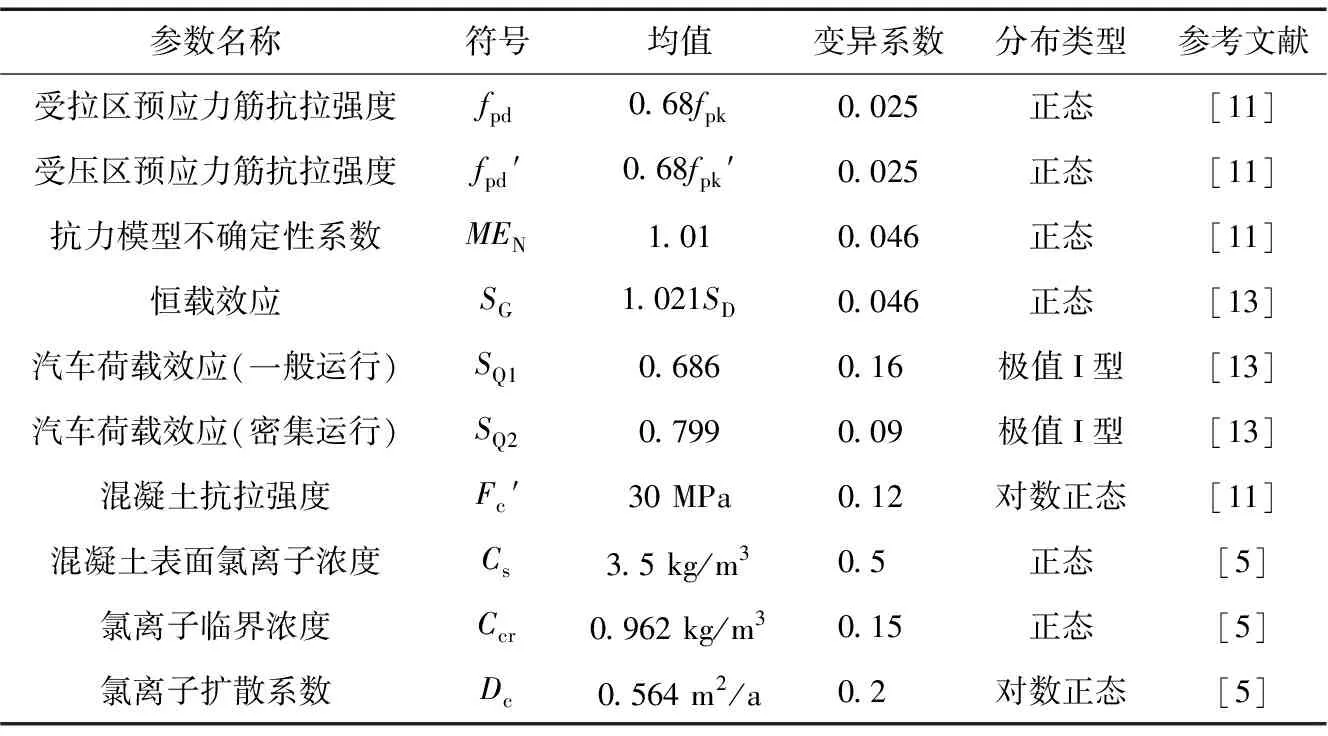
表1 参数统计表Table 1 Statistical parameters

2.2 可靠度时变模型

结合公式和实例参数，经分析和推导，该桥随时间变化的可靠度评估的极限状态方程为：

Z(t)=R(t)-SG-SQ(t)=MENfpd(t)·

Ap(t)[h0-(fpd(t)Ap(t)-fpd′(t)·

Ap′(t))÷(2fcd(t)bf′)]-SG-SQ(t)。

(5)

式中：Ap(t)和Ap′(t)分别为受压区和受压区的预应力筋在t时的剩余面积；bf′为有效宽度；h0为有效高度；fcd(t)为随时间变化的混凝土抗压强度。

2.3 结果分析

利用氯离子扩散模型、腐蚀开始时间模型、预应力筋时变腐蚀模型及可靠度时变模型，根据表1给出的该桥参数和图2所示几何尺寸参数，采用Monte-Carlo模拟方法，计算了箱梁跨中的失效概率。混凝土强度时变效应对桥梁年度失效概率的影响和对桥梁累积失效概率的影响如图3所示。从图3中可以看出，在设计寿命100 a内，同年相比，结构使用时间越长，该桥考虑混凝土强度时变效应时的失效概率大于不考虑时变效应时的失效概率，该桥考虑混凝土强度时变效应时失效概率的增长速率比不考虑时变效应时的大得多。从图3(b)中可以看出，该桥考虑混凝土强度时变效应时累积失效概率高速增长段的斜率大于不考虑时变效应时的。对数据进行线性回归后可知，该桥考虑混凝土强度时变效应时的累积失效概率约为不考虑时变效应时的1.59倍，表明混凝土强度的时变效应会影响到结构的可靠概率。

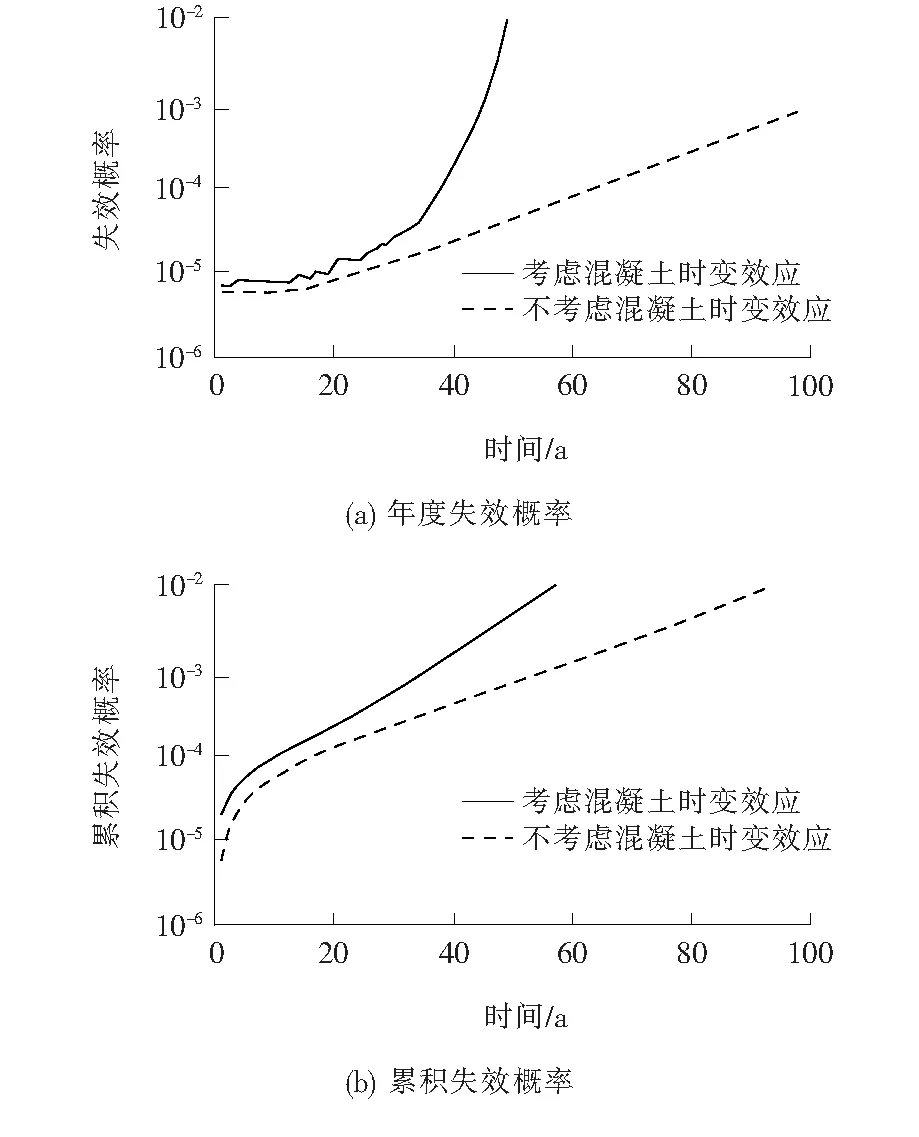
图3 混凝土强度的时变效应Fig.3 Time-varying effect of the concrete strength

考虑不同腐蚀电流密度下箱梁桥的失效概率，取文献[11]中研究所显示的腐蚀电流密度数值对结构失效概率影响较大的区间，本研究将取值间隔再加以细化，在不考虑时变效应、保护层厚度不变且其他条件相同的情况下，分别取0.1,0.2,0.3,0.4和0.5 μA/cm25个不同的腐蚀电流密度进行对比，如图4所示。从图4中可以看出，腐蚀电流密度越高，失效概率的斜率就越大，表明失效概率增加得越快。经计算可知，从腐蚀电流密度为0.2 μA/cm2开始，每一档相同间隔的腐蚀电流密度在100 a后的年度失效概率比前一档数值的年度失效概率分别高6.28,6.24,4.92和3.87倍，但这个倍数随着腐蚀电流密度的增加而逐渐减小。不同腐蚀电流密度对该桥的腐蚀失效概率的影响非常大，高腐蚀环境会大大降低结构的可靠性。表明：腐蚀电流密度的增加会导致结构失效概率的增加，但这种影响会逐渐减小。因此，腐蚀电流密度仍是评估结构耐久性必须考虑的一个因素。

图4 不同腐蚀电流密度下的失效概率Fig.4 Failure probability with different corrosion current densities

在考虑时变效应、腐蚀电流密度不变且其他条件相同的情况下，分别取55,45和35 mm 3种保护层厚度，箱梁的失效概率如图5所示。从图5中可以看出，保护层厚度为55 mm时的腐蚀概率爬升开始比保护层厚度为45 mm时的约晚5 a；保护层厚度为35 mm时的腐蚀概率爬升开始比保护层厚度为45 mm时的约早3 a。100 a后，保护层厚度为45 mm时的累积失效概率比保护层厚度为55 mm时的高75%，而比保护层厚度为35 mm时的低53%。表明：保护层厚度对于主梁的腐蚀失效有一定的影响。在合理范围内，厚的保护层厚度能在一定程度上减缓失效概率的开始，并推迟失效概率的爬升点。

图5 不同保护层厚度下的失效概率Fig.5 Failure probability with different concrete covers

3 结论

本研究建立了Midas模型，对实桥的情况进行了理论分析和数字模拟分析，得出的结论为：

1) 在计算结构失效时，应考虑混凝土强度的时变效应，不考虑该时变效应时的计算结果是偏不安全的。

2) 腐蚀电流密度对于结构失效的影响很大。高腐蚀状态下的腐蚀速度加快，结构失效概率增长较快，结构的可靠概率大大降低。为确保结构的安全，应采取措施，控制腐蚀电流密度数值的增长来源，使腐蚀电流密度降低到安全值。

3) 当混凝土保护层厚度在一定的合理范围内时，保护层厚度大的混凝土对腐蚀产生的阻碍作用也大。延缓预应力筋的腐蚀开始时间就是延长了结构的寿命。10 mm的厚度差就可以延缓失效概率，延长腐蚀开始时间平均4 a左右。在设计时，应对保护层厚度进行合理的设置。

为简化分析，本研究忽略了环境温度和湿度的变化，未考虑材料劣化、参数空间分布变化及运营期间的维护作用，需要后续做进一步的研究。

参考文献(References)：

[1] Kiureghian A D,Hong-zong L,Shyh-jiann H.Second-order reliability approximations[J].Journal of Engineering Mechanics,1987,113(8):1208-1225.

[2] 彭建新,吴婷婷,胡守旺,等.氯盐环境下预应力混凝土梁桥氯离子扩散效应及其空间概率分析[J].中国公路学报,2016,29(4):50-58.(PENG Jian-xin,WU Ting-ting,HU Shou-wang,et al.Effect of chlorides diffusion and its spatial probability analysis of prestressed concrete bridge under chloride environment[J].China Journal of Highway and Transport,2016,29(4):50-58.(in Chinese))

[3] 张德权,韩旭,姜潮,等.时变可靠性的区间PHI2分析方法[J].中国科学:物理学·力学·天文学,2015,45(5):41-53.(ZHANG De-quan,HAN Xu,JIANG Chao,et al.Interval PHI2 analysis method of time-varying reliability[J].Science China:Physics,Mechanics & Astronomy,2015,45(5):41-53.(in Chinese))

[4] 王茜.基于时变可靠度的桥梁结构安全状态评估方法[D].重庆:重庆大学,2016.(WANG Qian.Security assessment based on time-dependent reliability for bridges[D].Chongqing:Chongqing University,2016.(in Chinese))

[5] 卫璞.氯盐环境下大型混凝土桥梁构件耐久性可靠度分析[J].公路,2017,62(11):62-66.(WEI Pu.Durability reliability analysis of large concrete bridges under the chloride environment[J].Highway,2017,62(11):62-66.(in Chinese))

[6] 易伟建,何肖煌灿.中美两国混凝土结构设计规范可靠度比较[J].建筑结构,2017,47(4):1-6.(YI Wei-jian,HE Xiao-huang-can.Comparison of reliability provisions in Chinese and American codes on structural concrete design[J].Building Structure,2017,47(4):1-6.(in Chinese))

[7] 阳逸鸣,彭建新,张建仁.考虑多因素作用下的RC梁抗力时空退化模型[J].哈尔滨工业大学学报,2017,49(9):58-64.(YANG Yi-ming,PENG Jian-xin,ZHANG Jian-ren.Resistance degradation model of RC beam under the influence of many factors[J].Journal of Harbin University of Technology,2017,49(9):58-64.(in Chinese))

[8] 唐东峰,游世辉.基于可靠性的结构动态拓扑优化方法[J].湖南大学学报:自然科学版,2017,44(10):62-67.(TANG Dong-feng,YOU Shi-hui.Reliability-based structural dynamic topology optimization method[J].Journal of Hunan University:Naturnal Science,2017,44(10):62-67.(in Chinese))

[9] 夏伟.预应力混凝土中氯离子扩散试验研究及概率分析[D].长沙:长沙理工大学,2015.(XIA Wei.Experimental study and probability analysis on the chloride ion diffusion of prestressed concrete[D].Changsha:Changsha University of Science & Technology,2015.(in Chinese))

[10] 张建仁,马亚飞,王磊.模型及参数不确定下钢筋锈蚀率动态演进分析[J].中南大学学报:自然科学版,2014,45(2):542-549.(ZHANG Jian-ren,MA Ya-fei,WANG Lei.Dynamic evolution analysis of reinforcement corrosion loss under model and parameters uncertainty[J].Journal of Central South University:Naturnal Science,2014,45(2):542-549.(in Chinese))

[11] 彭建新,邵旭东,张建仁.考虑气候变化的受碳化腐蚀先张预应力混凝土梁时变可靠性评估[J].长沙理工大学学报:自然科学版,2010,7(2):34-42.(PENG Jian-xin,SHAO Xu-dong,ZHANG Jian-ren.Time-dependent reliability of prestressed concrete bridge girders subject to carbonation-induced corrosion considering climate changes[J].Changsha University of Science and Technology:Naturnal Science,2010,7(2):34-32.(in Chinese))

[12] 杨晓艳,贡金鑫,冯云芬.不同跨径桥梁车辆荷载分项系数及可靠度[J].中国公路学报,2015,28(6):59-66.(YANG Xiao-yan,GONG Jin-xin,FENG Yun-fen.Partial factors of vehicle load and reliability analysis of bridges with different spans[J].China Journal of Highway and Transport,2015,28(6):59-66.(in Chinese))

[13] 张建仁,龚文俊,刘扬.混凝土连续梁桥使用期的时变体系可靠度计算[J].长沙理工大学学报:自然科学版,2006,3(3):54-60.(ZHANG Jian-ren,GONG Wen-jun,LIU Yang.Calculation of time-dependent system reliability for continuous RC bridge during service life[J].Changsha:Changsha University of Science and Technology:Naturnal Science,2006,3(3):54-60.(in Chinese))