信号交叉口车流到达分布实证研究

郑慧敏，况爱武，段倩倩

(长沙理工大学 交通运输工程学院，湖南 长沙 410114)

交通流具有随机性和时变性等特性，尤其是由机动车、非机动车和行人构成的交叉口混合交通流更是如此。如何把握交叉口交通流的随机特征是开展交叉口优化控制的关键。Webster法、ARRB法、HCM法及冲突点法等单交叉口信号配时算法均基于稳态流理论，都未考虑交叉口进口道车辆到达率的随机性，这些方法均假定交叉口车辆到达率为某一定值，因此，所获得控制方案的控制效果与实际交通状况有较大的差异，信号控制的适应性有待加强。由于交通信号控制的各种优化指标是服从一定概率分布的，当平均值优化到一定程度时，优化指标的概率分布就显得尤为重要。

近年来，一些学者对交叉口到达车流的随机性进行了研究。如：胡明伟[1]运用K-S检验方法，检验车辆到达的统计分布规律，并且采集了部分道路的交通数据来验证。蒋阳升[2]等人对交叉口随机到达车流的时间间隔进行了拟合，发现随机车流的到达规律与其变异系数的平方存在耦合关联。也有些学者对基于可靠度的信号控制问题开展了研究，如：丁建梅[3]等人借助波动系数理论，对交通量波动的特性进行了分析，设计了信号控制参数优化算法。于泉[4]等人考虑交叉口信号控制方案与交通流时变特性之间的关系，利用可靠度指标来确定固定配时方案的启动时间，以满足交通流时变的特性。朱翼隽[5]等人假设交通的到达率服从泊松分布，将交叉口机动车流的运行过程定义为M/G/1/∞休假随机服务系统，建立了以交叉口机动车平均总等待时间为目标函数的最优随机控制模型。Lo[6]考虑交叉口入口引道车流到达的不确定性，提出了相位清空可靠性的概念。基于对数正态分布的进口道车辆到达数，建立了相位清空可靠度评价模型，并进一步构建了以相位清空可靠度为约束的交叉口信号控制优化模型。同时，还采用事件树方法，研究了交叉口存在溢流情况下的信号控制方法。但是，Lo的研究没有考虑到交叉口信号控制延误和排队长度的随机性。吕斌[7]基于Lo所提出的相位清空可靠度，在假设正态分布和负指数分布的车流达到率下，建立了信号配时优化模型，并讨论了交叉口车流到达率的随机性程度对周期时长和相位绿灯时间的影响。许多学者建立了随机条件下以交叉口机动车期望排队长度为优化目标、以相位清空可靠度为约束的孤立交叉口配时优化方法[8-9]。然而，这些基于可靠度的信号配时方法多假定交叉口到达车流服从某一种概率分布，但这些分布能否真实描述交叉口到达车流的随机性仍缺乏论证。

为保证交叉口信号控制方案的可靠度，应先确定交叉口进口道车流到达服从何种概率分布。作者以长沙市部分交叉口在不同时段、不同进口道、不同流向的车辆到达数实测数据为依据，拟运用非参数检验方法，对信号控制的交叉口进口道车流到达随机分布开展实证研究，建立具有一定普适性的概率分布模型。

1 常用分布及其参数估计

1.1 备选分布

根据交叉口车流到达实测数据直方图和学者们的相关研究，本研究选择正态分布、指数分布、对数正态分布及Wakeby分布4种概率分布模型来描述信控交叉口随机车流到达的备选分布。该4种概率分布的密度函数和待估计参数见表1。

Wakeby分布函数没有概率密度函数或者累积分布函数的解析表达式,它是由其分位函数(累积分布函数的反函数)定义的[10]。

(1)

其中，参数ξ,α,β,γ和δ应满足：β≠0，δ≠0；γ≥0；β+δ≥0；α+γ≥0；β>-1；δ<1。与传统的概率分布相比，Wakeby分布可以描述的分布形态更为广泛，只要给参数ξ,α,β,γ和δ赋予恰当的值，Wakeby分布就可以模拟出很多的偏态分布，例如：极值分布和对数正态分布等。

表1 备选分布及其参数Table 1 Alternative distributions and their parameters

1.2 备选分布参数估计

确定用某一种概率分布模型来进行随机到达车流的拟合后，应先确定该分布的参数对传统的概率分布模型。其参数估计方法比较简单，采用参数的点估计方法就能够获得参数的取值。分布的参数估计方法为：

院子里有一棵特别粗壮的老杨树。2016年深秋，我清楚地记得自己坐在杨树下面拍摄农场微电影《幸福的味道》的场景：一件破旧的针织毛衣，一条军绿色的棉布裤子，一双上世纪60年代的棉布鞋，两条长长的辫子，一种时空穿越的感觉。现在回想起来，心里还是甜甜的、暖暖的。

1) 正态分布：取大小为n的一个样本,样本观测值为x1,x2,…,xi,…,xn。参数估计的一个最直观的求法是求样本均值和样本方差。

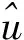
4)Wakeby分布：常用的参数估计方法并不适用于Wakeby分布，其原因是Wakeby分布没有解析形式的概率密度函数或累积分布函数，Hosking建立了Wakeby分布的L-阶矩[11]参数估计方法。该方法的基本思路是：根据样本数据计算前五阶线性矩，并令每阶矩等于由L-阶矩定义式推导得出的对应五阶矩。

L-阶矩定义为：

(2)

(3)

利用式(2)和(3)，得Wakeby分布的前五阶L-阶矩：

λ2=α[(1+β)(2+β)]-1+γ[(1-δ)(2-δ)]-1；

λ3=α(1-β)[(1+β)(2+β)(3+β)]-1+γ(1+δ)[(1-δ)(2-δ)(3-δ)]-1；

λ4=α(1-β)(2-β)[(1+β)(2+β)(3+β)·(4+β)]-1+γ(1+δ)(2+δ)[(1-δ)(2-δ)(3-δ)(4-δ)]-1；

λ5=α(1-β)(2-β)(3-β)[(1+β)(2+β)·(3+β)(4+β)(5+β)]-1+γ(1+δ)(2+δ)(3+α)[(1-δ)(2-δ)(3-δ)(4-δ)(5-δ)]-1。

根据线性矩的定义，求出Wakeby分布的前五阶线性矩后，再求取样本的前五阶线性矩。而样本的线性矩可以根据随机车流到达的样本数据求得。线性矩(L-moment)是次序统计量某种线性组合的数学期望[12]。假设：X为一实数的随机变量，其累积概率分布方程为F(X)，分位数方程为X(F)，并令X1∶n≤X2∶n≤…≤Xn∶n为n的随机样本的顺序统计量，并且该样本服从X的分布，则X的r阶线性矩为：

r=1,2,…。

(4)

式(4)中，E(Xr-k∶r)是样本容量为r时第(r-k)阶次序统计量的数学期望。则前五阶的样本线性矩计算为：

(5)

式中：br为加权概率矩(Probability Weighted Moment,简称为PWM)，br=E[X{1-F(X)}r]，r=0,1，2，…。

由车流到达的数据求得样本线性矩lr(r=1,2,…,5)后，可令其等于由公式(2)计算得到的对应L-阶矩的λr(r=1,2,…,5)，即lr=λr(r=1,2,…,5),从而得到对应的方程组。求解方程，便可得到Wakeby分布的5个参数ξ,α,β,γ和δ。

1.3 分布拟合方法

常用的分布拟合优度的检验方法有K-S、A-D和卡方(χ2)检验，本研究采用K-S检验法。对于给定的按升序排列的车流到达样本序列：x1,x2,…,xi,…,xn，假设随机车流的到达服从某一个分布,其中，F(x)为累积概率分布函数,则Fn(x)经验累积分布函数的计算公式为：

(6)

2 实例分析

2.1 数据采集

本研究以长沙市典型的2个交叉口芙蓉路与赤岭路交叉口及芙蓉路与五一大道交叉口为数据采集对象，这2个交叉口均为三相位控制的交叉口，芙蓉路与赤岭路为Y型交叉口，芙蓉路与五一大道为十字型交叉口。为了获得一般性的车流到达概率分布规律，开展了为期一周的数据观测，观测时长为全天24 h。以各交叉口各进口道1 min为时段统计车流到达数据，以1 h的数据作为一个样本，共获得了1 344组样本数据。本研究随机选择了40组不同流向、不同进口道及不同时段的数据，并将其作为研究交叉口车流到达随机性实证分析的基础数据。

2.2 实测数据分布估计

根据实测数据，分析不同流向、不同进口道及不同时段下的车流到达实测数据，共选取了40组数据。从实验数据中可以看出，不同流向、不同进口道以及不同时段的交叉口到达车流数据具有很大的波动性，要想获得一种通用的概率分布模型比较困难。以正态分布、指数分布、对数正态分布及Wakeby分布4种概率分布作为备选分布，对每一种分布用每一组样本进行参数估计,并选择K-S统计量开展假设检验，即每种分布进行40次参数估计和相应的假设检验。其结果表明：在置信水平取SL=0.05的情况下,每种分布被拒绝的次数为：正态分布拒绝9次；对数正态分布拒绝12次；指数分布拒绝37次；Wakeby分布拒绝3次。

根据实验数据可知，在这4种分布中，指数分布的拟合效果最差，其次是对数正态分布，而5参数Wakeby分布的拟合效果最好，被拒绝次数最少，只有3次。不同时段、不同流向及不同进口道车流到达的数据各不相同，但5参数Wakeby分布无论在任何情况下都能很好地拟合。进一步的分析表明：有2组车流到达数据不服从其他3种分布，只服从Wakeby分布，这2组数据的参数估计及K-S检验结果见表2。

从表2中可以看出，这2组数据只有Wakeby分布可以很好地与车流数据吻合。且只有Wakeby分布通过了K-S检验，而其他的分布均没有通过K-S检验。表明：Wakeby分布在描述信控交叉口车流到达的分布规律方面具有较大的普适性。

表2 对样本进行4种分布的参数估计和假设检验Table 2 Parameter estimation and hypothesis testing of the four distributions of samples

3 结论

本研究探讨了随机车流到达的概率分布。通过车辆到达数据，对候选的4种概率分布及5参数Wakeby分布进行了拟合，研究了参数估计方法和假设检验方法。根据样本数据，计算了前五阶线性矩。并令每阶矩等于由L-阶矩定义式推导得出的对应五阶矩，建立了等式关系求解参数。研究结果表明：Wakeby分布拟合效果最好，拒绝次数最少，只有3次。下一步将研究随机车流到达条件下信号控制相序、相位及绿信比的设计。

参考文献(References)：

[1] 胡明伟.交叉口车辆到达统计分布的实证研究[J].道路交通与安全,2009(2):10-15.(HU Ming-wei.An empirical study for vehicle arrival statistical distribution at an intersection[J].Road Traffic and Safety,2009(2):10-15.(in Chinese))

[2] 蒋阳升,韩世凡,吴婷,等.信号交叉口车辆到达规律分析[J].交通运输工程与信息学报,2015(1):1-6.(JIANG Yang-sheng,HAN Shi-fan,WU Ting,et al.Analysis of vehicle arrival law at signalized intersection[J].Journal of Transportation Engineering and Information,2015(1):1-6.(in Chinese))

[3] 丁建梅,王常虹.基于波动理论的交叉口信号控制参数优化方法[J].哈尔滨工业大学学报,2008,40(11):1717-1721.(DING Jian-mei,WANG Chang-hong.Optimization of signal control parameter at intersection with wave theory[J].Journal of Harbin Institute of Technology,2008,40(11):1717-1721.(in Chinese))

[4] 于泉,戴帅,任福田.信号交叉口固定配时控制方案可靠度研究[J].北京工业大学学报,2007,33(10):1066-1069.(YU Quan,DAI Shuai,REN Fu-tian.Control sceheme reliability research for signalized intersection[J].Journal of Beijing Polytechnic University,2007,33(10):1066-1069.(in Chinese))

[5] 朱翼隽,凌文兴.城市交通随机控制模型分析[J].运筹学杂志,1994,13(2):64-65,73.(ZHU Yi-xie,LIN Wen-xing.Analysis of urban traffic stochastic control[J].Journal of Operational Research,1994,13(2):64-65,73.(in Chinse))

[6] Lo H K.A reliability framework for traffic signal control[J].IEEE Transactions on Intelligent Transportation System,2006,7(2):250-260.

[7] 吕斌,牛惠民.信号控制交叉口可靠性建模与仿真[J].交通运输系统工程与信息,2011,11(6):45-50.(LV Bin,NIU Hui-min.Reliability modeling and simulation of signalized intersections[J].Transportation Systems Engineering and Information,2011,11(6):45-50.(in Chinese))

[8] 吕斌,牛惠民.随机条件下单点交叉口信号配时优化[J].交通运输工程学报,2010(6):116-120.(LV Bin,NIU Hui-min.Signal timing optimization at isolated intersections under random condition[J].Journal of Transportation Engineering,2010(6):116-120.(in Chinese))

[9] 吕斌,牛惠民.随机条件下单点交叉口绿灯时间计算方法研究[J].公路交通科技,2010,27(2):108-113.(LV Bin,NIU Hui-min.Calculation method of green time signal control at isolated intersection under random condition[J].Journal of Highway Communication Technology,2010,27(2):108-113.(in Chinse))

[10] HoskingJ R M,Wallis J R.Regional frequency analysis:An approach based on L-moments[M].Cambridge:Cambridge University Press,2005.

[11] Hosking J R.L-moments:Analysis and estimation of distributions using linear combination of order statistics[J].Journal of the Royal Statistical Society,1990,52(1):105-124.

[12] 陈元芳,沙志贵,陈剑池,等.具有历史洪水时P-III线性矩法的研究[J].河海大学学报:自然科学版,2001,29(4):25-29.(CHEN Yuan-fang,SHA Zhi-gui,CHEN Jian-chi,et al.Study on L-moment estimation method for P-Ⅲ distribution with historical flood[J].Journal of Hohai University:Natural Sciences,2001,29(4):25-29.(in Chinese))