多车型MAST的调度优化及关键参数分析

王正武，赵振于，何 煦

(长沙理工大学 交通运输工程学院，湖南 长沙 410114)

机动式辅助客运(mobility allowance shuttle transit，简称为MAST)是一种典型的需求响应型公交(demand responsive transit，简称为DRT)，其车辆围绕控制点确定的基准路线运行，并在可逆距离内偏离基准路线行驶，在乘客需求点上、下客(如图1所示)。MAST兼具DRT的灵活性和常规公交(固定线路、固定站点)的低成本性[1]，国外有些城市已经采用了这种公交运营模式[2]。

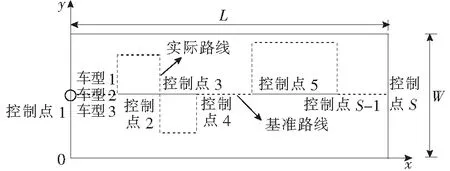
图1 多车型MAST公交运行模式Fig.1 Operation mode of the multi-class vehicle MAST system

目前，一些学者对MAST进行了研究。云亮[3]等人阐述了MAST 研究的相关进展。陈坚[4-5]等人提出了基于MAST智慧公交的系统构架。刘慧君[6]对多车辆MAST的调度问题并进行了仿真研究。林叶倩[7]等人构建了单车型MAST的混合整数规划模型。邱丰[8]等人提出了MAST的两阶段调度模型,处理静态和动态需求问题。Quadrifoglio[9-10]等人分析了双车型MAST的运行车速边界值问题，并构建了单车型MAST的插入式调度模型。Zhao[11]等人研究了单车型MAST系统的服务能力问题。Yangsheng[12]等人提出了双向多车辆MAST调度模型。现有研究主要是以单车型MAST为研究对象，但因单车型MAST的车辆容量单一，比较适应于乘客预约需求量稳定的情形；当需求量变化较大时，容易造成满载率低或滞站乘客多，因此，应根据乘客需求量选择合适的车型。在MAST调度优化中，车辆运行成本是以时间成本来计算的，无法分车型计算运行成本。而实际上，不同车型的运行成本是不同的，而且缺少可逆距离等参数对运行成本的影响分析。最大可逆距离对乘客的坐乘时间、乘客到停靠点的步行时间等有较大的影响。可逆距离的取值不同，系统的总成本就会不同。作者拟构建不同车型的运行成本函数，研究多车型MAST的调度优化模型，并确定在一定需求水平下使总成本最小的最大可逆距离。

1 多车型MAST系统的调度优化模型

1.1 模型假设

设服务区域长度为L，宽度为W，控制点(含首末站)共S(S≥2)个，车辆必须经过所有控制点，并在规定时间从控制点发车，控制点S的发车时间为TS，最大可逆距离为dback。乘客分为4类：Ⅰ类乘客上、下车地点均在基准线外的停靠点；Ⅱ类乘客上车点、下车点分别在基准线上和基准线外的停靠点；Ⅲ类乘客上车点、下车点分别在基准线外和基准线上的停靠点；Ⅳ类乘客上、下车点均在基准线上的站点。发车班次和发车时间已知，但发出车型未定。站点乘客已事先获得公交到达时间，无需在站点上等车。

1.2 出行费用函数的构建

系统中既有公交公司的运营成本，也有乘客的出行成本，二者之和即系统总成本F。设系统共有k种类型的车，则有：

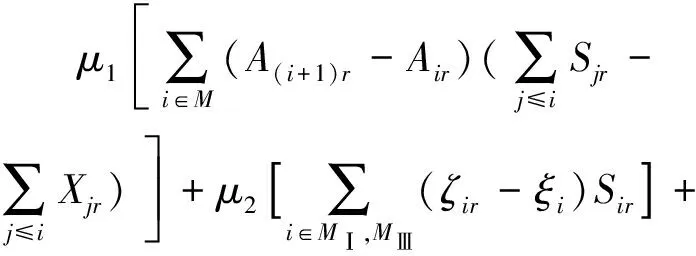
(1)

式中：μ1,μ2,μ3和μ4均为权值；NⅠ,NⅡ,NⅢ和NⅣ分别为第Ⅰ～Ⅳ类乘客的数量(NⅠ∪NⅡ∪NⅢ∪NⅣ=N)；MⅠ,MⅡ,MⅢ和MⅣ分别为第Ⅰ～Ⅳ类站点的数量(MⅠ∪MⅡ∪MⅢ∪MⅣ=M)；Air为r班次车(发出了k种类型的车) 到i站的时间；Sir，Xir分别为i停靠点上和下r班次车的人数(i停靠点对应的乘客为m类)；yi为i站点纵坐标；Yi为到i站点乘客的纵坐标；ξi为乘客到i站的时刻；ζir为乘客在i站上r班次车的时刻；dback为车辆最大逆行距离，m；τk为k种类型的车的每公里耗费，元/km；cm为m类乘客的票价，元/人；L为基准线路长度，m；α1为距离与时间的转换系数，s/m；α2为费用与时间的转换系数，s/元。

式(1)中，右边第一项为乘客乘车时间，为车辆路段行驶时间与车上乘客数之积。第二项为乘客候车时间，为乘客平均等待时间与上车乘客数之积。第三项为乘客步行时间，为平均步行距离与乘客数之积，若Yi>dback，则yi=dback；否则，yi=Yi。第四项为公交公司的净费用，也即运营成本与票价收入之差。

1.3 模型的构建

设车辆单程最大运行时间为Tmax，有r班次，从首站的发车时刻为Tr。通过计算，确定r-1(r>1)班次车发出后服务区域内剩余乘客数与r班次车发出后在Tmax内预约乘客量的和。根据该和值，初步确定r班次的发出车型(若车型最大容量小于该和值的1/n，则同时派出n辆最大容量车型的车，对n辆车按发车前、后重新排班；否则，派出车型的容量大于且最接近该和值)。然后，根据初选的r班次派出车型，优化运行路径。最后，根据优化结果，计算r班次上的最大乘客数，选定容量大于且最接近最大乘客数的车型作为r班次的派出车型。车型初选后，车辆运行路线的优化模型为：

minF

(2)

(3)

ei≤ζir≤li。

(4)

ζir≥ξi。

(5)

Tir≥ζir。

(6)

Tir>tir。

(7)

QCir≤Ck。

(8)

(9)

QCir=QCi-1,r+Sir-Xir。

(10)

|yi|≤dback。

(11)

式中：Tir和tir分别为r班次车离开和到达i站的时刻；tird为r班次车到达i站(若i为控制站)的规定时刻；QWir为r班次车到i站时站上的等待乘客数；QDir为班次r-1～班次r间隔内到i站的乘客数；QCir为r班次车到i站时的车上人数；li和ei分别为i站乘客上车时间窗的上、下界；Ck为k型车的额定载客数量，人/辆。

式(3)表示车辆到达控制站的时刻不晚于事先规定的时刻；式(4)表示乘客上车时刻满足时间窗要求；式(5)表示乘客到i站时刻应早于上车时刻；式(6)表示乘客上车时刻要早于车辆离开时刻；式(7)表示车辆离开时刻要晚于到达时刻；式(8)表示车上乘客数不能高于车辆容量；式(9)表示r班次车在i停靠点的上车人数；式(10)表示车上乘客数；式(11)表示车辆逆行距离约束。

2 求解算法设计

在调度模型中，车辆是否途经某站点是整型变量，车辆的到达时刻、出发时刻及可逆距离等是非整型变量，因此，该规划问题是混合整数规划(NP-Hard)问题。本研究基于遗传算法设计求解算法[13]，算法流程如图2所示。

在图2中，采用0和1编码途经站点，编码长度是站点总数。如：染色体为0 1 1 0 1 0 0 1 … 1，从左到右每个数表示一个站点，第一个“0”表示不经过第一个站点，第一个“1”表示经过第二个站点，以此类推)。适应度函数为系统总成本F的倒数。按文献[13]的方法进行选择、交叉及变异运算。采用最近插入法，获得初始解[13]。先由第1和第2个固定点生成一个初始路径，然后，根据车辆时间窗限制、松弛时间限制及容量限制等约束条件，不断判断控制站外的停靠点i是否具有插入路径中的可能，从而寻找到若干初始可行解。

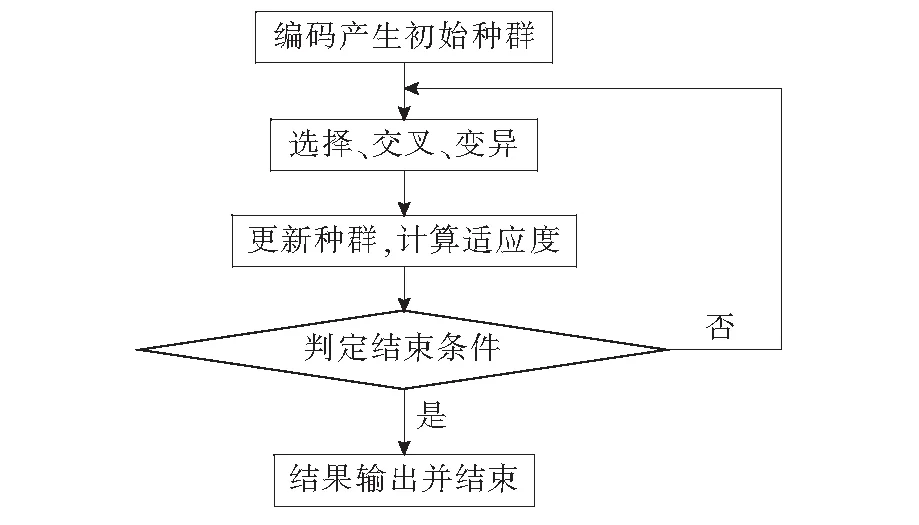
图2 遗传算法流程Fig.2 Genetic algorithm flow chart

3 算例分析

通过不同车型组合MAST与常规公交进行对比，表明多车型MAST的有效性和经济性。

3.1 乘客需求及相关参数

设发车间隔为10 min，研究时段为8∶00-9∶00，L=16 km、W=1.6 km，S=3，行驶速度v=40 km/h，票价分别为m(NI)=3元，m(NⅡ)=m(NⅢ)=2元，m(NⅣ)=1元，乘客步行速度为4.8 km/h，u1=0.2，u2=0.1，u3=0.4，u4=0.2，Tmax=40 min。对7座、12座及22座的车型，τk分别为0.6,1.2和2.0 元/km。α1=1 min/km，α2=2 min/元。低需求水平下乘客量为ρ=10人/h，中等需求水平下的乘客量为ρ=15人/h，高雪球水平下的乘客量为ρ=25人/h，最大迭代数为200，交叉和变异概率分别为0.4和0.1。车辆最大可逆距离会导致乘客类型的变化，不同可逆距离下的乘客类型比例见表1。不同需求水平下的乘客分布见表2。

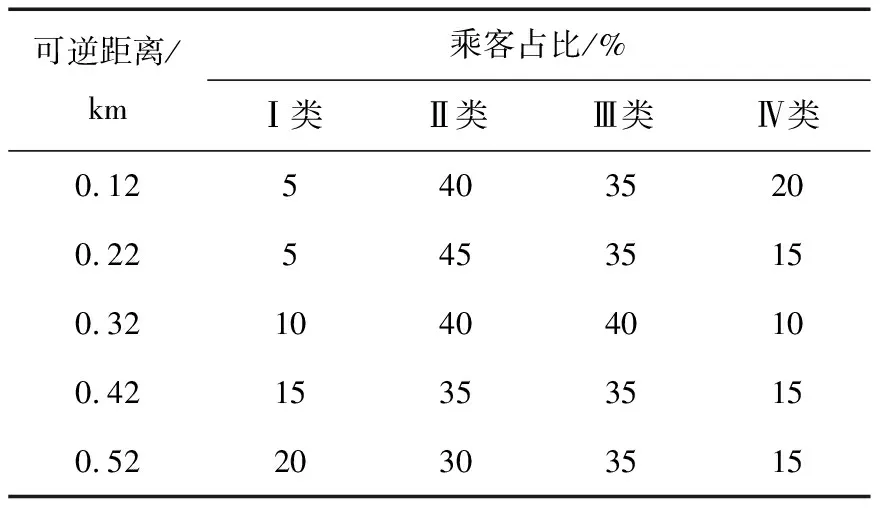
表1 不同可逆距离下的乘客类型比例Table 1 Proportion of passenger categories at different reversible distances

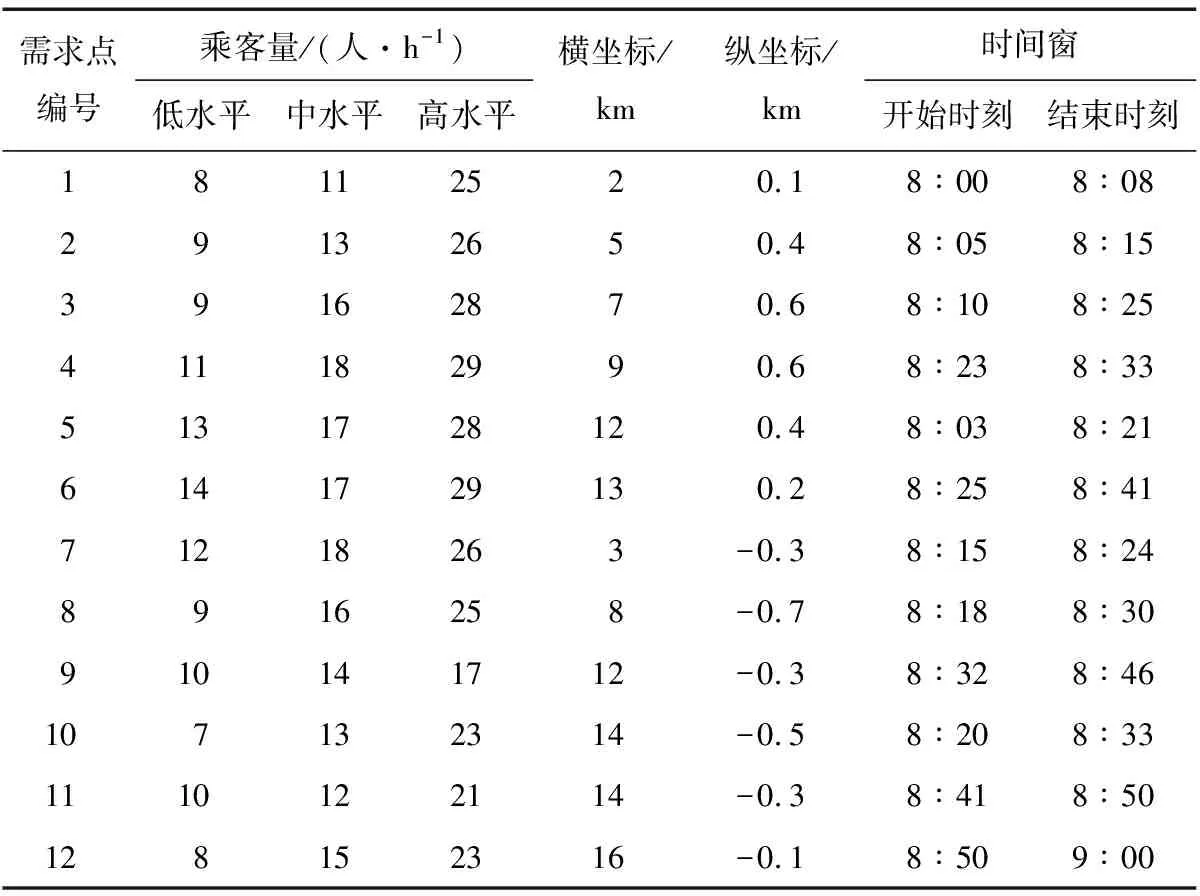
表2 不同需求水平下的乘客分布Table 2 Passenger distribution under different demand levels

3.2 实验设计

1) 实验一：不同需求水平、不同可逆距离及不同发出车型的比较实验

在低、中、高3种需求水平下，分3种情形(Q1为7座车；Q2为12座车；Q3为22座车)分析最大可逆距离分别为0.12，0.22，0.32，0.42和0.52 km时经过路径优化后系统的总成本，见表3。

从表3中可以看出：①最大可逆距离为0.32km时，各种需求水平下，各发出车型的系统成本均最小。其原因是：当可逆距离小时，乘客步行时间显著增加；当可逆距离较大时，乘客乘车时间和公交公司运行费用显著增加。②发出不同车型适应的需求水平不同。当需求量水平一定时，存在相应最适应的发车车型使系统总成本最小。如：当可逆距离0.12 km、低需求水平时，最佳车型为12座车。

表3 不同可逆距离下系统的总成本Table 3 System costs of different reversible distances

2) 实验二：不同车型组合下系统的总费用

常规公交是定点、定线的运营模式，乘客被允许在固定站点上、下车。常规公交站点间距为0.8 km，即在基准线路上可以布设21个公交站点。MAST中，最大可逆距离为0.32 km，仍考虑3种需求水平，分6种情形(Q1为7座车，Q2为12座车，Q3为22座车，Q4为7座和12座的组合型，Q5为7座、12座及22座的组合，Q6为常规公交)进行仿真，其结果见表4。

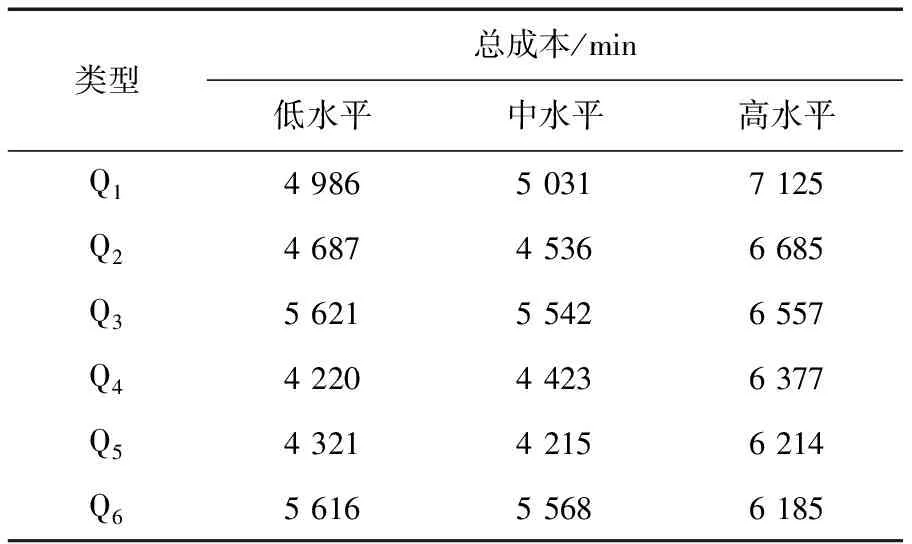
表4 MAST系统与常规公交仿真结果对比Table 4 The MAST system and conventional bus simulation results

从表4中可以看出：①需求水平较低时(ρ=10人/h)，与常规公交相比，多车型MAST系统能有效降低系统成本。其原因是：在低需求水平下，使用多车型MAST系统，虽然公交公司运营费用等增加了，但乘客的步行时间减少得很多。②需求水平高时(ρ=25人/h)，使用常规公交能降低系统总成本，因为在高需求水平下使用常规公交时，乘客步行时间等增加了，但车辆运营费用减少得很多。③在低需求量(ρ=10人/h)水平和中等需求量(ρ=15人/h)水平下，多车型MAST和单车型MAST系统均能有效降低系统总费用。其原因是单车型MAST系统和多车型MAST系统均能有效降低运营成本和乘客等待时间，提高了公交车辆的利用率。

4 结论

在分析公交公司运营成本和乘客出行费用的基础上，综合考虑乘客在车内时间、等待时间、步行时间及车辆运行时间，构建了多车型MAST的调度优化模型。由算例分析证实了该模型的经济性、有效性和适用性。为完善该模型，以后还需要研究预约型和实时申请型的混合需求MAST的调度优化问题。

参考文献(References)：

[1] Bruun E C,Marx E.Omnilink:Case study of successful flex-route-capable intelligent transportation system implementation[J].Transporation Research Record,2006,1971:91-98.

[2] Koffman D.Operational experiences with flexible transit services:A synthesis of transit practice,TCRP Report 53[R].Washington,D C:Transportation Research Board of the National Academies,2004.

[3] 云亮,蒋阳升,宋雪梅.机动式辅助客运系统(MAST)及其研究进展综述[J].交通运输工程与信息学报,2009,7(4):79-83,123.(YUN Liang,JIANG Yang-sheng,SONG Xue-mei.Introduction of mobility allowance shuttle transit system(MAST) and the summary of its research progress[J].Journal of Transportation Engineering and Information,2009,7(4):79-83,123.(in Chinese))

[4] 陈坚,李武,吴丹,等.基于MAST的智慧公交系统调度优化模型[J].重庆交通大学学报:自然科学版, 2016,35(5):140-145.(CHEN Jian,LI Wu,WU Dan,et al.Scheduling optimization model of intelligent public transport system based on MAST[J].Journal of Chongqing Jiaotong University:Natural Science,2016,35(5):140-145.(in Chinese))

[5] 陈茂林,庞明宝,张宁.基于MAST的城市郊区智慧公交调度发车计划研究[J].河北工业大学学报,2016,45(4):80-85.(CHEN Mao-lin,PANG Ming-bao,ZHANG Ning.Study on the departure plan of intelligent public transport scheduling for urban suburbs based on MAST[J].Journal of Hebei University of Technology,2016,45(4):80-85.(in Chinese))

[6] 刘慧君.多车辆机动式辅助客运系统配置仿真研究[D].成都:西南交通大学,2012.(LIU Hui-jun.Simulation study on the configuration of the multi-vehicle mobility allowance shuttle transit service system[D].Chengdou:Southwest Jiaotong University,2012.(in Chinese))

[7] 林叶倩，李文权，邱丰，等．可变线路式公交车辆调度优化模型[J].交通信息与安全，2012，30(5):14-18.(LIN Ye-qian,LI Wen-quan,QIU Feng,et al.Optimization model of variable line bus scheduling[J].Journal of Transport Information and Safety,2012,30(5):14-18,33.(in Chinese))

[8] 邱丰,李文权,沈金星.可变线路式公交的两阶段车辆调度模型[J].东南大学学报:自然科学版,2014,44(5):1078-1084.(QIU Feng,LI Wen-quan,SHEN Jin-xing.Two-stage model for flex-route transit scheduling[J].Journal of Southeast University:Natural Science Edition,2014,44(5):1078-1084.(in Chinese))

[9] Quadrifoglio L,Hall R W,Dessouky M M.Performance and design of mobility allowance shuttle transit services:Bounds on the maximum longitudinal velocity[J].Transportation Science,2006,40(3):351-363.

[10] Quadrifoglio L,Dessouky M M,Palmer K.An insertion heuristic for scheduling mobility allowance shuttle transit(MAST) services[J].Journal of Scheduling,2007,10(1):25-40.

[11] Zhao J,Dessouky M.Service capacity design problems for mobility allowance shuttle transit systems[J].Transportation Research Part B,2008,42(2):135-146．

[12] Yangsheng J,Liang Y,Huijun L,et al.Multi-vehicle system design for mobility allowance shuttle transit service[A].International Conference on Mechanic Automation and Control Engineering[C].Wuhan:[s.n.],2010:2858-2862.

[13] 任昊南.用遗传算法求解TSP问题[D].济南:山东大学,2008.(REN Hao-nan.Research on genetic algorithm for solving traveling salesman problem[D].Jinan:Shandong University,2008.(in Chinese))