抗滑桩设计的p-y曲线法及其工程应用研究

吴婷婷

(广东省冶金建筑设计研究院，广东 广州 510080)

随着中国经济的蓬勃发展，大规模的基础设施建设逐年增多，边坡工程治理问题也日益突出。因抗滑桩具有抗滑能力强、工期短及易施工等优点，在实际工程中被广泛应用[1]。

近年来，一些学者对抗滑桩设计计算问题进行了深入研究，如：年廷凯[2-3]等人基于极限分析理论和折减系数概念，建立了土坡稳定性分析的极限方程，探讨了抗滑桩技术预加固边坡的影响因素。周德培[4]等人根据抗滑桩桩间土拱效应，提出确定桩间距的方法，得到了合理桩间距的计算公式。刘钦[5-6]等人基于强度折减的有限元法或有限差分法，提供了抗滑桩加固边坡数值模拟的新方法。王聪聪[7]等人采用数值方法分析抗滑桩的加固效果，并探讨了设桩位置、桩长及桩体弹性模量等因素对边坡稳定系数、桩体内力及变形的影响。朱泳[8]等人利用有限元法，分析了抗滑桩在荷载作用下桩身内力和变形的变化规律，建立了桩身变形预测数学模型。学者们对抗滑桩加固边坡的方法和效果进行了深入的研究，但对于桩-土间相互作用的非线性研究尚少。因此，作者拟以某实际工程为例，基于p-y曲线法，推导抗滑桩挠曲微分方程及其有限差分解，分析抗滑桩的桩-土相互作用机理及其受力和变形特性，以期为类似边坡支护工程的设计提供指导和参考。

1 抗滑桩设计计算理论

1.1 计算模型及方程建立

为简化计算模型，根据抗滑桩的受力特点，可将抗滑桩分为受荷段和嵌固段2段，其中，受荷段需承受潜在滑动面以上的滑坡推力作用和桩前土体抗力的作用，如图1所示。

图1 抗滑桩的受力示意Fig.1 Loading of the anli-slide pile

p-y曲线法是一种弹塑性分析方法，能综合反映桩周土的非线性[9]。对于桩周土体不排水抗剪强度cu≤96 kPa的粘性土，可按公式确定抗滑桩的p-y曲线[9]。

(1)

y50=2.5ε50b。

(2)

式中：pu为粘性土泥面以下深度x处桩前单位长度的极限土抗力；b为桩径或宽度；x为泥面以下深度；y为地面以下x处的侧向水平变位；ε50为三轴剪切试验中主应力差达到最大主应力差一半时所对应的轴向应变。

对于cu>96 kPa的硬粘土，宜按试桩资料绘制p-y曲线。

为便于分析，根据图1所示的简化计算模型，可在抗滑桩中取一单元微段，并对其进行受力分析，如图2所示。

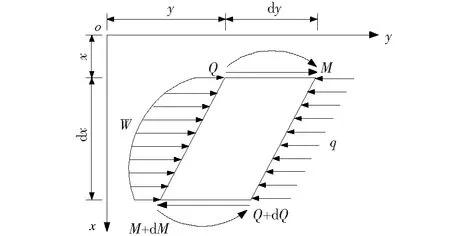
图2 受荷段微元体受力示意Fig.2 A schematic diagram of the force of a microelement in a loaded section

对图2中的微元体下端中点取矩，可得：

(3)

式中：p(y,x)为桩侧岩土体抗力；W(y,x)为滑坡推力。

略去二阶微分，并对式(3)求导，可得：

(4)

由∑y=0，可得：

(Q+dQ)+bp(y,x)dx-W(y,x)dx=Q。

(5)

(6)

令：

(7)

式中：EI为桩身抗弯刚度。

由式(4),(6)和(7)可知，受荷段桩身的微分方程为：

(8)

而嵌固段桩身的微分方程为：

(9)

假定抗滑桩桩顶与桩端的边界条件为桩顶自由和桩端嵌固[10]，其对应的微分方程分别为：

1) 桩顶自由

(10)

2) 桩端嵌固

(11)

1.2 有限差分解

利用有限差分法进行求解,其过程为：

桩身节点及其挠曲如图3所示。将基桩分成N段(每段长度h=L/N)进行离散，依据中心差分原理，在基桩上、下两端再增设2个虚拟节点。

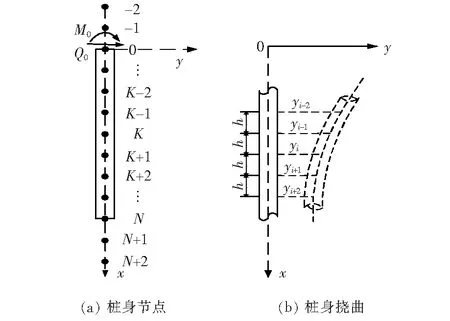
图3 桩身节点及其挠曲Fig.3 Differential points and deflection of the pile

对于受荷段的微分方程式(8)，化简后，可得基桩挠曲微分方程的差分公式：

yi-2-4yi-1+6yi-4yi+1+yi+2+

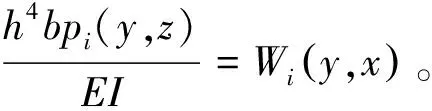
(12)

同理，将嵌固段的微分方程式(9)转化为相应的差分公式：

yi-2-4yi-1+6yi-4yi+1+yi+2+

(13)

根据桩顶边界条件式(10)，可得差分公式：

(14)

根据桩端边界条件式(11)，可得差分公式：

(15)

根据相邻桩段交界面处应满足位移、转角、弯矩及剪力相等的协调条件，其对应的差分公式为：

(16)

根据式(12)～(16)形成的方程组，求解桩身各节点的水平位移yi。利用差分公式，求得桩身的转角φi、桩身的弯矩Mi及桩身的剪力Qi。

(17)

利用MATLAB计算平台，实现迭代求解过程，计算流程如图4所示。

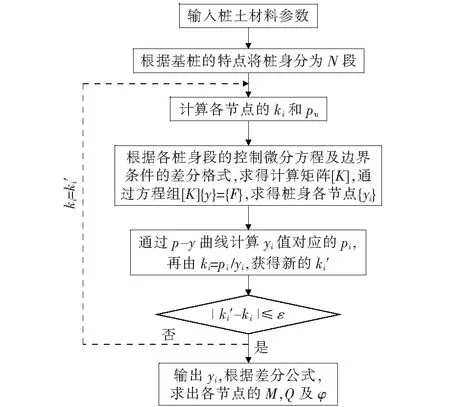
图4 p-y曲线法程序流程Fig.4 Program flow chart for p-y curve method

2 工程实例分析

2.1 工程概况

现以平(远)兴(宁)高速公路第二合同段K1595+230～K1595+350左侧路堑高边坡为例进行设计计算。该边坡长120 m，最大坡高28 m。该路段地处丘陵，地形起伏较大，地面标高约283.13～307.71 m，坡度约为19°，山坡由南向北倾斜，山体植被发育，山脊两侧为沟谷，边坡最危险断面如图5所示。

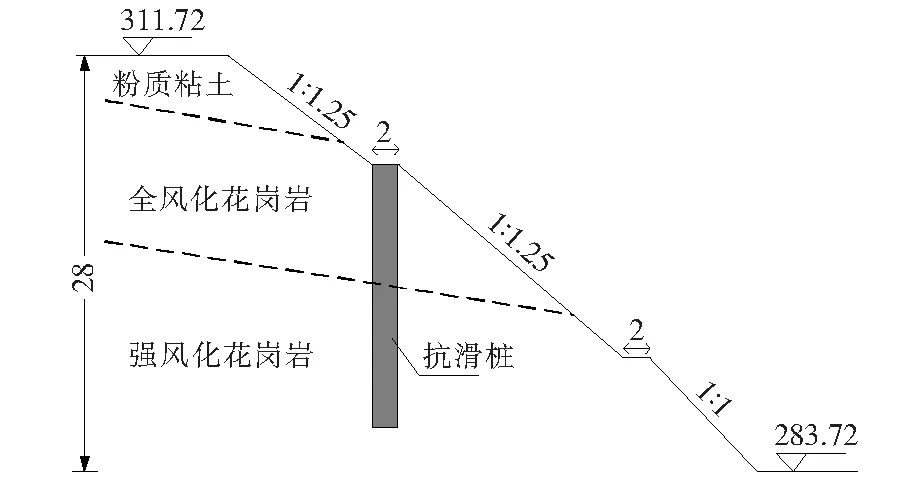
图5 最危险断面(单位：m)Fig.5 The most dangerous section map(unit:m)

2.2 计算与分析

平兴高速公路第二合同段K1595+230～K1595+350左侧路堑高边坡的计算参数为：边坡剩余下滑力为490 kN，设计桩长H=20 m，H1=12.5 m，H2=7.5 m，各土层力学参数见表1。假设剩余下滑力呈三角形分布，其峰值为70 kPa。

表1 边坡土质力学参数Table 1 Soil mechanical parameters of slope

2.2.1 桩宽的影响

桩宽是抗滑桩设计中的一个重要参数。当桩宽b为1.2,1.4,1.6,1.8和2.0 m时，桩身的水平位移和桩身的弯矩沿桩身的分布规律分别如图6，7所示。

从图6，7中可以看出，随着桩宽的增加，桩顶的最大位移和桩身的最大弯矩逐渐减小，表明增加桩宽能有效地提高边坡的稳定性。从图6，7中还可以看出，当桩宽由1.2 m按每次0.2 m依次增加时，桩顶的最大水平位移依次分别减小0.029 0,0.017 6,0.009 5和0.004 7 m，而桩身的最大弯矩依次分别减小2.565,1.675,1.056和0.700 kN·m，且减小幅度逐渐变弱。表明：增加桩宽能减小桩的变形，使抗滑桩加固边坡的效果显著。但一味增加桩宽不仅不能有效地改善抗滑桩的承载变形特性，反而造成过多的浪费。故在实际工程设计中，需要综合考虑增加桩宽的经济利益。

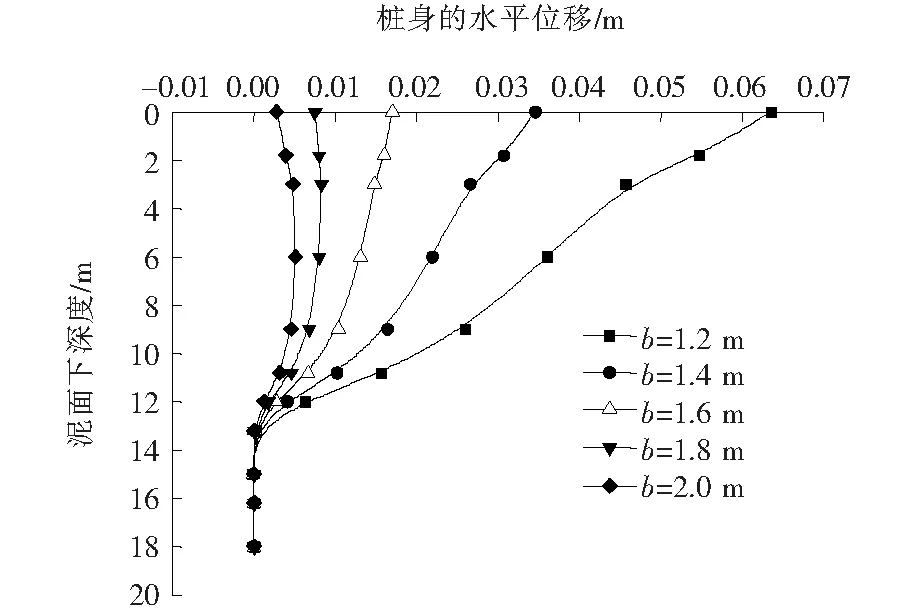
图6 不同桩宽下桩身的水平位移Fig.6 Horizontal displacement of the pile under different pile width

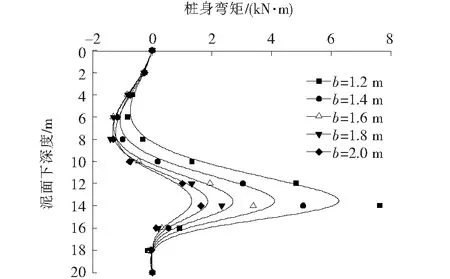
图7 不同桩宽下桩身的弯矩Fig.7 Bending moment of the pile under different pile widths

2.2.2 桩间距的影响

为分析桩间距的影响，取桩宽b=2 m，其他参数不变，只考虑改变桩间距，探讨桩间距为0.5,1.0,1.5和2.0 m时，桩身的水平位移和桩身的弯矩沿桩身的分布规律分别如图8，9所示。

从图8，9中可以看出，随着桩间距逐渐减小，抗滑桩桩顶的水平位移逐渐减小，桩身的最大弯矩的位置保持不变。表明：减小桩间距对提高边坡的稳定性具有显著效果。当桩间从2.0 m减小到1.0 m时，抗滑桩桩顶的最大水平位移减小了0.091 5 m，减幅约84%。因此，增加抗滑桩的桩宽和减小桩间距均能有效地改善边坡的稳定性，提高抗滑桩的受力和变形特性，但必须牺牲一定的经济利益。故在确定平兴高速公路第二合同段K1595+230～K1595+350左侧路堑高边坡防护加固方案时，还应该综合其他因素来确定最佳的防护加固方案。

图8 不同桩距下桩身的水平位移Fig.8 Horizontal displacement of the pile under different pile distances

图9 不同桩距下桩身的弯矩Fig.9 Bending moment of the pile with different pile distances

3 结论

以平兴高速公路第二合同段K1595+230～ K1595+350工程为例，采用p-y曲线结合有限差分法，推导了抗滑桩受力和变形设计方法，探讨了抗滑桩在不同桩宽和桩间距下的加固效果，分析了抗滑桩的桩身内力和变形特性，得出的结论为：

1) 在相同的坡体剩余下滑力作用下，随着桩宽的增加，抗滑桩桩顶的水平位移和桩身的最大弯矩均减小。增加桩宽有效地提高了加固边坡的效果。

2) 随着桩间距的减小，抗滑桩桩顶的水平位移和桩身的最大弯矩均逐渐减小，但桩身最大弯矩的位置保持不变。

3) 增加抗滑桩的桩宽和减小桩间距均能有效地改善边坡的稳定性，提高抗滑桩的受力和变形特性，但必须牺牲一定的经济利益。在实际工程设计中，还应该综合其他因素来确定最佳的防护加固方案。

参考文献(References)：

[1] 郝燕洁,杜泽丽,张建强.抗滑桩边坡加固技术的研究现状[J].市政技术,2017,35(3):145-147.(HAO Yan-jie,DU Ze-li,ZHANG Jian-qiang.Status of applied research of the slope reinforcement technology with anti-slide piles[J].Municipal Engineering Technology,2017,35(3):145-147.(in Chinese))

[2] 年廷凯,栾茂田,杨庆.抗滑桩加固土坡稳定性分析与桩基的简化设计[J].岩石力学与工程学报,2005,24(19):3427-3433.(NIAN Ting-kai,LUAN Mao-tian,YANG Qing.Stability analysis of slopes with stabilizing piles and their simplified design[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(19):3427-3433.(in Chinese))

[3] 谭捍华,赵炼恒,李亮,等.抗滑桩预加固边坡的能量分析方法[J].岩土力学,2011(S2):190-197.(TAN Han-hua,ZHAO Lian-heng,LI Liang,et al.Energy analysis method for pre-reinforcing slopes with anti-slide piles[J].Rock and Soil Mechanics,2011(S2):190-197.(in Chinese))

[4] 周德培,肖世国,夏雄.边坡工程中抗滑桩合理桩间距的探讨[J].岩土工程学报,2004,26(1):132-135.(ZHOU De-pei,XIAO Shi-guo,XIA Xiong.Discussion on rational spacing between adjacent anti-slide piles in some cutting slope projects[J].Chinese Journal of Geotechnical Engineering,2004,26(1):132-135.(in Chinese))

[5] 刘钦,李地元,刘志祥,等.水平推力作用下抗滑桩间土拱效应影响因素的数值分析[J].中南大学学报,自然科学版,2011,42(7):2071-2077.(LIU Qin,LI Di-yuan,LIU Zhi-xiang,et al.Numerical analysis of influence factors on soil arching effect between anti-sliding piles under horizontal pushing loads[J].Journal of Central South University:Science and Technology,2011,42(7):2071-2077.(in Chinese))

[6] Ashour M,Ardalan H.Analysis of pile stabilized slopes based on soil-pile interaction[J].Computers and Geotechnics,2012,39:85-97.

[7] 王聪聪,李江腾,廖峻,等.抗滑桩加固边坡稳定性分析及其优化[J].中南大学学报:自然科学版, 2015，46(1):231-237.(WANG Cong-cong,LI Jiang-teng,LIAO Jun,et al.Stability analysis of slope reinforced with piles and optimization[J].Journal of Central South University:Science and Technology,2015,46(1):231-237.(in Chinese))

[8] 朱泳,朱鸿鹄,张巍,等.抗滑桩加固边坡稳定性影响因素的参数分析[J].工程地质学报,2017,25(3):833-840.(ZHU Yong,ZHU Hong-hu,ZHANG Wei,et al.Parametric analysis on factors influencing stability of slopes reinforced by anti-slide piles[J].Journal of Engineering Geology,2017,25(3):833-840.(in Chinese))

[9] American Petroleum Institute.(RP2A-WSD) Recommended practice for planning, designing, and constructing fixed offshore platforms-working stress design[S].Washington D C: American Petroleum Institute,2000.

[10] 宁夏元,尹平保,谢上飞.高陡横坡段桥梁桩基设计计算方法及工程应用[J].公路工程,2012,37(4):56-61.(NING Xia-yuan,YIN Ping-bao,XIE Shang-fei.The design and calculation method and its applications of bridge piles in steep cross slope[J].Highway Engineering,2012,37(4):56-61.(in Chinese))