基于改进自适应粒子滤波的无线传感网船舶追踪

梅骁峻， 吴华锋， 陈彦臻， 蒋恩青

(上海海事大学商船学院， 上海 201306)

0 引 言

船舶追踪是保障船舶安全航行的一个关键环节。最早的对进出港船舶的追踪方法是：从船舶交通管理系统(vessel traffic service，VTS)获得船舶监控视频，手动标定视频每一帧图像中的监控船舶，得到船舶轨迹。然而，当本船与他船的船型相差不大且成像区域有重叠时，采用这种方法追踪船舶较容易出现失误[1]。为提高船舶追踪效率和精度，一种采用闭路电视(closed-circuit television，CCTV)的船舶追踪法被用于船舶监控。它综合考虑了船舶的静态信息和动态信息，使船舶追踪精度有所提高[2]，但在恶劣天气下船舶追踪效果不理想。对于在公海航行的船舶的追踪方法有雷达追踪和卫星追踪，然而由于受到海杂波的干扰，采用这些方法进行船舶追踪的效果不理想[3]。因此，本文提出一种新的基于无线传感网(wireless sensor network, WSN)的船舶追踪方法。

WSN是一种自组织的网络，包含有许多能感知到信息的传感节点，利用通信功能使消息在网络中传递。由于这些传感节点成本低、功耗低，WSN被广泛应用于许多领域，包括环境监测、目标追踪等[4-6]。由于海上的环境复杂，且节点会随海浪的运动而运动，海上节点的布置以及船舶追踪受到了巨大的挑战。LUO等[7]对海上WSN节点的布置问题做了详细的阐述，并利用三层检测系统对船舶进行检测追踪，但未考虑节点的计算量以及高噪声海杂波的干扰等问题。

粒子滤波(particle filter, PF)通过一系列带权重的粒子估计后验概率分布，并以此为样本对节点的状态进行估计和计算，能够很好地适应非线性以及非高斯的系统，故常被应用于高噪声环境中的目标追踪[8]。许多学者对PF物标追踪做了研究：赵洪宇等[9]提出了自适应PF (adaptive PF, APF)算法，利用KL散度(Kullback-Leibler divergence, KLD)重采样的方法对PF进行优化从而实现了自适应船舶追踪；钟雄庆等[10]提出基于卫星电子信息的PF目标追踪方法，采用二阶自回归的状态转移模型确定候选量测的关联区域，随后利用卫星电子信息选取粒子权值并进行状态更新及位置估计；李倩[11]提出基于PF的移动目标追踪方法，利用积分图算法、亮度补偿等对PF的计算量进行了优化；崔威威等[12]利用PF在信噪比较低时对物标有良好追踪效果的特性，提出改进的VTS目标检测跟踪算法，提升了追踪精度。由上述研究可知，PF算法对高噪声环境中的物标追踪有较好的效果。然而，由于受到海浪遮蔽效应的干扰，将PF算法用于海洋WSN，追踪船舶的效果并不好；同时，为防止粒子退化，对大量粒子进行重采样会使节点计算量增大，节点寿命缩短。

为减少海洋WSN节点计算量，提高船舶追踪精度，本文提出基于改进APF(impoved APF, I-APF)的WSN船舶追踪方法：首先对APF进行改进，提出最优的边界阈值；随后根据船舶在海上航行中的运动特点建立状态方程和观测方程；最后通过仿真来验证本文提出算法的性能。

1 PF算法

PF算法是基于序列重要性采样的蒙特卡洛方法，其系统模型为

式中：f()表示状态转移函数；x(t-1)和x(t)分别表示上一时刻和此刻的状态；u(t-1)表示均值为零、方差为Q的高斯状态转移噪声；h()表示测量函数；v(t)表示均值为零、方差为R的高斯测量噪声；z(t)表示在t时刻的观测值。

PF算法的思想就是通过先验概率分布来估计后验概率分布：

(3)

其中

η=P(z(t)|z(1:(t-1)))=

(4)

式中：z(1:t)和z(1:(t-1))分别表示从1到t和到t-1时刻的观测值。式(3)中的先验信息可表示为

P(x(t)|z(1:(t-1)))=

(5)

然而，实际情况下后验概率分布难以获得，通常可利用一个已知的且易于采样的重要性概率密度Π(x(t)|z(1:t))来获得样本值(当样本足够大时Π(x(t)|z(1:t))≈P(x(t)|z(1:t)))，随后通过规范化权值和重采样对位置进行估计：

(6)

在得到后验概率分布后，利用它对节点的位置进行估计：

(7)

为避免粒子的退化，重采样在PF中必不可少。序列重要性重采样(sequential importance resampling, SIR)方法是目前用得最多的一种重采样方法，它通过保留权值大的粒子、剔除权值较小的粒子来解决粒子退化问题。在给定时刻L的情况下，传统PF算法流程见图1。

图1 传统PF算法流程

2 I-APF算法

由于传统PF算法在每次迭代时都要对固定数量的粒子进行重要性采样，存在计算量大、实时性差的问题，近年来许多学者利用KLD重采样的方法来实现自适应选择粒子，并提出APF算法。

用KLD表示两个概率分布P1与P2之间的距离：

(8)

两个概率分布之间的距离为非负数；当两个概率分布一致时，距离为零。

当P1与P2之间的距离小于ε时，采样粒子数量为

(9)

式中：ε表示提前设定的阈值；K表示不同的子空间；1-∂表示APF中每次粒子迭代的概率。

通过χ2分布量化，保证P1与P2之间的逼近误差最小：

P(χK-12≤χK-1,1-∂2)≈1-∂

(10)

为简化计算，引入Wilson-Hilferty转换[13]，式(9)可表示为

(11)

式中：Z1-∂表示标准正态分布的1-∂分位数的上界。

(12)

式中：Nmax表示最大粒子数量；C表示返回大于或等于指定表达式的最小整数。

APF算法往往是基于预设好的阈值ε来实现其自适应特性的，但在实际情况下预设好的阈值ε并非最优阈值。因此，本文就要找寻最优的边界阈值εopt对APF算法进行改进。

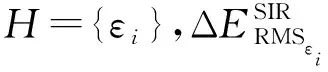
在获取最优的阈值εopt后，假设已知t-1时刻的粒子集合，则I-APF算法可描述为算法2：

由于微电子机械系统-惯性测量(MEMS-IMU)成本低、体积小，能够监测到船舶经过某区域时所引起的海浪加速度的变化，并利用瞬时傅里叶变化对海浪信号进行处理，从而实现对船舶的探测[7,15]，故本文假设在节点预置MEMS-IMU，采用三层检测系统[7]探测监测区域的船舶。预先向监测区域部署3种节点：普通节点、簇头节点和汇聚节点。普通节点用于探测船舶经过监控区域时所引起的海浪加速度的变化，并将相应的数据发送给簇头节点；为减少由风或动物或其他外界因素带来的噪声干扰，簇头节点对收到的数据进行处理和融合，随后将其发送给汇聚节点；汇聚节点对数据进行进一步处理后发送给用户或卫星。当船舶经过监测区域时，普通节点感知到海浪加速度的变化，便开始自适应采样粒子，并将相应数据发送给簇头节点；簇头节点利用其数据处理功能对数据进行时间、空间上的校正，降低外界因素的噪声并发送给汇聚节点做进一步的数据处理。当船舶位置超出节点所能感知的范围时，节点采样停止。

3 仿真实验

为验证本文提出算法的有效性，用MATLAB R2014a进行仿真。仿真参数设置如下：定位追踪区域为1 000 m×1 000 m；海浪遮蔽效应引起的测距噪声误差为7.98 dB；路径损耗指数为2.4[16]。

节点的状态方程可描述为

(13)

式中：x(t)和x(t-1)分别表示锚节点此刻和上一时刻的状态；T表示锚节点的采样周期；u(t-1)表示状态转移噪声。

由于需要广泛布置节点，为减少通信开销，选取信号强度指示器(receive signal strength indicator, RSSI)的值作为节点间的测量模型[16]。

(14)

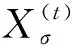
设定ε的取值范围为(0，1)，Δε=0.05，最大粒子数Nmax=1 000。

将本文提出的I-APF算法与APF算法和PF算法在计算时间、均方根误差、追踪效果方面进行比较。

均方根误差可表示为

(15)

图2表明I-APF算法在采样周期内的计算时间优于APF和PF算法；在迭代开始时由于粒子状态不稳定，故3种算法计算时间突然增长。由于粒子初始化时间也包含在仿真时间中，故最初的迭代时间内无计算时间。表1为3种算法的平均计算时间。由表1可知，虽然3种算法的计算时间均较短，但I-APF算法明显优于其他两种算法。

图2 3种算法在采样周期内的计算时间表1 采样周期内的平均计算时间

算法I-APFAPFPF时间/s0.0150.0320.072

图3表明，采用I-APF算法时船舶追踪的均方根误差优于采用APF和PF算法时船舶追踪的均方根误差。均方根误差随着时间的推移而增大是因为累积误差的增多。粒子首先要进行初始化，故3种算法在开始一段时间后才进行误差计算。为验证I-APF算法船舶追踪的效果，采用三层检测系统[7]探测监测区域的船舶，在仿真区域部署6个节点：节点2、节点3和节点5为普通节点；节点1和节点4为簇头节点；节点6为汇聚节点。图4表明本文提出的I-APF算法比APF算法在船舶追踪方面效果好，但随着船舶航行距离的增加，追踪效果较初始时略有降低。这是因为船舶逐渐远离传感节点部署区域，能监测到船舶的传感节点减少，从而导致船舶追踪精度下降。

图3 采用3种算法的船舶追踪均方根误差图4 船舶的真实航迹及采用 I-APF算法、APF算法时得到的航迹

4 结 论

针对无线传感网(WSN)节点对船舶追踪精度不高、计算量大的问题，提出改进自适应粒子滤波的WSN船舶追踪算法(I-APF算法)。该算法对传统KL散度(KLD)算法进行改进，通过迭代找出最优的阈值εopt，随后在重采样阶段实现自适应粒子采样。相较于APF算法，I-APF算法在粒子采样的数量上实现了自适应，可避免因采样粒子过多而导致的计算时间长的问题，同时还能保证追踪的精确度。该算法可用于海上军事对抗时追踪本船的航迹，从而判断本船是否偏航，同时还能获取他船的运动轨迹从而达到监测的目的。

参考文献：

[1] 云霄, 肖刚. 基于Camshift的多特征自适应融合船舶跟踪算法[J]. 光电工程, 2011, 38(5): 52-58. DOI: 10.3969/j.issn.1003-501X.2011.05.010.

[2] 赵航, 李栋, 袁剑华, 等. 一种VTS系统中CCTV对船舶跟踪监控方法[J]. 雷达与对抗, 2016， 36(2): 12-14.

[3] DANIEL L, HRISTOV S, LYU Xiaoyong,etal. Design and validation of a passive radar concept for ship detection using communication satellite signals[J]. IEEE Transactions on Aerospace & Electronic Systems, 2017, 53(6): 3115-3134. DOI: 10.1109/TAES.2017.2728978.

[4] YANG Y, WANG C. Wireless rechargeable sensor networks[M/OL]. Heidelberg: Springer International Publishing, 2015[2018-04-02]. https://link.springer.com/content/pdf/10.1007/978-3-319-17656-7.pdf. DOI: 10.1007/978-3-319-17656-7_1.

[5] OBAIDAT M S, MISRA S. Principles of wireless sensor networks[M]. Cambridge: Cambridge University Press, 2014: 1-433.

[6] PRABHU S R B, GAJENDRAN E, BALAKUMAR N. Contemporary challenges in environmental monitoring application of wireless sensors[J]. International Journal of Universal Science and Engineering, 2016(2): 30-40.

[7] LUO Hanjiang, WU Kaishun, GUO Zhongwen,etal. Ship detection with wireless sensor networks[J]. IEEE Transactions on Parallel & Distributed Systems, 2011, 23(7): 1336-1343. DOI: 10.1109/TPDS.2011.274.

[8] GU Dongbing. Distributed particle filter for target tracking[C]//IEEE International Conference on Robotics and Automation. IEEE, 2007: 3856-3861.

[9] 赵洪宇, 王伟, 蔡爱华. 基于自适应粒子滤波算法的对海跟踪研究[J]. 现代雷达, 2014, 36(3): 49-52.

[10] 钟雄庆, 邹焕新, 雷琳, 等. 粒子滤波的卫星电子信息舰船目标跟踪算法[J]. 信号处理, 2015, 31(10): 1318-1323. DOI:10.3969/j.issn.1003-0530.2015.10.015.

[11] 李倩. 移动视频目标跟踪中的智能过滤算法研究[J]. 舰船科学技术, 2017，39(1A): 112-114.

[12] 崔威威, 黄孝鹏, 姚远, 等. 基于粒子滤波改进的VTS微弱目标检测前跟踪算法[J]. 火力与指挥控制, 2016, 41(5): 141-144. DOI:10.3969/j.issn.1002-0640.2016.05.034.

[13] TERRELL G R. The Wilson-Hilferty transformation is locally saddlepoint[J]. Biometrika, 2003, 90(2): 445-453.

[14] LI T, SUN S, SATTAR T P. Adapting sample size in particle filters through KLD-resampling[J]. Electronics Letters, 2013, 49(12): 740-742. DOI: 10.1049/el.2013.0233.

[15] ARIFIN A S, FIRDAUS T S. Ship location detection using wireless sensor networks with cooperative nodes[C]//2017 9th International Conference on Ubiquitous and Future Networks(ICUFN). IEEE, 2017: 433-437.

[16] WU Huafeng, YANG Lei, LIU Ling,etal. Real-time localization algorithm for maritime search and rescue wireless sensor network[J]. International Journal of Distributed Sensor Networks, 2013, 9(3): 188-192. DOI: 10.1155/2013/791981.