基于Matlab/Simulink的欠驱动机械臂仿真实验

赵海滨, 刘 冲, 陆志国, 颜世玉, 于清文

(东北大学 机械工程与自动化学院, 辽宁 沈阳 110819)

Pendubot是在垂直平面上运动的欠驱动两自由度机械臂[1-3]。Pendubot系统的驱动电机安装在第一个关节,为主动臂；第二个关节可以自由运动,为欠驱动臂。Pendubot系统具有非线性和强耦合等特性,并作为欠驱动的基准系统,用于验证复杂的非线性控制算法。Pendubot系统的控制方式包括摆起控制和平衡控制,在摆起控制和平衡控制之间通过切换控制器进行切换。

Pendubot系统的摆起控制方法主要有部分反馈线性化方法[4]、能量控制方法[5-6]、混杂控制方法[7]、模糊控制方法[8]和滑膜控制方法[9-10]等；平衡控制方法常用线性二次型调节器(LQR)。本文在分析Pendubot系统的动力学方程的基础上,利用Matlab/Simulink建立Pendubot系统模型,然后采用部分反馈线性化方法进行摆起控制,采用LQR进行平衡控制,并设计了切换控制器。通过对典型的Pendubot系统进行仿真验证,向学生完整地展示系统的控制过程,加深学生对Pendubot系统的理解,增强学生的实际动手能力和学习兴趣,增强欠驱动系统的理论和实验教学效果。

1 Pendubot系统

欠驱动Pendubot系统由2个关节组成。第一个关节是主动臂,第二个关节是欠驱动臂,如图1所示。q1和q2分别表示主动臂和欠驱动臂角度,m1和m2分别为主动臂和欠驱动臂的质量,l1和l2分别为主动臂和欠驱动臂长度,lc1和lc2分别表示主动臂和欠驱动臂相对于质心的距离,I1和I2分别表示主动臂和欠驱动臂的转动惯量。

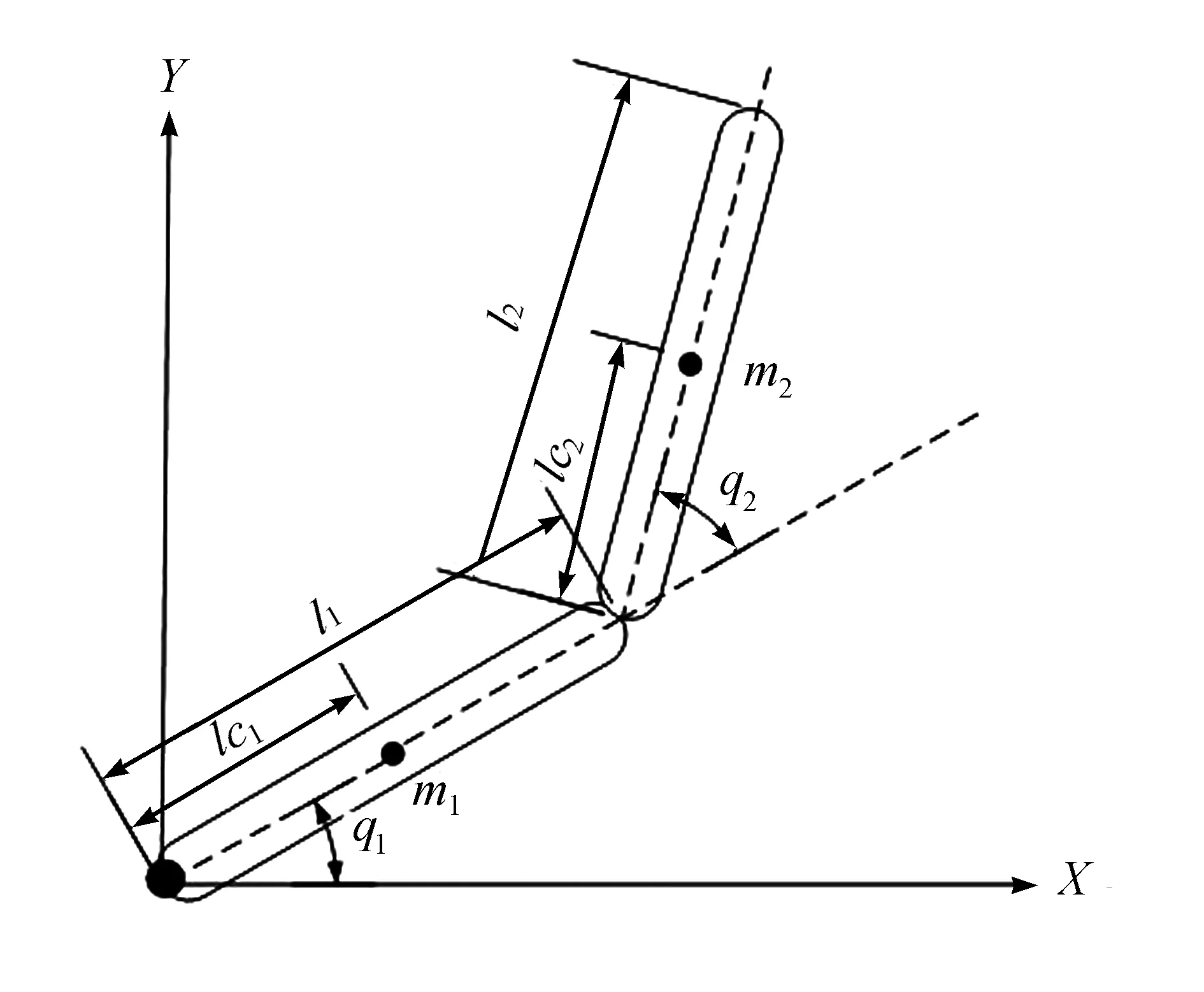
图1 欠驱动两杆机械臂Pendubot

通过拉格朗日方程建立Pendubot系统的动力学方程[11-12]为

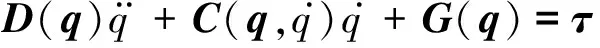
(1)

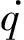
τ=[τ1，0],为驱动力矩向量；

为惯性矩阵；

为重力势能矩阵；

为科里奥利和离心力的结合矩阵。

(2)

Pendubot系统动力学方程中的参数用下面5个新参数表示

(3)

将这些参数代入Pendubot系统的动力学方程,可以得到:

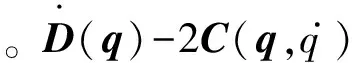
2 控制器

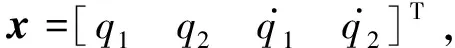
2.1 摆起控制器

在Pendubot系统的摆起控制中,部分反馈线性化方法具有算法简单、驱动力矩小和摆起时间短等优点,因此本文采用部分反馈线性化方法。将Pendubot系统的动力学方程写成如下形式：

(4)

(5)

(6)

式中

采用部分反馈线性化进行摆起控制[4],主动臂的驱动力矩为

(7)

(8)

其中,参数kp>0和kd>0。当Pendubot位于竖直向上的静止状态时,主动臂的角度为π/2,角速度为0,控制器的输入u也为0。

2.2 平衡控制器

在竖直向上的位置x2进行线性化,可以得到

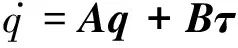
(9)

其中参数A和B为常数矩阵。平衡控制器采用LQR,LQR具有很好的鲁棒性,目的是在一定的性能指标下,使系统的控制效果最佳,即利用最少的控制量来达到最小的状态误差。LQR控制器的力矩为

τ1=-Kx2

(10)

参数K为最优状态反馈矩阵,在Matlab软件中采用函数lgr()进行计算。函数lgr()的调用格式为K=lqr(A,B,Q,R),其中参数Q为单位矩阵,R为1。通过计算,Pendubot系统在位置x2处的参数K为

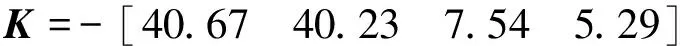
2.3 切换控制器

在摆起控制和平衡控制之间需要进行控制器的切换。主动臂和欠驱动臂位于竖直向上的位置附近时,进行控制器的切换,控制器切换的条件为

(11)

其中参数t1为1.4,参数t2为0.8。式(11)表示主动臂和欠驱动臂位于竖直向上位置x2附近,进行控制器的切换。当由摆起控制器切换为平衡控制器时,一直采用平衡控制器,不能再切换为摆起控制器。

3 仿真实验平台

Matlab功能强大、使用简单方便,并且对问题的描述和求解符合人们的思维习惯和数学表达习惯,已经广泛应用于动态系统仿真[13]。Simulink是Matlab软件最重要的组件之一,能够进行动态系统建模、仿真和综合分析。根据Pendubot系统的动力学方程,采用Matlab/Simulink软件建立仿真模型和控制器,控制器包括摆起控制器、平衡控制器和切换控制器。采用Simulink中用户自定义功能模块库中的Matlab Function模块、积分模块和使能子系统来建立整个系统,如图2所示。

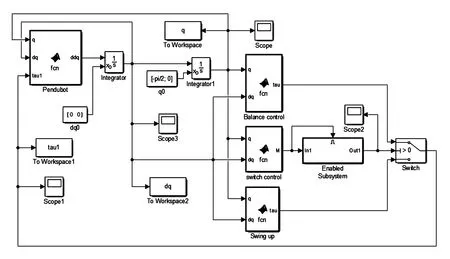
图2 Pendubot系统仿真实验平台

functionddq = fcn(q, dq, tau1)

q1=q(1); q2=q(2); dq1=dq(1); dq2=dq(2);

t1=0.0308; t2=0.0106; t3=0.0095;

t4=0.2086; t5=0.0630;g=9.81;

q2=mod(q2, 2*pi);

d11=t1+t2+2*t3*cos(q2);

d12=t2+t3*cos(q2);

d21=d12; d22=t2;

c11=-t3*sin(q2)*dq2;

c12=-t3*sin(q2)*(dq2+dq1);

c21=t3*sin(q2)*dq1;

g1=t4*g*cos(q1)+t5*g*cos(q1+q2);

g2=t5*g*cos(q1+q2);

D=[d11, d12; d21, d22];

C=[c11, c12; c21, 0];

G=[g1; g2];

ddq=D([tau1; 0]-C*[dq1; dq2]-G); //公式(2)

根据式(7)和式(8)可以建立摆起控制器。在式(8)中,参数kp为44.2,参数kd为8.8。在图2中,摆起控制器模块Swing up内的代码如下：

function tau = fcn(q, dq)

q1=q(1); q2=q(2); dq1=dq(1); dq2=dq(2);

t1=0.0308; t2=0.0106; t3=0.0095;

t4=0.2086; t5=0.0630; g=9.81;

q2=mod(q2, 2*pi);

d11=t1+t2+2*t3*cos(q2);

d12=t2+t3*cos(q2);

d21=d12; d22=t2;

c11=-t3*sin(q2)*dq2;

c12=-t3*sin(q2)*(dq2+dq1);

c21=t3*sin(q2)*dq1;

g1=t4*g*cos(q1)+t5*g*cos(q1+q2);

g2=t5*g*cos(q1+q2);

fd11=d11-d12*d21/d22;

fc11=c11-d12*c21/d22;

fc12=c12;

fg1=g1-d12*g2/d22;

kp=44.2; kd=8.8;

v1=kp*(pi/2-q1)-kd*dq1; //公式(8)

tau=fd11*v1+fc11*dq1+fc12*dq2+fg1;//式(7)

Pendubot系统的平衡控制器采用LQR,即式(10)。在图2中,平衡控制器模块Balance control内的代码如下：

function tau = fcn(q,dq)

q1=q(1); q2=q(2); dq1=dq(1); dq2=dq(2);

K=-[40.67, 40.23, 7.54, 5.29];

tau=-K*[q1-pi/2; q2; dq1; dq2]; //公式(10)

切换控制器采用式(11),在图2中,切换控制器模块switch control内的代码如下：

function M = fcn(q,dq)

q1=q(1); q2=q(2); dq1=dq(1); dq2=dq(2);

t=abs(q1-pi/2)+abs(q2)+0.1*abs(dq1)+...

0.1*abs(dq2);

if q1>1.4 //公式(11)

if t<0.8 M=1; else M=0; end

elseM=0;end

通过切换控制器,将摆起控制器切换为平衡控制器,并通过使能子系统,使系统一直采用平衡控制器。在图2中,主动臂的驱动力矩通过Switch模块具体进行切换操作,积分模块的初始值设置为初始状态x1,通过To Workspace模块将运行结果保存在工作空间中。

4 仿真设计实例

在仿真过程中,采用变步长的ode45算法,最大步长为0.001 s,仿真时间为3 s。采用的Pendubot系统参数[6]为θ1=0.0308vs2,θ2=0.0106vs2,θ3=0.0095vs2,θ4=0.2086vs2/m,θ5=0.0630vs2/m。

Pendubot系统仿真实验的运行结果如图3和图4所示。在图3中,主动臂的最大力矩为3.09 N·m,最小力矩为-0.90 N·m,主动臂的力矩最终趋近于0。在图4中,Pendubot系统的初始状态为竖直向下的位置,q1=-π/2和q2=0。最终稳定的状态为竖直向上的位置,q1和q2分别趋近于π/2和0。

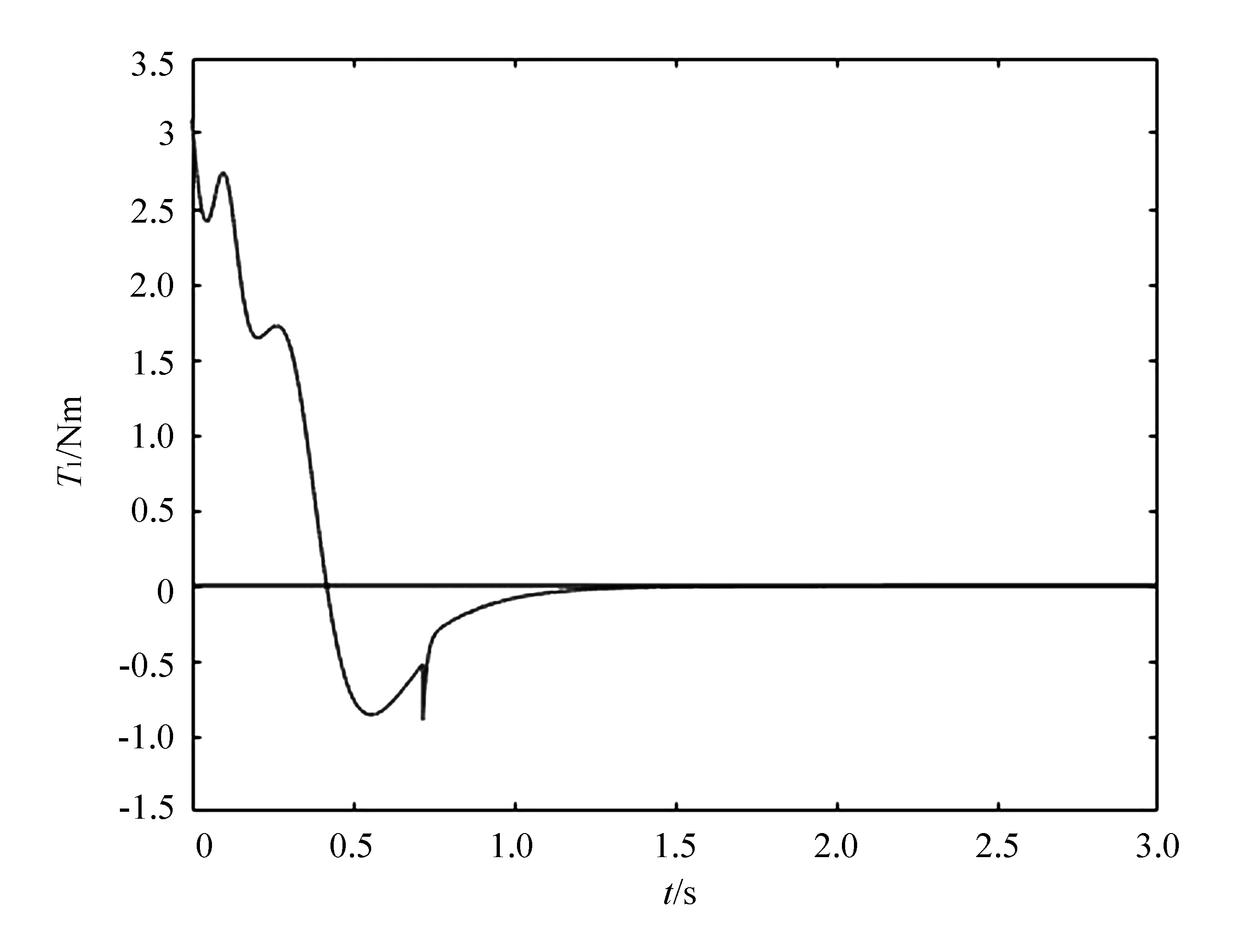
图3 主动臂的力矩

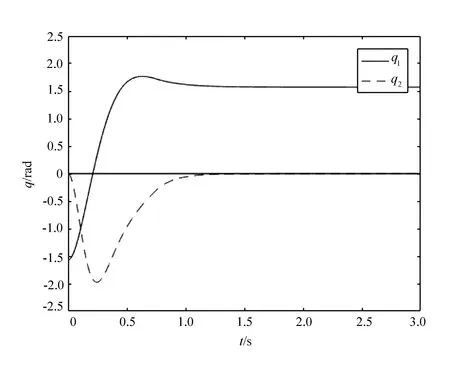
图4 主动臂和欠驱动臂的角度

当采用摆起控制器时,切换信号M为0,当切换为平衡控制器时,切换信号M为1。在Pendubot系统控制中,切换信号如图5所示。图5中,在0.7168 s控制器由摆起控制器切换为平衡控制器,然后一直采用平衡控制器进行控制。

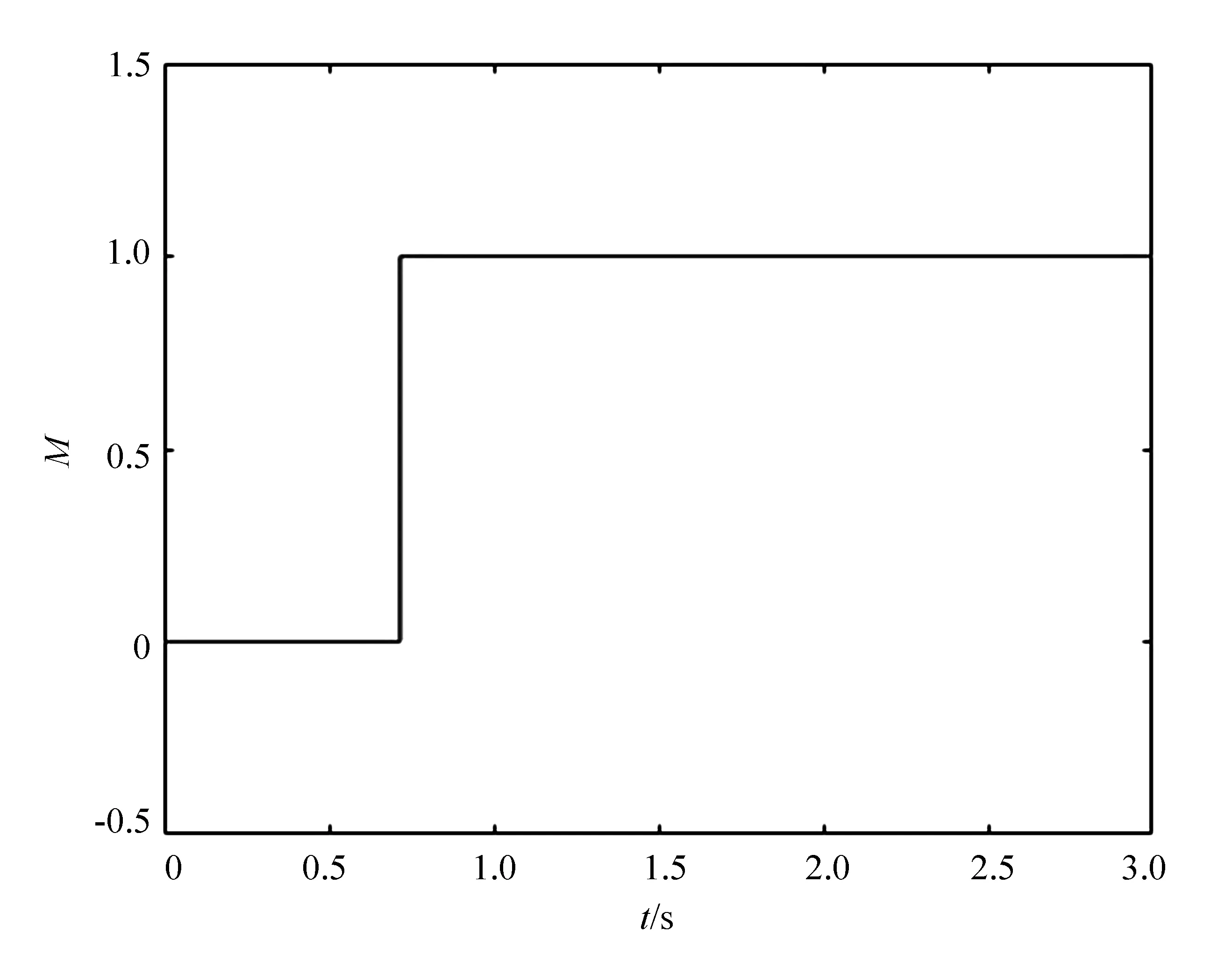
图5 切换信号

5 结语

通过对欠驱动两杆机械臂Pendubot的动力学方程进行分析,采用Matlab/Simulink建立了系统的仿真和控制实验平台,摆起控制采用部分反馈线性化方法,平衡控制采用LQR。利用该仿真平台,可以进行Pendubot系统的控制,有助于学生对欠驱动系统理论的理解,能够提高学生的学习兴趣。学生也可以在该仿真平台上自己编写控制算法,提高实际动手能力和创新能力。

[1] 高丙团,陈宏钧,张晓华.欠驱动机械系统控制设计综述[J].电机与控制学报,2006,10(5):541-546.

[2] Liu Y, Yu H. A survey of underactuated mechanical systems[J].IET Control Theory and Applications,2013,7(7):1-15.

[3] Spong M W. The swing up control problem for the acrobat[J].IEEE Control Systems Magazine,1995,15(1):49-55.

[4] Spong M W, Block D J. The Pendubot: a mechatronic system for control research and education[C]//Proceedings of the 34th Conference on Decision & Control. LA, USA,1995:555-556.

[5] Fantoni I, Loazno R, Spong M W. Energy based control of the pendubot[J].IEEE Transactions on Automatic Control,2000,45(4):725-729.

[6] Xin X, Tanaka S, She J, et al. New analytical results of energy-based swing-up control for the Pendubot[J].International Journal of Non-linear Mechanics,2013,52(3):110-118.

[7] Zhang M, Tarn T J. Hybrid control of the pendubot[J].IEEE/ASME Transactions on Mechatronics,2002,7(1):79-86.

[8] Li W, Tanaka K, Wang H O. Acrobatic control of a Pendubot[J].IEEE Transactions on Fuzzy Systems,2004,12(4):549-552.

[9] 王伟,易建强,赵冬斌,等.Pendubot的一种分层滑膜控制方法[J].控制理论与应用,2005,22(3):417-422.

[10] 牛瑞燕,许午啸,刘金琨.欠驱动机械臂滑膜控制与实验研究[J].仪器仪表学报,2016,37(2):348-355.

[11] Lai X Z, She J H, Yang S X, et al. Comprehensive unified control strategy for underactuated two-link manipulators[J].IEEE Transactions on Systems: Man & Cybernetics Part B: Cybernetics,2009,39(2):389-398.

[12] 蔡自兴.机器人学[M].2版.北京:清华大学出版社,2009.

[13] 薛定宇,陈阳泉.基于MATLAB/Simulink的系统仿真技术与应用[M].2版.北京:清华大学出版社,2011.