基于模态综合法的永磁同步电机动力学分析

卢 鹏，方明霞

(同济大学，上海 200092)

0 引 言

永磁同步电机具有质量轻、效率高、调速范围宽等优点，目前已成为电动汽车中驱动电机的主流。由于车用永磁同步电机的非线性电磁振动对整车的舒适性影响较大，随着电动汽车的发展普及，对车用永磁同步电机振动特性进行研究已引起众多学者的关注。由于电磁转矩波动和电磁径向力波动是引起永磁同步电机振动的主要因素。因此，在分析电机振动时首先需建立电磁力的解析模型。文献[1]针对表贴式永磁同步电机，提出了在外载荷作用下气隙磁密的计算方法，为电磁力的解析模型建立提供了依据；文献[2]对永磁同步电机的径向力波进行分析，发现整数槽电机可有效降低电磁径向力对电机振动的影响；文献[3]根据永磁同步电机电磁场理论，建立了考虑开槽和高次谐波的电磁转矩解析模型，并通过有限元方法进行了验证。永磁同步电机中电磁力的研究为电机动力学特性分析奠定了理论基础。

永磁同步电机属于机电耦合系统，其结构比较复杂，目前对其动力学特性进行研究主要采用有限元法或将其结构进行简化，建立电机低自由度的解析模型。文献[4]采用有限元法对电机的振动特性进行分析，发现电磁力频率接近结构固有频率时对电机振动影响较大；文献[5]采用有限元方法对永磁同步电机在不同结构参数下的电磁振动进行仿真分析，并与实验结果进行对比，两者具有较好的一致性；文献[6]通过有限元仿真得到了不同极槽配合下的振动频谱，仿真结果与实验结果基本一致。有限元法对复杂系统动力学特性进行研究具有较强的实用性，但是无法定性描述系统的动力学行为。为了从机理上研究永磁同步电机的动力学特性，文献[7]将电机定子简化为质量-弹簧-阻尼系统，建立电机振动的理论模型，发现电机振动的频率主要为2倍和6倍的基波频率；文献[8]采用解析方法分析了表贴式永磁同步电机的主要振动频率和振动响应幅值。但是目前电机的解析模型主要将电机作为刚体或取电机的前几阶模态进行分析，刚体或低自由度的简化模型难以准确描述电机机电耦合系统复杂的动力学行为。为此本文将电机分为转子子结构、定子子结构和轴承连接子结构，采用模态综合法建立永磁同步电机机电耦合系统动力学模型，并对其响应特性进行分析。本文研究对永磁同步电机动力学特性的基础研究具有重要的促进作用。

1 永磁同步电机电磁力分析

电磁转矩和电磁径向力主要由定子和转子之间气隙磁场的相互作用产生，是永磁同步电机的主要振动源。电磁转矩波动会引起电机的扭转振动，径向力波动则会引起电机的径向振动。为了建立电机的动力学模型，必须首先得到电磁力的解析模型。

(1)电磁转矩

考虑永磁体磁场为正弦分布，并忽略定子开槽等因素的影响，电磁转矩可表示为如下线性形式[9]：

(1)

式中：p为极对数；ψ1为基波磁链；id，iq分别为d，q轴电流；Ld，Lq分别为d，q轴电感。

考虑定子开槽时，电磁转矩可表示为如下非线性形式[3]：

式中：θ为转子d轴超前A相轴线的机械角度；ψ2k-1为定子的第2k-1阶磁链。

(2)电磁径向力

电磁径向力为定转子单位面积上的电磁压力，其作用于转子、定子上的示意图如图1所示。

(a) 转子电磁径向力

(b) 定子电磁径向力

根据Maxwell应力方程，电磁径向力可表示：

式中:P(α,t)为电磁径向力;B(α,t)和Bt(α,t)为径向和切向气隙磁密;μ0为真空磁导率;α为位置角度;t为时间。

由于径向气隙磁密B一般远大于切向气隙磁密Bt，因此径向力可近似表示为如下非线性形式：

(3)

径向气隙磁密B可采用磁势乘磁导法求得，正弦波供电时：

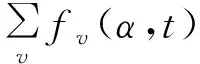
2 永磁同步电机动力学模型建立

永磁同步电机中，扭转振动和径向振动是电机异常噪声的主要原因。本文以某8极24槽永磁同步电机为研究对象，将其分为转子子结构、定子子结构和轴承连接子结构，并将转子作为刚体，定子作为弹性体，采用考虑连接子结构的模态综合法建立电机在电磁转矩和电磁径向力作用下的动力学模型。

2.1 电机结构介绍

表贴式永磁同步电机通常由转子铁心、永磁体、定子铁心和定子机壳组成，转子和定子之间通过轴承连接，其结构示意图如图2所示。

(a)立体图

(b)平面图

电机相关参数如表1所示。

表1 样机参数表

根据永磁同步电机结构形式，将电机分为转子子结构r、定子子结构s和轴承连接子结构o。不考虑连接子结构自重，作用于r和s界面上的连接力用油膜力表示[10]：

(5)

式中：kij为油膜刚度系数，表示j方向的单位位移在i方向产生的作用力；dij为油膜阻尼系数，表示j方向的单位速度在i方向产生的作用力。

2.2 转子动力学模型

(6)

2.3 定子动力学模型

(7)

定子的模态矩阵可由下式得到：

(Ks-λsMs)φs=O

(8)

式中：O为单列零矩阵。

(9)

式中：qs为定子模态坐标。考虑绕组的电机定子前5阶模态频率列于表2，其振型如图3所示。

表2 电机定子的模态频率

(a) 第1阶振型

(b) 第2阶振型

(c) 第3阶振型

(d) 第4阶振型

(e) 第5阶振型

于是定子子结构s在模态坐标下的运动微分方程：

(10)

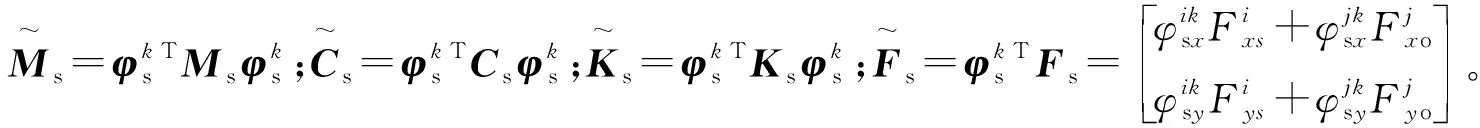
2.4 模态综合法建立电机系统动力学模型

电机系统子结构连接模型如图4所示，不考虑轴承连接子结构的自重，转子子结构受电磁力和轴承连接力的作用，而定子子结构在模态坐标下的运动微分方程中，广义力由电磁力和轴承连接力与振型相乘而得到。

图4 子结构连接模型示意图

电机系统的动力学方程可表示：

(11)

3 永磁同步电机动力学响应分析

3.1 数值方法求解系统动力学响应

(12)

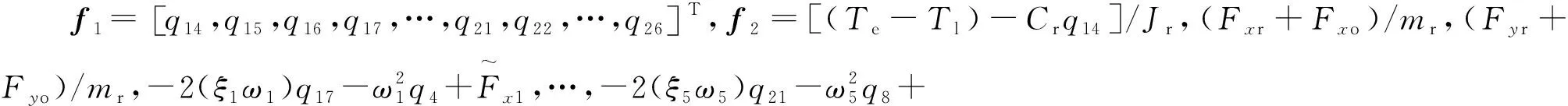
采用数值方法求解系统状态方程，得到转子的位移响应和定子铁心上一节点的位移响应如图5所示。

(a) 转子绕z轴转动角位移

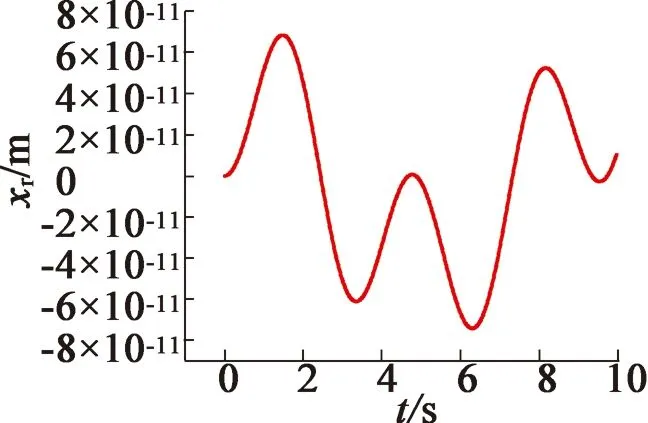
(b) 转子x方向位移

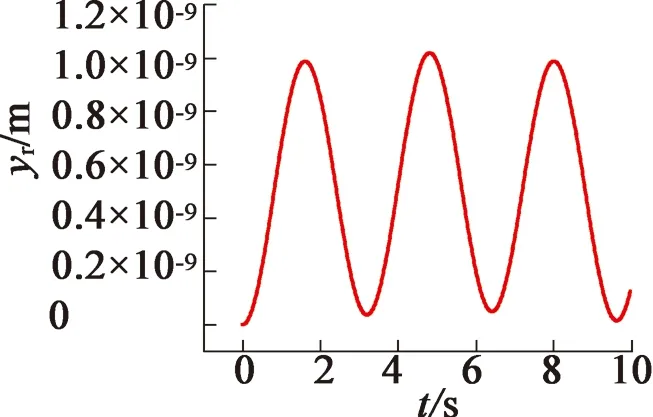
(c) 转子y方向位移

(d) 定子x方向位移

(e) 定子y方向位移

从图5中可以看出，电机转子绕z轴转动的角位移随时间的增加而增大，转子x方向的位移幅度约为-7.41×10-11～6.84×10-11m，y方向的位移幅度约为0～1.02×10-9m。而定子x方向的位移幅度约为-1.79×10-9～-1.37×10-9m，y方向的位移幅度约为1.58×10-9～2.00×10-9m。由于系统中存在非线性电磁转矩和非线性电磁径向力，因此系统的位移响应具有明显的非线性特性。

3.2 有限元方法求解系统动力学响应

为了验证建模方法的正确性，采用有限元法对永磁同步电机的振动特性进行分析。图6为定子的有限元模型。

图6 定子有限元模型

将径向力集中在定子内圈的齿上，通过瞬态分析计算定子的响应特性，图7为定子铁心上同一节点的位移响应曲线。

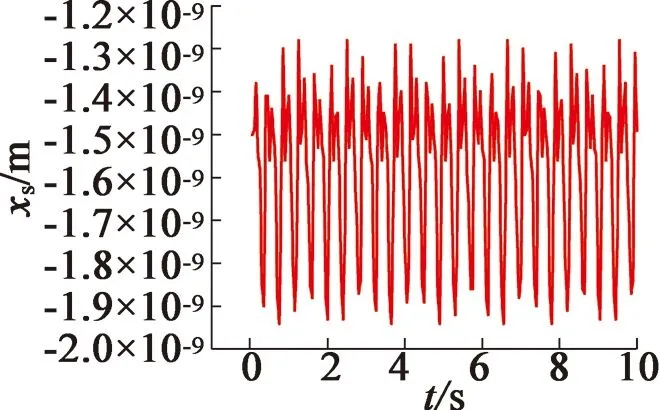
(a) 定子x方向位移

(b) 定子y方向位移

由图7可以看出，定子x方向的位移幅度约为-1.94×10-9～-1.28×10-9m，y方向的位移幅度约为1.49×10-9～2.19×10-9m。

3.3 结果对比

为便于对比，现将解析模型和有限元模型获得的定子铁心上同一节点的位移响应结果列于图8。

(a) x方向位移理论值

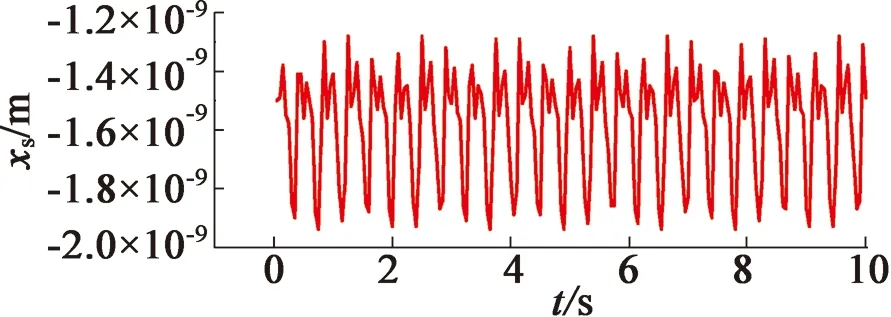
(b) x方向位移有限元值

(c) y方向位移理论值

(d) y方向位移有限元值

从图8中可以看出，对定子铁心上的同一节点，通过求解系统动力学方程和有限元法得到的x方向位移响应的最大值相差6.57%，最小值相差8.38%；y方向位移响应的最大值相差9.50%，最小值相差5.70%。误差均小于10%，满足工程要求。

4 不同参数对定子动力学响应的影响

上节研究表明，采用模态综合法建立电机的动力学模型具有足够的精度，现采用式(11)分析不同参数下电机的动力学特性，给出不同参数的取值原则。

4.1 气隙长度的影响

作用于电机定转子上的电磁力主要通过气隙磁场产生，为了分析不同气隙长度下电机的动力学响应，针对上述电机改变永磁体厚度从而改变气隙长度，得到气隙长度g∈(0,2 mm)时定子的加速度响应。图9给出g=0.001 m时定子节点的最大加速度响应，不同气隙长度下定子节点的最大加速度如图10所示。

(b) y方向加速度

图10 不同气隙长度下定子节点的最大加速度

从图10可以看出，在不改变定转子结构尺寸的情况下，增加气隙长度，定子的最大振动加速度也会增大。所以为了减小定子的振动加速度，在结构参数满足其他要求的情况下，应尽量减小电机的气隙长度。

4.2 极弧系数的影响

图11 不同极弧系数下定子节点的最大加速度

由图11可知，通过改变极弧角的方式改变电机的极弧系数时，定子的最大振动加速度会随着极弧系数的增加而增大。因此为了减小定子的振动加速度，电机的极弧系数应在满足结构其他要求的情况下尽量取较小值。

5 结 语

根据引起电机振动的主要因素，本文首先对电磁转矩和电磁径向力进行了分析，其解析模型具有非线性特性。然后建立了电机在电磁转矩和电磁径向力作用下的动力学方程。由于定子的径向振动是电机噪声的主要振源，所以将定子作为弹性体，利用模态综合法缩减自由度，建立了定子在模态坐标下的动力学模型。

由于系统的动力学方程是复杂的非线性方程，从理论上求解比较困难，本文通过数值方法求解得到系统的振动响应。利用有限元软件模拟定子在电磁径向力作用下的振动，得到的位移响应结果与理论方法得到的结果误差较小，可满足工程应用要求。

对于工程上比较关心的结构加速度响应，本文分别改变电机的气隙长度和极弧系数计算得到不同参数下定子x，y方向的加速度响应。从加速度响应结果可以看出，定子的最大振动加速度会随着气隙长度和极弧系数的增加而增大。所以为了减小电机的振动加速度，在电机结构满足要求的情况下，应尽量减小电机的气隙长度和极弧系数。

[1] ZHU Z Q,HOWE D.Instantaneous magnetic field distribution in brushless permanent magnet dc motors,part IV:magnetic field on load[J].IEEE Transactions on Magnetics,1993,29 (1):152-158.

[2] 刘景辉,黄开胜,陈治宇,等.永磁同步电动机径向电磁力的分析[J].微特电机,2013,41(5):16-18.

[3] 马琮淦,左曙光,孟姝,等.考虑开槽和高次谐波的永磁同步电机解析模型[J].振动、测试与诊断,2015,35(2):231-237.

[4] ISHIBASHI F,NODA S,MOCHIZUKI M.Numerical simulation of electromagnetic vibration of small induction motors[J].IEE Proceedings of Electric Power Applications,1998,145(6):528-534.

[5] 杨浩东.永磁同步电机电磁振动分析[D].杭州：浙江大学,2011.

[6] SUN T,KIM J M,LEE G H,et al.Effect of pole and slot combination on noise and vibration in permanent magnet synchronous motor[J].IEEE Transactions on Magnetics,2011,47(5):1038-1041.

[7] 李良,蒋宇晨.三相交流永磁同步电动机电磁振动的理论建模与分析[J].机械强度,2016(1):27-31.

[8] HAUNG S,AYDIN M,LIPO T A.Electromagnetic vibration and noise assessment for surface mounted PM machines[C]//Proceedings of IEEE Power Engineering Society Summer Meeting,2001,03; 1417-1426.

[9] 唐任远.现代永磁电机理论与设计[M].北京：机械工业出版社,2016:247.

[10] 虞烈,刘恒.轴承-转子系统动力学[M].西安：西安交通大学出版社,2001:80.