地图综合中几何相似性的度量*

刘 杨，张晶莹

(湖南都市职业学院，湖南 长沙 410137)

地图综合通过简化地图数据的表达以适应较小比例尺和满足地图易读性的需要，如何评估和保证综合后的地图的质量，成为当代数字制图需要解决的一个主要问题.综合评价方法分为定性和定量2种.一般来说，大部分的研究都是针对地图综合前后的几何或拓扑关系的变化进行定性分析，很少采用定量的评价方法对目标之间的关系进行度量.[1]笔者拟引入传统的空间目标距离、Hausdorff距离、对称差面积、旋转函数距离和曲面距离等5个几何属性指标来分析不同比例尺综合地图的面目标的几何属性变化，并通过度量地图的几何相似性来分析综合地图的质量.

1 几何相似性度量指标

1.1 传统的空间目标距离

图1 最小距离、最大距离和质心距离Fig. 1 Minimum,Maximum and Centroid Distance

在二维地理信息空间(GIS)中，设2个点的坐标分别为pi(xi1,xi2)和pj(xj1,xj2)，则2个点之间的距离为

(1)

1.2 豪斯多夫距离

点集A和B的Hausdorff距离可以描述为[2]

(2)

其中：sup(·)表示集合的最小上界；inf(·)表示集合的最大下界；‖·‖表示2点之间的某种度量；h(A，B)和h(B，A)分别为从A到B和从B到A的有向Hausdorff距离.(2)式中2个有向距离函数的结果通常不一致，也就是不符合距离度量的对称性，所以不是真正的距离度量.由于地理信息空间的目标是不为空的集合(即有界闭集)，因此有向Hausdorff距离可以描述为[3]

同样地，Hausdorff距离还可以描述为

(3)

从(3)式可知Hausdorff距离也是一种最大-最小距离.假设A和B的Hausdorff距离为d0，那么A(或B)到B(或A)的最小距离不大于d0.同样地，对于A(或B)的任意一个点pA(或pB)，一般都可以在B(或A)上找到一个点位于pA(或pB)的d0邻域(以pA(或pB)为中心，以d0为半径的一个圆)内.因此Hausdorff距离和2种有向Hausdorff距离可以使用一个基于缓冲区的方法来定义和计算.基于缓冲区方法的Hausdorff距离如图2所示，其计算公式为

其中⊕表示数学形态学的膨胀算子，为Minkowshi度量和运算[4].

图2 基于缓冲区方法的Hausdorff距离Fig. 2 Hausdorff Distance Based on Buffer Method

1.3 对称差面积

计算2个面目标之间对称差的面积也是一种很好的度量方法，它可以忽略目标局部的不同之处(如凹陷和尾部).该度量方法可描述为[5]

Area(A，B)=‖AΔB‖=A∪B-A∩B，

其中Δ是对称差算子，Area(·)是用来计算面积的函数.A Galton[6]指出面目标之间面积的对称差可以很好地度量2个面目标之间的分离性和相似性(或差异性).Hausdorff距离不适用的3种情形如图3所示，面目标间对称差的面积如图4所示.图4中阴影部分表示图3中面目标A和B之间面积的对称差，图4c中A和B之间的差异最大.

图3 Hausdorff距离不适用的3种情形Fig. 3 Three Cases Unsuitable for Hausdorff Distance

图4 面目标间对称差的面积Fig. 4 Separation of Regions Measured by Area of Symmetric Difference

对称差面积计算出来后，可用指标α来度量2个目标之间的相似性，即

(4)

由(4)式可知，α越接近于1，2个目标的相似度越高.

1.4 旋转函数距离

旋转函数也被称为角度计算函数，是用于多义线或多边形之间进行匹配的一种距离函数.利用旋转函数表达多义线的结果如图5所示.由图5可知，曲线A可以按照如下方法定义：(1)Y轴代表曲线与左转切线之间的夹角.如果曲线的边向左转就在原来的角度上加上旋转角；如果曲线边向右转就在原来的角度上减去旋转角.(2)X轴代表弧线的长度.(3)曲线表示θA(s).由此可知，旋转函数不会随曲线(或多边形)的平移而发生变化.综上所述，旋转函数间的距离可表示为[7]

其中p的取值通常为2.利用旋转函数间的距离可以表示不同曲线间的差异,这个距离指标可用于相同(或近似)比例尺的同名线或多边形的相似性度量.A和B之间的差异的度量结果如图6所示.

图5 旋转函数表达的多义线Fig. 5 Representation of Poly-Line by Turning Function

图6 A和B之间的差异的度量结果Fig. 6 Difference Between A and B Measured by Turning Function Distance

定义2个目标的形状相似度为

(5)

其中：Area(Oi)是匹配后2幅图形没有重叠的面积；Area(TFi,A)是旋转变换下目标A的面积；Area(TFi,B)是旋转变换下目标B的面积.A,B2个目标的相似性度量结果如图7所示.

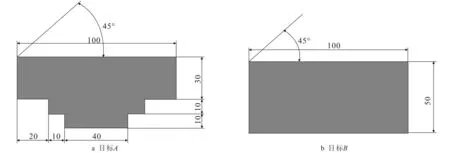
图7 目标的相似性度量结果Fig. 7 Similarity Measures of Goals

图8 旋转变换下的A和BFig.8 Object A and B by Turning Function Distance

在旋转变换下建立的直方图如图8所示.图8中横轴表示图形边界的长度l，纵轴表示图形边界方向与基准线的角度β(图形边界顺时针).由图8可以看出,2个直方图叠加后产生的阴影面积就是匹配之后2幅图形没有重叠的面积.根据(5)式计算2个目标的形状相似度,

1.5 曲面距离

曲面距离可用来度量2个目标之间的差异程度，其定义为[8]

其中：A和B是2个多边形目标；Area(A∩B)是目标A与B交集的面积；Area(A∪B)是目标A与B并集的面积.ω(A，B)∈[0,1]，其值越接近0，说明2个不同比例尺下的同一区域图形的相似度越高.

2 面目标几何相似性度量方法

2.1 实验设计与实现

同一个地区、不同比例尺的2幅森林专题地图如图9所示.图9a的比例尺为1∶25 000，进行地图综合后得到图9b，其比例尺为1∶50 000.在图9a上有33个面目标，在图9b上有16个面目标.在此例中，综合操作使用合并来删除小的多边形，分别应用5个几何相似性度量指标来计算图形的相似度，并给出最终的结果.

应用二次开发控件(MapObjects)在VB中计算2个面目标间的几何相似度,操作界面如图10所示.几何相似度的计算流程为:叠加2种比例尺的地图，再分别采用5种计算方法逐一计算地图上的面目标.不同度量方法得到的计算结果列于表1.

图9 不同比例尺的森林专题地图Fig. 9 Forest Thematic Maps with Different Scales

图10 面目标几何相似性度量方法实现Fig. 10 Implementation of Measure Approaches of Geometric Similarity Between A and B

几何相似性 度量方法 面目标1234567Dmax(A,B)184.421 4237.098 8243.692 472.007 765.258 898.989 1103.631 5Dmin(A,B)7.340 91.659 33.663 91.956 41.790 81.773 32.612 9Dc(A,B)0.852 12.264 13.996 62.064 42.220 54.391 53.534 8H(A,B)8.425 33.203 149.547 82.467 23.847 45.561 54.455 5α0.971 80.957 40.889 70.880 90.820 40.772 10.888 8SS(Oi)0.696 90.374 60.383 90.863 40.955 10.389 30.879 8ω(A,B)0.027 90.041 60.036 30.113 20.161 80.211 70.105 2几何相似性 度量方法 面目标891011121314Dmax(A,B)62.443 6171.089 566.462 7229.788 6112.026 4190.316 568.355 1Dmin(A,B)1.114 22.617 62.428 40.904 82.744 63.482 24.352 3Dc(A,B)2.427 93.790 43.079 95.136 44.652 04.829 55.160 5H(A,B)3.726 24.178 53.416 614.159 46.108 15.412 45.436 8α0.862 50.700 10.831 00.708 70.864 50.869 00.657 7SS(Oi)0.940 20.250 70.413 60.656 30.973 70.975 20.940 9ω(A,B)0.126 20.260 80.153 80.246 80.126 30.122 90.286 8

2.2 结果比较

对实验结果进行分析可知：最大、最小距离度量的是综合前后同一目标的最大、最小距离，根据不同的需要可以计算不同区域面目标的最大、最小距离；Hausdorff距离适用于度量面目标的分离性，在度量空间目标的形状方面，Hausdorff距离和旋转函数距离可以有效地度量空间目标整个形状的变化，而最小距离、最大距离、质心距离、曲面距离和对称差面积相对差一些；采用对称差面积能较好地度量2个面目标的差异性且便于计算，指标α的值越接近1，表明2个面目标相似度越高；旋转函数度量比较适用于多边形相似性度量，旋转函数距离度量中SS(Oi)∈[0,1],其值越接近1，说明2个目标几何形状相似度越大；曲面距离度量中ω(A，B)∈[0,1]，其值越接近0，说明2个目标的面积相似度越大，综合前后面积变化越小.根据表1可以认为:当ω(A，B)≤0.2时，判定综合效果较好；当0.2<ω(A,B)<0.5时，判定综合效果较差；当ω(A,B)≥0.5时，判定综合效果很差.

参考文献：

[1] WEIBEL R,DUTTON G.Constraint-Based Automated Map Generalization[C].Proceedings of the 8th Spatial Data Handling Symposium.Vancouver,1998:214-224.

[2] HUTTENLOCKER D P,KLANDERMAN G A,RUCKLIDGE W J.Comparing Images Using the Hausdorff Distance[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1993,15(9):850-863.

[3] DENG M,LI Z,CHEN X.Extended Hausdorff Distance for Spatial Objects in GIS[J].International Journal of Geographical Information Science,2007,21(4):459-475.

[4] SERRA J.Image Analysis and Mathematical Morphology[M].New York:Academic Press,1982.

[5] ALT H,FUCHS U,ROTE G,et al.Matching Convex Shapes with Respect to the Symmetric Difference[J].Algorithmica,1998,21(1):89-103.

[6] GALTON A.Continuous Change in Spatial Regions[C].Spatial Information Theory a Theoretical Basis for GIS:International Conference COSIT '97 Laurel Highlands.Pennsylvania,USA,1997:1-13.

[7] LATECKI L J,LAKAMPER R.Shape Similarity Measure Based on Correspondence of Visual Parts[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2000,22(10):1 185-1 190.

[8] VAUGLIN F,BEL HADJ ALI A.Geometric Matching of Polygonal Surfaces in GIS[C].Proceedings of the ASPRS-RTI.Tampa,Floride,USA,1998:1 511-1 516.