具恢复机制的相依电力-信息网络连锁故障传播*

谭 鑫，罗研彬

(湖南大学电气与信息工程学院,湖南 长沙 410082)

近些年来，随着电力系统和信息网络技术的不断发展，电网的复杂结构特性对连锁故障反应的影响越来越受到关注.连锁故障的产生严重阻碍电力网络的发展，因此国内外学者[1-2]应用复杂网络理论对电网安全开展了研究.随着电力信息系统的节点不断增多，覆盖面逐步增大，电力信息网络也发展成一个复杂网络，其网络拓扑的统计特性表现出复杂网络的一般特征.信息系统与一次电网的深度融合带来了新的脆弱性因素，单侧系统的故障有可能通过系统间的耦合在网间产生交互传播的连锁故障，从而扩大停电规模[3-6]，连锁性故障的迅速传播最终导致电网的大面积崩溃.

网络相依性和相依网络研究已经成为当代复杂网络领域的热点问题.以往电力系统一次网络和电力信息网络的研究工作基本上是分开的，并没有考虑2个复杂网络之间的交互影响.V Rosato等[7]对意大利电力网络和数据采集与监视控制(SCADA)系统的相互影响进行了建模，电力网络节点依靠信息网络节点进行控制，信息网络节点需要电力网络节点提供电力支持；R Albert等[8]对2个相互依赖的无标度网络的连锁故障过程建立模型，发现2个无标度网络由于相互依赖的特性，对随机攻击表现出很强的脆弱性,但是单个无标度网络对随机攻击有较强的鲁棒性；S V Buldyrev等[9]从复杂网络视角，研究了信息网与电力网间的相互依存关系造成的智能电网连锁故障.目前，对电网连锁故障的传播机理主要从复杂网络理论和连锁故障模型这2个方面进行研究.文献[10-12]分别验证了美国西部电网、中国北方电网和中国华东电网等具有小世界网络特性,认为小世界特性造成了电网连锁故障的迅速扩张.学者们运用复杂科学理论研究连锁故障发生的原因和机理，弥补了运用传统还原论[13]研究电力网络的不足,同时提出了OPA模型、CASCADE模型、分支过程模型、Motte-Lai模型和有效性能模型[14]等，取得了满意的效果.基于相依网络已有的研究成果，笔者将运用图论数学工具对电力网和信息网进行一体化建模，并以此统计电力网和信息网的复杂网络特征参数，从而判定它们是否均具有小世界和无标度特性；在建立相依电力-信息网络连锁故障模型后，提出具有恢复机制的相依网络连锁故障传播模型，并通过依赖性恢复策略来研究相依网络连锁故障的传播.

1 电力-信息相互依存网络的建模和复杂网络特性

1.1 电力网和信息网一体化建模

为了定量分析电力网和信息网，先对二者作如下假设：

(1)考虑电力网和信息网中节点的异质性，将电力系统中的发电站和变电站分别等效为发电站节点和变电站节点，将信息系统中省级调度中心、地级调度中心和各电力站点对应的信息系统分别等效为省调节点、地调节点和信息节点.

(2)将电力系统中的输电线路等效为电力网的边，将信息系统中的通信线路等效为信息网的边，忽略线路的差异且认为所有边都是无向边.

(3)不考虑多重边和自环，忽略设备和线路的容量.

图1 IEEE300节点系统及其340节点信息网网络结构Fig. 1 IEEE300 Node System and Its Network Structure of 340 Node Information Network

基于以上假设，电力网和信息网可分别建模为无权无向图.电力网和信息网的网络结构如图1所示.电力信息-物理系统的电力网选取IEEE 300节点系统，信息网采用双星型结构[15].双星型结构采用分层设计：核心层为一个省调节点和一个备调节点直接相连；骨干层为38个地调节点，每个地调节点都双归到省调节点和备调节点；接入层为69个发电站信息节点和231个变电站节点，各发电站信息节点双归到所属地调节点和省调节点，各变电站单归到所属地调节点.

1.2 电力-信息网络小世界和无标度特性判定

小世界特性是指网络同时具有较大聚类系数和较小平均距离的特点，Watts将如下网络拓扑特征定义为小世界特性：

(1)

其中：下标random表示随机网络；C为聚类系数；L为网络的平均距离；Crandom表示与小世界网络具有相同节点数和平均度数的随机网络的聚集系数；Lrandom表示与小世界网络具有相同节点数和平均度数的随机网络的特征路径长度.

Crandom≈k/N,Lrandom≈lnN/lnk.

(2)

这里：N为网络中的节点数；k为平均度数，即每个节点连接边数的平均值，它反映了网络的强度，k=2M/N,M为网络中的边数.

小世界网络介于规则网络和随机网络之间，其特性是以概率p引入极少量远程连接.相对于具有相同节点数和边数的规则网络，这些极少量的远距离连接使小世界网络节点间的平均距离明显减小，从而形成了小世界网络中攻击行为快速远程传播的关键连接和相应的动态特性.此外，对上述远程连接的攻击，可能导致整个网络连通性的剧烈变化.

常用的统计特征参数指标有节点数N、边数M、节点度数k、平均度数k、特征路径长度L和聚集系数C等.具体的参数定义可以参考文献[5].电力网和信息网的统计特征参数列于表1.根据(1)，(2)式和表1中所列的参数值可判定IEEE300节点电力网及其340节点信息网均具有小世界特性.

表1 相依网络模型中电力网和信息网拓扑统计特征参数

无标度特性是指网络中度分布和演化规律的统计特性相对于概率而遵循某种幂指数的形式，缺乏某一特征尺度，在双对数坐标系下近似于直线.网络的度分布对网络结构具有重要的影响，随机网络对随机攻击和蓄意攻击都表现出较强的鲁棒性，无标度网络在随机攻击下表现出较强的鲁棒性，而在蓄意攻击下十分脆弱.

图2 电力网和信息网模型的节点度数累积分布Fig. 2 Cumulative Node Degree Distributions in the Models of Power Grid and Cyber Network

由图2可知，相依网络模型中电力网和信息网不符合标准的无标度网络特征，但是具有无标度网络的特点：大量的低度数节点和少量的高度数节点，且度分布概率随度数的增加而急剧减小.大量低度数节点的存在对维持网络的连通性及传输能力具有消极的影响，因此应考虑对该类型节点进行改造.

采用最小二乘法拟合曲线分别得到电力网和信息网的累积度分布表达式为

P(K≥k)=1.101k-1.097，

(3)

P(K≥k)=0.990k-1.516.

(4)

由(3)，(4)式可知，电力网和信息网皆符合高斯分布，2个网络在度分布上具有一定的相似性.

2 连锁故障建模

本研究所考虑的耦合相互依存网络是由电力网P和信息网C2个独立的子网络组成的.2个子网络可以分别表示为无权无向图GP和GC，GP=(VP,EP),GC=(VC,EC)，其中VP和VC分别是电力网和信息网的节点集，EP和EC分别是电力网和信息网的内连通边的集合.这里，每个子网络的耦合依赖边集可以相应地定义为EPC={(u,v)|u∈VP,v∈VC}，称EPC为网络的外部依赖边.电力网P和信息网C之间的外部依赖边边缘随机耦合，确保在网络P和网络C中的任何节点都有连接到相互依存网络的外部连接边.假设电力网和信息网有相同数量的节点，即NP=NC，子结构具有相同的拓扑结构，笔者分别考虑了WS小世界网络、BA无标度网络和ER随机网络3种网络的情况.

WS小世界网络介于规则网络和随机网络之间，它是通过2个步骤建立的：(1)从最近的具有N个节点数的耦合网络开始，每个节点连接到k个最近的节点;(2)每条边以概率q被随机地切割和重新连接，但必须确保网络中不存在自循环和多重边.在WS小世界网络中，参数q代表网络随机化的程度，不同的重连接概率代表不同的网络.规则网络、WS小世界网络和ER随机网络的建立过程如图3所示.

图3 规则网络、WS小世界网络和ER随机网络的建立过程Fig. 3 Construction Courses of WS Small-World Network and ER Random Network

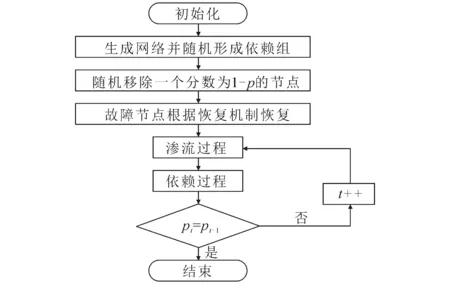
在建立WS小世界网络时令概率q=0.5，在建立ER随机网络时令概率q=1，且WS小世界网络和ER随机网络的平均度为k.BA无标度算法的构造主要分为2步：(1)增加节点.从m0个初始节点开始，每个时间节点网络都会导入一个新的节点，并连接到m(m

3 具有恢复机制的级联失效

3.1 具有恢复机制的故障传播模型

笔者提出了一种新的级联过程模型来研究具有恢复机制的网络故障传播.设G(N,A)为一个网络，其中:N表示节点集;A代表连接集，A=(i,j)|ai,j=1.若从节点i到j的连接存在，则|A|=m,ai,j=1;若连接不存在,则有ai,j=0.一个网络中拥有分数q的节点能够随机选择形成大小为g的依赖组，而拥有分数(1-q)的其他节点不属于任何依赖组.首先通过随机删除分数为(1-p)的节点和连接边使得相依网络的级联失效，初始删除完成后，采用以下3种恢复机制使故障点恢复到正常状态：(1)随机恢复(RR).故障节点以概率γ恢复.(2)目标恢复(TR).故障节点以τ的最大值为概率高度恢复.(3)依赖性恢复(DR).依赖组中的故障节点，其中小于或等于依赖恢复阈值gR的部分节点将恢复正常，而没有恢复的故障节点将在网络中进行渗流过程和依赖过程.渗流过程中，故障节点通过连接边可能导致其他节点从网络上断开；依赖过程中，当依赖组中的部分故障节点等于或大于依赖失效阈值gF时，即使它们仍然通过连接边连到网络，该组中的所有的节点也将发生故障.

3.2 级联过程

图4 具有恢复机制的级联失效仿真流程Fig. 4 Flow Chart for Simulating Cascading Failure with Recovery Mechanism

具有恢复机制的级联失效仿真流程如图4所示.由图4可知，在生成网络G(N,A)之后，网络随机形成依赖组.为了简便起见，本实验通过随机选择节点的方式来形成依赖组，这有助于级联故障的理论分析.初始删除分数为1-p的节点，由恢复机制恢复故障节点.对于依赖机制，这个恢复过程可以用以下关系来描述：

(1)若pg≤gR，依赖性恢复,其中pg是依赖组中的一部分故障节点.

(2)若pg>gR,依赖过程和渗流过程迭代地发生.依赖过程中若出现pg≥gF，则依赖性失效.

3.3 具有恢复机制的模型分析

在笔者提出的模型中，提供了3种恢复机制(DR，RR和TR)将已移除的节点恢复到正常状态.BA和ER网络在不同gF和恢复机制下的恢复效果如图5和图6所示.

图5 BA网络在不同阈值gF和恢复机制下的恢复效果Fig. 5 Recovery Mechanisms for a BA Network with Different gF

图6 ER网络在不同阈值gF和恢复机制下的恢复效果Fig. 6 Recovery Mechanisms for a ER Network with Different gF

由图5和图6可以看出：对于BA和ER网络，目标恢复机制与随机恢复机制具有非常相似的恢复级别；依赖恢复机制可以使网络更健壮，这种优势随着失效阈值gF的减少而提高.对于恢复机制，笔者专注于相依网络的故障传播.

级联过程结束时，巨型组件的分数、故障节点与恢复节点的数量差异分别为

(4)

ΔFR=(p+NR)G0(1-P-NR)+1-pF-NR.

(5)

根据(4)式可知，依赖组的大小在网络的渗流过程中起着重要作用,因此，笔者着重研究依赖组的大小对网络中故障传播的影响.由于故障的传播，在初始节点发生故障后通过渗流过程和依赖过程，初始故障会引起更多的节点发生故障.然而，在级联过程中，许多故障节点可以通过恢复机制恢复到正常状态.总的来说，在初始故障之后，故障节点与恢复节点的数量差异ΔFR决定了网络的鲁棒性.仿真实验结果表明，恢复过程完成之后级联过程仅存在渗流过程和依赖过程；拥有大的故障阈值的网络能够承受更多的故障节点，相应网络的鲁棒性更好;网络的恢复阈值越小，故障节点能够恢复到正常状态的节点分数也越小.网络在不同的gF和gR下的鲁棒性如图7所示,由图7可知，拥有更大故障阈值的网络更加健壮，而恢复阈值越小则网络越脆弱.

图7 网络在不同gF和gR下的仿真结果Fig. 7 Simulation Results of an Network with Different gF and gR

4 结语

本相依网络连锁故障传播模型研究结果表明:目标恢复机制与随机恢复机制具有非常相似的恢复级别,依赖恢复机制比目标恢复机制和随机恢复机制的恢复级别更高，且这种优势随着失效阈值gF的减少而提高;恢复过程完成之后级联过程仅存在渗流过程和依赖过程，依赖组的大小在网络的渗流过程中起着重要的作用;拥有更大故障阈值的网络更加健壮，反之恢复阈值越小则网络越脆弱.

参考文献：

[1] WATTS D J.Small Worlds:The Dynamics of Networks Between Order and Randomness[J].Physics Today,2000,53(11):54-55.

[2] 于 群,郭剑波.中国电网停电事故统计与自组织临界性特征[J].电力系统自动化,2006,30(2):16-21.

[3] VESPIGNANI A.Complex Networks:The Fragility of Interdependency[J].Nature,2010,464(7291):984-985.

[4] 郭庆来，辛蜀骏，孙宏斌，等.电力系统信息物理融合建模与综合安全评估：驱动力与研究构想 [J].中国电机工程学报，2016，36(6)：1 481-1 489.

[5] 谭玉东，李欣然，蔡 晔，等.基于电气距离的复杂电网关键节点识别 [J].中国电机工程学报，2014,34(1):146-152.

[6] BOBBIO A,BONANNI G,CIANCAMERLA E,et al.Unavailability of Critical SCADA Communication Links Interconnecting a Power Grid and a Telco Network[J].Reliability Engineering & System Safety,2010,95(12SI):1 345-1 357.

[7] ROSATO V,ISSACHAROFF L，TIRITICCO F,et al.Modelling Interdependent Infrastructures Using Interacting Dynamical Models[J].International Journal of Critical Infrastructures,2008(4):63-79.

[8] ALBERT R,JEONG H,BARABSI A L.Error and Attack Tolerance of Complex Networks[J].Nature,2000,406：378-382.

[9] BULDYREV S V,PARSHANI R,PAUL G,et al.Catastrophic Cascade of Failures in Interdependent Networks[J].Nature,2010,464:1 025-1 028.

[10] WATTS D J,STROGATZ S H.Collective Dynamics of "Small World" Networks[J].Nature,1998,393(4):440-442.

[11] 孟仲伟，鲁宗相，宋靖雁.中美电网的小世界拓扑模型比较分析[J].电力系统自动化，2004，28(15):21-29.

[12] 丁 明，韩平平.基于小世界拓扑模型的大型电网脆弱性评估算法[J].电力系统自动化，2006，30(8)：7-10.

[13] COSTA L D F,OLIVEIRA O N,TRAVIESO G,et al.Analyzing and Modeling Real-World Phenomena with Complex Networks:A Survey of Applications[J].Advances in Physics,2011,60(3):329-412.

[14] 董政呈，方彦军，田 猛.不同耦合方式和耦合强度对电力-通信耦合网络的影响[J].高电压技术，2015，41(10)：3 464-3 469.

[15] 胡 娟，李智欢，段献忠.电力调度数据网结构特性分析[J].中国电机工程学报,2009,29(4):53-59.