基于改进的分形插值与SVM的股指预测模型*
黎 红,王宏勇
(南京财经大学应用数学学院,江苏 南京 210023)
分形理论的创始人B B Mandelbrot[1]在研究股票价格时间序列的波动规律时发现,股票价格序列呈现尖峰胖尾的统计特征,不服从正态分布,因此提出用分形分布来描述股票收益序列.研究[2-5]表明,金融市场的波动具有明显的非线性分形特征.将分形的理论和方法与某些统计分析模型或者数据挖掘技术相结合,成为研究现代金融市场的非线性范式.[6-9]在分形分析方法中,基于迭代函数系理论发展起来的分形插值技术是拟合数据的新方法[10],它尤其适合应用于研究非平稳数据和非光滑曲线的逼近、拟合及趋势预测[11-12].在利用分形插值方法对数据进行拟合和预测时,分形插值迭代函数系的一组自由参数——纵向尺度因子,对于拟合效果具有决定性的影响.翟明岳[13]令所有的纵向尺度因子都相等,再利用数据序列的分形维数或者Hurst指数求出这些相等的纵向尺度因子.当然,也有其他求纵向尺度因子的方法[14],但是计算非常复杂.此外,利用分形插值进行预测时,对于最后一个预测值常常需要先给出期望值,然后利用外推法来确定其他预测点的值.因受到预先给定的期望值的影响,这些预测值的精确性难以保证.近年来,支持向量机(Support Vector Machine,SVM)越来越多地被应用于金融时间序列的预测[7,15-18].SVM是一种基于统计理论发展起来的数据挖掘方法,在求解小样本、非线性和高维模式识别问题时有优势;但是在多目标预测和实时控制方面能力欠缺,每次仅能预测1个值.针对在选取纵向尺度因子时遇到的这些问题,笔者提出一种确定纵向尺度因子的新方法,并在此基础上建立一个改进的分形插值模型,将该模型与SVM模型相结合,形成混合预测模型.
1 时间序列的R/S分析方法与SVM预测模型
1.1 R/S分析方法
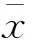
1.2 SVM预测模型
SVM预测模型的基本思想是,通过非线性映射φ将样本数据xi映射到高维特征空间,并在该空间进行线性回归.设训练样本集为{(xi,yi),i=1,2,…,l},则回归模型为f(x)=(ω·φ(x))+b,对应的优化问题为:


在构建SVM预测模型时需选取惩罚参数和核函数,这2个参数的选取直接影响模型预测的精度.本研究取径向基核函数K(xi,x)=exp(-γ‖xi-x‖2),在LIBSVM仿真平台上实现SVM算法.
2 基于改进的分形插值与SVM的混合预测模型
对于区间I=[a,b],给定划分Δ={x0,x1,…,xN},满足a=x0 (1) 满足端点条件 (2) 由(1),(2)式可得: (3) (4) 由上述可知,当插值点{(xi,yi):i=0,1,…,N}给定且纵向尺度因子di(i=1,2,…,N)确定时,可由(3)式求得相应的系数ai,ci,ei,fi(i=1,2,…,N),迭代函数系也就确定了.因此,如何确定自由参数di是确定迭代函数系的关键.以往一种简单的做法是令所有的di都相等,先求出Hurst指数,再利用(4)式来计算di.但通过这种方法确定的di和由此得到的分形插值曲线,在实际应用中拟合效果不佳.为了提高分形插值的拟合精度,笔者根据数据的自身信息提出一种确定di的新方法. 对于数据集{(Xi,Yi),i=0,1,…,m},从中等距或非等距地选取插值点{(Pj,Qj),j=0,1,…,k},k {(Pj-1,Qj-1),(Xl,Yl),(Xl+1,Yl+1),…,(Xl+n,Yl+n),(Pj,Qj)}, 则这些数据点之间的高度差 dj0=Yl-Qj-1,dj1=Yl+1-Yl,…,dj,n+1=Qj-Yl+n. 记 djmax=max(Qj-1,Yl,Yl+1,…,Yl+n,Qj),djmin=min(Qj-1,Yl,Yl+1,…,Yl+n,Qj). 令 (5) 按照(5)式确定的di,能够将相邻插值数据之间的局部变化趋势和整体变化幅度考虑在内,且满足条件|di|<1,这使得所构造的分形插值函数在局部更逼近原始数据. 接下来建立基于改进的分形插值与SVM的混合预测模型.对于已知数据{(Xi,Yi),i=0,1,…,m},假设已选取插值点为{(Pj,Qj),j=0,1,…,k},并由(5)式求得dj(j=1,2,…,k),现需要预测未来数据{(Xi,Yi),i=m+1,m+2,…,m+r}.由于有r个未知预测点,因此在利用分形插值进行预测时需要先确定下一个插值点(Pk+1,Qk+1)和纵向尺度因子dk+1.(Pk+1,Qk+1)可利用SVM算法求出,dk+1可根据(5)式求出.利用(Pk+1,Qk+1)和dk+1,再构建一个新的迭代函数系进行分形插值,得到相邻插值点(Pk,Qk)与(Pk+1,Qk+1)之间的所有数据{(Xi,Yi),i=m+1,m+2,…,m+l},且(Pk+1,Qk+1)=(Xm+l,Ym+l),l≤r.按此步骤继续下去,直至得到全部的预测数据{(Xi,Yi),i=m+1,m+2,…,m+r}. 选取上海证券综合指数(简称上证综指)2006年1月4日至2017年3月13日共2 718个日收盘数据作为R/S分析对象,以确认上证综指序列的分形特征和可预测性. 图1 上证综指的R/S分析结果Fig. 1 R/S Analysis Result of Shanghai Composite Index 图1是上证综指的R/S分析结果.由R/S分析可得H=0.680 4,从而可知上证综指的日收盘数据时间序列具有长程相关性,可用分形方法进行预测. 下面将上证综指2016年1月4日至2017年1月3日共245个日收盘数据作为分形插值研究对象,这些原始数据如图2所示.通过间隔为4的等距分割选取插值点,再利用(5)式计算纵向尺度因子,建立分形插值模型,对这245个日收盘数据进行插值拟合.图3给出了分形插值拟合的结果.从图3可以看出,采用纵向尺度因子的新计算方法所建立的分形插值模型对上证综指日收盘数据进行拟合,精度较高,表明该模型能很好地描述上证综指日收盘数据的走势. 图2 上证综指2016年1月4日至2017年1月3日的日收盘数据Fig. 2 Daily Closing Data of Shanghai Composite Index from 2016-1-4 to 2017-1-3 图3 上证综指2016年1月4日至2017年1月3日的分形插值拟合Fig. 3 Fractal Interpolation Fitting of Shanghai Composite Index from 2016-1-4 to 2017-1-3 接下来预测最后4天(2016年12月28—30日和2017年1月3日)的日收盘数据.根据分形插值法,要预测未来4天的数据,就需要知道下一个插值点(2017年1月3日)的日收盘数据和相应的纵向尺度因子.下面利用SVM算法来进行计算. 图4 SVM参数寻优结果Fig.4 Result of SVM Parameter Optimization 由于SVM模型预测的都是相邻的下一个点的值,因此需适当增加样本规模以提高预测精度.对1990年12月21日至2017年1月3日的上证综指日收盘数据每隔4天选取1个数据,就得到1 592个数据,以最后一个(2017年1月3日的收盘数据)作为预测数据.利用Matlab和LIBSVM进行参数寻优与建模,惩罚参数和核函数的取值范围均为[2-4,24].图4示出了SVM参数优化的结果. 通过SVM模型预测得到2017年1月3日的收盘数据为3 139.8元,再根据已知的di计算出插值区间2016年12月27日至2017年1月3日的参数d,这样就可以利用分形插值预测出2016年12月28—30日和2017年1月3日的日收盘数据.表1列出了原始数据与预测数据的比较结果. 表1 原始数据与预测数据的比较 图5 3种预测方法的比较Fig. 5 Comparison of Three Prediction Methods 提出了一种确定分形插值迭代函数系纵向尺度因子的新方法,并由此建立了一个改进的分形插值模型.将该模型与SVM模型相结合,构造了可以预测时间序列变化趋势的混合预测模型.将混合预测模型应用于上证综指日收盘数据的分析和预测:通过R/S分析得到上证综指日收盘数据的Hurst指数为0.680 4,说明上证综指的日收盘数据具有长程相关性,是可预测的;利用改进的分形插值模型对上证综指2016年1月4日至2017年1月3日的日收盘数据进行分形插值拟合,获得了很好的拟合效果;利用混合预测模型对上证综指2016年12月28—30日和2017年1月3日的日收盘数据进行预测,预测效果较另外2种方法更好.笔者相信,基于改进的分形插值与SVM的混合预测模型在对时间序列的分析和预测中将有广泛的应用. 参考文献: [1] MANDELBROT BENOIT B.New Methods in Statistical Economics[J].Journal of Political Economy,1963,71(5):421-440. [2] PETERS EDGAR E.Fractal Market Analysis:Applying Chaos Theory to Investment and Economics[M].New York,Chichester,Brisbane,Toronto,Singapore:John Wiley & Son,Inc.,1994. [3] 王明涛.基于R/S法分析中国股票市场的非线性特征[J].预测,2002,21(3):42-45. [4] YUAN Ying,ZHUANG Xintian,JIN Xiu.Measuring Multifractality of Stock Price Fluctuation Using Multifractal Detrended Fluctuation Analysis[J].Physica A:Statistical Mechanics and Its Applications,2009,388(11):2 189-2 197. [5] 王宏勇,郭丽娜.国际黄金期价与美元指数交互关系的多重分形分析[J].数理统计与管理,2015,34(5):878-889. [6] RICHARDS GORDON R.A Fractal Forecasting Model for Financial Time Series[J].Journal of Forecasting,2004,23(8):586-601. [7] NI Liping,NI Zhiwei,GAO Yazhuo.Stock Trend Prediction Based on Fractal Feature Selection and Support Vector Machine[J].Expert Systems with Applications:An International Journal,2011,38(5):5 569-5 576. [8] MOGHADDAM AMIN HEDAYATI,MOGHADDAM MOEIN HEDAYATI,ESFANDYARI MORTEZA.Stock Market Index Prediction Using Artificial Neural Network[J].Journal of Economics,Finance and Administrative Science,2016,21(41):89-93. [9] OZTEKIN ASIL,KIZILASLAN RECEP,FREUND STEVEN,et al.A Data Analytic Approach to Forecasting Daily Stock Returns in an Emerging Market[J].European Journal of Operational Research,2016,253(3):697-710. [10] BARNSLEY MICHAEL F.Fractal Functions and Interpolation[J].Constructive Approximation,1986,2(1):303-329. [11] WANG Hongyong,YU Jiashan.Fractal Interpolation Function with Variable Parameters and Their Analytical Properties[J].Journal of Approximation Theory,2013,175(4):1-18. [12] 王宏勇,马 丽.基于分形插值模型的股价时间序列分析及预测[J].统计与决策,2009(16):29-30. [13] ZHAI Mingyue.A New Method for Short-Term Load Forecasting Based on Fractal Interpretation and Wavelet Analysis[J].Electrical Power & Energy Systems,2015,69(1):241-245. [14] MAZEL DAVID S,HAYES MONSON H.Using Iterated Function Systems to Model Discrete Sequences[J].IEEE Transactions on Signal Processing,1992,40(7):1 724-1 734. [15] 梁 循.支持向量机算法及其金融应用[M].北京:知识产权出版社,2012:1-15. [16] TAY FRANCIS E H,CAO L J.Modified Support Vector Machines in Financial Time Series Forecasting[J].Neurocomputing,2002,48(1-4):847-861. [17] WANG Shuai,SHANG Wei.Forecasting Direction of China Security Index 300 Movement with Least Squares Support Vector Machine[J].Procedia Computer Science,2014,31:869-874. [18] WANG Jianzhou,HOU Ru,WANG Chen,et al.Improvedv-Support Vector Regression Model Based on Variable Selection and Brain Storm Optimization for Stock Price Forecasting[J].Applied Soft Computing,2016,49:164-178.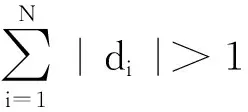
3 上海证券综合指数序列的分析与预测







4 结语

