船舶和海洋结构物建造中的计算焊接力学进展

王江超， 周 宏， 吴正峰， 杜仕忠， 鞠理杨， 刘建峰

(1.华中科技大学 船舶与海洋工程学院， 湖北 武汉 430074； 2.上海交通大学 高新船舶与深海开发装备协同创新中心，上海 200240；3．江苏科技大学 船舶与海洋工程学院， 江苏 镇江 212003； 4．南通振华重型装备制造有限公司，江苏 南通 226017；5．上海外高桥造船有限公司，上海 200137)

0 引 言

船舶及海洋结构物大多采用不同厚度的钢板进行建造，而焊接作为主要的金属连接方式被广泛应用。在焊接过程中和焊后，变形和应力作为基本的力学响应将不可避免地产生。焊接瞬态变形将严重影响焊接过程的顺利进行，而焊后变形则会影响焊接结构的制造精度。采用焊后矫正工艺会提高生产成本，并延长建造周期；焊接残余应力会严重影响焊接结构的力学性能以及使用寿命。

对于薄板焊接接头，由于热源基本贯穿厚度方向，故可描述为在厚度方向无应力的平面应力问题，对其进行分析求解。薄板焊接的突出困难在于焊接变形，尤其是面外变形。同时，中厚板(>20 mm)焊接接头多采用多层多道焊，其热循环过程复杂，热应力及残余应力交替变化，且厚板刚度大，不易产生焊接变形。因此，厚板焊接结构的主要问题是残余应力，将实际问题中的焊缝方向应变忽略，进而简化为平面应变问题也是合理的。

本文分析焊接接头力学响应的内在机理，进而优化焊接工艺和过程，对船舶和海洋结构物的焊接变形和残余应力进行预控研究，是当前先进制造技术和智能造船的重要内容。

1 研究方法和理论

针对船舶海洋结构物建造中的焊接变形和残余应力，需要用到计算焊接力学(Computational Welding Mechanics)的相关理论和方法。

1.1 热弹塑性有限元分析

焊接过程的热弹塑性有限元分析可以考虑2种物理现象：热传导和弹塑性力学[1]。由于热传导过程决定着后续的力学过程，非耦合的热-结构场分析可足够精确地分析焊接时的热力学行为。这种非耦合的热-结构分析使用线性热膨胀系数和其他热物理力学参数来考虑瞬态温度场对焊接应力、变形的贡献。具体分析过程分为2步：(1)使用热传递(热传导、对流和辐射)理论分析计算瞬态温度场；(2)将计算得到的瞬态温度场作为热载荷施加到随后的结构分析中，进行焊接残余应力、塑性应变和位移的计算。

1.2 固有应变理论

根据大量试验观察以及热弹塑性有限元计算分析[2]可知：焊接过程中的剩余压缩塑性应变是产生焊接变形的根本原因。焊缝在加热时会伸长，由于周围母材的约束，当压缩内应力大于屈服应力时，产生压缩塑性应变。冷却过程正好相反，焊缝在拉伸内应力的作用下可能产生拉伸塑性应变。这样在加热过程中产生的部分压缩塑性应变将被冷却过程中产生的拉伸塑性应变抵消，而剩余的压缩塑性应变则被保留下来，产生焊接变形。这些剩余的压缩塑性应变又称为固有应变。之所以称为固有应变，是由于其数值主要取决于焊接接头类型、材料性能、板厚以及焊接热输入等参数，而焊接接头的长度以及宽度(足够宽)影响可忽略不计。这样就可对小型的典型焊接接头进行试验测量和热弹塑性有限元分析，获得该焊缝的固有应变，然后将其加载到长焊缝上，通过弹性分析来预测大型结构的焊接变形。

综上所述，焊接加热冷却过程中的全应变可分为如式(1)所示的几个分量：弹性应变εel、热应变εth、塑性应变εpl、蠕变应变εcr和相变产生的应变εph。总应变也可考虑为弹性应变和固有应变的和。换言之，固有应变是除弹性应变之外的其他应变分量总和，即固有应变是热应变、塑性应变、蠕变应变和相变产生的应变的总和。固有应变可简单地使用塑性应变来表示，因为焊接过程中蠕变应变和材料固态相变引起的应变一般较小，可忽略不计；热应变会随着焊接结构温度降低到初始温度或室温而消失。因此，塑性应变是组成固有应变的各个应变中的最主要部分，并且可以通过试验测量或者热弹塑性有限元分析得到。

εtotal=εel+εth+εpl+εcr+εph

(1)

1.3 固有变形理论

受到加热温度和母材约束的影响，固有应变在距离焊缝的不同位置有着不同的值。想要通过直接加载固有应变进行弹性有限元分析来预测大型复杂船体结构的焊接变形，在实际应用中仍存在一定的困难。将垂直于焊缝横断面上的各固有应变分量进行积分，可得到对应分量的固有变形，如式(2)所示。对于足够长的焊缝，在忽略焊缝端部效应后，每个焊缝的力学特征可由4个固有变形分量来表达。

式中：x、y、z为焊缝方向、垂直焊缝方向以及厚度方向；h为板材厚度。

更进一步，焊缝在纵向(焊缝方向)和横向受到母材完全不同的自拘束作用。由于纵向的强拘束，纵向固有变形往往被转化为固有纵向收缩力，仅在焊缝及其附近产生收缩变形；在横向，焊缝均匀收缩，往往直接使用固有横向收缩来表征其焊接变形；角变形或者横向弯曲变形也因横向的自身弱拘束，可直接由面外弯曲弧度来替代；纵向弯曲因其数值过小，经常被忽略而不予考虑。

2 轻量化造船中的薄板结构焊接失稳

船舶和海洋结构物的焊接占据建造过程近一半的工时和工作量，而焊接结构的基本单元是各种船体典型焊道、简单加强筋结构以及各功能分段。依次对其焊后产生的焊接失稳变形进行分析：焊接失稳变形的分布和数值，焊接失稳的临界条件和对应的模态。

2.1 薄板焊接接头的失稳分析

典型的对接焊或者T型角焊，在焊缝收缩的作用下失去稳定性，会表现出多种与初始装配状态完全不同的结构形态，且焊接失稳变形没有简明的变形形式，很难判断。

在简单的薄板堆焊以及对接焊接头中，焊接失稳变形呈现出“马鞍形”的模态，如图1焊接试件(长度为300 mm，宽度为200 mm，厚度为2.28 mm的低碳钢薄板)所示。根据固有变形方法和大变形理论，弹性有限元分析的计算结果不仅给出相同的失稳变形模态，其预测数值也与试验测量具有较好的一致性；对该焊接接头作特征值分析，可求出在焊接作用下失稳发生的最低模态和对应的临界条件(马鞍形：27.50 kN)。

图1 船舶机舱及设备建模流程图

对于T型角焊接头，焊接失稳变形可能以多种形式呈现， 如图2给出的常见的失稳变形形式。基于特征值分析：底板长为500 mm，宽为400 mm，立板高为200 mm且厚度都为2 mm的船用钢T型焊接接头，可能产生的低阶的失稳模态是整体的扭转变形。

图2 T型角焊接头的失稳变形

针对典型的焊接接头(对接焊和角接焊)，弹性有限元分析和特征值分析都得出如下的结论：焊接失稳变形仅由固有纵向收缩力来决定；固有横向弯曲(角变形)和固有纵向弯曲(通常因数值相对较小而忽略不予考虑)，都不会决定焊接失稳变形是否发生；但它们与初始扰度一起作为外部扰动，在失稳条件满足时，会促发焊接失稳现象的发生；固有横向位移在此对焊接失稳没有任何影响。当然，在没有任何扰动的情况下，即使焊接产生的纵向收缩力大于产生失稳的压缩力，焊接失稳也不会发生。

2.2 薄板加强筋结构的失稳分析

针对高强钢薄板稳定性不佳的特点，船体结构一般采用加强筋结构来提高其刚度，保证其服役期间的力学性能。然而，对于常见的加强筋焊接结构，依然可能产生焊接失稳变形。

图3a)给出了1块正方形纵横交错的加强筋焊接结构，其中，底板为1 200 mm×1 200 mm×6 mm的正方形钢板，较低和较高的加强筋高度分别为100 mm和150 mm，且厚度都为9 mm。经过半自动手工电弧焊完成各加强筋和底板的焊接之后，得到了中部凸起、各边稍微凹陷的面外变形分布。根据固有变形和界面要素的弹性有限元方法，不但给出了失稳模态相同的焊接面外变形分布，其预测数值也具有较好的一致性。针对该加强筋结构和当前的焊接工艺，使用特征值分析来计算可能产生的低阶焊接失稳模态，可得到如图3b)所示的结果。

图3 标准纵横垂直的加强筋结构

然而，对于图4a)所示的加强筋结构，在焊接作用下产生的失稳变形却迥然不同。该加强筋结构由底板(1 200 mm×600 mm×6 mm)、2块纵向加强筋(1 000 mm×100 mm×6 mm)以及3块横向加强筋(500 mm×100 mm×6 mm)等构成。焊接结束后，加强筋产生整体扭转的大变形，其变形值高达105 mm，此为扭转失稳变形。弹性有限元同样给出结构整体扭转的焊接失稳变形模态，且预测的最大变形量与试验测量极其吻合。应用特征值分析来计算该特殊加强筋结构在当前焊接工艺作用下可能产生的低阶焊接失稳模态，可得到如图4b)所示的结果。

图4 纵横垂直的加强筋结构失稳变形

理论及计算分析表明：在相互垂直的加强筋焊接结构中，横向位移在垂向加强筋的约束下，不能随意移动时，面内固有收缩(纵向收缩力和横向位移)共同决定焊接结构是否发生失稳现象；焊接产生的面外横向/纵向弯曲以及初始扰度，依然只会在结构满足失稳条件时，促使结构失去稳定性，产生失稳变形。

2.3 船体板架结构的失稳分析

船体板架结构是船体结构最常见的构建形式，在其焊接制造过程中，焊缝处产生的固有变形会使得该结构产生一定的面外变形。焊接产生的面外变形主要由面外弯曲角变形和失稳变形共同决定。在中厚板及厚板结构中，由于失稳变形没有发生，面外变形仅由面外弯曲角变形引起，底板会呈现出“瘦马”形态的面外变形。失稳变形产生后，如图5所示，焊接结构表现出来的特征有：(1)底板多处产生凹凸不平的波浪式变形；(2)底板面外产生很大量级的变形。

图5 薄板船体板架结构焊后的面外(失稳)变形分布

然而，当焊接产生的面外弯曲角变形太大时，其对面外变形的贡献会掩盖焊接失稳现象，使得焊接失稳的特征表现得不够明显。当然，面外变形也受到焊缝收缩力产生的弯曲力矩的影响。当焊接结构横断面的质心位置与其受力点的位置(焊缝)不相同时，就会产生一定的弯曲力矩，也可能使焊接结构产生面外变形。

综上所述，焊接失稳变形是一个现象复杂且呈现多变模态的变形类型，特别是在大型且复杂的焊接结构中，其表现形式变得异常多样化，而相关的机理分析和计算分析预测都非常困难。

3 海洋平台大厚板焊接残余应力预测

厚板结构的焊接力学响应主要体现在焊接残余应力的分布，以及其对焊接接头和焊接结构强度、断裂、疲劳等的影响。基于热弹塑性有限元分析，在得到焊接变形的同时，也能得到焊接残余应力在不同方向上的分布及数值。本节主要对南通振华重型装备制造有限公司设计建造的自升式钻井平台的悬臂梁结构进行焊接残余应力的计算，并给出当前存在的问题及相关研究进展。

3.1 对接及角焊接头残余应力计算

对于厚度为76 mm的厚板结构，其焊接接头的相关工艺参数和焊道布置如表1所示。对应的有限元模型，采用Solid实体单元，如图6所示(单元：45 750；节点：49 352)。同时，计算所得的焊接残余应力如图7所示。

表1 76 mm厚板对接焊工艺及焊道布置

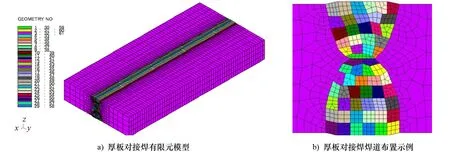
图6 76 mm厚板对接焊有限元模型

图7 76 mm厚板对接焊残余应力分布

T型焊接接头也是自升式平台中悬臂梁结构的重要连接形式，对于底板厚度为76 mm、立板厚度为44 mm的T型结构，其焊接接头的相关工艺参数和焊道布置如表2所示。对应的有限元模型采用Solid单元，如图8所示(单元：33 672；节点：36 952)。同时，计算所得的焊接残余应力如图9所示。

表2 T型焊接接头(76 mm+44 mm)工艺及焊道布置

图8 T型焊接接头(76 mm+44 mm)有限元模型

图9 T型焊接接头(76 mm+44 mm)残余应力分布

3.2 厚板焊接残余应力分析的不足及展望

虽然热弹塑性有限元分析可用来预测和研究厚板多层多道焊的焊接残余应力，但还存在许多问题须解决，可归纳如下。

3.2.1 计算机资源及计算时间的消耗

厚板焊接接头的典型特点就是多层多道焊，这使得有限元模型的节点数和单元数往往有数十万之多，其有限元分析对计算机资源的需求特别大，而且计算的时间也特别长，如图10所示。当前，计算焊接力学在求解方程时，常用迭代法和直接消元法。为克服上述问题，在软件及程序方面，常将大规模的非线性问题转化为1个小规模的非线性问题和1个大规模的线性问题进行求解[3]；而在硬件方面，使用并行计算将求解域分割成几个子域同时求解，或者使用GPU替代CPU做数值计算[4]。

3.2.2 多层多道焊的热处理及固态相变

低碳钢以及合金钢在焊接的热循环过程中都会发生微观组织的固态相变：在升温过程中得到奥氏体，而在冷却过程中，会因冷却速率的不同得到铁素体、贝氏体以及马氏体，如图10a)所示[5]。同时，由于各种金属相的体积不同，会产生一定的膨胀和收缩，即相变应变(TRIP)[6]。这将导致产生新的内应力，影响最终的焊接残余应力，如图10b)所示。

3.2.3 多层多道焊的塑性应变强化

材料在拉伸作用下会产生内应力。当内应力大于材料的屈服极限时，则发生屈服，产生塑性应变及变形。当外力卸载之后再次加载时，材料的屈服极限会发生变化，有增强的现象，称之为塑性加工硬化。常见的理论有：随动强化理论和等效强化理论。然而，在焊接过程中，动态强化准则[7]认为：内应力及塑性应变，不但受到位移变化的影响，还受到温度变化的影响，如图11所示。

图10 焊接过程中的金属相变

图11 数值计算的等效塑性应变

4 焊接接头强度及力学性能评估

焊接接头强度是指焊接接头承受外部载荷的能力，包括焊接接头的基本强度以及抗断裂和抗疲劳性能等。焊接的根本目的就是要使金属材料达到分子间的结合，进而使构件之间形成足够强度的连接。焊接接头的强度受到各种因素的影响，总的可归纳为如下几个方面。

(1) 几何不规则性。几何不规则性是指平直且表面光滑的板材，焊前开坡口，且在焊接过程使用引熄弧板以及垫板，并在焊后形成余高、焊瘤、烧穿、弧坑与咬边时产生的接头横截面突变和焊缝外形不平整，以及其引起的应力集中现象。

(2) 材质不连续性。焊缝的横截面上出现的气孔、未焊透以及初始裂纹都是焊接接头材质不连续的现象。在这些地方，焊接接头的力学性能受到很大的影响，而且这些缺陷的扩展会造成材质不连续性的加剧，使得焊接接头迅速失效。

(3) 组织性能不均匀性。有时候，焊接没有几何或者连续性方面的缺陷，但是其组织性能不均匀，例如：未熔合、夹渣、残余内应力腐蚀、固态相变、晶粒尺寸以及焊缝熔合线两侧等，也将严重影响焊接接头的使用性能。

上述的焊接加工缺陷，对焊接接头和焊接结构的力学性能评估有着非常重要的影响。因此，在数值模拟中，须假设一定的缺陷模型进行分析。

5 结 论

船舶和海洋结构物的建造过程离不开焊接，而焊接不可避免地产生变形和应力2种力学响应。本文分析轻量化造船中薄板结构焊接失稳变形、海洋平台厚板接头的焊接残余应力，以及焊接加工缺陷的分类，总结当前船舶海洋结构物焊接数值模拟中存在的问题以及取得的一些进展。

[][]

[1] WANG J C, SHERIF R, HIDEKAZU M，et al. Investigation of Buckling Deformation of Thin Plate Welded Structures [C]//Proceedings of the 21th International Offshore and Polar Engineering Conference, 2011.

[2] 上田幸雄, 村川英一, 麻宁绪(著).焊接变形和残余应力的数值计算方法与程序[M]. 罗宇, 王江超,译.成都：四川大学出版社, 2009.

[3] HIROYASU N, HISASHI S，HIDEKAZU M. Actual application of FEM to analysis of large scale mechanical problems in welding [J]. Science & Technology of Welding & Joining, 2007,12(2): 147-152.

[4] MASAKAZU S, KAZUKI I, SHINSUKE I，et al. Computational method for transient welding deformation and stress for large scale structure based on dynamic explicit FEM [J]. Quarterly Journal of the Japan Welding Society, 2011, 29(1): 1-9.

[5] PARAMJEET K. Coupling microstructure to heat transfer computation in weld analysis [D].Ottawa:Carleton University, 1989.

[6] DEAN D. FEM prediction of welding residual stress and distortion in carbon steel considering phase transformation effects [J]. Materials and Design, 2009(30)：359-366.

[7] QIAO D X, FENG Z L, ZHANG W, et al. Modelling of weld residual plastic strain and stress in dissimilar butt weld in nuclear reactors [C]//Proceedings of the ASME Pressure Vessels and Piping Conference, 2013.