空间站对日定向装置试验台的控制器设计与精度考核

贺 云，张飞龙，刘明洋，徐志刚 (. 中国科学院沈阳自动化研究所，沈阳 006；2. 中国科学院大学，北京 00049)

0 引 言

2016年11月28日鑫诺卫星通信公司正式宣布：我国第一代通信广播卫星“鑫诺二号”发生技术故障，太阳能帆板展开失败，导致20亿人民币的损失。太阳帆板打开和姿态调整是飞船或卫星发射的最后一步工序，能否完成标志着整个发射的成败。但是国内外在关于太阳帆板驱动装置的驱动性能考核方面的技术文献很少公开。因此本文设计了一套空间站对日定向装置试验台，来考核空间站对日定向装置对太阳能电池帆板的驱动性能。

空间站在轨运行的主要能量源于太阳电池帆板吸收的太阳能，对日定向装置用于驱动太阳电池帆板的转动，将其调整到太阳能利用率最高的角度。由于太阳电池帆板具有大挠性、大惯量等特性，造成对日定向装置的驱动过程面临大力矩、高频响的变负载作用。因此对日定向装置在出厂之前或研制过程中，需要检测它在太空运行状态下对太阳电池帆板的驱动性能[1]。

中国空间技术研究院[2-4]、哈工大[5]和上海交大[6-7]等单位采用实际卫星太阳电池帆板或帆板产品模型[8]对所设计的帆板驱动装置的驱动性能进行地面试验考核，取得了较为理想的结果，但其模型没有排除重力的影响，不适用于大挠性的空间站太阳帆板的地面试验[9]。

沈阳自动化研究所采用气浮补偿卫星电池帆板的重力，对驱动装置的驱动性能进行地面试验考察，但仅适用于小尺寸、刚度较大的太阳帆板驱动装置的性能考察[10]。

空间站太阳电池帆板的尺寸比卫星太阳电池帆板的尺寸和柔性更大，采用气浮的方法会由于重力的作用出现翻折现象，难以使其竖直站立；采用吊挂[11-14]进行重力补偿的地面仿真实验面临着较大的阻力[15]以及由于柔性过大导致的重心难以跟随的问题；采用缩尺模型会改变实验对象原有的机械特性[16]。因此实际空间站太阳电池帆板不具备做地面物理仿真实验的条件。

本文设计了一套空间站对日定向装置试验台，用于模拟对日定向装置对太阳电池帆板驱动过程中，由不同状态下太阳电池帆板对对日定向装置施加的负载力矩。该试验台如图1所示，其原理图如图2所示，主体结构固定在大地上，对日定向装置下端通过扰动扭矩传感器与试验台主体结构连接，上端与加载单元通过法兰连接。采用电动负载模拟器作为加载单元，圆光栅测量的对日定向装置输出端的转角作为柔性太阳电池帆板动力学模型(加载单元)的输入，可计算出太阳电池帆板作用于对日定向装置的负载力矩，由加载单元对其施加等效负载力矩，为对日定向装置驱动性能的考核模拟出期望的太阳电池帆板负载力矩。

图1 空间站对日定向装置半物理仿真试验台Fig.1 The space station sun-tracking unit semi-physical simulation test device

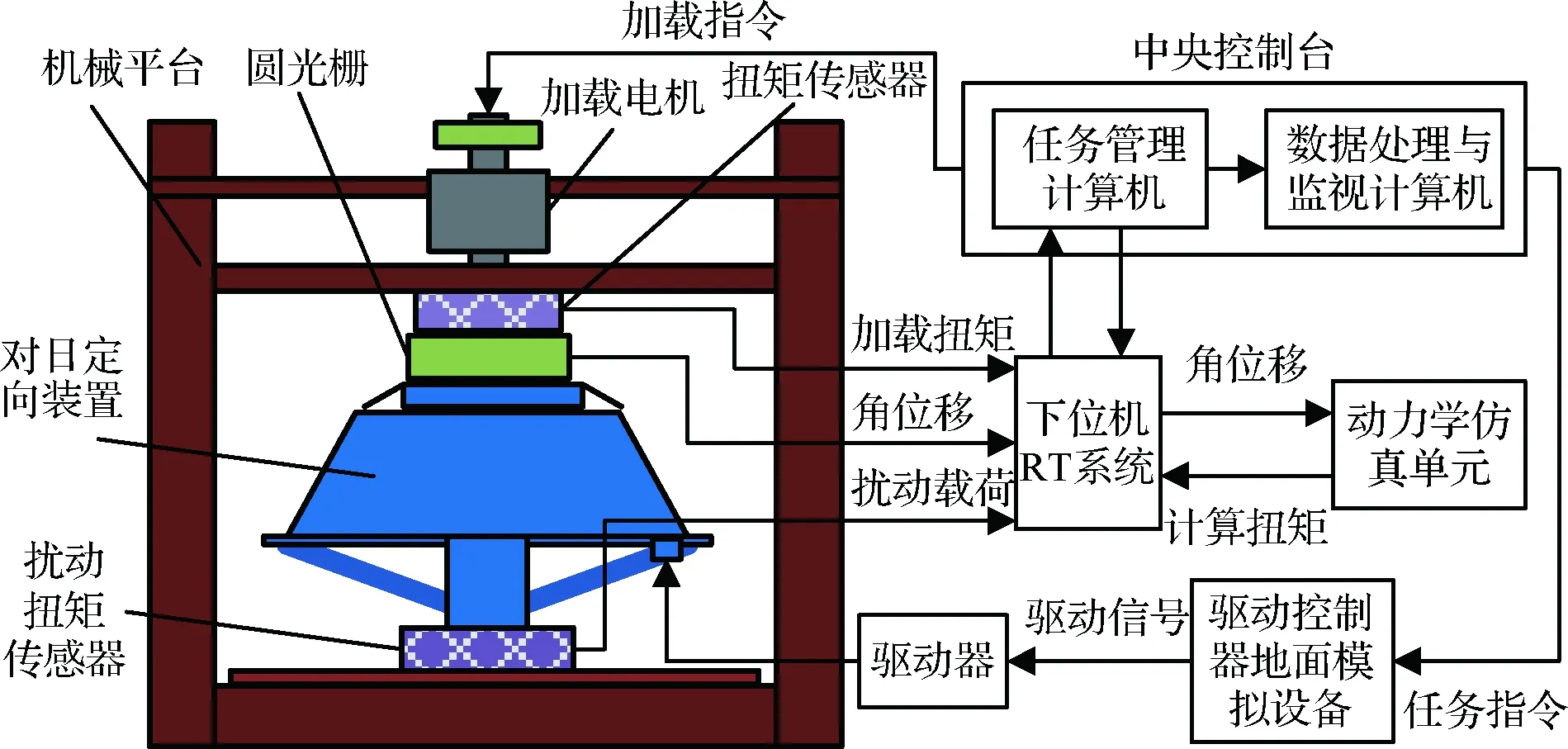
图2 空间站对日定向装置半物理仿真试验台原理图Fig.2 Principle diagram of the space station sun-tracking unit semi-physical simulation test system

本文根据对日定向装置低速大力矩高精度加载特点进行研究，建立试验台加载单元数学模型并对其各参数进行辨识，通过对模型各参数的调整，分析各个环节对系统性能的影响规律，然后设计出效果良好的复合控制器，使加载力矩较好的复现了太阳电池帆板模型的期望输出力矩，为对日定向装置对太阳电池帆板的驱动性能考核模拟出较为精确的期望负载(加载)力矩，完成了对日定向装置驱动性能的地面考核。

1 系统建模分析

加载单元用于模拟太阳电池帆板对对日定向装置的加载力矩，通过连接机构被动跟随对日定向装置运动，与对日定向装置的运动规律保持一致。对日定向装置驱动太阳电池帆板模型转动时，为实现加载单元对对日定向装置施加高精度的测试力矩，不仅对执行机构、测量装置的精度和性能有较高的要求，而且对于控制策略选择也至关重要，前提是建立精确的数学模型，本文以永磁同步电机(加载单元)直接驱动的电动负载模拟器为研究对象，建立加载单元对对日定向装置加载的试验台的控制系统模型如图3所示。

图3 试验台的控制系统框图Fig.3 Diagram of control system of test device

KPWM为PWM驱动环节放大系数，TPWM为PWM驱动环节延时周期，Tm为加载力矩指令，KT为电机转矩系数，Ke为反电势系数，Lm为电机线电感，Rm为驱动电机线电阻，Jm为转子转动惯量，Bm为摩擦阻力系数，KA为连接刚度。

由于太阳电池帆板具有大挠性、大惯量等特性，实际运行情况下对日定向装置工作在低速模式，此时可忽略反电动势的影响。如图4所示驱动器内置电流环为PI环节，可将电机的电流环模型用典型二阶环节近似。

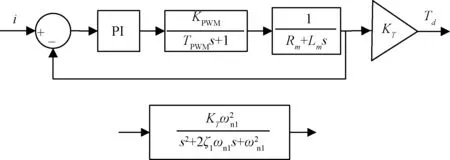
图4 加载单元简化结构框图Fig.4 Simplified block diagram of the loading unit

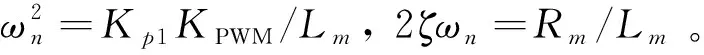
采用递推最小二乘法对加载单元模型进行辨识。对于自回归各态历经(ARX)模型：

A(z-1)y(k)=B(z-1)u(k-d)+ξ(k)

(1)

其中ξ(k)为系统噪声，

A(z-1)=1+a1z-1+a2z-2+…+anaz-na

(2)

B(z-1)=1+b1z-1+b2z-2+…+bnaz-na

(3)

将上述离散时间参数模型，转换为最小二乘形式：

y(k)=-a1y(k-1)-…-anay(k-na)+

b1u(k-d)+…+bnbu(k-d-nb)+ξ(k)

=φT(k)θ+ξ(k)

(4)

φ(k)= [-y(k-1),…,-y(k-na),

u(k-d),…,bnbu(k-d-nb)]T

(5)

θ=[a1,…,ana,b1…,bnb]T

(6)

带有遗忘因子的递推最小二乘法估计公式：

(7)

(8)

(9)

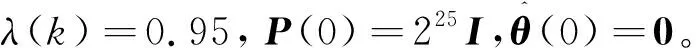
将上述辨识得到的ARX模型转化为传递函数模型，用于后续控制器设计。另外通过不同的方法得到的传递函数基本一致，进一步验证了所辨识模型的可靠性，传递函数为：

(10)

图5所示分别为加载单元模型的阶跃响应实测曲线与辨识曲线。

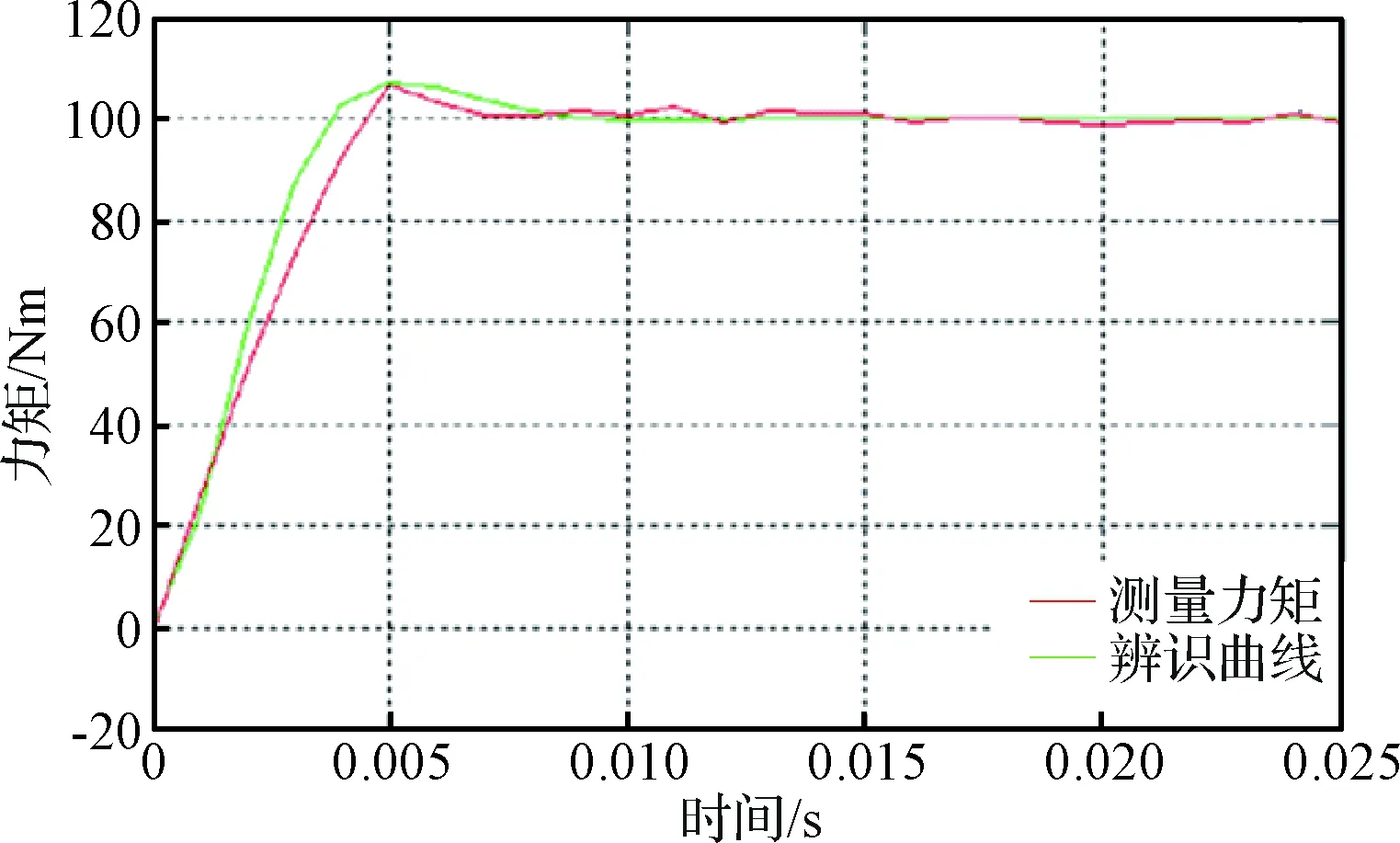
图5 加载单元模型跃响应实测与辨识曲线对比Fig.5 Comparison between measured and identified curves of step response of loading unit model

根据所求的加载单元传递函数，控制系统模型可以简化为由PID环节、加载单元模型和对日定向装置模型三部分构成的传递函数，如图6所示。

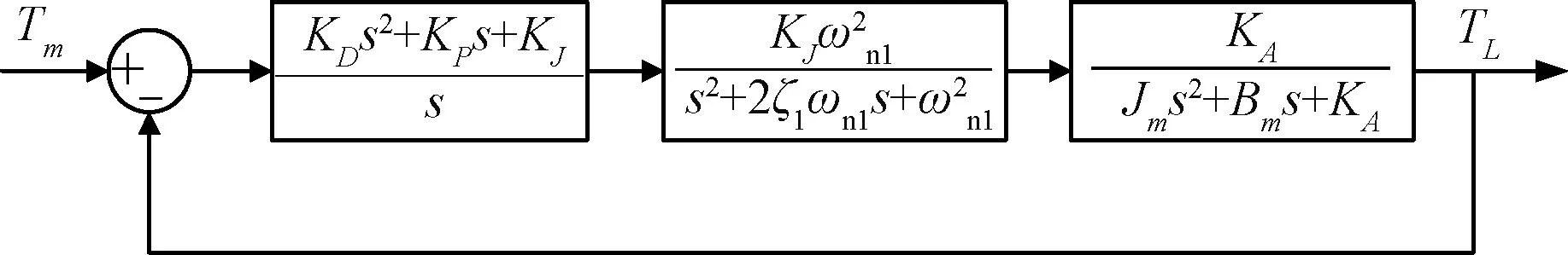
图6 控制系统简化框图Fig.6 Simplified block diagram of loading system

(11)

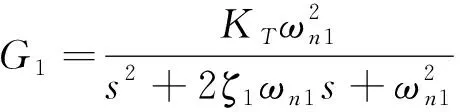
(12)

(13)

控制系统开环传递函数，

(14)

式(14)中需要进一步辨识的参数包括对日定向装置的转动惯量Jm，摩擦阻力系数Bm和连接刚度KA。

(1)连接刚度

图7 刚度测试系统Fig.7 Stiffness test system

如图7所示，O点和A点分别装有圆光栅，B点为安装夹具，可视B点以下的刚度为无穷大。C点装有扭矩传感器。

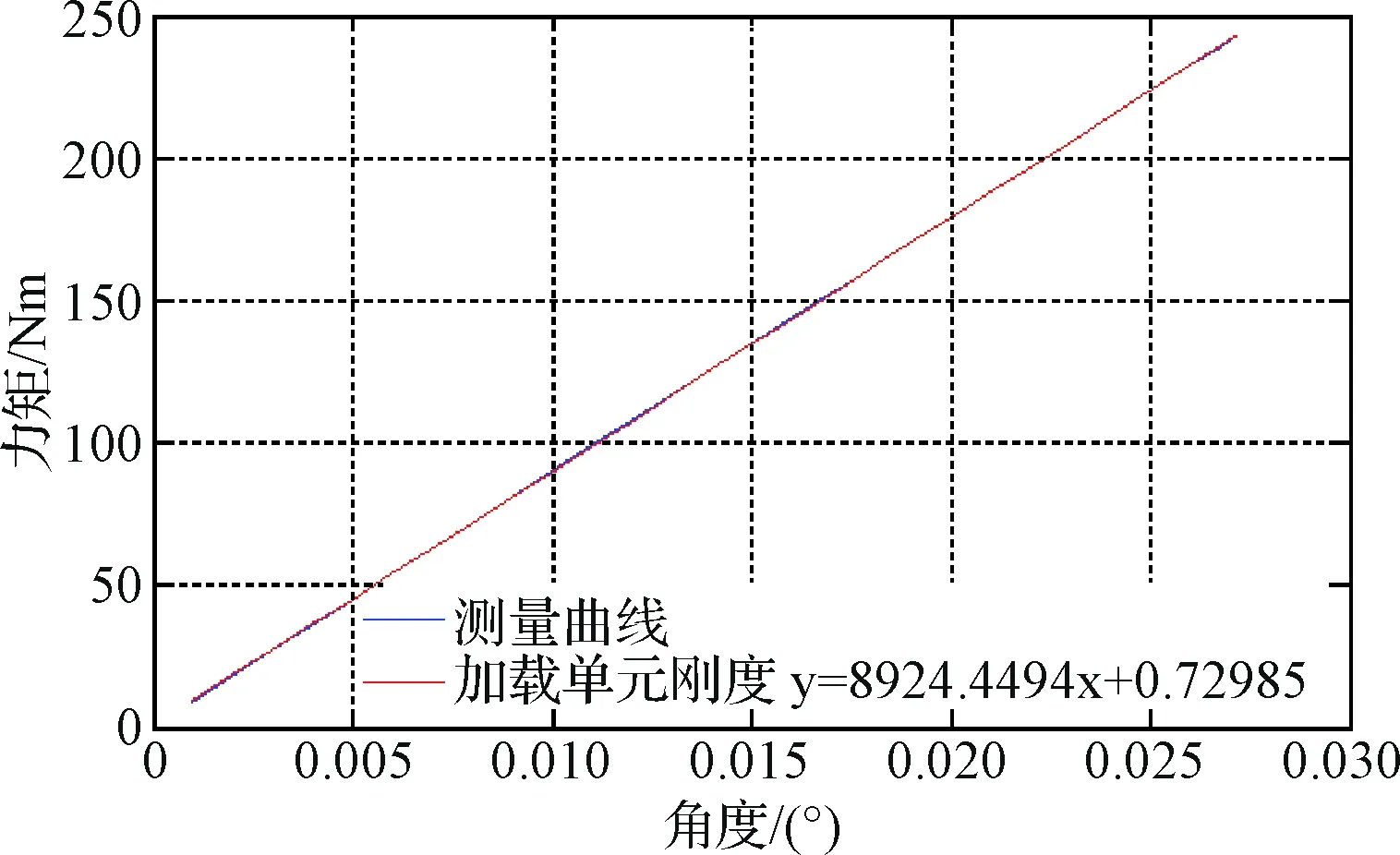
图8 加载单元刚度测试图Fig.8 Figure of stiffness of electrical servo load simulator

由加载单元输出0～240 Nm的加载力矩，记录O点处的转角θ1、A点处的转角θ2和C点处的扭矩传感器测量值T。根据图8采用最小二乘法可求得输出轴的连接刚度KA：

T=ka(θ1-θ2)+bl

(15)

(2)惯量和阻尼

系统惯量和阻尼均采用在标称值上微修正的方法处理，如图9所示的对日定向装置的响应曲线，对日定向装置模型可近似为典型二阶系统，且整个控制系统的主导极点近似为对日定向装置的极点。求得该系统开环传递函数为：

(16)

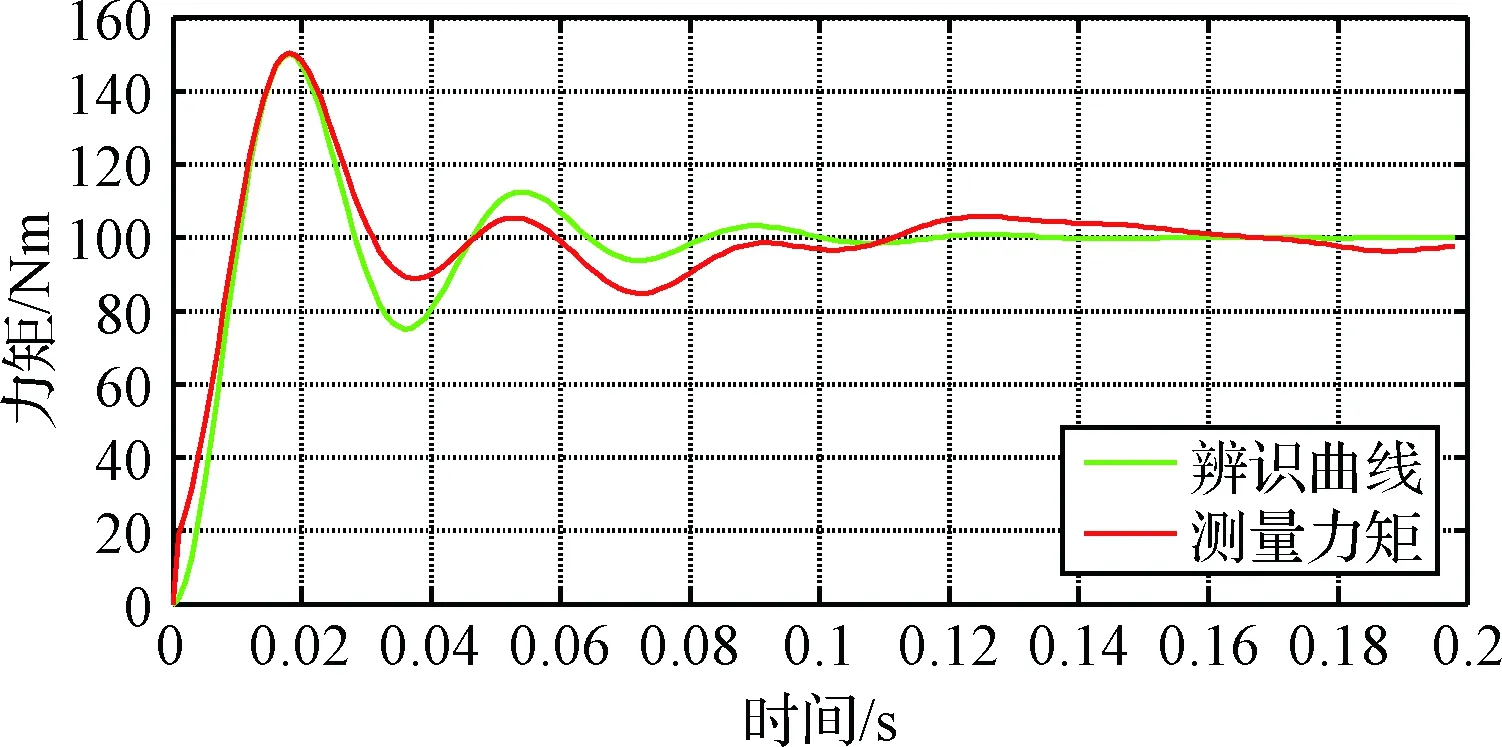
图9 实测与辨识曲线对比Fig.9 Comparison between measured curves and identified curves

2 控制器设计

2.1 超前校正

加载单元主要针对频率为0～10 Hz的工作频段，从图11的bode图可以看出，在工作频段的输出呈现出较大的延时和衰减的特性，且在中高频段有较大的相角滞后，为提高系统的跟随性能，本文在控制系统的前向通道上串联超前校正环节，以增大前向通路的相位，减小滞后，同时选择合适的参数，抵消惯性环节对工作频段幅频响应的衰减作用，将工作频段的对数幅频曲线保持在0 dB附近，从而增大带宽，加载单元补偿后的结构框图如图10所示。

设超前环节的传递函数为：

(17)

其中，a为滞后超前比(a>1 ) ，T为超前校正时间常数。通过调节a和T，使得零、极点在负实轴上移动，保证工作频段位于1/aT和1/T之间，呈现出微分作用，串联校正后控制系统的Bode图如图11所示。

根据图11，对比校正前后的bode图可看出，校正环节为控制系统提供了附加相位，较好地补偿了工作频段的滞后，0～5 Hz几乎没有滞后，5～10 Hz滞后开始出现，并呈现缓慢增大趋势，滞后最大值发生在10 Hz高频处为20 °；同时，该校正装置抵消了工作频段的惯性环节，将-20 dB/dec的斜率提到了0 dB/dec，保证了控制系统的对数传递函数在工作频段之间保持在0 dB处，较好地跟踪系统输入信号的幅值特性。

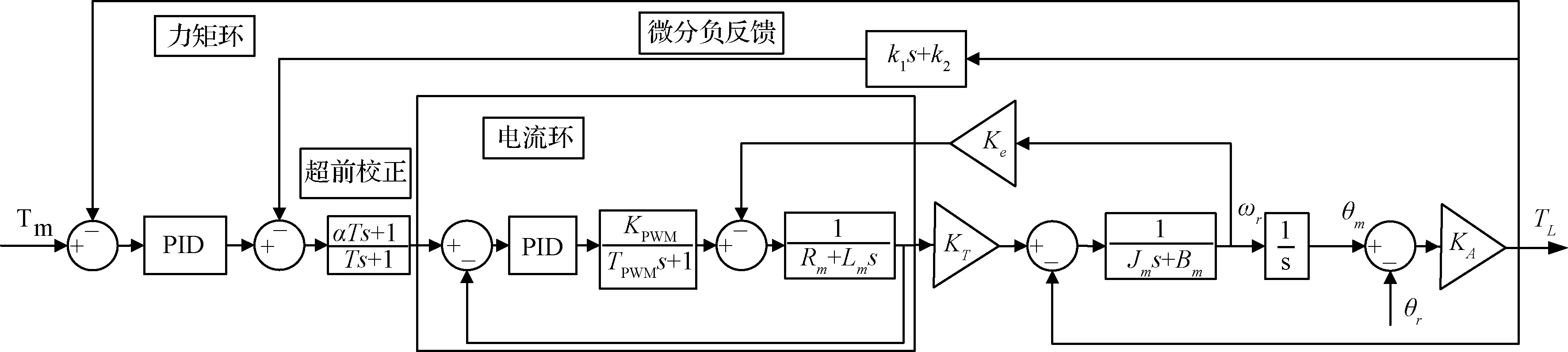
图10 加载单元补偿结构框图Fig.10 Diagram of electrical servo load simulator after corrected

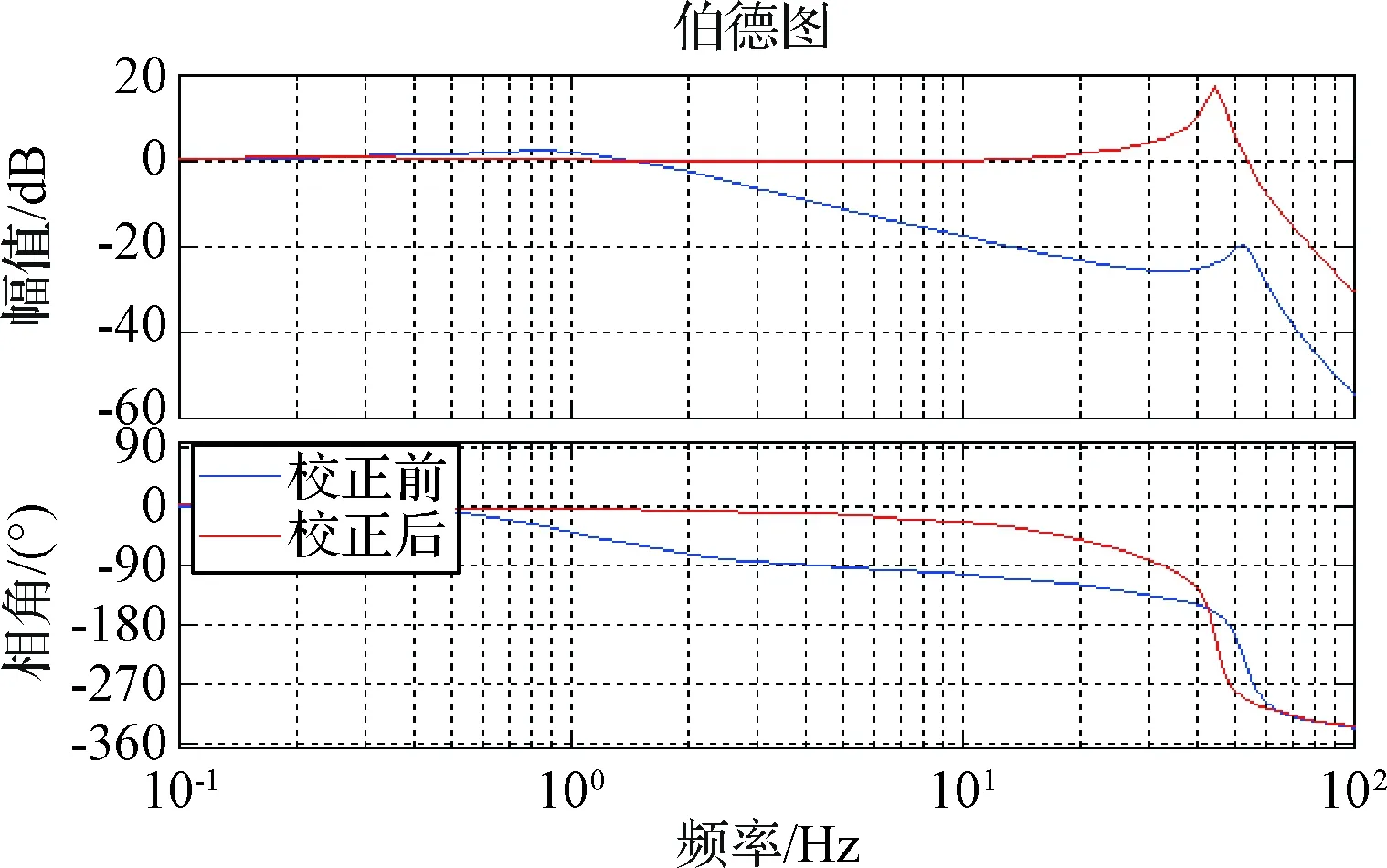
图11 校正前后的bode图Fig.11 Bode diagram before and after calibration

2.2 模糊自适应PID控制

该测试系统具有非线性和不确定的时变特点，如存在负载(对日定向装置)和系统参数变化等问题，由于经典PID控制的参数KP、KI、KD都固定，即使合理调节、整定这三个参数，也很难保证加载单元(永磁同步电机)对对日定向装置的加载力矩获得良好的控制性能。本文采用模糊自适应控制，对控制器PID参数KP、KI、KD实时调整，来改善加载单元对对日定向装置的力矩加载精度和快速性。

在常规PID控制器的基础上，以误差和误差变化率作为输入。将偏差e和偏差变化率ec作为模糊控制器的输入，PID控制器的三个参数ΔKP、ΔKI、ΔKD作为输出。根据工程实际情况，输人变量e和ec的模糊子集为{负大、负中、负小、零、正小、正中、正大}，记为{NB,NM,NS,ZO,PS,PM,PB}，将偏差e和偏差变化率ec量化到(-3, 3)的区域内。同时，输出变量ΔKP、ΔKI、ΔKD的模糊子集{负大、负中、负小,零、正小、正中、正大}，记为{NB, NM, NS, ZO, PS, PM, PB}，分别将其量化到(-0.3, 0.3) (-0.06, 0.06) (-3, 3)的区域内。

根据各模糊子集的隶属度赋值表和各参数的模糊控制模型，应用模糊合成推理设计PID参数的模糊矩阵表，在线修正PID参数，计算公式如下：

(18)

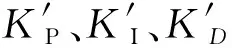
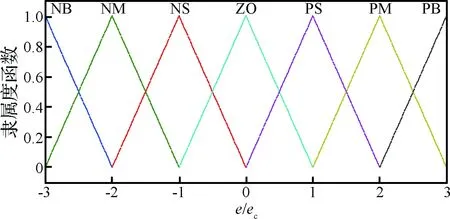
图12 输入变量e/ec的隶属函数Fig.12 Membership function for error e/ec

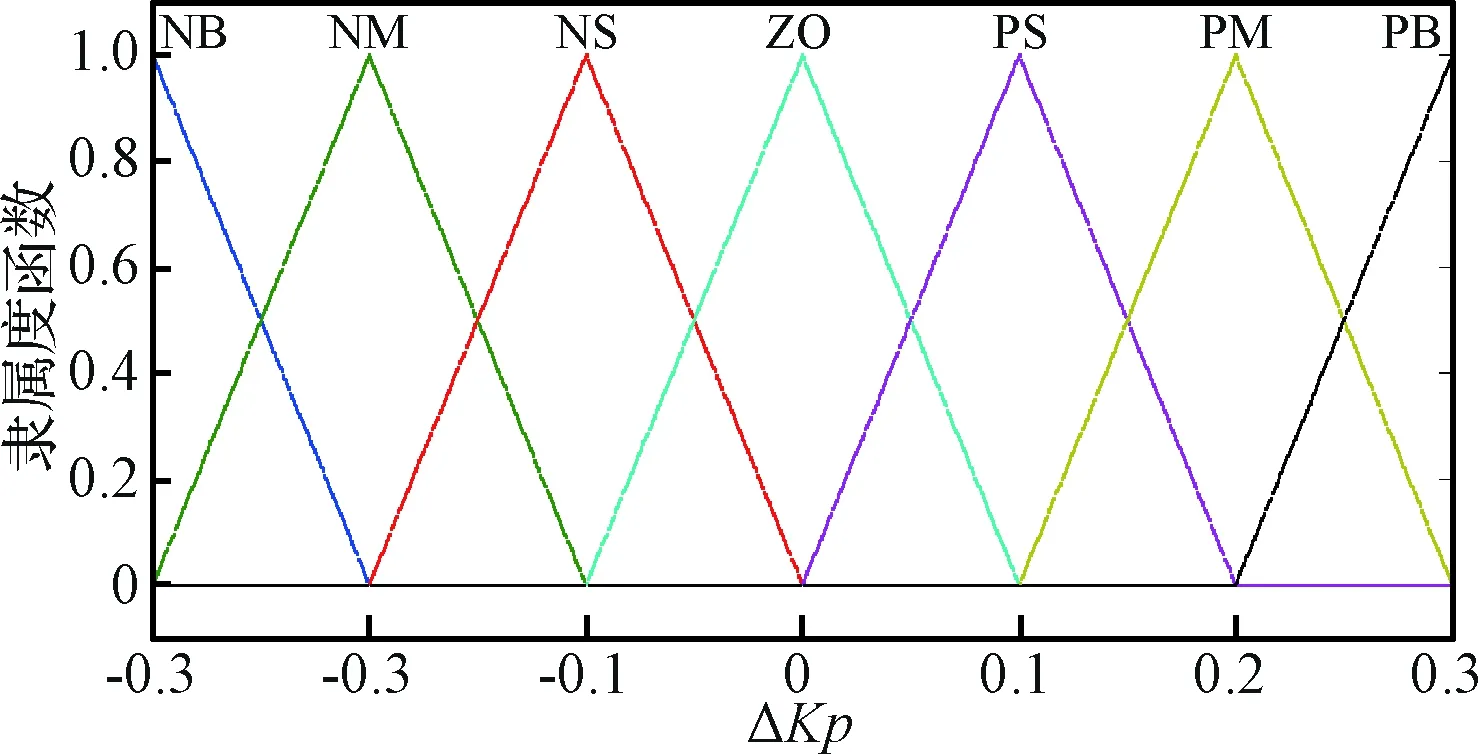
图13 输出变量 ΔKP的隶属函数Fig.13 Membership function for ΔKP

同理，得出输出量ΔKI、ΔKD的输入输出的隶属函数。根据模糊控制规则和隶属函数，采用Mamdani推理方法，以误差和误差变化为输入，则第ij条模糊控制规则表达形式为

Ruleij：若e=μi和ec=μj则u=uij

根据以往的工程经验，列写模糊自适应整定PID控制规则如表1所示：

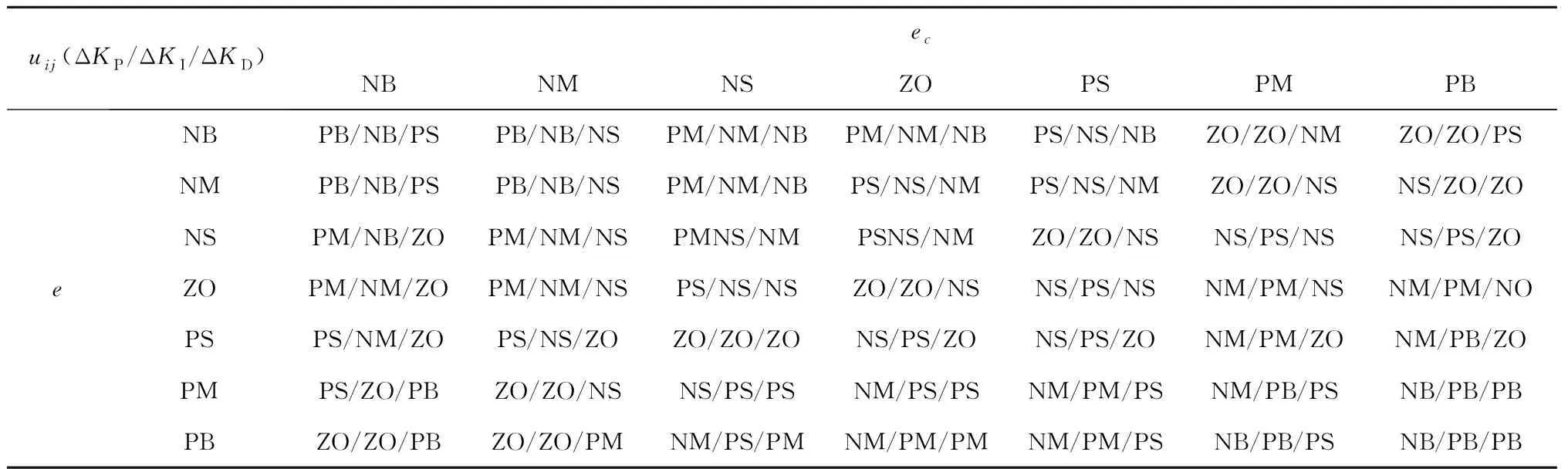
表1 模糊规则表Table 1 Fuzzy rule table

根据上面的模糊规则，对于输入偏差e和偏差变化ec经过推理可以得出相应的输出。

首先求出输出变量的隶属度，对应于ΔKP的第ij条模糊规则的隶属度为:

μij(ΔKP)=min{μi(e),μj(ec)}

(19)

其中min为取小，μi(e)和μj(ec)分别为e和ec的隶属度。在某一采样时刻，根据偏差和偏差变化的测量值，采用面积重心法解模糊，可求得此时ΔKP的值为：

(20)

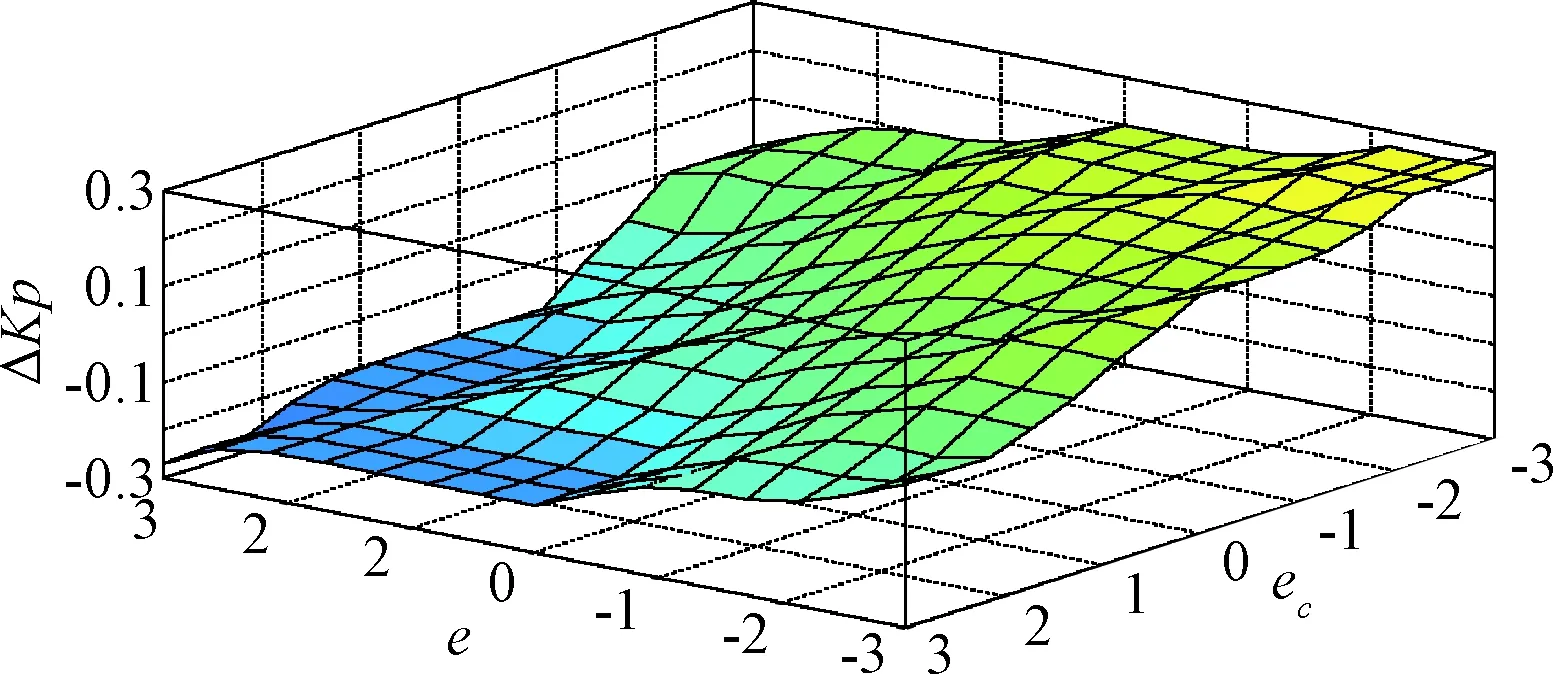
图14 ΔKP 的模糊规则三维图Fig.14 3D graph of the fuzzy rule of ΔKP

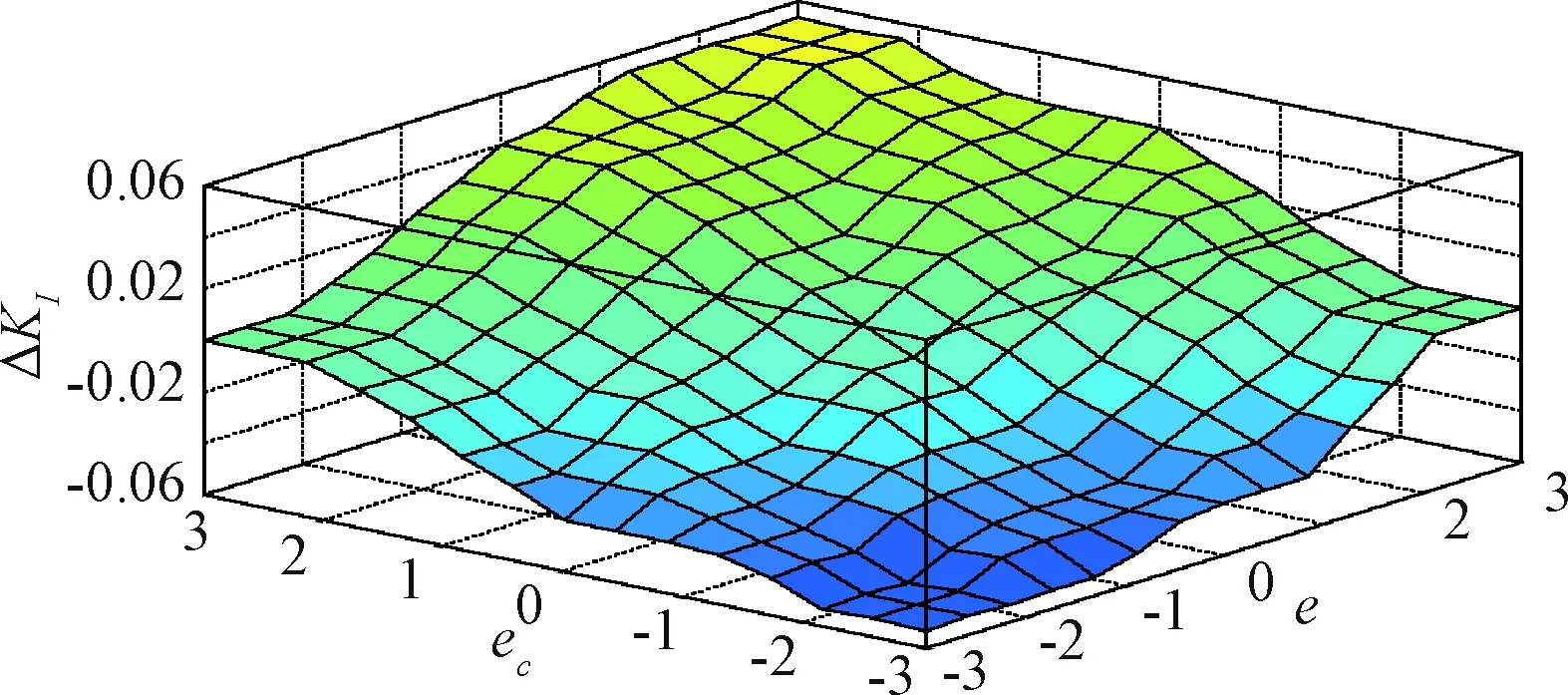
图15 ΔKI 的模糊规则三维图Fig.15 3D graph of the fuzzy rule of ΔKI

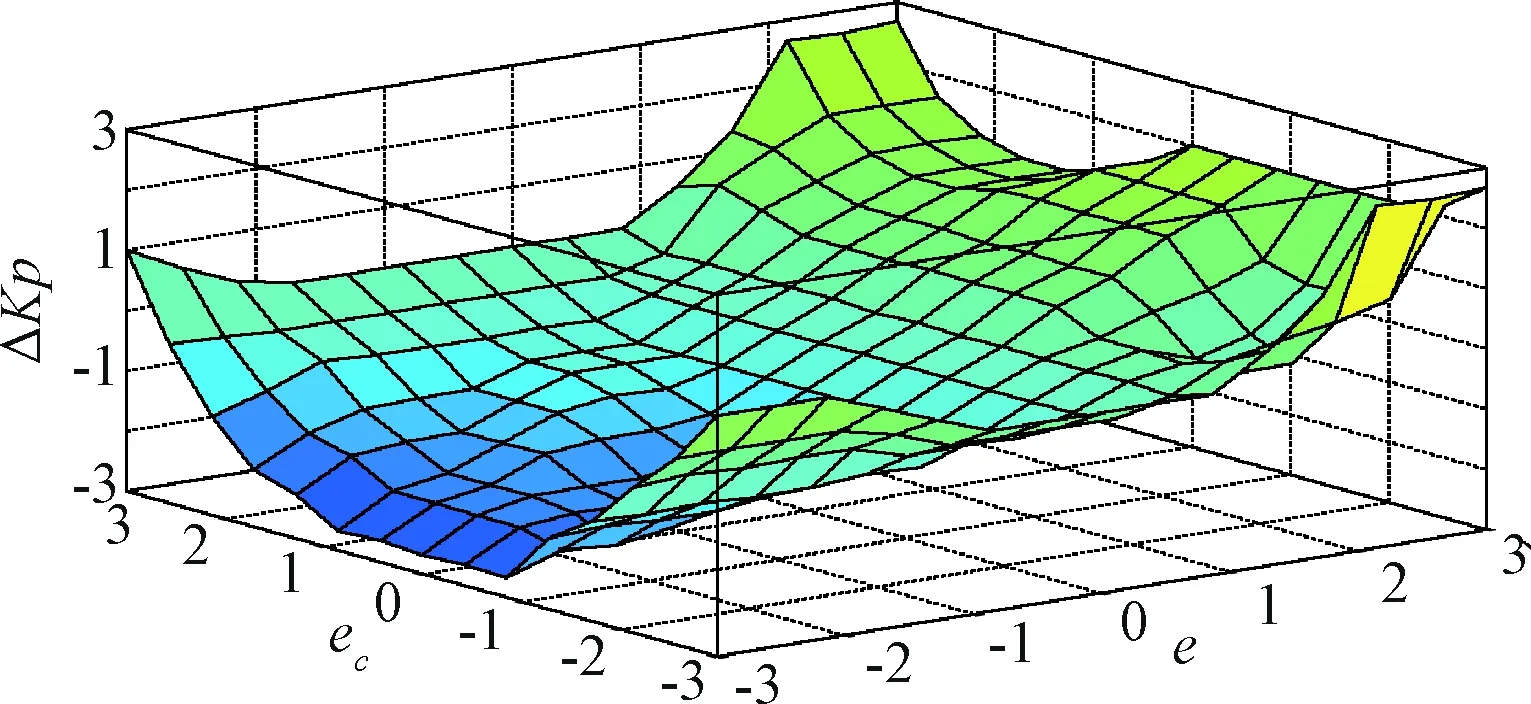
图16 ΔKD 的模糊规则三维图Fig.16 3D graph of fuzzy rule of ΔKD

考核信号取阶跃信号考察性能指标, 分别对采用模糊PID控制器和PID控制器的控制系统进行了仿真，其跟踪仿真实验结果如图17所示：

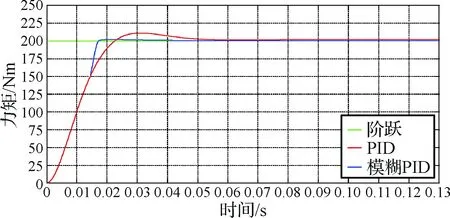
图17 传统PID和模糊PID阶跃响应对比Fig.17 Comparison of step response between traditional PID and fuzzy PID

从图17中比较看出，相比传统PID，模糊自适应PID可以提高系统快速性和减小超调，在传统PID满足稳态精度前提下，模糊自适应PID具有更高的控制精度和适用性。

3 试验台精度考核

3.1 阶跃信号考核

以阶跃函数作为加载单元的输入信号，考核加载单元对对日定向装置施加的加载力矩的性能指标，采用的跃函数的时域表达式为

(21)

其中R为力矩指令。由实验结果得到数据如表2所示：

根据力矩指令幅值的改变，观察系统的动态响应。根据图表2数据变化规律，可得出：加载单元有很好的动态性能，其暂态性能指标均满足实验要求。系统的阶跃曲线接近加载单元自身的阶跃曲线，并且随着输入力矩幅值的增加，输出的过渡时间变长，超调减小。

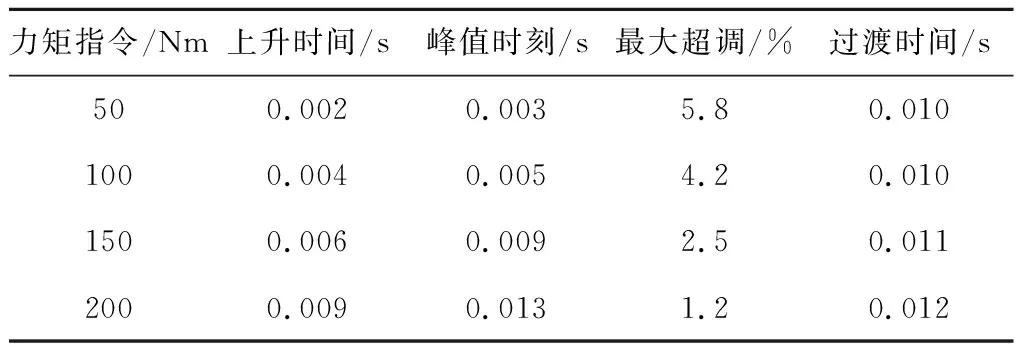
表2 阶跃响应性能Table 2 Step response performance

3.2 正弦信号考核

加载单元对正弦载荷的模拟难度较大，对加载单元输入幅值为100 Nm，频率为1～10 Hz的正弦力矩，考核加载单元的响应速度、带宽及稳定性。采用输入力矩和实测力矩之间的幅值偏差和相角偏差作为加载单元的跟踪性能考察指标，试验结果如表3所示。

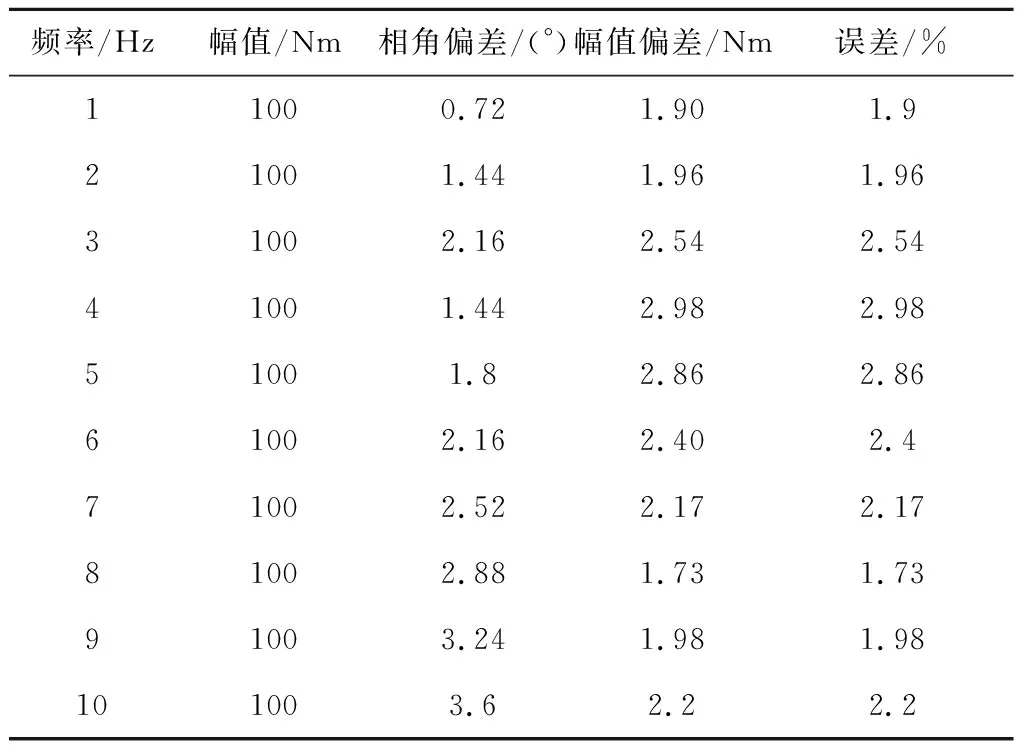
表3 不同频率正弦考核幅值相角偏差Table 3 Amplitude deviations and phase deviations under the different frequency sinusoidal loading

从试验结果可以看出，最大幅值偏差为2.2%，最大相角差出现在系统考察频段的上界10 Hz处，滞后角度为3.6°，跟随误差较小，满足试验精度要求。说明加载单元可以为空间站对日定向装置提供0～10 Hz较高精度的期望负载力矩模拟太阳电池帆板对对日定向装置的挠性负载力矩，以考察对日定向装置的驱动性能。

3.3 扭振系统模型考核

通过对加载单元输入扭振系统模型的输出曲线，考核加载单元的对期望负载力矩的跟随性能，实验得出在指令力矩振幅为5 Nm，不同频率下力矩的幅值和相角的偏差如表4所示：

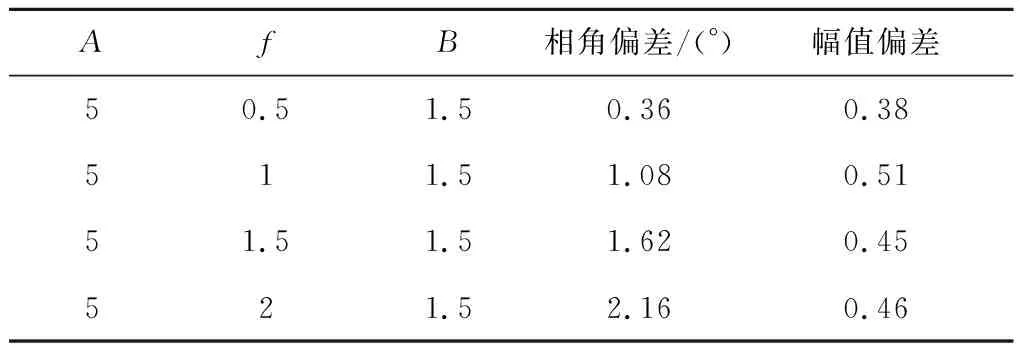
表4 扭振考核工况Table 4 Torsional vibration assessment

在频率为1 Hz、振幅为5 Nm工况下测量的扭振力矩曲线和幅值偏差曲线由图18和图19所示：

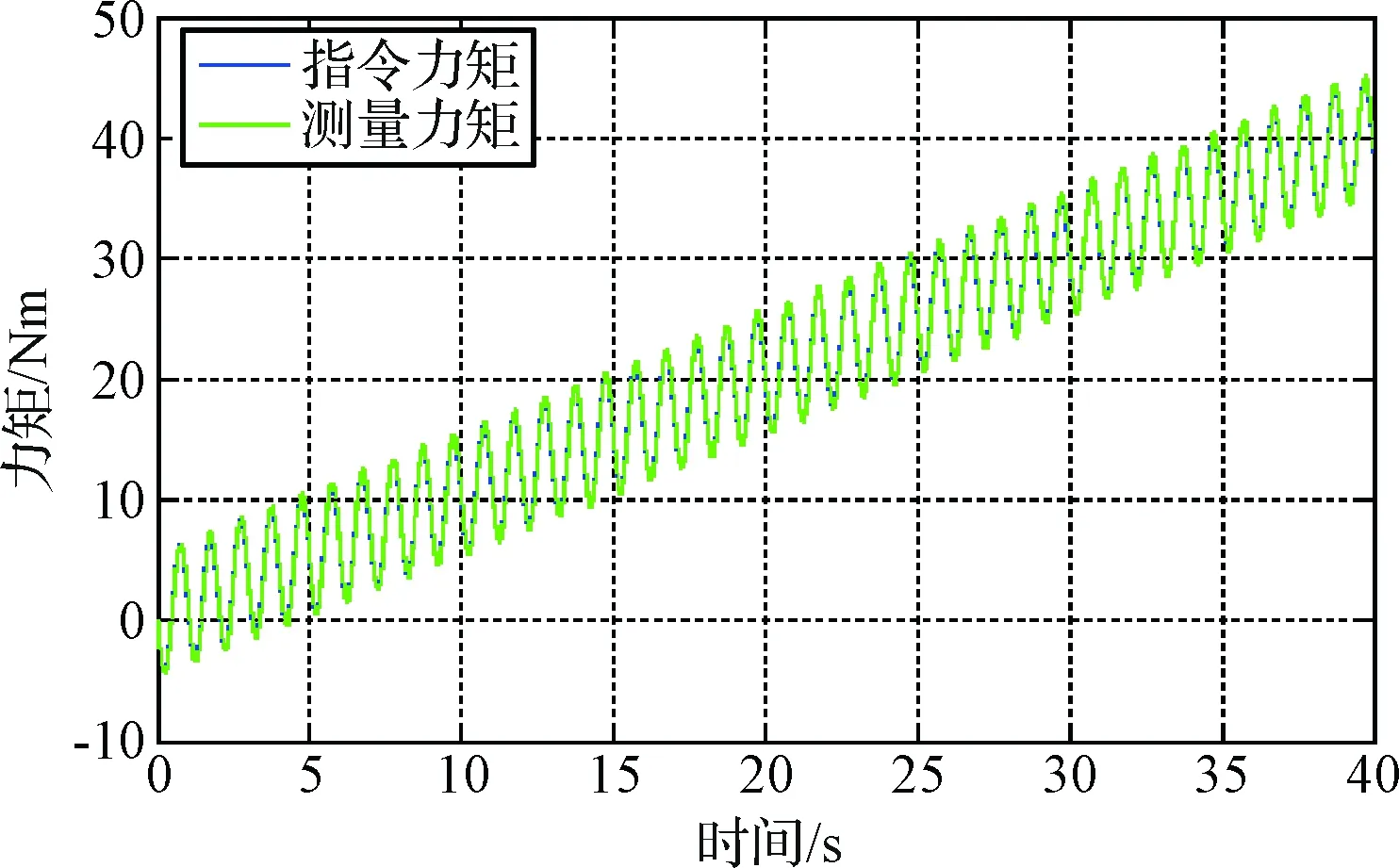
图18 扭振系统力矩实测曲线Fig.18 Torque measurement curve of torsional vibration system

可以得出加载单元对扭振系统模型的输出加载力模拟效果良好，幅值偏差小于1%和相角偏差小于2.1°，加载单元的可以较为准确的为对日定向装置施加以扭振系统模型的输出力矩。

3.4 帆板模型考核

利用耦合系数法建立太阳帆板柔性动力学模型，其中动力学模型的输入为对日定向装置的驱动加速度信息，输出为模型实时计算的加载力矩指令，利用帆板模型输出实时力矩作为加载单元的输入，对其跟随性能进行考核，实测曲线如图20和图21所示，加载力矩对输入力矩跟随误差很小，不超过1 Nm，可较为精确地模拟太阳电池帆板模型作用于对日定向装置的期望挠性负载力矩，进而满足对日定向装置对太阳电池帆板模型的驱动性能的考核实验要求。

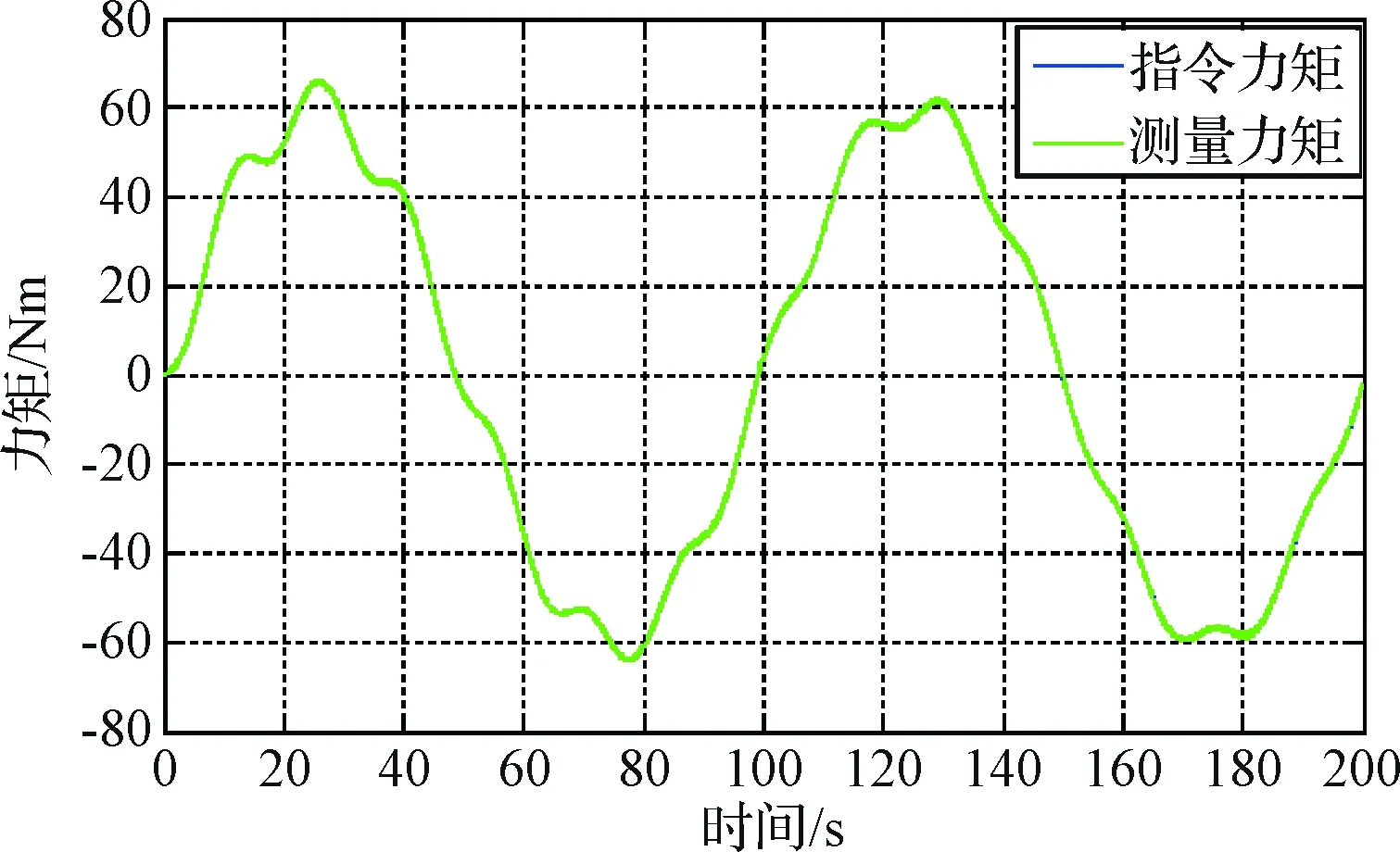
图20 帆板模型加载曲线Fig.20 Loading curve of windsurfing model

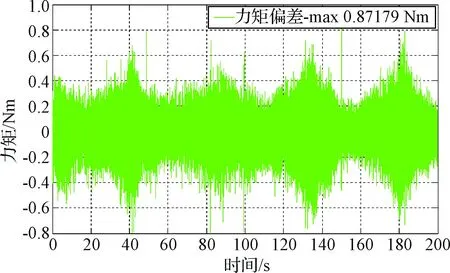
图21 帆板模型偏差曲线Fig.21 Deviation curve of windsurfing model

4 结 论

为考察空间站对日定向装置的对太阳电池帆板的驱动性能，本文建立了电动负载模拟器模型，模拟太阳电池帆板对对日定向装置的挠性负载力矩。为提高作用于对日定向装置的加载单元输出力矩对太阳电池帆板模型负载力矩的跟随精度，本文通过递推最小二乘法，对加载单元的参数进行了辨识，建立了加载单元模型，采用一种基于超前校正环节和模糊自适应PID的复合控制算法设计了半物理试验台控制器，采用仿真与试验交叉校验的方式，对控制器的各个环节参数进行了修正，最后通过试验对加载单元对对日定向装置的力矩加载精度进行考核。实验结果表明，该复合控制算法有效提高了空间站对日定向装置半物理试验台的加载性能，系统在频率为0～10 Hz范围内的加载力矩的幅值偏差小于3%，相角滞后小于3.6°，扩展了加载单元的加载带宽、提高了对模拟负载力矩跟随精度，加载单元较好的复现了太阳电池帆板模型作用于对日定向装置的负载力矩，为对日定向装置的驱动性能考核产生较为理想的测试力矩。

参 考 文 献

[1] 贺云, 尹猛, 徐志刚, 等. 对日定向半物理试验台的加载有效性验证[J]. 宇航学报, 2017, 38(02): 198-204. [He Yun, Yin Meng, Xu Zhi-Gang, et al. Effectiveness validation of the semi-physical test bench for the sun orientation. Journal of Astronautics[J]. Journal of Astronautics, 2017, 38(2): 198-204.]

[2] 程俊波, 张强, 虎刚, 等. 基于复合控制器的卫星帆板驱动机构的控制[J]. 计算机仿真, 2016, 33(01): 81-85. [Cheng Jun-bo, Zhang Qiang, Hu Gang, et al. The control of high stability SADA based on a composite controller[J]. Computer Simulation, 2016, 33(01): 81-85.]

[3] 斯祝华, 刘一武, 黎康. 太阳帆板驱动装置建模及其驱动控制研究[J]. 空间控制技术与应用, 2010, 36(02): 13-19. [Si Zhu-hua, Liu Yi-wu, Li Kang. Research on modeling and driver design of solar array drive assembly[J]. Aerospace Control and Application, 2010, 36(02): 13-19.]

[4] Lu D, Liu Y. Singular formalism and admissible control of spacecraft with rotating flexible solar array[J]. Chinese Journal of Aeronautics, 2014, 27(1): 136-44.

[5] 周通,郭宏,徐金全. 基于输入成形的太阳能帆板自适应滑模控制[J]. 北京航空航天大学学报, 2018,44(04):737-745.[Zhou Tong, Guo Hong, Xu Jin-quan, Adaptive sliding mode control of solar array with input shaping[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018,44(04):737-745]

[6] Li H Q, Liu X F, Duan L C, et al. Deployment and control of spacecraft solar array considering joint stick-slip friction[J]. Aerospace Science and Technology, 2015, 42: 342-352.

[7] Li H Q, Duan L C, Liu X F, et al. Deployment and control of flexible solar array system considering joint friction[J]. Multibody System Dynamics, 2017, 39(3): 249-265.

[8] 王德章. 三维挠性附件模拟器控制系统的设计与实现[D]. 哈尔滨: 哈尔滨工业大学, 2016. [Wang De-zhang. Design and implementation of control system of three dimensional flexible appendage simulator[D]. Harbin: Harbin Institute of Techno-logy, 2016.]

[9] Kwak M K, Heo S, Kim H B. Dynamics of satellite with deployable rigid solar arrays [J]. Multibody System Dynamics, 2008, 20(3): 271-286.

[10] 尹猛, 徐志刚, 白鑫林, 等. 基于气浮的卫星挠性旋转帆板物理仿真系统设计[J]. 空间科学学报, 2017, 37(03): 338-343. [Yi Meng, Xu Zhi-gang, Bai Xin-lin, et al. Design of physical simulation system for satellite flexible rotating panels based on flotation[J]. Chinese Journal of Space Science, 2017, 37(03): 338-343.]

[11] Ding X L, Li X, Xu K, et al. Study on the behavior of solar array deployment with root hinge drive assembly[J]. Chinese Journal of Aeronautics, 2012, 25(2): 276-284.

[12] Jorgensen J, Louis E L, Hinkle J D, et al. Dynamics of an elastically deployable solar array: ground test model validation [C]. 46th AIAA/ASME/ASCE/AHS/ASC Structures, Struct-ural Dynamics and Materials Conference, Austin, Texas, April 18-21, 2005.

[13] Scherpen J, Van D, Klaassens J, et al. Nonlinear control for magnetic bearings in deployment test rigs: Simulation and experimental results[C]. Proceedings of the 37th IEEE Conference on proceedings of the Decision and Control, Tampa, USA, December 18-18, 1998.

[14] Meguro A, Shintate K, Usui M, et al. In-orbit deployment characteristics of large deployable antenna reflector onboard Engineering Test Satellite VIII[J]. Acta Astronautica, 2009, 65(9): 1306-1316.

[15] Ren Z P, Liu L P. Influence of the Zero-gravity Test Facility on the Solar Array′s Deployment Test[J]. Spacecraft Engineering, 2008, 17(6): 73-78.

[16] Li T, Wang Y. Performance relationships between ground model and space prototype of deployable space antennas[J]. Acta Astronautica, 2009, 65(9): 1383-1392.