多航天器反步滑模SO(3)协同控制
马鸣宇,董朝阳,马思迁,王 青
(1. 北京航空航天大学航空科学与工程学院, 北京 100191;2. 北京电子工程总体研究所, 北京 100854;3. 北京航空航天大学自动化科学与电气工程学院, 北京 100191)
0 引 言
多航天器系统通过航天器之间信息交互和协同工作组成,与传统的单个航天器相比,具有成本低、研制周期短、应用方式灵活等优点,可以更为有效地进行工作,在深空探测[1]、交会对接[2]、对地测量[3]方面更具应用价值。姿态协同是指通过设计恰当的协同控制律,对航天器之间的相对姿态进行协调,使各航天器姿态保持一致,进而完成复杂任务。在航天器控制领域,姿态协同具有重要的研究意义和广泛的应用前景[4-6]。
在协同控制问题中,多航天器系统模型由每个航天器的姿态描述和相互之间的拓扑组成,需要根据航天器之间的通信拓扑利用相邻航天器的状态信息构造控制器,是一种分布式的控制方法[7]。在此情形下,文献[8]结合反步法在解决多变量解耦非线性控制方面的优势,提出多欧拉-拉格朗日系统的协同跟踪方法。文献[9-10]研究了多航天器编队的有限时间控制问题。适用于多个航天器的抗饱和容错控制等问题在文献[11]得到研究。文献[12]结合二阶多智能体一致性协议,提出多航天器编队循环追踪算法。但在现有的大部分文献[8-15]中,姿态通常采用俯仰/偏航/滚转三通道角度模型[13]、四元数模型[11]和罗格里德参数(MRPs)[12,14-15]来描述,而这三种模型均存在有一定的局限性:欧拉角表示方法在姿态角360°大范围变化时会产生奇异,使得采取角度模型所设计的控制器只适用于一定范围内。四元数方法避免了角度更新过程中的奇异问题,但四元数到旋转矩阵的映射不具有惟一性,在控制过程中可能导致姿态散开,引起系统性能下降[16-17]。MRPs模型也同样存在非全局与不唯一问题。考虑到这些不足,文献[18]提出了基于特殊正交群(Special Orthogonal Group, SO(3))的姿态建模与控制方法。针对单个体控制对象,文献[18]基于SO(3)研究了3D摆的姿态控制问题,文献[19]进一步结合SO(3)模型提出面向航天器的跟踪与全局镇定方法。文献[20]提出采用旋转矩阵描述姿态的单个航天器跟踪控制方法,克服了姿态展开现象。文献[21]考虑单个无人机的姿态大角度跟踪问题,设计了SO(3)滑模变结构姿态控制器。文献[22-23]研究了李群上多个刚体的姿态建模问题,但要求拓扑是强连通或是无向的。SO(3)方法能够进行整体描述从而使模型和设计过程得到简化,相比传统区分通道分别设计的方法更为统一,且不存在姿态动力学中的奇异问题,更适用于多航天器协同控制。
值得注意的是,基于SO(3)的相关控制方法目前仍有一些问题需要解决:一是现有的SO(3)方法多考虑的是以单个航天器为对象的控制问题,而对于多个航天器SO(3)协同控制的研究还比较有限,而SO(3)误差具有多种不同形式[24],在存在信息交互的多航天器系统中SO(3)指令和控制器形式都需要重新设计;二是SO(3)方法虽然能够避免姿态动力学更新过程中的奇异问题,在指令和实际姿态相差180°时误差方程中会出现矩阵不可逆的情形[25],使得现有SO(3)控制器大多为误差的线性反馈形式[26-27],限制了非线性方法的应用。滑模控制方法具有收敛速度快、动态性能好等优点,因此在文献[9-10,28-29]都取得有效的应用。但是,如前文所述,这些文献中的滑模控制方法均在四元数或MRPs基础上提出,存在一定的局限。同时,SO(3)的特殊性使得滑模方法很难直接应用于多航天器SO(3)姿态模型。
为了解决这些问题,本文考虑将SO(3)模型引入多航天器系统,提出基于SO(3)的姿态协同控制方法。注意到SO(3)形式与传统姿态描述不同,文中首先对多航天器系统中SO(3)协同指令进行研究,根据通信拓扑结构设计了一种采用旋转矩阵形式的姿态指令,进一步定义了SO(3)上的协同误差。为避免控制器奇异,结合反步法思想采用不同的滑模面得到了SO(3)非线性协同控制器,并给出了稳定性证明。文中使用包含五个航天器的协同控制系统对所提方法进行了仿真,仿真结果与理论分析相符,校验了基于SO(3)协同控制方法能够避免奇异问题,实现多航天器稳定的姿态协同。
1 多航天器姿态协同系统建模
1.1 航天器SO(3)模型
在三维空间中,航天器本体坐标系与惯性系之间的转换关系可以使用一个正交变换矩阵R来表示,而这些正交变换矩阵构成了特殊正交群SO(3):
SO(3)={R∈R3×3|RRT=I3,detR=1}
(1)
对于给定的航天器姿态均对应SO(3)中的一个元素R,即航天器的姿态可以通过R进行建模。设Ω=[ω1ω2ω3]T,定义hat映射为:
(2)
hat映射将任意三维向量映射为三维反对称矩阵。其逆运算称为vee映射,记为∨:
(3)
根据以上定义,考虑含有N个航天器的协同控制系统,其中第i个航天器的姿态模型可以描述为:
(4)
式中,R∈SO(3)为航天器本体坐标系到惯性坐标系的旋转矩阵,Ωi∈R3为航天器的角速度,Ji∈R3为航天器的转动惯量,Mi∈R3为控制输入力矩。
1.2 航天器通信拓扑描述

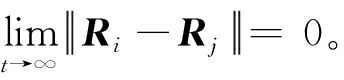
2 SO(3)姿态协同指令设计与误差方程
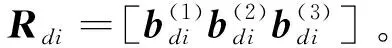
(5)
(6)
(7)
在得到协同指令Rdi后,需要将实际姿态Ri与指令信号Rdi之间的误差转换到R3空间中以构造控制器。由vee映射定义SO(3)中姿态误差为:
(8)
同时,由于
(9)
选取角速度误差eΩi为
(10)
基于上述SO(3)中姿态误差模型,下面对误差的状态方程进行推导。
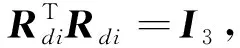
(11)
进一步,对eRi求导并代入可得:
(12)
同样,对eΩi求导可得:
(13)
(14)
3 基于反步滑模的SO(3)控制器设计
在非线性模型和的基础上,记:
(15)
(16)
则航天器i的SO(3)误差模型可以用如下方程表示:
(17)
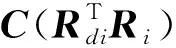
(18)
式中,
γi(t)=
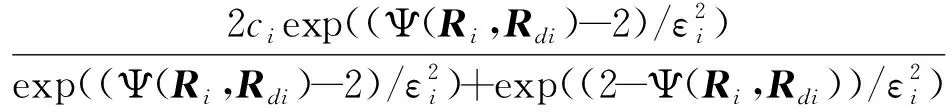
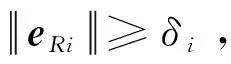
(19)
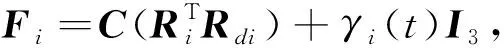
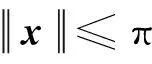
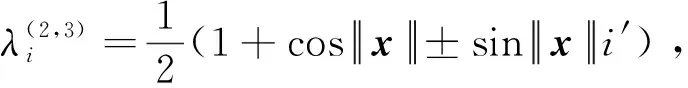
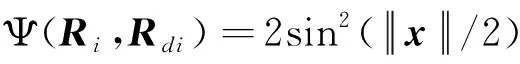
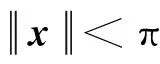
于是,该步的虚拟控制量就可以设计为:
(20)
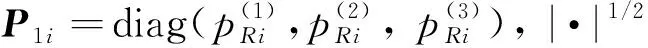
考虑对虚拟控制量的跟踪误差,选取滑模面s2i为:
(21)
(22)
(23)
(24)
选取期望的滑模面趋近律为:
(25)
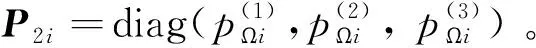
Mi= -Ji(K2is2i+P2i|s2i|1/2∘sgn(s2i)+
(26)
(27)
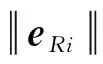
Mi= -Ji(K2is2i+P2i|s2i|1/2∘sgn(s2i)+
(28)
4 协同稳定性分析
在本节中,以定理的形式给出了所提SO(3)协同控制方法的稳定性结论。
定理1. 考虑N个航天器组成的系统(4),若航天器之间的通信拓扑包含生成树,那么根据所设计的协同指令(5)-(7)与滑模控制器(26)和(28),多航天器系统能够实现指令跟踪,达到稳定的姿态协同。
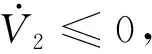
证. 证明主要分为两个部分,首先证明滑模控制器能够完成对协同指令信号的有效跟踪,进一步证明所设计的协同指令和控制器能够实现多航天器之间有效的姿态协同。
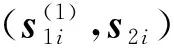
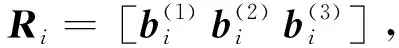
(29)
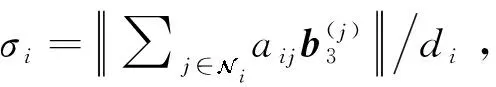
(30)
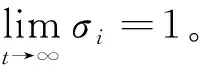
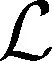
(31)
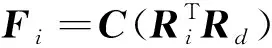
注2. 面向多航天器的SO(3)控制方法研究了与针对个体的SO(3)方法有较大不同。除了要考虑自身状态以外,有向拓扑结构的出现使得指令与控制器的设计需要利用有限的相邻航天器状态信息。此外的不同之处在于,在基于SO(3)的协同控制问题中还需要研究有效的协同指令。而姿态指令Rdi的设计要求在能够使得航天器实现协同的同时,须满足Rdi属于SO(3)的条件,而通常在姿态角或四元数模型中采用相邻航天器信息线性组合的方式不满足此要求。因此,在文中在考虑协同指令时,在式(5)-(7)中对Rdi各列向量进行向量积运算,保证向量之间的正交性后做归一化处理,使得Rdi∈SO(3)。得这也是多航天器协同控制设计所需要解决的关键步骤。
5 仿真校验
为了验证所设计的基于SO(3)的协同控制器的有效性,在本节中给出两个算例进行仿真分析。
算例1 在本算例中,考虑由5个航天器组成的协同控制系统,各航天器的参数和初始值在表1中给出。
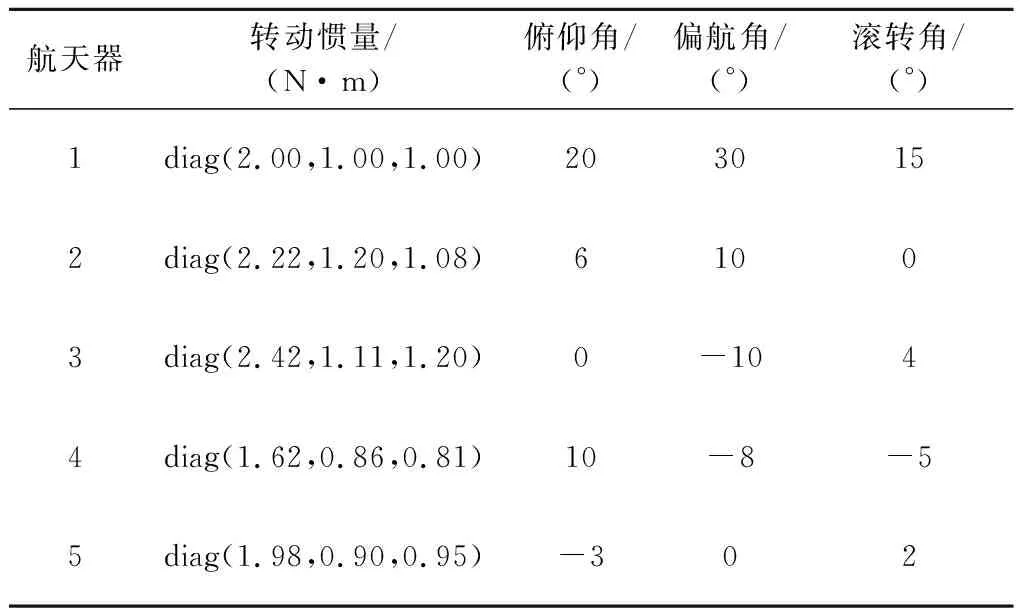
表1 航天器参数与初始条件Table 1 Parameters and initial conditions of spacecraft
初始姿态对应的R阵为:
航天器之间的有向通信拓扑如图1所示。对应的图为:a14=0.58,a23=0.33,a25=0.11,a32=0.25,a41=0.21,a43=0.4,a51=0.37。
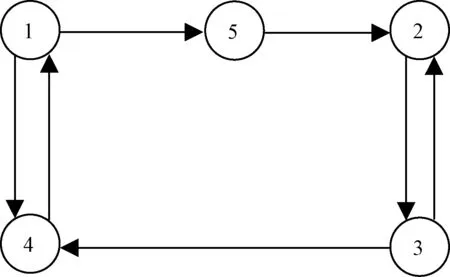
图1 航天器之间的通信拓扑Fig.1 Communication topology between spacecrafts
进一步,采用文中所设计的控制器和进行仿真。控制器参数设置为:K1i= diag(1.15, 1.15, 1.15),K2i=diag(0.15,0.15,0.15),P1i= 10-2×diag(3, 3, 3),P2i= 10-2×diag(3, 3, 3)。仿真结果在图2~图5中给出。
需要注意的是,在控制器设计与仿真过程中,姿态均使用SO(3)中的R矩阵来表示,而为了方便结果展示,文中将R转换成姿态角度:图2~图4分别给出了各航天器俯仰、偏航和滚转角随时间变化曲线。从图2~4中可以看出,在初始姿态角度小于90°时,各航天器能够以较快速度收敛实现姿态协同。
文中以航天器5为例在图5中给出了其控制输入的变化情况,其它航天器与之类似。由图可见航天器控制力矩符合实际情况,在约10 s后收敛为0,与姿态变化趋势相符,协同性能良好。
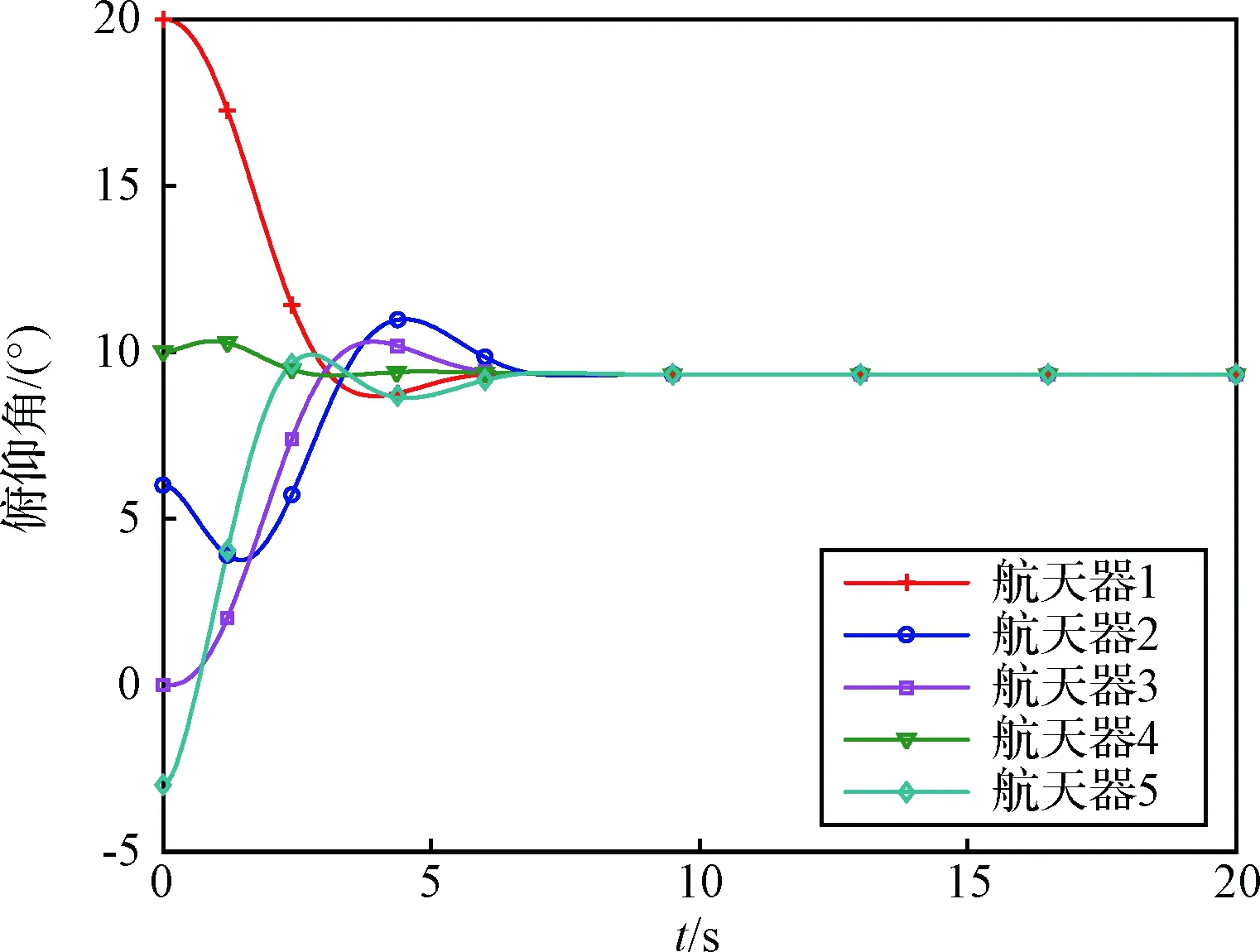
图2 各航天器俯仰角变化曲线Fig.2 Illustration of the pitch angles of spacecraft
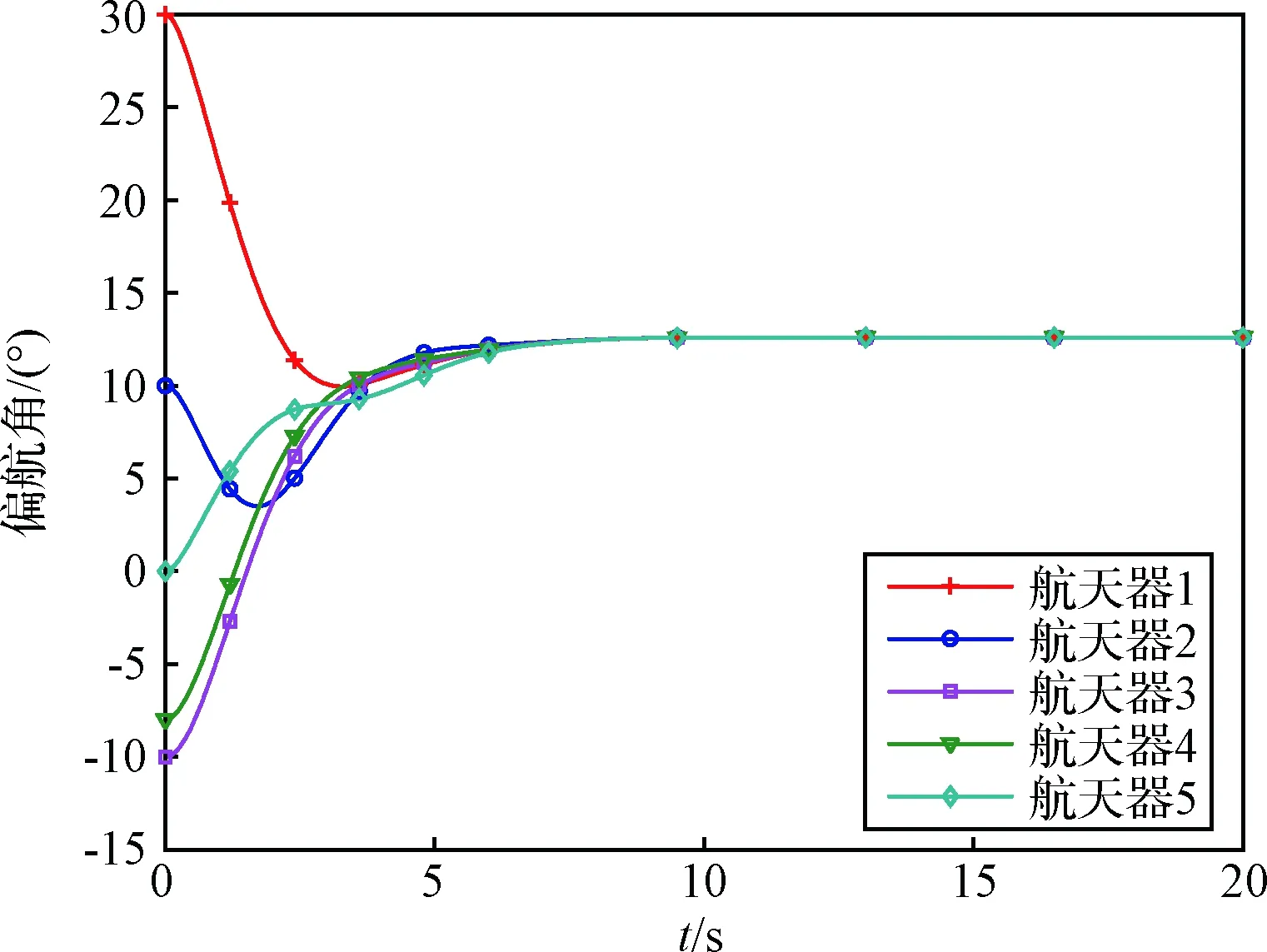
图3 各航天器偏航角变化曲线Fig.3 Illustration of the yaw angles of spacecraft
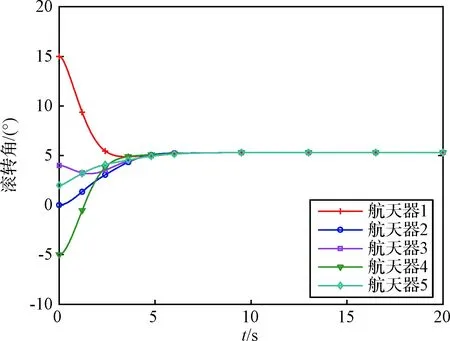
图4 各航天器滚转角变化曲线Fig.4 Illustration of the roll angles of spacecraft
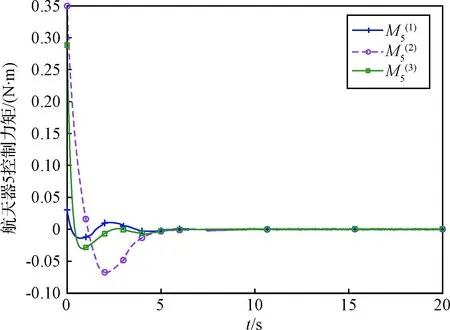
图5 航天器5的控制力矩Fig.5 Control input of the 5th spacecraft
为了定量描述姿态协同的准确程度,引入协同误差函数Qa来表示多航天器之间的姿态差异,而通过Qa值的变化反映协同控制效果。定义Qa为:
(32)
式中,εi=ri-r1,ri=[θiψiφi]T,θi、ψi和φi分别为航天器的俯仰角、偏航角和滚转角。同时,为了说明本文基于SO(3)协同控制方法的优势,文中采用相同初始条件和参数进行了对比仿真,如图6所示。其中,方法1为本文方法;文献[11]基于四元数模型采用了滑模控制器,记为方法2;方法3为文献[6]中使用MRPs姿态模型的有限时间协同控制方法。
从图中可以看出,姿态协同误差随着时间的增长逐渐收敛为0,说明各航天器实现了姿态协同。各个方法的Qa收敛到1°的时间分别为4.89 s,5.15 s和9.29 s,验证了所设计的SO(3)滑模控制方法的快速性和有效性。
算例2 进一步,为了验证所提出的SO(3)协同控制方法在航天器姿态大范围变化时的适用性和优势,在本算例中进一步设置各航天器具有较大的初始姿态,且航天器之间相对姿态相差较远。算例2中各航天器的初始值在表2中给出,拓扑结构等其他参数与算例1中相同。
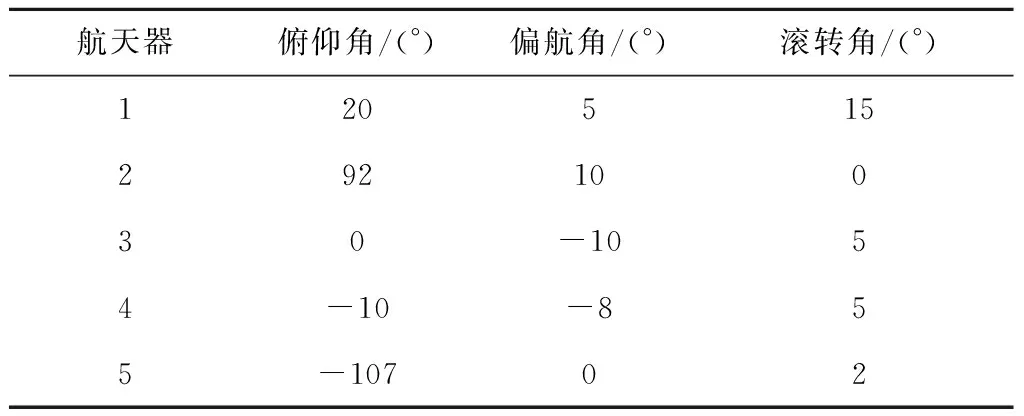
表2 航天器初始条件Table 2 Initial conditions of spacecraft
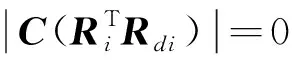
针对此时大姿态角度的情形,同样将仿真结果转换为姿态角并在图6~图9中给出,控制输入曲线在图10中给出。需要注意的是,在传统方法中采用姿态角描述姿态时,为了保证姿态与角度的一一对应,通常定义[30]俯仰角θ∈(-180°,180°],偏航角ψ∈(-90°,90°],滚转角φ∈(-180°,180°]。在此种定义下,即使相邻两个时刻姿态是连续变化的,但由于定义范围的限制,在运行过程中也可能会出现姿态角度“跳变”的情况。如图8所示,航天器2的偏航角在仿真开始后逐渐减小,在0.5 s附近由于达到定义域下界而产生了“跳变”,同时引起滚转角发生变化以满足定义域要求。
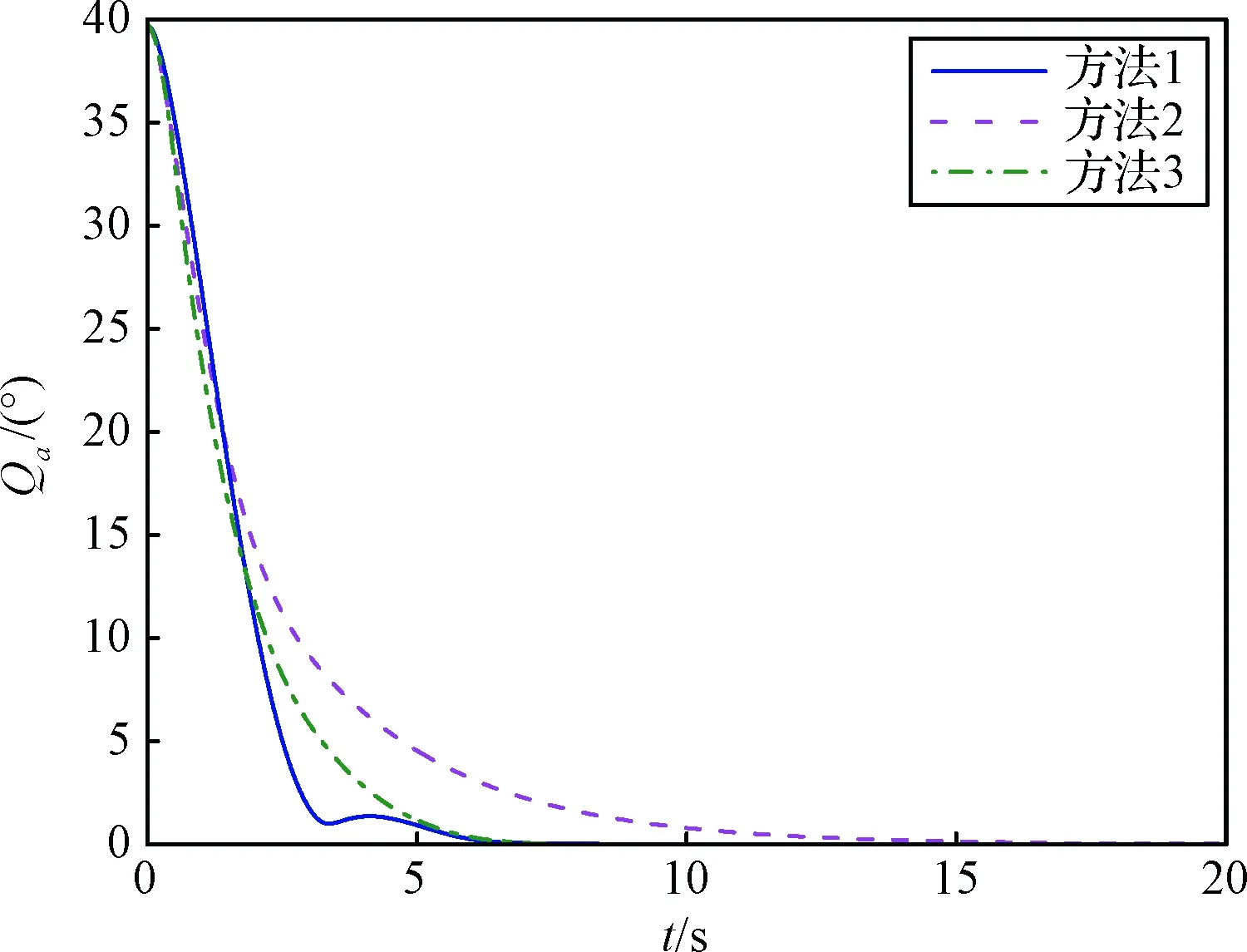
图6 姿态误差Qa对比曲线Fig.6 Comparative results of the attitude errors Qa
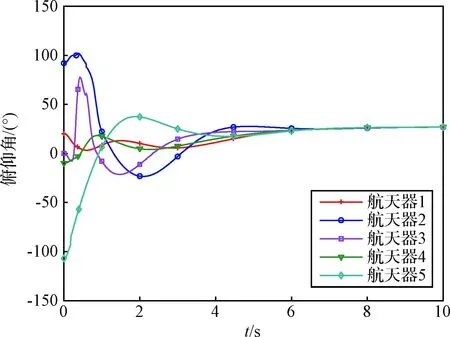
图7 各航天器俯仰角变化曲线Fig.7 Illustration of the pitch angles of spacecraft
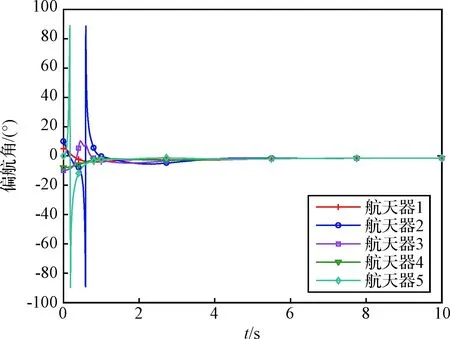
图8 各航天器偏航角变化曲线Fig.8 Illustration of the yaw angles of spacecraft
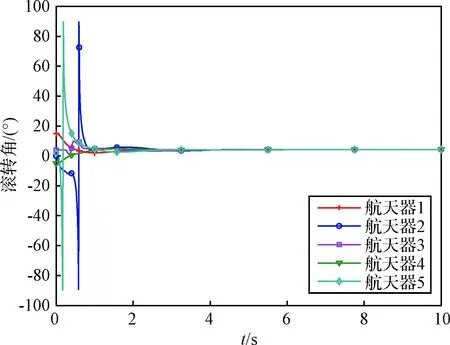
图9 各航天器滚转角变化曲线Fig.9 Illustration of the roll angles of spacecraft
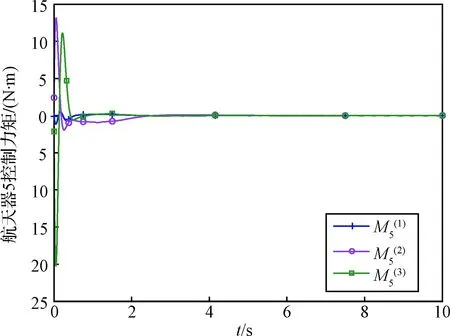
图10 航天器5的控制力矩Fig.10 Control input of the 5th spacecraft
作为对比,图11中给出了采用R∈SO(3)描述的航天器姿态变化情况。记Rij为R中的第i行第j列的元素,由于R23包含了三通道姿态角的信息,因此选取R中的元素R23进行观察。从图11中可以看出实际上航天器的姿态并未发生“跳变”,是连续变化的。相比之下,图8中的姿态角不连续是由于其定义范围造成的,而在姿态角大范围变化时出现的“跳变”情况会使得传统基于姿态角的控制器很难继续有效工作。这也对比说明了SO(3)方法的优势。结合图7至图10可以看出,本文提出的基于SO(3)的协同控制避免了奇异问题,在航天器大姿态角运动时仍能够实现稳定的姿态协同,验证了所设计方法的适用性和有效性。
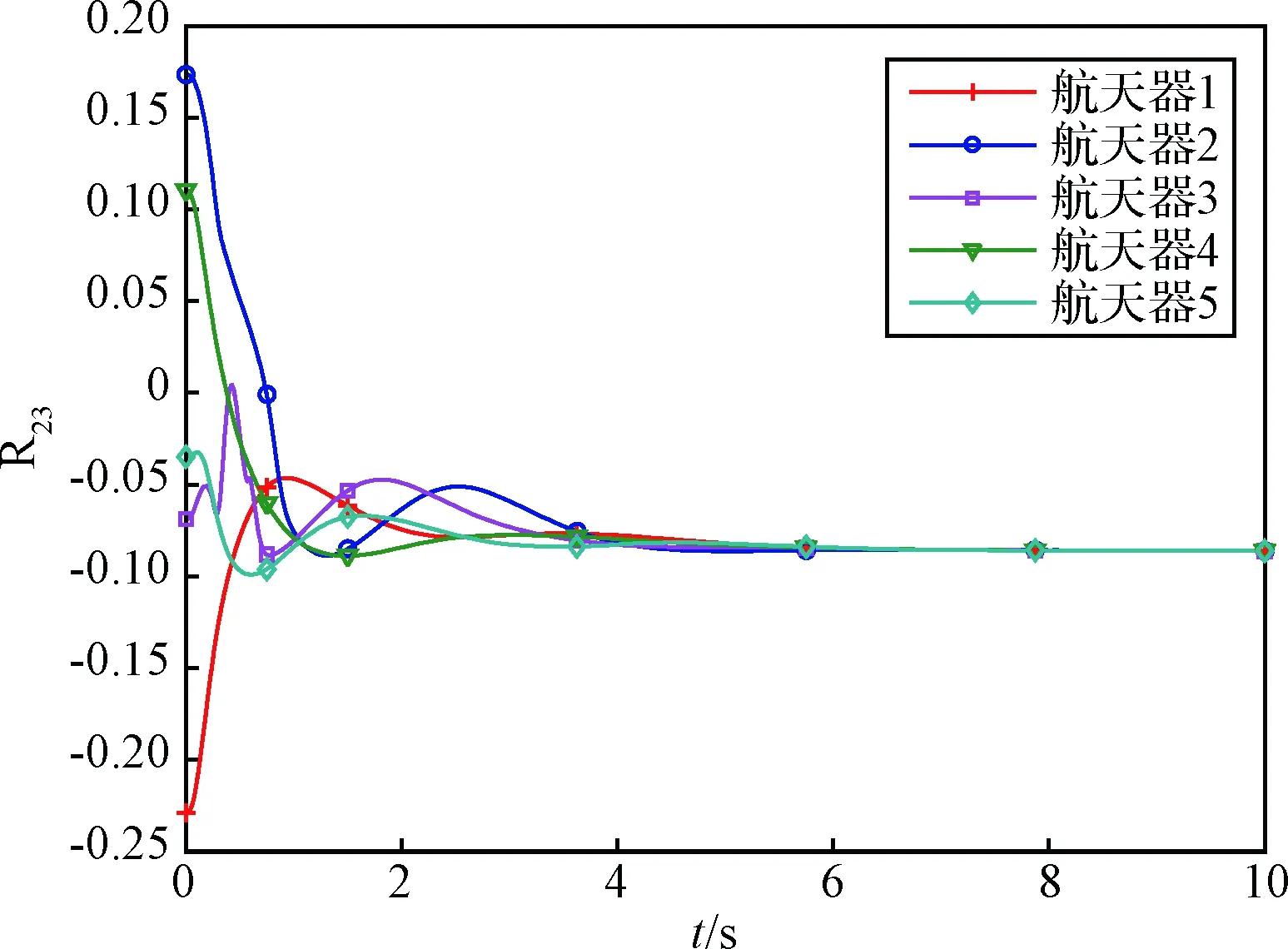
图11 采用SO(3)描述的航天器姿态变化曲线Fig.11 Attitudes of spacecraft on SO(3)
6 结 论
本文在考虑有向通信拓扑的情况下,建立了多航天器系统SO(3)非线性模型。利用相邻航天器的状态信息设计了旋转矩阵形式的姿态协同指令,并在保证指令属于SO(3)群的基础上,给出了SO(3)协同误差表示。进一步结合反步法,在协同误差较大时,采用无奇异滑模面构造非线性协同控制器;而在协同误差较小时,切换到无补偿项的滑模面以使得误差快速收敛到零,保证了姿态全局范围内的无奇异性和收敛性。仿真结果验证了本文方法能够有效地实现多航天器姿态协同。
参 考 文 献
[1] 曲成刚, 曹喜滨, 张卓, 等. 行星表面多漫游器编队探测系统的分布式H∞控制器设计[J]. 宇航学报, 2015, 36(5): 539-548. [Qu Cheng-gang, Cao Xi-bin, Zhang Zhuo, et al. DistributedH∞controller design for planetary multirover formation[J]. Journal of Astronautics, 2015, 36(5): 539-548.]
[2] 梁斌, 高学海, 潘乐, 等. GEO编队空间机器人系统交会方法[J]. 宇航学报, 2016, 37(2): 182-188. [Liang Bin, Gao Xue-hai, Pan Le, et al. A formation rendezvous method of space robotic system for on-orbit service of GEO[J]. Journal of Astronautics, 2016, 37(2): 182-188.]
[3] 张保群, 宋申民, 陈兴林. 考虑控制饱和的编队飞行卫星姿态协同控制[J]. 宇航学报, 2011, 32(5): 1060-1069. [Zhang Bao-qun, Song Shen-min, Chen Xing-lin. Attitude coordination control of formation flying satellites under control saturation[J]. Journal of Astronautics, 2011, 32(5): 1060-1069.]
[4] Zheng Z, Xu Y, Zhang L, Song S. Decentralized attitude synchronization tracking control for multiple spacecraft under directed communication topology[J]. Chinese Journal of Aeronautics, 2016, 29(4): 995-1006.
[5] Chen T, Wen H, Hu H, Jin D. Distributed finite-time tracking for a team of planar flexible spacecraft[J]. ISA Transactions, 2017, 69: 214-221.
[6] 张海博, 胡庆雷, 马广富, 等. 多航天器系统分布式有限时间姿态协同跟踪控制[J] 控制与决策, 2014, 29(9):1593-1598. [Zhang Hai-bo, Hu Qing-lei, Ma Guang-fu, et al. Distributed finite-time attitude coordinated tracking control for multiple spacecraft systems[J]. Control and Decision, 2014, 29(9): 1593-1598.]
[7] 王婷, 张羽飞. 等质量立体五星库仑编队飞行的分析与控制[J]. 宇航学报, 2015, 36(11): 1279-1288. [Wang Ting,Zhang Yu-fei. Analysis and control for three dimensional five-satellite coulomb formation flight in geostationary earth orbit[J]. Journal of Astronautics, 2015, 36(11): 1279-1288.]
[8] Sun Y, Wang W, Ma G, et al. Backstepping-based distributed coordinated tracking for multiple uncertain Euler-Lagrange systems[J]. Journal of Systems Engineering and Electronics, 2016, 27(5): 1083-1095.
[9] Lyu J, Qin J, Ma Q, et al. Finite-time attitude synchronisation for multiple spacecraft[J]. IET Control Theory & Applications, 2016, 10(10): 1106-1114.
[10] Ran D, Chen X, Misra A K. Finite time coordinated formation control for spacecraft formation flying under directed communication topology[J]. Acta Astronautica, 2017, 136: 125-136.
[11] Huang D, Wang Q, Duan Z. Distributed attitude control for multiple flexible spacecraft under actuator failures and saturation[J]. Nonlinear Dynamics, 2017, 88(1): 529-546.
[12] 罗建军, 周亮, 蒋祺祺, 等. 航天器编队的六自由度循环追踪协同控制[J]. 宇航学报, 2017, 38(2): 166-175. [Luo Jian-jun, Zhou Liang, Jiang Qi-qi, et al. 6 DOF coordinated control using cyclic pursuit for spacecraft formation[J]. Journal of Astronautics, 2017, 38(2): 166-175.]
[13] Du H, Zhu W, Wen G, Wu D. Finite-time formation control for a group of quadrotor aircraft[J]. Aerospace Science and Technology, 2017, 69: 609-616.
[14] Yang H, You X, Hua C. Attitude tracking control for spacecraft formation with time-varying delays and switching topology[J]. Acta Astronautica, 2016, 126: 98-108.
[15] Zhang K, Demetriou M A. Adaptation and optimization of the synchronization gains in the adaptive spacecraft attitude synchronization[J]. Acta Astronautica, 2015, 46: 116-123.
[16] 何朕, 王广雄. 姿态控制中的散开现象[J]. 机电与控制学报, 2015, 19(7):101-105. [He Zhen, Wang Guang-xiong. Unwinding phenomenon in attitude control[J]. Electric Machines and Control, 2015, 19(7): 101-105.]
[17] Mayhew C G, Sanfelice R G, Teel A R. Quaternion-based hybrid control for robust global attitude tracking[J]. IEEE Transactions on Automatic Control, 2011, 56 (11): 2555-2566.
[18] Chaturvedi N A. Global Dynamics and Stabilization of Rigid Body Attitude Systems[D]. Ann Arbor: University of Michigan, 2007.
[19] Sanyal A, Fosbury A, Chaturvedi N, et al. Inertia-free spacecraft attitude tracking with disturbance rejection and almost global stabilization[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(4): 1167- 1178.
[20] 郑重, 宋申民. 基于旋转矩阵描述的航天器无角速度测量姿态跟踪无源控制[J]. 控制与决策, 2014, 29(9): 1628-1632. [Zheng Zhong, Song Shen-min. Rotation matrix based passive attitude tracking control of spacecraft without angular velocity measurements [J]. Control and Decision, 2014, 29(9): 1628-1632.]
[21] 刘锦涛, 吴文海, 李静, 等. 四旋翼无人机SO(3)滑模变结构姿态控制器设计[J]. 控制与决策, 2016, 31(6): 1057-1064. [Liu Jin-tao, Wu Wen-hai, Li Jing, et al. Sliding mode variable structure attitude controller design of quadrotor UAVs on SO(3)[J]. Control and Decision, 2016, 31 (6): 1057-1064.]
[22] Weng S X, Dong Y, Yang T C. Coordinated attitude motion control of multiple rigid bodies on manifold SO(3)[J]. IET Control Theory and Applications, 2013, 7(16): 4984-1991.
[23] Hatanaka T, Igarashi Y, Fujita M, et al. Passivity-based pose synchronization in three dimensions[J]. IEEE Transactions on Automatic Control, 2012, 57(2): 360-375.
[24] Lee T. Exponential stability of an attitude tracking control system on SO(3) for large-angle rotational maneuvers[J]. Systems and Control Letters, 2012, 61 (1): 231-237.
[25] Fernando T, Chandiramani J, Lee T, et al. Robust adaptive geometric tracking controls on SO(3) with an application to the attitude dynamics of a quadrotor UAV[C]. The 50th IEEE Conference on Decision and Control and European Control Conference, Florida, USA, December 12-15, 2011.
[26] Lee T. Global exponential attitude tracking controls on SO(3)[J], IEEE Transactions on Automatic Control, 2015, 60(10): 2837-2842.
[27] Dong R, Geng Z. Consensus based formation control laws for systems on Lie groups[J]. Systems & Control Letters, 2013, 62(2): 104-111.
[28] 张永合, 梁旭文, 张健, 等. 无阻力双星串行编队相对位置有限时间控制[J], 宇航学报, 2015, 36(8): 923-931. [Zhang Yong-he, Liang Xu-wen, Zhang Jian, et al. Finite-time relative position control for drag-free dual-satellite serial-formation[J]. Journal of Astronautics, 2015, 36(8): 923-931.]
[29] Wu B, Wang D, Poh E K, Decentralized sliding-mode control for attitude synchronization in spacecraft formation[J]. International Journal of Robust and Nonlinear Control, 2013, 23: 1183-1197.
[30] 吴森堂, 费玉华. 飞行控制系统[M]. 北京: 北京航天航天大学出版社, 2005: 56-58.

