面向飞行器总体设计的UMDO技术综述

赵 民，刘百奇，粟 华

(1. 中国运载火箭技术研究院，北京 100076；2. 中国运载火箭技术研究院研发中心，北京 10076；3. 陕西省空天飞行器设计重点实验室，西北工业大学，西安 710072)

0 引 言

进入21世纪以来，随着社会经济的进步，航空航天领域取得了突飞猛进的发展。一方面，传统飞机、导弹、火箭等飞行器面临着跨代发展机遇；另一方面，高超声速武器、重复使用空天飞行器、空间机动平台等新概念飞行器不断涌现，使现代飞行器总体设计的复杂程度和设计维度呈几何增长。这些因素对飞行器的系统性能、可靠性、研制周期及研制成本提出了更高要求[1-3]，迫切需要发展更为先进的飞行器总体设计方法以支撑未来发展[5]。多学科设计优化(Multidisciplinary Design Optimization，MDO)是一种针对复杂系统的综合优化设计方法，通过分析并利用各个学科的耦合效应与协同机制，寻求系统的综合性能最优[6-7]。目前，该方法在工程结构、飞行器设计等领域已经得到了初步应用[8-9]。

传统MDO主要处理确定性多学科设计优化(Deterministic MDO，DMDO)问题[10]，在飞行器的设计、研制及试验过程中，假设各种参数及条件都是确定性的。实际上，材料属性、载荷环境、几何尺寸、制造环境等都包含大量随机因素，建模过程中的各种假设也会引入认知模糊，导致这两类不确定性普遍存在，降低了系统可靠性并增加了设计风险。传统工程设计方法通过考虑设计裕度和保留设计余量来确保系统的可靠性，严重依赖设计经验，难以适应未来发展需求。为满足复杂耦合系统高可靠性、高安全性要求，UMDO技术逐渐发展为飞行器领域重点关注的前沿技术之一[2],[5],[11-15]。

UMDO的核心思想是采用量化方法来有效管理设计过程中的不确定性因素，在保证安全性、可靠性的前提下深度挖掘设计裕度，提升设计质量。UMDO在传统MDO的基础上进一步考虑不确定性因素的影响，结合不确定性分析方法和优化技术，通过多学科协同优化以获取系统的稳健可靠最优解。国内外众多科研机构将UMDO作为现代先进飞行器总体设计的支撑技术之一，开展重点研究。美国国家航天航空局(NASA)于2002年发表了《UMDO应用于飞行器设计的机遇和挑战》，深入分析UMDO应用于飞行器设计的需求和困难，为UMDO应用研究提供了思路和方向[5]；美国Sandia国家实验室将原子能领域的不确定性研究成果推广应用于工程系统不确定性设计，系统地研究了不确定性的分类、定义、分析和建模[16]；美国空军研究实验室(AFRL)在《空军基于能力的科技战略2030》中聚焦未来长期挑战(FLTC)，对集成系统的可靠性提出了设计要求；美国国防高级研究计划局(DARPA)于2015年启动了“定量化物理系统的不确定性”项目(EQUIPS)，旨在通过发展数学工具和方法来解决复杂系统设计问题，以有效的定量、传递和管理多源的不确定性影响。国内外许多大学也开展了UMDO研究，并取得了大量研究成果。

目前，不确定性研究可分为基于概率理论和非概率理论两类。基于概率理论的不确定性建模、分析和优化设计发展较为完善[17-18]，但受限于估计概率分布所需的数据样本容量。非概率理论因其具有处理“数据不充足、认知不充分”问题的优势受到较多关注[19-20]。实际上，由于工程问题的复杂性，单一理论都无法独立解决。因此，综合应用概率和非概率理论的随机/认知混合不确定性条件下的UMDO理论成为当前研究热点[10,21-25]。虽然UMDO在理论研究方面取得了较多成果，但在面向工程应用时仍面临以下困难：

(1)建模复杂性。飞行器系统工程不仅需要考虑设计、制造和使用过程中客观存在的随机不确定性，还要考虑由于人的主观认识不足或信息缺乏而导致的认知不确定性。对于随机不确定性，存在如何准确估计分布函数参数和验证分布模型合理性的问题；对于认知不确定性，存在如何建立不确定性因素的非概率模型问题。因此，对不确定性源的认知与建模是解决建模复杂性的关键。

(2)求解复杂性。在UMDO寻优过程中不仅要考虑不确定性的传递影响，在每个优化搜索点还需要执行耗时的不确定性分析以计算可靠性和稳健性，计算成本极大增加。目前，解决求解复杂性的研究主要集中于三个方面：一是研究不确定性的传播与量化方法，以提高不确定性分析的效率；二是研究灵敏度分析方法和优化策略，滤除对系统影响较小的不确定性变量，减少迭代次数；三是研究UMDO的过程分解技术，以提高UMDO过程的组织与协调性能。

围绕以上难点，本文从不确定性源建模、不确定性灵敏度分析、多学科不确定性分析、鲁棒性多学科优化设计4个方面梳理UMDO研究的技术体系，并结合飞行器总体设计流程与应用需求，提出UMDO在飞行器各主要设计阶段的应用模式。最后，结合我国飞行器总体精细化设计能力的发展需求，分析了目前UMDO在工程应用过程中存在的问题和未来的发展设想。

UMDO问题定义

UMDO通过在MDO中引入不确定性变量，将原来只追求性能最优化的MDO问题转变为满足稳健性和可靠性要求下的寻求性能最优化的UMDO问题。根据稳健性和可靠性需求的不同，UMDO可以分为基于可靠性的MDO(Reliability Based MDO，RBMDO)和基于稳健性的MDO(Robust MDO)。

当考虑满足约束的可靠性时，包含n个学科的RBMDO问题的数学模型可以表示为：

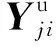
当考虑满足约束和目标函数的稳健性时，包含n个学科的RobustMDO问题的数学模型可表示为：

其中，μf和σf分别为目标函数f的均值和标准差；μgi和σgi分别为约束函数gi的均值和标准差；ki>0是由设计者给定的安全因子。

1 UMDO技术体系

对于一个飞行器UMDO问题，首先需要分析整个总体设计过程中可能存在的不确定性因素，对不确定性源进行建模和量化，构建UMDO问题；通过不确定性灵敏度分析预测影响飞行器可靠性的各输入变量之间的相对重要程度，对不确定性分析、预测与优化提供指导；考虑多学科耦合特性，分析不确定性因素对模型输出影响的分布特征；最后，基于鲁棒性不确定性优化设计，获取满足鲁棒性约束的综合性能最优解。针对上述设计流程，UMDO的技术体系可归纳为如下四个方面。

1.1 不确定性源建模

准确、可靠地描述不确定性因素是构建UMDO问题的关键之一，必须对不确定性源的构成、建模和量化开展深入研究。不确定性源建模指通过合适的数学方法对设计优化中涉及的不确定性因素进行描述和量化，根据不确定性因素的类型，采用相应的不确定性理论进行建模。

美国Sandia国家实验室将不确定性分为可认知不确定性和不可认知不确定性，并采用证据理论对混合不确定性进行了建模[26]；Hazelrigg[27-28]研究了仿真模型中可能存在的误差，将其划分为数学模型误差、计算仿真误差、模型参数误差和计算误差；Delaurentis[29]将飞行器设计不确定性分为操作/环境层、系统层和学科层不确定性三类；Padmanabhan[30]从MDO角度出发将不确定性分为变化型、决策型和建模型不确定性三类；刘宝碇等[31]将不确定性划分为随机性、模糊性、粗糙性、模糊随机性、随机模糊性等多种类型。

目前，被广泛认可的是将不确定性分为随机型和认知型两大类。其中，随机不确定性的参数建模方法有概率论、数理统计、贝叶斯统计和随机过程理论；认知不确定性通常需要根据具体特点选择相应的非概率数学工具[50-51]进行描述，如证据理论[26,34-36]、模糊集理论[37-39]、可能性理论[40]、区间数理论[20,24-25,41-44]、凸集理论[19-20,45]等。对于随机与认知不确定性同时存在的情况，通常需要采用混合建模方法，如基于模糊随机理论的不确定性混合建模方法[46]、基于概率与证据理论的不确定性混合建模方法[47-48]等。常用不确定性理论如表1所示。上述各种不确定性建模方法从不同角度给出了不确定性的度量标准，由于工程问题较为复杂，实际使用时应根据不确定性源的特点选择最为适合的建模方法。

1.2 不确定性灵敏度分析

不确定性建模需要大量的数据支撑，在设计过程中引入过多的不确定性因素会造成巨大的分析与计算成本。因此，在UMDO中需要对不确定性因素进行灵敏度分析以提供搜索方向或辅助变量筛选。不确定性灵敏度分析包括局部灵敏度分析和全局灵敏度分析两类。局部灵敏度分析用于确定可靠度或

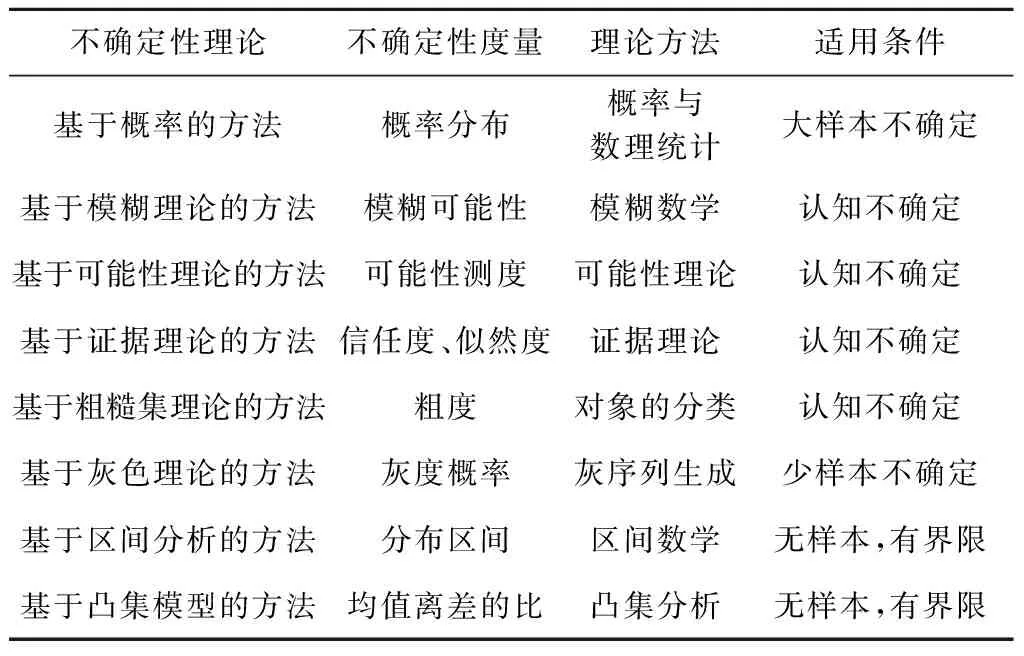
表1 不确定性理论Table 1 Uncertainty theory

某一状态变量在当前点邻域内对各不确定性变量的偏导数信息，以此对UMDO寻优提供搜索方向，提高搜索效率；全局灵敏度分析又被称为重要性测度分析，用于量化模型本身与模型输入中各项可变因素对模型输出变化的影响程度[49]，对各不确定性因素的重要性进行排序，滤除不重要因素，降低UMDO问题的复杂度。

对不确定性灵敏度分析的研究目前主要集中在随机不确定性的概率灵敏度分析方法，如微分方法、响应面方法、方差分解方法、傅里叶振幅灵敏度测试方法、抽样仿真方法等[50-52,54]。其中，抽样仿真方法，只需对不确定性变量空间进行抽样和仿真获取样本数据，简单易行而被广泛应用；分析方法包括相关系数、回归分析、方差分解等[50,55]。相关系数法只能构建线性灵敏度关系，适应性不强，回归分析在非线性程度较高时误差较大，均不适合于多学科耦合造成的高非线性不确定性问题；方差分解方法精度较高，但计算成本较大。对于大计算量仿真模型的不确定性灵敏度分析问题[52-53]，伴随方法(Adjoint Sensitivity Analysis Procedure, ASAP)是一种有效的计算方法，如果伴随模型与原始模型同步分析，ASAP仅需要少量的额外计算，适合于复杂工程应用情况。关于认知不确定性的灵敏度方法主要包括基于证据理论发展的抽样仿真方法[56-57]和解析微分方法[58]。Guo等[59-60]提出了通过证据理论计算可信性和似然性测度之间的差距的方法，以量化不确定性分布的影响大小。

全局灵敏度分析方法目前研究较少，通常都是将整个系统作为黑箱子处理以避免多学科耦合带来的影响，并不适用于学科较多、计算消耗大的情况，因此需要结合MDO求解架构的特点发展多学科下的全局灵敏度分析方法。

1.3 多学科不确定性分析

多学科不确定性分析是根据系统输入、系统本身及外部环境的不确定性对系统输出的不确定性分布进行量化，是不确定性优化设计的核心，也被称为多学科不确定性传播与量化。不确定性分析的实现方法可分为侵入式和非侵入式两类[61]。

侵入式方法通过对系统控制方程添加不确定性项，直接将不确定性影响纳入系统模型，不适合于无法获取分析模型的情况，主要包括多项式混沌展开[62-63]、随机有限元谱分析[64-66]、矩平衡方法[67]、协方差匹配方法[68-69]、贝叶斯网络方法[70]等。非侵入式方法将系统模型作为黑箱处理，只根据输入输出关系分析不确定性影响，无需修改系统模型，主要包括蒙特卡洛仿真、泰勒级数展开近似法、一阶可靠度法、二阶可靠度法、区间分析方法等[1]，以及基于多学科求解架构的并行子空间不确定性分析方法[71-73]、基于协同优化的隐式不确定性传播方法[74]、PADMA分布式求解框架[75]等。

不确定性分析依据建模理论可分为概率方法和非概率方法两类。由于概率论具有完善的数学理论基础，基于概率论的随机不确定性分析研究更为广泛，在实际工程应用中较为普及。混合不确定性分析方法的主要思想是分别对随机不确定性和认知不确定性的影响进行量化，然后将两者序贯执行以分析混合不确定性的综合影响。目前混合不确定分析研究较少，主要包括基于概率论和模糊集理论的可靠度上下限分析方法[76-78]、基于概率理论和区间分析的混合可靠度分析方法[79-80]等。由于飞行器设计的学科模型一般都是计算成本高、耗时长的高拟真度模型，采用嵌套执行混合不确定分析的计算成本将非常巨大。因此，需要发展更高效的混合不确定性分析方法。

1.4 鲁棒性多学科优化设计

不确定性优化设计指根据稳健性和可靠性要求，通过在设计空间搜索过程中不断调用不确定性分析，以寻求稳健可靠性最优解的优化过程。根据对目标函数和约束条件的不同要求，可分为稳健性设计和可靠性设计。当同时考虑目标函数稳健性和约束条件可靠性时，将其称为鲁棒性多学科优化设计。

稳健性设计[81]最早由日本学者Taguchi提出。其思想是在系统有不确定性输入的条件下，通过优化目标、设计参数及约束条件的合理设计，尽可能减小不确定性因素对产品质量的影响。随着稳健设计方法的不断完善[82-85]，20世纪80年代后逐步发展成为机械设计领域的重要研究方向[86]。现代稳健设计对其进一步深化，不仅追求系统性能最优化，同时把系统性能偏差最小也作为优化目标，以获得可行、稳健的综合最优解。稳健优化设计实际上是一个多目标优化问题，包括性能最优化和设计约束的稳健性。目前广泛采用的是加权求和法[87]、演化类算法[88-89]、基于偏好的规划法[90-91]、折中法[92-93]等。

可靠性设计最早出现于机械设计领域[94-95]，并随产品可靠性要求的不断提高逐步得到重视。可靠性设计需在每一个搜索点进行可靠性分析，计算复杂度剧增。求解这类UMDO问题通常有两种思路。

一种是从不确定性优化设计角度出发，将UMDO问题分解为确定性MDO问题和可靠性分析问题。在工程应用中经常采用一些近似求解方法将可靠性约束转化为等价的确定性约束条件，将不确定性优化问题转化为确定性优化问题以降低计算复杂度。这些方法包括角空间分析法[96]、最差情况分析法[97]、可靠设计空间法[98]、变化模式分析法[99]、近似极限状态函数法[100]、基于梯度的优化方法[101]等。上述等价转换并没有对设计方案的实际可靠度进行计算，因此获取优化方案可靠度的计算精度有限。另一种解决方法是将传统优化与可靠性分析的两层嵌套循环转化为一个单层循环的单层方法(Single Level Approach，SLA)，包括单层序贯优化法、单层融合优化法等。单层序贯优化法的思路是根据前一次循环的不确定性分析信息将可靠性约束转化为等价的确定性约束，以此将不确定性优化问题解耦为确定性优化与可靠性分析，通过序贯迭代求解，包括安全因子法[102](Safety Factor Based Approach，SFA)和序列优化与可靠性分析法(Sequential Optimization and Reliability Assessment，SORA)[103]等。单层融合优化法通过将内层循环搜索所得的MPP点简化为等价的简化计算公式，并作为约束条件引入外层优化，包括单层单向量(Single Loop Single Vector，SLSV)法[104]和单层双变量(Single Loop Double Vector，SLDV)法[105]。

另一种是从MDO角度出发，采用过程分解方法将原UMDO问题分解为多个并行执行的子问题，借鉴DMDO过程[8]运用多学科协同思想并行求解以提高效率。Mcallister等[106]提出不确定性CO过程，将基于一阶Talyor展开的期望值/方差概率估计方法集成于CO框架中；曹鸿钧[19]采用凸集理论对不确定性变量建模，在CO基础上提出多学科系统协同稳健优化(Collaborative Robust Optimization，CRO)方法；Gu和Renaud[74]提出了基于CO框架的隐式系统不确定性分析方法，建立了稳健协同优化(Robust Collaborative Optimization，RCO)过程；Padmanabhan和Batill[107]在CSSO方法基础上，提出将UMDO问题分解为若干独立的学科优化子问题，采用并行计算以提高求解效率；苏子健[108]在CSSO框架中集成基于二阶全局灵敏度方程的过程分解，实现了多学科下的不确定性优化设计；许林[109]将不确定性分析方法引入BLISS 2000框架，提出基于随机不确定性的BLISS优化过程；Kokkolaras[110]提出概率目标层级分析法，将ATC扩展到包含随机变量的层次系统UMDO问题求解；Liu[111]和Xiong[112]在此基础上进一步提出改进的概率目标层级分析法。

鲁棒性多学科优化设计解决了MDO无法保证最优设计点的可靠性和稳健性的问题，但计算量过大是UMDO向飞行器设计领域推广的主要瓶颈之一。因此，应结合现有工业领域需求和多学科耦合特点，在MDO原有求解架构基础上发展更为高效、精确的鲁棒性多学科优化设计方法。

2 UMDO的工程应用

由于UMDO在解决复杂多学科系统上具有独特优势，在飞行器设计领域也受到了广泛关注，并得到初步应用。Delaurentis[113]将UMDO方法引入超音速客机的概念设计，考虑气动与控制的紧密耦合，获得了优化方案；Chen[114]等将基于对策论的UMDO应用于高速民机的总体设计，通过降低各学科对其他学科的敏感度以提高各学科设计优化的灵活性；Aminpour[115]等提出了RBMDO方法，通过集成CAE软件将其应用于某客机翼型设计优化，在提高可靠性的同时降低了机翼质量；许林[109]在飞行器MEMS构件的设计优化中引入UGBLISS 2000优化过程，提高了构件的稳健性和可靠性；姚雯[4]等采用GBCSSUO方法进行卫星总体设计，给出满足稳健性和可靠性要求的最优总体方案。

虽然UMDO已经引起工业界的重视，并作为未来的重点研究方向之一。但目前并没有形成一套清晰、完成且规范的方法流程来指导UMDO技术向工业领域的推广。因此，本文以考虑不确定性的飞行器总体设计过程为研究对象，基于目前飞行器设计的设计流程和组织架构特点，提出一套面向飞行器总体设计的UMDO应用模式。

3 面向飞行器总体设计的UMDO应用模式

飞行器设计是一个复杂过程，不仅需考虑性能、成本、周期、可靠性等需求，还需考虑当前技术水平、实验条件、制造能力等客观约束，每一个环节都存在大量不确定性因素。尤其是新概念飞行器，缺乏必要的设计经验和参考数据，在设计初期存在着大量认知不确定性因素。随着设计过程的深入和试验数据的增加，一些认知不确定性因素会逐渐转化为确定性因素或模型参数的随机不确定性，而一些原来确认的不确定性因素也会因为设计过程的深入而发生变化。同时，分析模型的改变也会造成不确定性因素对系统影响的变化。因此，飞行设计过程是一个包含大量不确定性因素的复杂系统工程。

飞行器系统工程的全寿命周期包括概念设计、初步设计、详细设计、生产制造、使用运行、维护与报废六个阶段。每个阶段都会产生大量的不确定性因素，如图1所示。其中，概念设计阶段的不确定因素多为认知不确定性，初步设计阶段的不确定因素主要为随机与认知的混合不确定性，详细设计阶段的不确定因素主要为随机不确定性。因此，无法采用一套不确定性方法来实现飞行器全阶段的总体设计，需要针对各阶段的不确定性因素分布特点和设计需求，分别提出相应的UMDO应用模式。

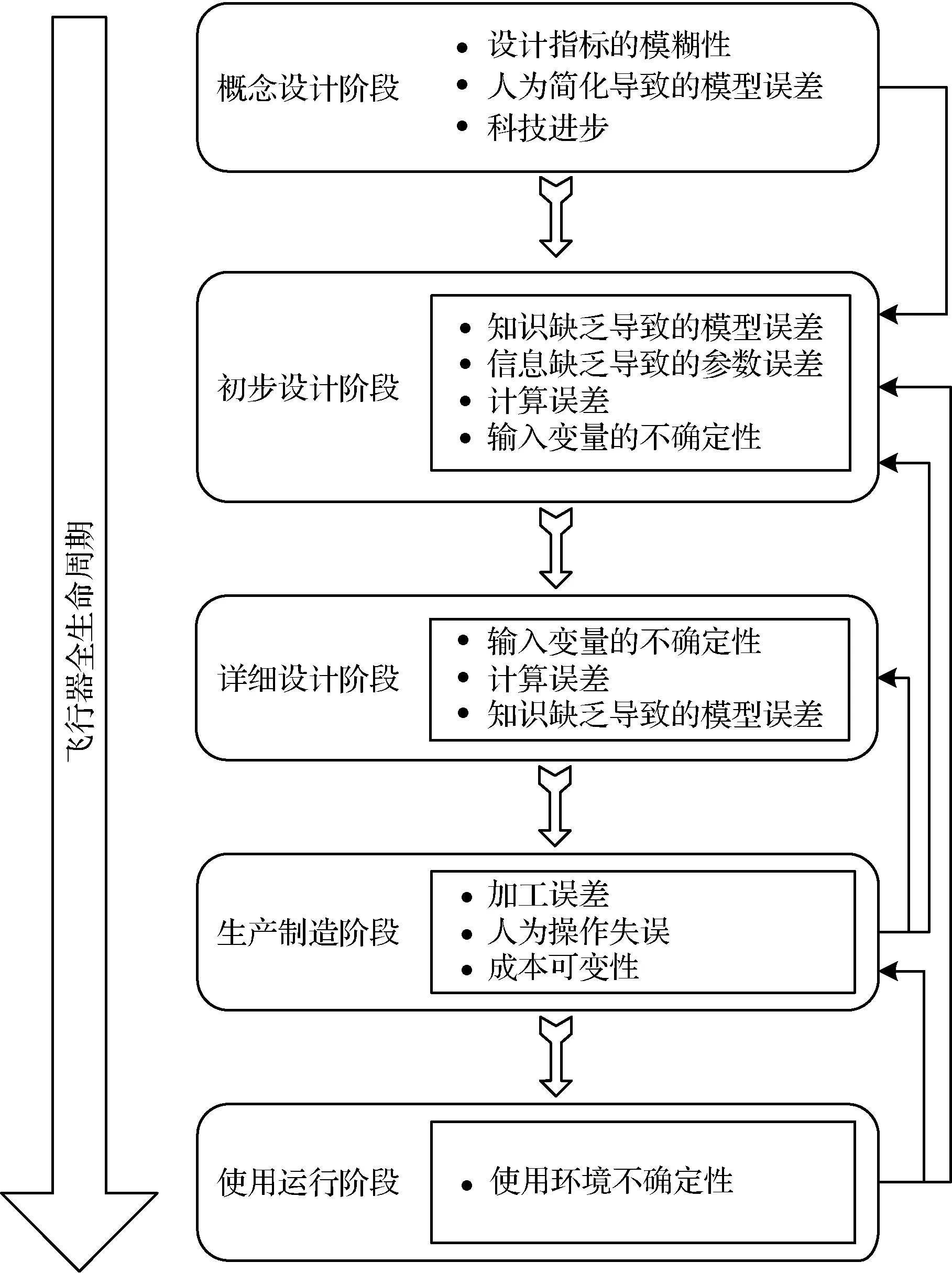
图1 飞行器各阶段的不确定性因素Fig.1 Uncertainty factors in each phase of the aircraft

3.1 概念设计阶段的UMDO流程

概念设计阶段将设计要求转化为系统要求，从而进行设计概念和方案探索，最终获得基准方案，对整个系统的研制过程和总体性能影响最大。概念设计阶段由于对设计对象认识不足，需要考虑的不确定性因素主要包括：

1)设计指标的模糊性；

2)人为简化导致的分析模型误差；

3)科技进步与技术创新引起的设计参数变化。

此阶段很多的不确定性是未知但有界的，设计者更关注设计方案的可靠性和不确定性影响下系统输出响应量的变化范围。区间模型适合于不确定信息较少、可靠性要求高的场合，因此可采用区间模型对概念设计阶段的不确定性进行描述和量化。概念设计阶段UMDO设计流程如图2所示，根据设计要求和约束条件建立符合设计需求的备选方案，基于不确定性区间模型计算各方案性能指标的变化范围，进而确定系统性能和费用，最终根据费用、风险、性能等准则选择出基准设计方案。

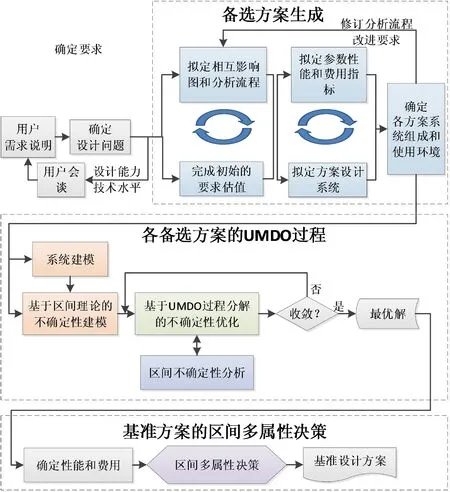
图2 概念设计阶段的UMDO设计流程Fig.2 UMDO design process of the conceptual design phase

3.2 初步设计阶段的UMDO流程

初步设计阶段的主要工作是对概念设计阶段得到的基准方案进行细节设计。在初步设计阶段的不确定性建模过程中，需要考虑的不确定性因素包括随机与认知两类不确定性。

对于随机不确定性因素，可以通过特定的随机试验来获得其变化规律，随着试验次数增加，其不确定性不会随之减少。如结构分析时的环境温度、外部载荷等外在不确定因素，以及结构尺寸、材料特性等内在不确定因素。对于认知不确定性，是指对研究对象或外部环境认知不足或数据缺少造成的不确定性，无法通过随机试验获得其变化规律。这两类不确定性的具体表现如下：

1)知识缺乏造成的数学模型和真实模型之间的差异；

2)信息缺乏造成的对给定模型参数估计的不准确；

3)离散化、舍入误差等造成的计算误差；

4)设计过程中输入变量的不确定性；

5)运行环境的不确定性；

6)加工和人为误差。

初步设计阶段的UMDO流程如图3所示。在初步设计阶段，需要依托大量的学科分析和有限的试验数据，建立基于混合不确定的系统分析模型，开展考虑混合不确定性的优化设计来优化飞行器的综合性能，从而获得满足可靠性和稳健性约束的飞行器最优方案。随着学科模型复杂度的增加，计算消耗开始成为设计过程中的主要考虑因素，可引入代理模型技术来降低UMDO的计算消耗。

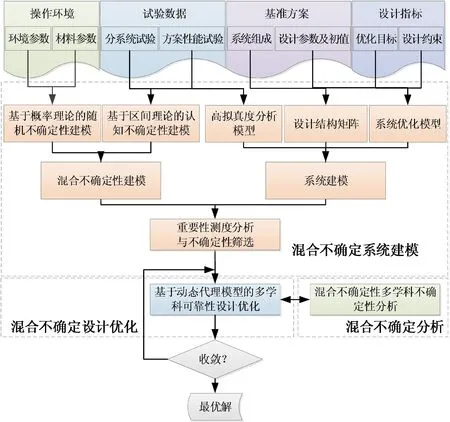
图3 初步设计阶段的UMDO设计流程Fig.3 UMDO design process of the preliminary design phase

3.3 详细设计阶段的UMDO流程

详细设计阶段主要解决管理协调的问题，尤其是各分系统之间、系统与环境之间的接口问题，还要组织周密的试验以验证新系统的性能是否满足系统的设计要求。与初步设计阶段相比，详细设计阶段包含更多的复杂学科分析，重点对各分系统、各学科进行细节优化设计，原则上不再进行总体综合优化。由于概念设计和初步设计两个阶段的设计、仿真和试验为详细设计阶段提供了大量数据，因数据不足引起的认知不确定性已转化为确定性因素或模型参数的随机不确定性。因此，该阶段重点考虑随机不确定性影响，主要包括：

1)设计输入变量的不确定性；

2)运行环境的不确定性；

3)加工和人为误差；

4)知识缺乏导致的模型误差；

5)离散化、舍入误差等导致的计算误差。

详细设计阶段将当前最优方案的总体性能和不确定性因素分配到各子系统，各子系统根据新指标进行新一轮的分系统详细设计，协调各分系统试样技术要求，完成系统综合试验及其结果分析，以校验各分系统设计的可行性，进行系统综合试验以校验系统设计是否符合设计要求，最后完成设计定型。如图4所示，详细设计阶段的设计流程由不确定系统建模、不确定指标分配和分系统详细设计三部分组成。主要采用概率理论建立随机不确定性模型，并根据初步设计阶段各分系统返回的设计结果，进行性能指标和不确定性偏差的优化分配。

图4 详细设计阶段的UMDO设计流程Fig.4 UMDO design process of the detailed design phase

4 发展展望

4.1 现存问题

UMDO从提出至今已有10余年，虽然已在航天航空等领域得到了重点关注和发展，但尚未形成完整的应用能力，在工程应用中还存在以下问题：

(1)不确定性认知问题。飞行器设计中存在着大量不确定性因素，如气动学科的几何外形、网格离散和分析工况，结构学科的结构参数、材料属性和载荷，推进学科的燃料特性和燃烧过程，弹道学科的气动数据和大气参数等不确定性因素，以及各学科计算方法的模型误差与数值误差等。如何对上述不确定性因素进行识别、区分、定义、筛选，是现代飞行器不确定性研究必须首先解决的问题。

(2)不确定性混合建模问题。不确定性因素包括客观存在的随机不确定性和认知不确定性。目前基于单一不确定性模型的UMDO已经得到较多研究，但实际工程应用问题通常都会由多种不同类型的不确定性因素构成，必须采用混合建模方式以准确地描述各类不确定性影响；同时，由于各不确定性因素之间通常并不完全独立，存在着相关性影响，在建立不确定性混合模型时还必须考虑其相关性。

(3)不确定性源在多学科复杂系统中的传播问题。传统多学科不确定性分析将整个系统作为一个整体，忽视了不确定因素在系统内部各学科之间的耦合传递过程，无法充分利用多学科耦合特性以提升复杂系统的综合性能。不确定性因素在上述耦合过程中的传播机理和耦合效应对系统的整体性能影响巨大，需结合MDO问题的多学科耦合特点研究不确定性源的传播影响，为UMDO提供支持。

(4)面向工程应用的UMDO存在着计算量大和求解效率低的问题。多变量、多约束、强耦合是工程应用问题的显著特点，与之对应的UMDO问题求解难度更大，计算消耗也更多。必须发展更高效的求解架构和算法，在确保精度的同时，将计算规模控制到可接受的程度，才能满足工程应用需求。

(5)缺乏典型应用案例。UMDO在飞机、卫星等飞行器设计的应用但仍处于探索阶段，目前UMDO难以直接应用于包含复杂学科分析模型、多学科强耦合、多变量多约束的实际工程问题中，需要结合工业部门的实际需求，基于目前的技术发展，探索更为适合的UMDO应用模式，进一步提升UMDO技术的工程应用成熟度。

4.2 研究展望

上述问题是目前UMDO应用于工程应用的主要障碍，可从如下几个方面开展后续研究：

(1)多学科下的不确定性认知。针对各学科特点，对设计过程中的不确定性因素进行识别、区分、定义和筛选，确定最佳的不确定性因素建模方法；结合多源数据融合等辅助手段，发展相关模型的参数辨识与验证技术，为不确定性分析过程提供模型和数据支持。

(2)考虑多学科耦合影响，研究多学科下的不确定灵敏度分析方法。一是借助灵敏度评估不确定性变量的重要程度，以缩减计算规模，形成动态规模下的自适应不确定性求解能力；二是探索不确定性灵敏度作为梯度信息的可行性，发展更为高效的不确定性分析方法。

(3)多学科耦合下的不确定性传播机制。结合现代飞行器的多学科耦合特点，研究不同学科之间、不同系统层次之间以及不同评价体系之间不确定性因素的传播机理和耦合效应，从分系统层面和多系统层面探索可靠性设计和稳健性设计的最佳实现途径，逐步取代基于偏差和余量的传统设计手段，进一步挖掘飞行器总体设计过程中的设计潜能。

(4)高效的UMDO求解架构。计算量过大是UMDO应用的主要阻碍之一。需结合自适应代理模型、MDO求解架构、多学科解耦等技术，发展更高效、稳健的求解架构，支持大规模UMDO问题，具备分布式并行求解能力的UMDO求解架构，以支撑UMDO的工程应用开展。

(5)开展方案设计阶段的UMDO应用研究，根据设计需求在概念设计、初步设计和详细设计阶段逐步引入UMDO来提高系统鲁棒性，以减少反复设计风险并提高综合性能。目前可将重点放在概念设计阶段和初步设计阶段，在现有MDO应用案例的基础上，结合实际工程研制环境，研究最佳的UMDO过程组织实现，探索适用于飞行器总体设计过程的UMDO设计环境与应用流程，最终形成面向综合性能最优的飞行器UMDO设计与优化能力。

5 结 论

本文论述了UMDO的研究现状，梳理了UMDO技术的发展体系并提出了面向现代飞行器总体设计的UMDO应用模式。任何一个新技术的发展都是一个逐步完善的过程，随着飞行器设计等工业领域对总体技术的不断重视，迫切需要发展更先进的设计方法和支撑技术以提升总体设计能力。UMDO正是这样一种技术，在传统MDO的基础上进一步考虑不确定性影响，在追求性能最优的同时满足鲁棒性设计要求，以符合现代工业设计对最优性能和可靠性的同时追求。

参 考 文 献

[1] 陈小前, 姚雯, 欧阳琦. 飞行器不确定性多学科设计优化理论与应用[M]. 北京: 科学出版社, 2013.

[2] 袁亚辉. 多学科设计优化及其不确定性研究[D]. 西安: 电子科技大学, 2009. [Yuan Ya-hui. Study on optimization of multidisciplinary design and its uncertainty. Xian: University of Electronic Science and Technology. 2009.]

[3] 粟华. 飞行器高拟真度多学科设计优化技术研究[D].西安: 西北工业大学, 2014. [Su Hua. Study on high fidelity multidisciplinary design optimization technique of vehicles[D]. Xian: Northwestern Polytechnical University, 2014. ]

[4] 姚雯, 陈小前, 赵勇. 基于不确定性MDO的卫星总体优化设计研究[J]. 宇航学报, 2009, 30(05):1808-1815,1833. [Yao Wen, Chen Xiao-qian, Zhao Yong. Research on satellite system design based on uncertainty multidisciplinary design optimization[J]. 2009, 30(05):1808-1815,1833.]

[5] Zang T A, Hemsch M J, Hilburger M W, et al. Needs andopportunities for uncertainty-based multidisciplinary design methods for aerospace vehicle[R]. Hampton: Lanley Research Center, 2002.

[6] 欧阳莹之. 复杂系统理论基础[M]. 上海: 上海科技教育出版社, 2002.

[7] 苗东升. 系统科学大学讲稿[M]. 北京: 中国人民大学出版社, 2007.

[8] 王振国, 陈小前, 罗文彩, 等. 飞行器多学科设计优化理论与应用研究[M]. 北京: 国防工业出版社, 2006.

[9] 王书河, 何麟书. 飞行器多学科设计优化概述[J]. 宇航学报, 2004(06): 697-701. [ Wang Shu-he, He Lin-shu. The summarization of multidisciplinary design optimization for flight vehicles[J]. 2004(06): 697-701.]

[10] 刘伟. 随机和认知不确定性条件下的多学科设计优化建模研究[D]. 电子科技大学, 2011. [Liu Wen. Study of multidisciplinary design optimization modeling under stochastic and cognitive uncertainty[D]. University of Electronic Science and Technology, 2011.]

[11] Oberkampf W L, Helton J C, Joslyn C A, et al. Challeng-eproblems: uncertainty in system response given uncertain parameters[J]. Reliability engineering and system safety, 2004, 85(1-3): 11-199.

[12] 张为华, 李晓斌.飞行器多学科不确定性设计理论概述[J]. 宇航学报, 2004(06):702-706. [Zhang Wei-hua, Li Xiao-bin. Survey on the theory of aircraft multidisciplinary uncertainty design[J]. Journal of Astronautics, 2004, 25(6):702-706. ]

[13] Matthew J D, Brian J G, et al. Effects of disciplinary uncertainty on multi-objective optimization in aircraft conceptual design[J]. Struct Multidisc Optim, 2011, 44: 831-846.

[14] Alexander W G. Enhancement ofset-based design practices via introduction of uncertainty through the use of interval methods[D]. University of Michigan, 2011.

[15] Zhang Xu-dong, Huang Hong-zhong, Xu Huan-wei. Multidisciplinary design optimization with discrete and continuous variables of various uncertainties[J]. Struct Multidisc Optim, 2010, 42: 605-618.

[16] Oberkampf W L, Deland S M, Rutherford B M. Estimation for Total Uncertainty in Modeling and Simulation[R]. SAND 2000-0824, 2000.

[17] 刘玉彬. 工程结构可靠度理论研究综述[J]. 吉林建筑工程学院院报. 2002, 19(2): 41-43. [Liu Yu-bing. A summary of structural engineering reliability theory[J]. Journal of Jilin Architectural and Civil Engineering Institute. 2002, 19(2): 41-43.]

[18] 吕震宙, 冯蕴雯. 结构可靠性问题研究的若干进展[J]. 力学进展. 2000, 30(1): 21-28. [Lu Zhen-zhou, Feng Yun-wen. Advances in structural reliability studies[J]. Advances in Mechanics. 2000, 30(1): 21-28.]

[19] 曹鸿钧. 基于凸集合模型的结构和多学科系统不确定性分析与设计[D]. 西安: 西安电子科技大学, 2005. [Cao Hong-yun. Convex-model based analysis and design for structural and multidisciplinary systems under uncertainty[D]. Xian: University of Electronic Science and Technology, 2005.]

[20] 陶友瑞. 基于凸模型的多学科不确定性优化设计方法[D]. 长沙: 湖南大学, 2010. [Tao You-rui. Multidisciplinary uncertain design optimization based on convex model theory[D]. Changsha: Hunan University, 2010. ]

[21] Elishakoff I. On the uncertain triangle[J]. The Shock and Vibration Digest. 1990, 22(10):1-10.

[22] Du Xiaoping, Sudjianto A, Chen Wei. An integrated framework for optimization under uncertainty using inverse reliability strategy[J]. Journal of Mechanical Design, 2004, 7(126): 562-570.

[23] 彭文胜, 张建国, 王丕东, 等. 混合不确定信息航天机构可靠性综合分析方法[J]. 宇航学报, 2015, 36(05): 596-604. [Peng Wen-sheng， Zhang Jian-guo, Wang Pi-dong, et al. Comprehensive reliability analysis of the aerospace mechanism with hybrid uncertainty information[J]. 2015, 36(05): 596-604.]

[24] 刘继红, 安向男, 敬石开. 随机与区间不确定性下的序列化多学科可靠性分析[J]. 计算机集成制造系统, 2013, 7(19): 1441-1446. [Liu Ji-hong, An Xiang-nan, Jing Shi-kai. Sequential multidisciplinary reliability analysis with random and interval uncertainty[J]. Computer Integrated Manufacturing Systems. 2013, 7(19): 1441-1446.]

[25] Oberkampf W L, Helton J C. Investigation of evidence theory for engineering application[R]. AIAA 2002-1569, 2002.

[26] Hazelrigg G A. System engineering: an approach to information-based design[M]. New Jersey: Prentice Hall, 1996.

[27] Hazelrigg G A. The implication of arrow’s impossibility theorem on approaches to optimal engineering design[J]. Journal of Mechanical Design, 1996, 118(2): 115-122.

[28] Delaurentis D A. A probabilistic approach to aircraft design emphasizing stability and control uncertainties [D]. Georgia Institute of Technology, 1998.

[29] Padmanabhan D. Reliability-based optimization for multidisciplinary system design [D]. Aerospace and Mechanical Engineering Notre Dame, 2003.

[30] 刘宝碇, 彭锦. 不确定性理论教程[M]. 北京: 清华大学出版社, 2005.

[31] Klir G J. Uncertainty and information measures for imprecise probabilities:an overview[C]. The 1st International Symposium on Imprecise Probabilities and Their Applications, Ghent, 1999.

[32] Walley P. Towards a unified theory of imprecise probability[J]. International Journal of Approximate Reasoning, 2000, 24(2-3): 125-148.

[33] Shafer G A. Mathematicaltheory of evidence[M]. Princeton: Princeton University Press, 1976.

[34] Yager R, Kacprzy K J, Fedrizzi M.Advances in the dempster-shafer theory of evidence[M]. New York: John Wiley and Sons, 1994.

[35] Mourelatos Z, Zhou J. A design optimization method using evidence theory[J]. Journal of Mechanical Design, 2006, 128(4): 901-908.

[36] Zadeh L A. Fuzzysets[J]. Information and Control, 1965, 8(3): 338-353.

[37] 杨伦标, 高英仪. 模糊数学原理及其应用[M]. 广州: 华南理工大学出版社, 2000.

[38] Zimmermann H J. Fuzzy Sets, Decision making, andexpert systems[M]. Boston: Kluwer Academic Publishers, 1987.

[39] Zadeh L A. Fuzzy sets as a basis for a theory of possibility[J]. Fuzzy Sets and Systems, 1978, 1(1): 3-28.

[40] Rao S S, Berke L. Analysis of uncertain structural systems using interval analysis[J]. AIAA Journal, 1997, 35(4): 727-735.

[41] Rao S S, Lingtao C. Optimum design of mechanical systems involving interval parameters[J]. Journal of mechanical Design, 2002, 124(3): 465-472.

[42] Majumder L, Rao S S. Interval-based multi-objective optimization of aircraft wings under gust loads[J]. AIAA Journal, 2009, 47(3): 563-575.

[43] Moore R E, Kearfott R B, Cloud M J. Introduction tointerval analysis[M]. Philadelphia: SIAM Press, 2009.

[44] Ben-Haim Y, Elishakoff I. Convex models of uncertainty in applied mechanics [M]. Amsterdam: Elsevier, 1990.

[45] Wu Y T, Enright M P, Millwater H R, et al. Probabilistic methods for design assessment of reliability with inspection [C]. The 41st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference and Exhibit, Atlanta, 2000.

[46] Bae H R, Grandi R V, Canfield R A. Uncertainty quantification of structural response using evidencetheory [R]. AIAA 2002-1468, 2002.

[47] Harish A, John E R, Evan L P, et al. Uncertainty quantification using evidence theory in multidisciplinary design optimization [J]. Reliability Engineering and System Safety, 2004, 85: 281-294.

[48] Saltelli A, Ratto M, Andres T, et al.Global sensitivity analysis: the primer [M]. Chichester: John Wiley and Sons, 2008.

[49] Helton J C, Johnson J D, Salaberry C J, et al. Survey of sampling-based methods for uncertainty and sensitivity analysis [J]. Reliability Engineering and System Safety, 2006, 91(10-11): 1175-1209.

[50] Iman R L, Helton J C. An investigation of uncertainty and sensitivity analysis techniques for computer models [J]. Risk Anal, 1988, 8(1): 71-90.

[51] Mihaela I B, Dan G C. A comparative review of sensitivity and uncertainty analysis of large-scale systems I: deterministic methods[J]. Nuclear Science and Engineering, 2004, 147(3): 139-203.

[52] Dan G C, Mihaela I B. A comparative review of sensitivity and uncertainty analysis of large-scale systems II: statistical methods [J]. Nuclear Science and Engineering, 2004, 147(3): 204-217.

[53] Liu H, Chen W, Sudjianto A. Probabilistic sensitivity analysis methods for design under uncertainty [C]. The 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Albany, 2004.

[54] Hofer E. Sensitivity analysis in the context of uncertainty analysis for computationally intensive models [J]. Computer Physics Communications, 1999, 117(1-2): 21-34.

[55] Helton J C, Johnson J D, Oberkampf W L, et al. Sensitivity analysis in conjunction with evidence theory representations of epistemic uncertainty [J]. Reliability Engineering and System Safety, 2006, 91(10-11): 1414-1434.

[56] Oberguggenberger M, King J, Schmelzer B. Classical and imprecise probability methods for sensitivity analysis in engineering: a case study [J]. International Journal of Approximate Reasoning, 2009, 50(4): 680-693.

[57] Bae H R, Grandhi R V, Canfield R A. Sensitivity analysis of structural response uncertainty propagation using evidence theory [J]. Structural and Multidisciplinary Optimization, 2006, 31(4): 270-291.

[58] Guo J, Du X. Sensitivity analysis with mixture of epistemic and aleatory uncertainties [J]. AIAA Journal, 2007, 45(9), 2337-2349.

[59] Guo J. Uncertainty analysis and sensitivity analysis for multidisciplinary system design [D]. Rolla: Missouri University of Science and Technology, 2008.

[60] Keane A J, Nair P B. Computational approaches for aerospace design: the pursuit of excellence [M]. Chichester: John Wiley and Sons, 2005.

[61] Wiener N. Thehomogeneous chaos [J]. American Journal of Mathematics, 1938, 60(4): 897-936.

[62] Loïc B, Mathieu B, Nicolas B, et al. Decoupled multidisciplinary design optimization formulation for interdisciplinary coupling satisfaction under uncertainty [J]. AIAA Joirnal, 2016, 54(1): 186-205.

[63] Ghanem R, Spanos P. Stochastic finite elements: a spectral approach [M]. New York: Springer-Verlag, 1991.

[64] Le Maitre O P, Knio O M, Najm H N, et al.A stochastic projection method for fluid flow I. basic formulation [J]. Journal of Computational Physics, 2001, 173(2): 481-511.

[65] Le Maitre O P, Reagan M T, Najm H N, et al.A stochastic projection method for fluid flow II. random process [J]. Journal of Computational Physics, 2002, 181(1): 9-44.

[66] 宋军，吕震宙，袁修开. 相关情况下可靠性灵敏度分析的矩方法[J]. 计算力学学报, 2009, 26(2): 215-220. [Song Jun, Lu Zhen-zhou, Yuan Xiu-kai. Reliability sensitivity for correlative variables by moment method[J]. Chinese Journal of Computational Mechanics, 2009, 26(2): 215-220.]

[67] Ghosh S, Lee C H, Mavris N D. Covariance matching collaborative optimization for uncertainty-based multidisciplinary aircraft design [C]. 15th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Atlanta, GA, 2014.

[68] Jiang Z, Chen W, German J B. Statistical sensitivity analysis considering both aleatory and epistemic uncertainties in multidisciplinary design [C]. 15th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Atlanta, GA, 2014.

[69] Chen L, Sankaran M. Stochastic multidisciplinary analysis with high-dimensional coupling [J]. AIAA JOURNAL, 2016, 54(4): 1209-1219.

[70] Du X, Chen W.An efficient approach to probabilistic uncertainty analysis in simulation-based multidisciplinary design [C]. The 38th AIAA Aerospace Science Meeting and Exhibit, Reno, 2000.

[71] Du X, Chen W. efficient uncertainty analysis methods for multidisciplinary robust design [J]. AIAA Journal, 2002, 40(3): 545-552.

[72] Du X, Wang Y, Chen W.Methods for robust multidisciplinary design [C]. The 41st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference and Exhibit, Atlanta, 2000.

[73] Gu X，Renaud J E，Penninger C L. Implicit uncertainty propagation for robust collaborative optimization [C]. Proceedings of Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Pittsburgh, 2001.

[74] Ghosh S, Mavris N D. A methodology for probabilistic analysis of distributed multidisciplinary architecture (PADMA) [C]. 17th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Washington, D.C., 2016.

[75] Liu D, Choi K K. An inverse analysis method for design optimization with both statistical and fuzzy uncertainties [J]. Structural and Multidisciplinary Optimization, 2006, 37(2): 107-119.

[76] Adduri P R, Penmetsa R C.System reliability analysis for mixed uncertain variables [J]. Structural Safety, 2009, 31(5): 375-382.

[77] Zhang X, Huang H, Xu H.Multidisciplinary design optimization with discrete and continuous variables of various uncertainties [J]. Structural and Multidisciplinary Optimization, 2010, 42(4): 605-618.

[78] Du X.Unified uncertainty analysis by the first order reliability method [J]. Journal of Mechanical Design, 2008, 130(9): 1404-1404.

[79] Eldred M S, Swiler L P, Tang G.Mixed aleatory-epistemic uncertainty quantification with stochastic expansions and optimization-based interval estimation [J]. Reliability Engineering and System Safety, 2011, 96(9): 1092-1113.

[80] 陈立周. 稳健设计[M]. 北京: 机械工业出版社, 2000.

[81] Park S H. Robust design and analysis for quality engineering [M]. London: Chapman and Hall, 1996.

[82] Park G J, Lee T H, Lee K H, et al.Robust design: an overview [J]. AIAA Journal, 2006, 44(1): 181-191.

[83] Beyer H G, Sendhoff B. Robust optimization: a comprehensive survey [J]. Computer Methods in Applied Mechanics and Engineering, 2007, 196(33-34): 3190-3218.

[84] Mohan N S. Robustdesign [D]. Bombay: Indian Institute of Technology, 2002.

[85] Taguchi G, Elsayed E A, Hsiang T C. Quality engineering in production systems [M]. New York: McGraw-Hill, 1989.

[86] Lee K, Park G J.Robust optimization considering tolerances of design variables [J]. Computers and Structures, 2001, 79(1): 77-86.

[87] Rai M M. Robust optimal design with differential evolution [C]. The 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Albany, 2004.

[88] Li M, Azarm S, Aute V. A multi-objective genetic algorithm for robust design optimization [C]. Proceedings of the 7th annual conference on Genetic and evolutionary computation, Washington DC, 2005.

[89] Chen W, Sahai A, Messac A, et al. Exploration of the effectiveness of physical programming in robust design [J]. Journal of Mechanical Design, 2000, 122(2): 155-163.

[90] Messac A, Ismail-Yahaya A. Multi-objective robust design using physical programming [J]. Structural and Multidisciplinary Optimization, 2002, 23(5): 357-371.

[91] Chen W, Wiecek M M, Zhang J. Quality utility: a compromise programming approach to robust design [J]. Journal of Mechanical Design, 1999, 121(2): 179-187.

[92] Govindaluri S M, Cho B R. Robust design modeling with correlated quality characteristics using a multicriteria decision framework [J]. International Journal of Advanced Manufacturing Technology, 2007, 32(5-6): 423-433.

[93] Freudenthal A M.Civil engineering classics[M]. New York: American Society of Civil Engineers, 2015.

[94] Coenell C A. A probability-based structural code [J]. Journal of the American Concrete Institute, 1969, 66(12): 974-985.

[95] Sundaresan S, Ishii K, Houser D R. A robust optimization procedure with variations on design variables and constraints [J]. Engineering Optimization, 1995, 24(24): 101-117.

[96] Parkinson A, Sorensen C, Pourhassan N. A general approach for robust optimal design [J]. Journal of Mechanical Design, 1993, 115(1): 74-80.

[97] Cheng G, Xu L, Jiang L. A sequential approximate programming strategy for reliability-based structural optimization [J]. Computers and Structures, 2006, 84(21): 1353-1367

[98] Du X, Chen W. Towards a better understanding of modeling feasibility robustness in engineering design [J]. Journal of Mechanical Design, 2000, 122(4): 385-394.

[99] Kuran B. Reliability based design optimization of a solid rocket motor using surrogate models [C]. The 43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Cincinnati OH, 2007.

[100] Po T L, Hae C G. Reliability-based multidisciplinary design optimization using probabilistic gradient-based transformation method [J]. Journal of Mechanical Design, 2013, 135(2): 137-145.

[101] Wu Y T, Shin Y, Sues R, et al. Safety-factor based approach for probability-based design optimization [C]. The 42nd Structures, Structural Dynamics, and Materials Conference and Exhibit, Seattle, 2001.

[102] Du X, Chen W. Sequential optimization and reliability assessment method for efficient probabilistic design [C]. Proceedings of ASME Design Engineering Technical Conference and Computers and Information in Engineering Conference, Montreal, 2002.

[103] Chen X G, Hasselman T K, Neill D J. Reliability-based structural design optimization for practical applications [C]. The 38th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 1997.

[104] Harish A, John R, Jason L, et al. A unilevel method for reliability based design optimization [C]. The 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Palm Springs, California, 2004.

[105] Mcallister C D, Simpson T W.Multidisciplinary robust design optimization of an internal combustion engine [J]. Journal of Mechanical Design, 2003, 125(1): 39-41.

[106] Padmanabhan D, Batill S.Reliability based optimization using approximations with applications to multi-disciplinary system design [C].The 40th AIAA Aerospace Sciences Meeting and Exhibit, Reno, 2002.

[107] 苏子健. 多学科设计优化的分解、协同及不确定性研究[D]. 武汉: 华中科技大学, 2008. [Su zi-jian. Research on the decomposition, coordination and uncertainty of the multidisciplinary design optimization[D]. Wuhan: Huazhong University of Science and Technology, 2008.]

[108] 许林. 飞行器MDO过程及相关技术研究与应用[D]. 长沙: 国防科学技术大学, 2009. [Xu lin. Research and application of aerospace vehicle MDO process and related technologies[D]. Changsha: National University of Defense Technology, 2009.]

[109] Kokkolaras M, Mourelatos Z P, Papalambros P Y. Design optimization of hierarchically decomposed multilevel systems under uncertainty [J]. Journal of Mechanical Design, 2006, 128(2): 503-508

[110] Liu H, Chen W, Kokkolaras M, et al.Probabilistic analytical target cascading: a moment matching formulation for multilevel optimization under uncertainty [J]. Journal of Mechanical Design, 2006, 128(4): 1173-1182.

[111] Xiong F, Yin X, Chen W, et al.Enhanced probabilistic analytical target cascading with application to multi-scale design [J]. Engineering Optimization, 2010, 42(42): 581-5

[112] Delaurentis D A. A probabilistic approach to aircraft design emphasizing stability and control uncertainties [D]. Georgia Institute of Technology, 1998.

[113] Chen W, Lewis K. A robust design approach for achieving flexibility in multidisciplinary design [J]. AIAA Journal, 1999, 37(8): 982-990.

[114] Aminpour M A, Shin Y, Sues R H, et al. A framework for reliability-basedMDO of aerospace systems [C]. The 43rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference and Exhibit, Denver, 2002.