空间光谱干涉仪在轨超静超稳平台的设计与地面验证
段鹏飞,关 新,郑钢铁,钟 鸣,欧宗耀,于宗伟,邵益凯
(1.北京空间机电研究所,北京 100094;2.清华大学航天航空学院,北京 100190;3.北京控制工程研究所,北京 100190;4.上海卫星工程研究所,上海 201109)
0 引 言
随着科学和业务任务的发展,卫星本体及其所携带的有效载荷结构越来越复杂,无法人为控制的外部环境和复杂的内部环境,使卫星系统在轨长期处于微振动状态。同时随着空间技术的发展,对振动环境有着高精度要求的高灵敏度空间光学载荷逐渐增多,主要包括长焦距、大口径、高指向精度的高空间分辨率成像载荷,以及高运动稳定性要求的干涉仪型高光谱分辨率探测载荷等。卫星微振动会导致成像载荷指向精度的下降和图像的模糊;对于干涉仪型光谱探测载荷,微振动则会引起机构运动精度的下降,导致载荷性能不达标。因此,解决在轨微振动影响的超静超稳平台技术已经成为高灵敏度光学载荷的关键技术之一[1-3]。
从公开的文献来看,针对空间光学载荷的振动控制技术发展最早的是美国NASA,典型案例是2002年哈勃太空望远镜太阳帆板的阻尼减振器[4]。同一时期,依托成熟的主被动结合式振动控制技术,美国CSA,Honeywell等科研单位研制出面向空间光学载荷的超静超稳平台[5-6],并通过飞行试验或地面试验进行了有效性的验证,包括2006年发射的战术小卫星Tacsat-2[7],2008年发射的GeoEye-1卫星[8],2009年发射的WorldView-2卫星[9],太阳系外行星探测计划ACCESS[10],以及计划于2018年发射的詹姆斯·韦伯太空望远镜JWST[11]等。近十余年我国空间振动控制技术进步显著,国内高校,中科院以及航天科研院所通过产、学、研的协作方式,发展了遥感卫星动力学问题的关键技术,发现并不断克服在轨振动控制产品研制过程中的设计和工艺问题,已逐步建成微振动问题的产品线,并在型号中实现了应用[12-17]。
然而目前国内外在轨微振动控制主要针对高空间分辨率的成像载荷,针对干涉仪型高光谱分辨率探测载荷的暂无公开报道。本论文以某空间光谱干涉仪型号为背景,系统研究了干涉仪的微振动隔振设计以及地面试验验证。
1 在轨减振任务特点
我国某气象卫星上搭载了一台干涉仪型光谱探测光学载荷,其结构布局和干涉仪结构如图1所示。
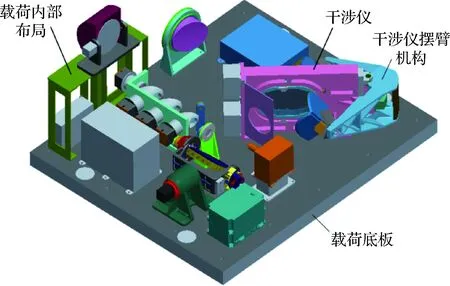
图1 载荷内部结构布局及干涉仪Fig.1 The Interferometer and the layout of the payload
根据任务需求,干涉仪摆臂机构需要保持极高的速度稳定度,偏差应低至1%以内,这在结构上要求干涉仪安装位置的加速度时域峰峰值不超过1.0×10-2gn,20 Hz~500 Hz频域范围内不超过0.35×10-2gn[18]。然而卫星上的飞轮以及周边载荷的扫描机构、机械制冷机等多个振动源会影响干涉仪的速度稳定性。卫星微振动试验表明,载荷安装位置加速度时域峰峰值约2.4×10-2gn,20 Hz~500 Hz频域加速度幅值1.4×10-2gn,显著超出了干涉仪的承受范围,需要通过减振手段来保证干涉仪的在轨力学环境。
从外部环境加速度频域幅值来看,扰动能量大量分布在中、高频段,而干涉仪对于采样时间内自身结构的正弦运动比直线运动更为敏感,即高频振动对干涉仪速度稳定性的影响更大。从动力学的角度,柔性低连接刚度的方法能够有效隔离中、高频段扰动能量的传递,适合干涉仪减振的需要。
从载荷的结构形式来看,微振动敏感的干涉仪是光学系统的一部分,仅针对干涉仪隔振容易导致干涉仪偏离系统光路,因此需要考虑对整体光学载荷进行隔振,这就大大增加了减振设计的难度:载荷整机相对于干涉仪惯性大且特性复杂,而柔性隔振减弱连接刚度,会导致载荷相对于卫星结构产生低频共振,以及在卫星发生调姿等较大幅度的动作后,载荷相对于卫星结构持续的低频晃动,这样的共振和晃动不但会影响载荷探测任务的稳定,还将严重影响卫星在轨姿态的稳定和结构的安全。
为了克服上述问题,需要一套新型的减振思路,在保证干涉仪摆臂机构速度稳定度的过程中,不能使其光路偏离光学系统,同时要保证载荷与卫星结构的机动保持一致,无相对晃动。
2 在轨超静超稳平台设计
2.1 减振总体方案
根据在轨减振任务特点的分析,为了保证干涉仪不会偏离光学系统光路,减振环节需要在载荷与卫星的连接位置之间引入;采用低刚度连接隔振的方法隔离来自平台的中、高频的振动能量;并采用高灵敏度阻尼的方法克服低刚度连接带来的载荷低频共振和晃动。空间光谱干涉仪在轨超静超稳平台包括隔振器和阻尼器,如图2所示。
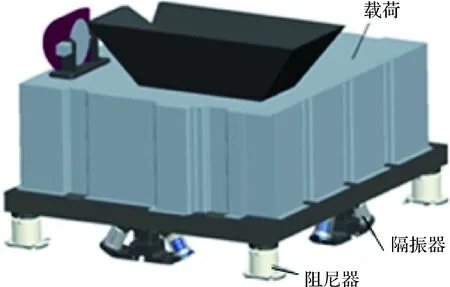
图2 干涉仪减振方案Fig.2 Scheme on the vibration attenuation
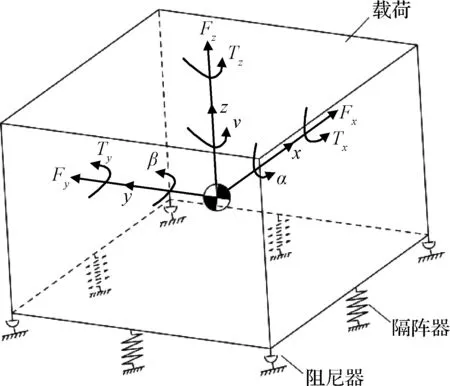
图3 载荷减振力学模型Fig.3 Dynamic model on the payload vibration attenuation
经模态测试验证,探测光学载荷模态频率大于100 Hz,相对于低刚度的隔振器可近似作为刚体。载荷减振模型简化后得到的力学模型如图3所示。其中,x,y,z分别代表载荷纵向,横向,垂向的往复位移,α,β,ν分别代表横摇,纵摇,旋转的回转角。Fx,Fy,Fz分别表示作用在载荷质心的激励力,Tx,Ty,Tz分别表示外部激励力矩。
载荷引入超静超稳平台前的控制方程为
(1)
引入后所组成的隔振系统模型的控制方程为
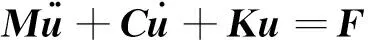
(2)
其中,M表示载荷的质量矩阵,
(3)
K表示隔振器的总刚度矩阵,
(4)
C表示阻尼器的阻尼矩阵,
(5)
u(0),u表示载荷质心处的广义位移列矢量,u(0)表示超静超稳平台引入前的,u表示引入后的,
(6)
F则是作用在载荷质心的激励力列矢量,
F=[FxFyFzTxTyTz]
(7)
式(7)中,m为载荷的总质量;Jxx,Jyy,Jzz为载荷绕主坐标轴的转动惯量;Jmn(m≠n)为载荷相对于主坐标轴的质量惯性积,Jmn=Jnm(m≠n)。Kxx,Kyy,Kzz为隔振器的总往复刚度;Kαα,Kββ,Kνν为隔振器的总回转刚度;Kmn=Knm(m≠n)为隔振器的各种耦合刚度。Cxx,Cyy,Czz为阻尼器的总往复阻尼值;Cαα,Cββ,Cνν为阻尼器的总回转阻尼值;Cmn=Cnm(m≠n)为阻尼器的各种耦合阻尼值。
利用式(3),式(4)和式(6),求解式(2)广义特征值问题,得到表征载荷与超静超稳平台所组成的隔振系统的模态特征值λm与特征向量φm(m=1,2,…,6)。假设系统没有重根,则按照由小至大的顺序将各个根排列起来,有
λ1<λ2<…<λ6
(8)
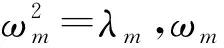
定义阵型矩阵
Φ=[φ1φ2…φ6]
(9)
使用坐标变换
u=Φq
(10)
则q为隔振系统的模态坐标向量。利用式(9),式(10)将控制方程式(2)变换至模态坐标下,有
(11)
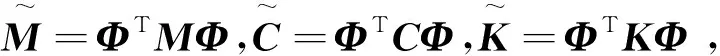
(12)
(13)
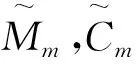
(14)
隔振系统第m阶临界阻尼比ζm为
(15)
式(14),式(15)与单自由度隔振系统隔振频率和临界阻尼比表达形式完全相同。
对式(1)做Laplace变换可得超静超稳平台引入前卫星扰振力至载荷广义位移的第m阶传递函数
(16)
对式(11)做Laplace变换,考虑式(12)和式(13),求解式(11)相当于6个独立的单自由度系统作强迫振动,可得超静超稳平台引入后卫星扰振力至载荷广义位移的第m阶振动传递率
m=1,2,…,6
(17)
对于相同的扰振力F,将式(16)和式(17)相除可以得到超静超稳平台引入前、后载荷位移响应的关系,用于评价减振效果
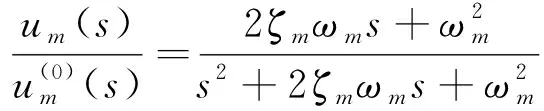
(18)
结果亦与单自由度隔振系统振动传递率表达形式相同。
在式(18)中令s=iω,可得减振效果的幅频特性表达式
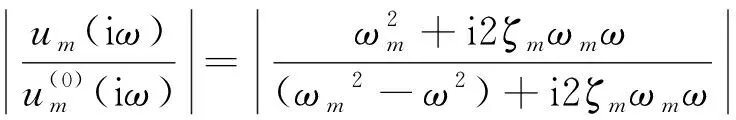
(19)
式中:ω为来自卫星扰振力的频率。
实际工程实现过程中,临界阻尼比ζ一般在0.05~0.5之间,不同ζ的幅频特性曲线如图3所示。
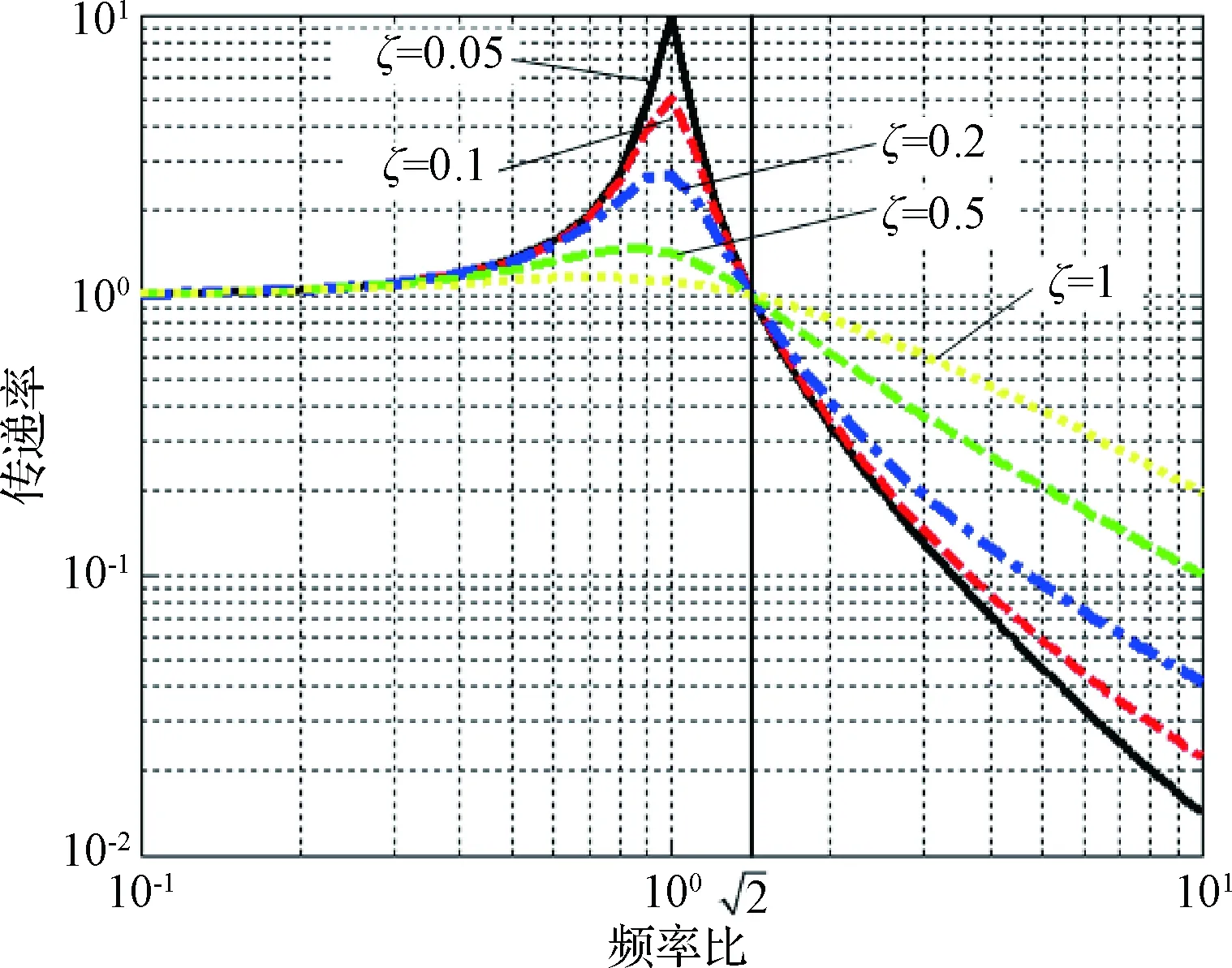
图4 减振效果幅频曲线Fig.4 Transmissibility of vibration attenuation
2.2 干涉仪超静超稳平台设计
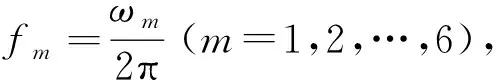
从表1可以看出,隔振频率小于5 Hz时可以实现主要扰动频率位置高于60%的衰减率,能够满足任务减振需求。
计算一阶隔振频率f1从0.5 Hz到9 Hz时载荷的晃动角,得到图5所示曲线。由图5可知,随着隔振频率的上升,晃动角先减小后上升,在3 Hz到6 Hz之间存在一个低谷。这表明在较低隔振频率时,增加隔振器刚度,在同样的力矩作用下,晃动角幅值减小。但当一阶隔振频率f1增大至接近激励频率时,晃动幅值急剧上升,向共振状态接近。综上本方案一阶隔振频率f1取5 Hz。
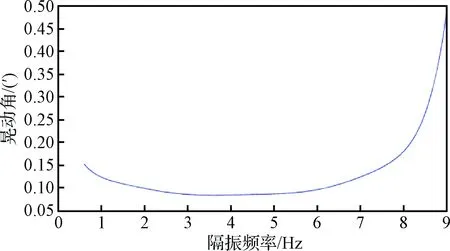
图5 不同一阶隔振频率载荷晃动角计算结果Fig.5 Angle amplitude vs. isolation frequency
隔振器结构设计的关键是隔振弹簧,其低刚度的镂空结构决定了超静超稳平台的隔振频率。其它组成结构还包括分别与载荷和卫星舱板连接的上、下转接座,以及防止在轨倾覆的限位装置。产品组成如图6所示。
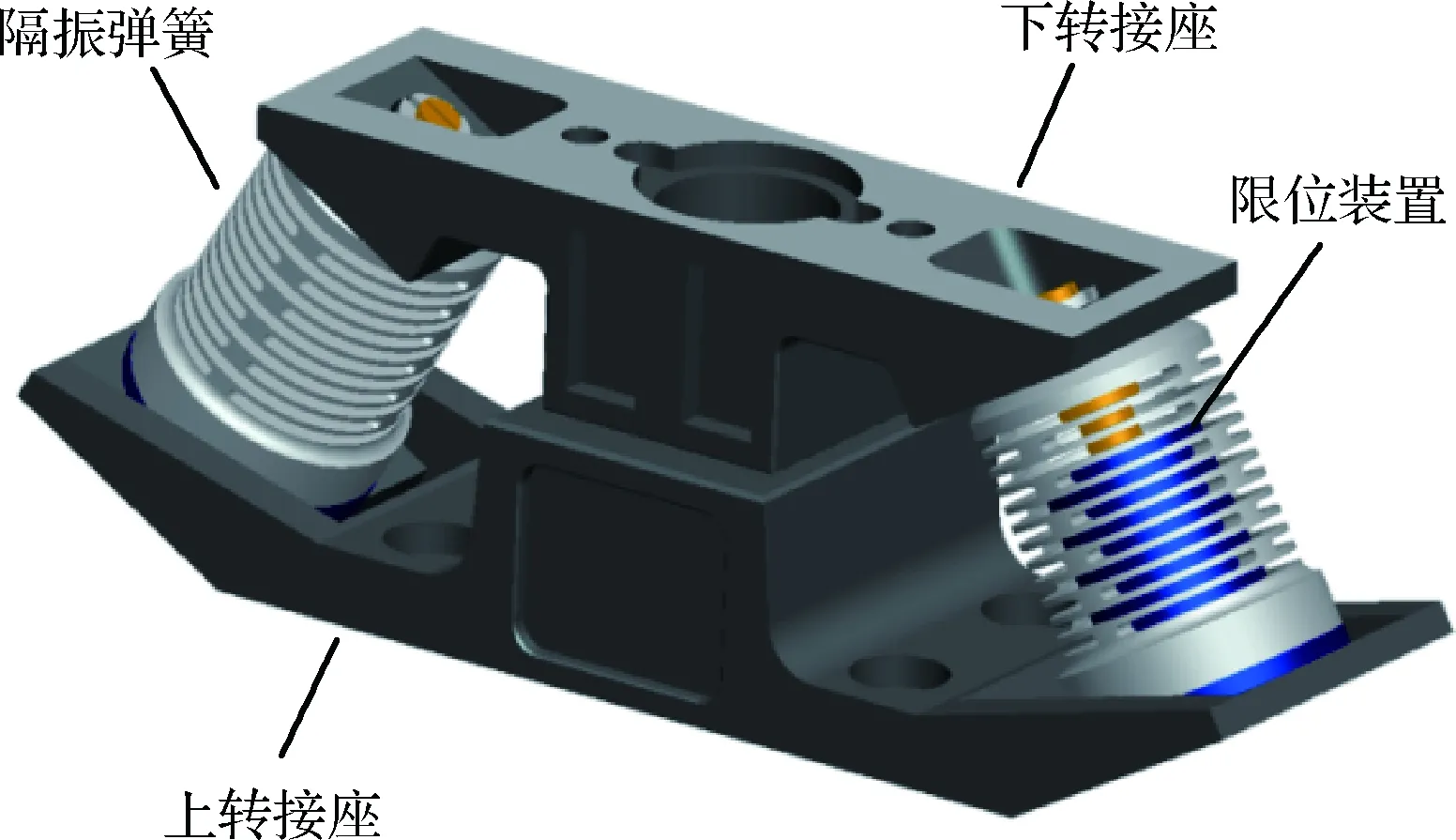
图6 隔振器结构组成Fig.6 Structure of the isolator
阻尼器提供阻尼力,其作用只与卫星和载荷间的相对速度有关。核心是临界阻尼比ζm(m=1,2,…,6)。由图4可知,高ζ值会显著抑制低频共振,但会影响中高频的减振效率,反之效果相反。
阻尼值的选取在保证隔振器低频引入的以及星上各振动源传递来的振动幅值都要低于干涉仪所能够承受的,同时还需要保证有足够的阻尼力与隔振器提供的恢复力共同克服载荷相对卫星极端情况晃动的惯性力。表2给出了阻尼器取不同阻尼值时载荷的一阶模态阻尼比及瞬态晃动衰减时间,其中一阶频率取5 Hz,经过优化和权衡,本方案阻尼器临界阻尼比ζ取值0.2。
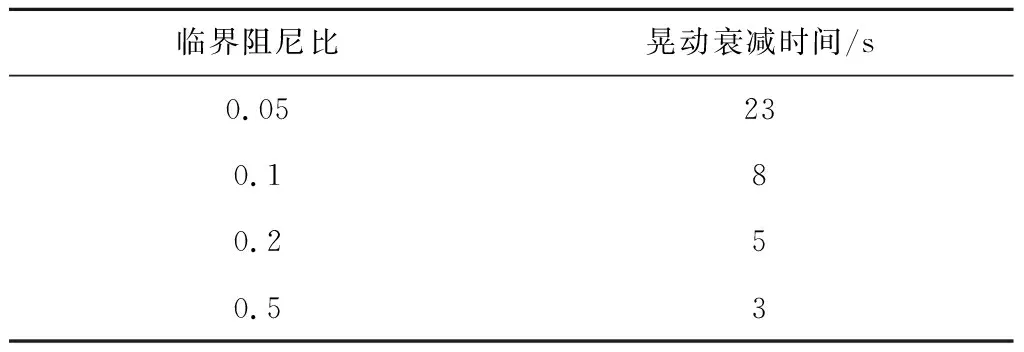
表2 临界阻尼比对晃动时间影响Table 2 Shaking time with different critical damp ratios
阻尼器结构为基于楞次定理的电磁阻尼器[19],由作用导电体组件、永磁体组件及磁密封壳组成,其结构形式如图7所示。作用导电体组件的导体为铜合金材料,永磁体为稀土永磁材料。作用导电体组件与载荷连接,永磁体组件则与卫星结构固定,当载荷与星体结构发生相对运动时,导体在永磁体产生的磁场中运动,导体内形成电涡流从而产生阻尼力,将相对运动的机械能转换为内能。作用导电体组件与永磁体组件、磁密封壳之间在各方向均设计有足够的间隙,相对运动过程中不会发生接触,不存在冷焊或卡死的问题。超静超稳平台总阻尼值C约1500 N· s/m,平台有4个阻尼器,每个阻尼器阻尼值设计为375 N·s/m。此外为了减小永磁体对星体姿态等的影响,采用软铁材料制成密封壳以实现磁密封。
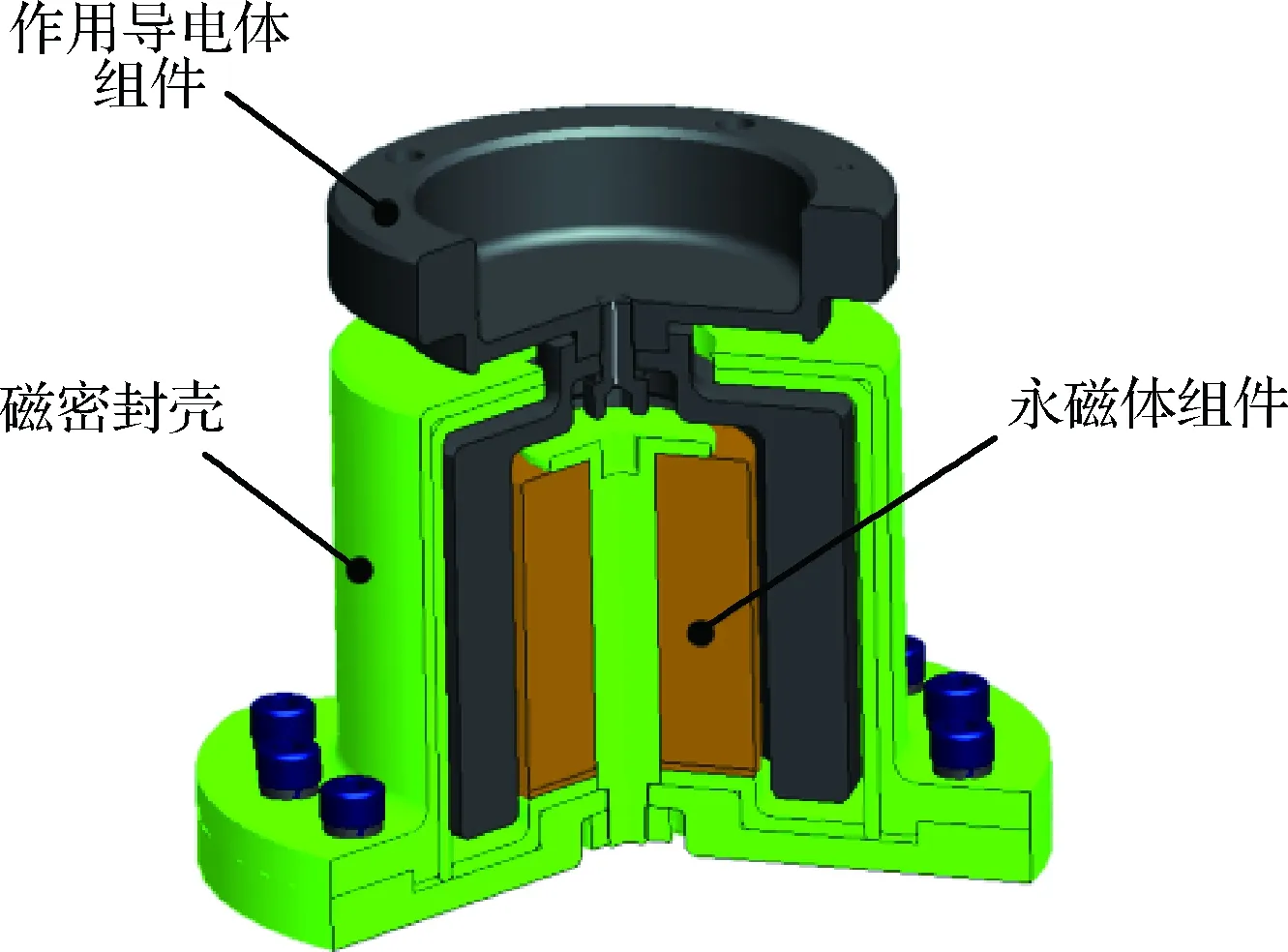
图7 电磁阻尼器结构Fig.7 Structure of electromagnetism damping
相比于传统的粘滞或粘弹性阻尼器,电磁阻尼器有更高的结构相对运动速度灵敏度,且不含流体或橡胶材料,没有在轨泄漏与挥发物污染的风险。
2.3 减振性能预估
对超静超稳平台引入后载荷结构的动力学特征,及其在中高频段减振效率进行预估。超静超稳平台与载荷结构的模态及特征频率见图8。
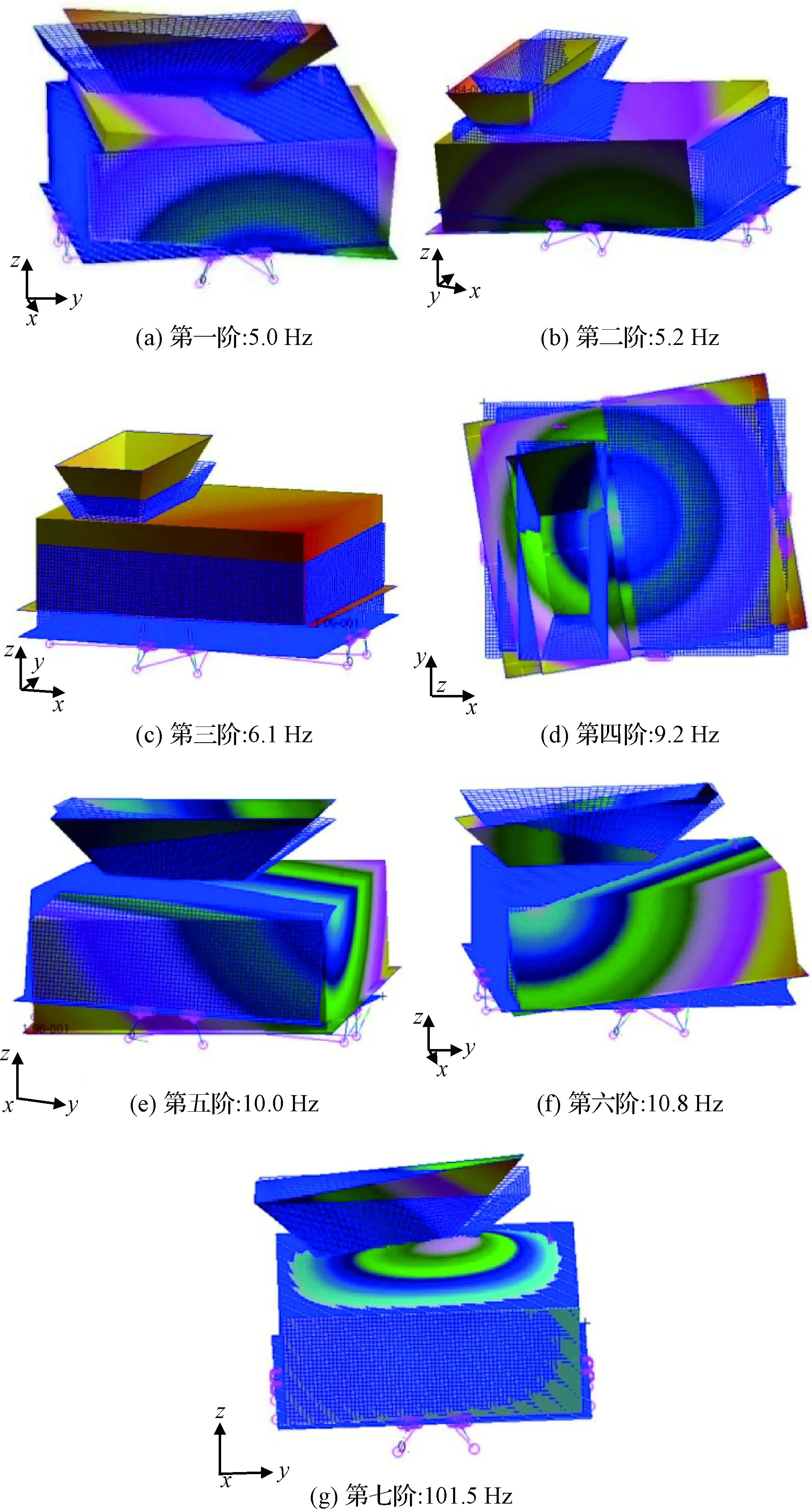
图8 隔振系统模态频率Fig.8 Mode frequencies of the isolation system
系统前六阶频率集中在5 Hz~11 Hz,模态表现为载荷的刚体模态特征。第七阶模态频率101.5 Hz,模态为载荷自身结构特征。由此可以判定5 Hz为隔振系统的一阶隔振频率,隔振频率带宽约6 Hz。
以超静超稳平台底端安装面为输入,以干涉仪安装位置为输出,计算六自由度结构传递率。计算结果见图9。从图9可以看出,在13 Hz之后测点位置各自由度传递率<1,即超静超稳平台从13 Hz左右开始具有隔振效果;在100 Hz处可以实现约97%的传递率衰减。
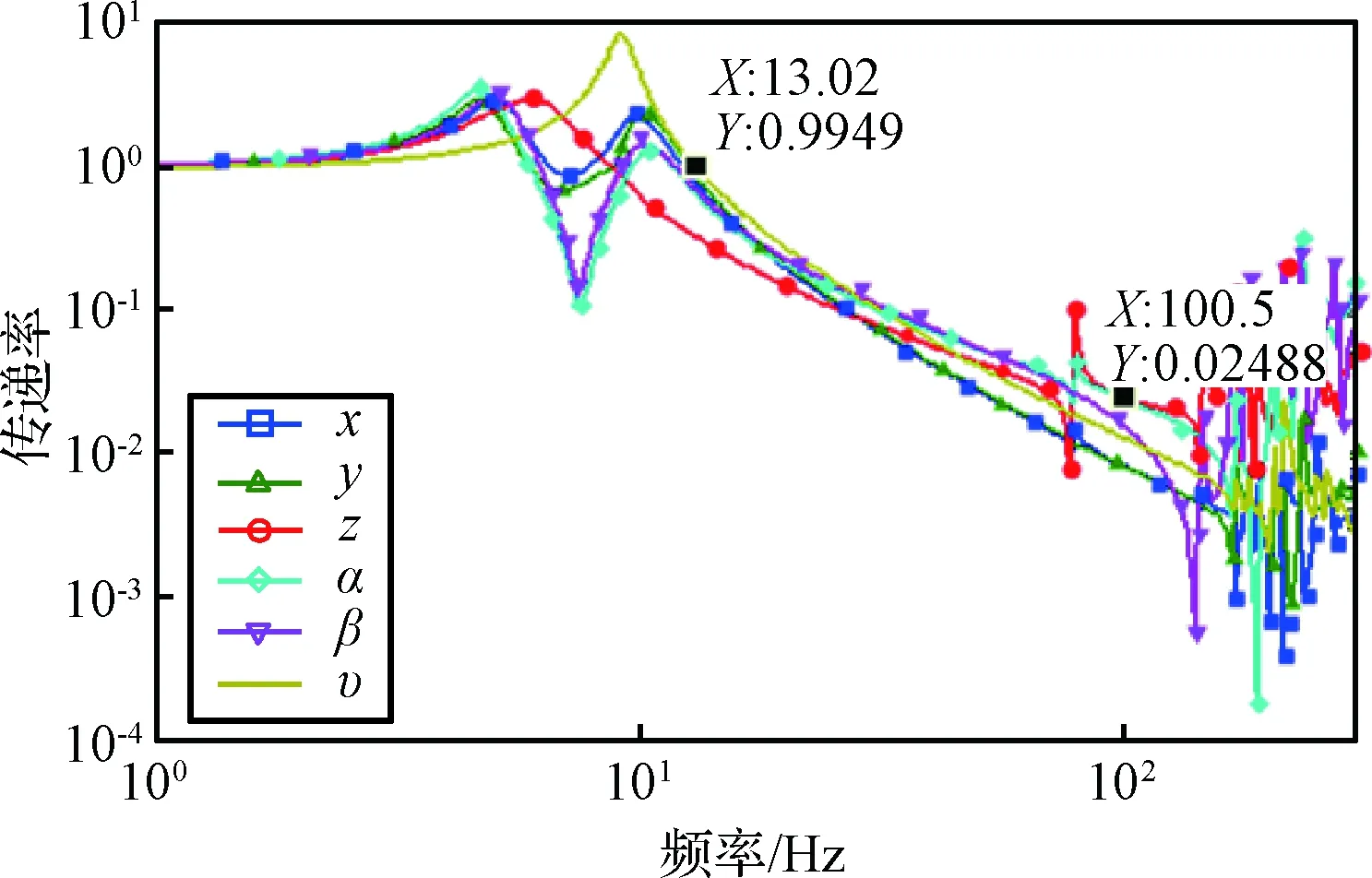
图9 隔振系统六自由度传递率Fig.9 Transmissibility of the isolation in 6 DOF
图10对载荷在轨减振的设计思路给出了建议:首先结合载荷自身特点进行微振动影响的敏感性分析,得到载荷微振动的敏感度,同时进行卫星平台振源特性的测试和分析,然后在此基础上利用减振理论和方法开展在轨减振方案设计和产品研制,针对性地解决微振动带来的影响,并在地面进行必要的专项验证试验。
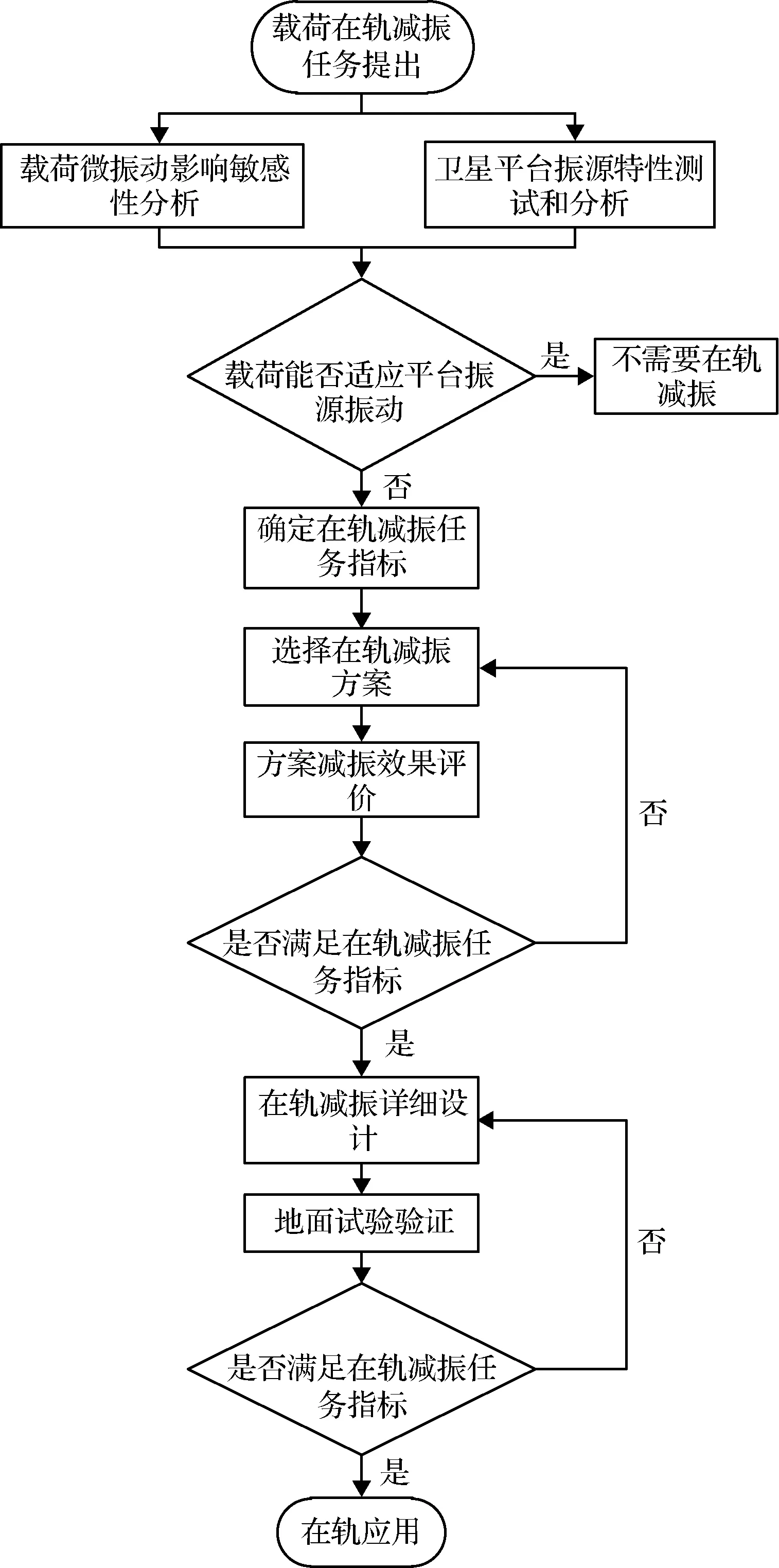
图10 在轨减振工程实现流程图Fig.10 The flowchart of in-orbit vibration attenuation
3 地面试验验证
超静超稳平台研制完成后,需要在地面对其功能和性能进行全面和充分的试验验证。卫星微振动试验能够得到实际星上扰动条件下超静超稳平台的性能,是地面最接近在轨实际的考核。试验过程如图11所示,卫星结构通过弹簧悬吊,其重力被弹簧拉力所平衡,同时弹簧刚度很低,结构悬吊频率约0.15 Hz,这有效地模拟了结构在轨失重的悬浮状态。卸载支撑在保证不施加附加约束而影响悬浮效果的同时,提供卫星结构必要的安全限位。微振动测试时,为了保证超静超稳平台处于无外力约束的自由状态,载荷也通过弹簧悬吊。
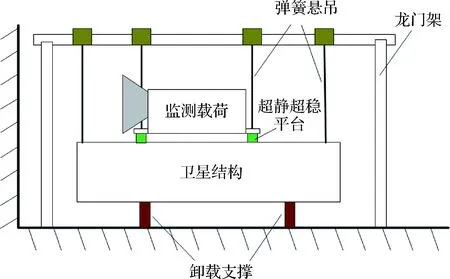
图11 卫星微振动试验布局Fig.11 The layout of the micro-vibration test
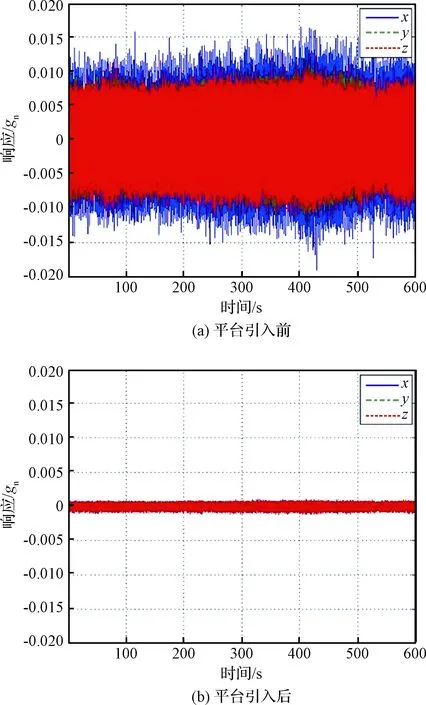
图12 整星微振动试验干涉仪安装位置时域加速度响应Fig.12 The interferometer response in time-area during the satellite micro-vibration test
干涉仪安装位置处时域加速度峰峰值响应情况:超静超稳平台引入前约2.4×10-2gn,引入后约0.2×10-2gn,减振效率约92%。曲线如图12所示。全频域最大响应幅值情况:超静超稳平台引入前约0.93×10-2gn,引入后约0.045×10-2gn,减振效率约95.2%。曲线如图13所示。超静超稳平台引入后,干涉仪性能稳定,载荷工作正常。
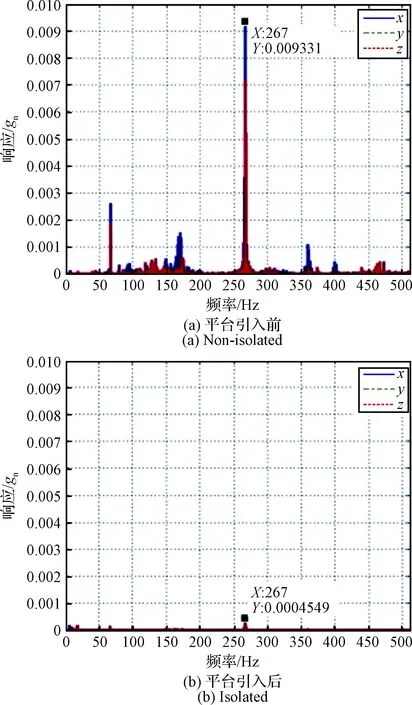
图13 整星微振动试验干涉仪安装位置频域加速度响应Fig.13 The interferometer response in frequency-area during the satellite micro-vibration test
4 结 论
在轨微振动对高灵敏度载荷有很大影响。本文根据我国某气象卫星上一台高灵敏度干涉仪在轨工作的特点,针对性地设计了一套能够隔离星上微振动影响,保证干涉仪在轨工作环境的超静超稳平台。地面卫星微振动试验时,超静超稳平台启动后保证了干涉仪的正常工作,很好地满足了任务要求。
参 考 文 献
[1] 徐广德, 武江凯, 苟仲秋, 等. 国外航天器高精度高稳定度高敏捷指向技术综述[J]. 航天器工程, 2017, 26(1): 91-99. [Xu Guang-de, Wu Jiang-kai, Gou Zhong-qiu, et al. High accuracy high stability and high agility pointing technology of spacecraft [J]. Spacecraft Engineering, 2017, 26(1): 91-99.]
[2] 谭天乐, 朱春艳, 朱东方, 等. 航天器微振动测试、隔离、抑制技术综述[J]. 上海航天, 2014, 31(6): 36-45. [Tan Tian-le, Zhu Chun-yan, Zhu Dong-fang, et al. Overview of micro-vibration testing, isolation and suppression technology for spacecraft [J]. Aerospace Shanghai, 2014, 31(6):36-45.]
[3] Bingham G E, Cantwell G, Robinson R C, et al. Image stability requirements for a geosynchronous imagingfourier transform spec-trometer (GIFTS) [C]. Proceedings of SPIE 4151, Hyperspectral Remote Sensing of the Land and Atmosphere, February 8, 2001.
[4] Anandakrishnan S M, Connor C T, Lee S, et al. Hubble space telescope solar array damper for improving control system stability[C]. Aerospace Conference, Montana, USA, March 18-25, 2000.
[5] Anderson E H,Fumo J P, Erwin R S. Satellite ultraquiet isolation technology experiment (SUITE) [C]. Aerospace Conference, Montana, USA, March 18-25, 2000.
[6] Richard G C, Jeanne M S, Alok D, et a1.Vibration isolation and suppression system for precision payload in space [J]. Smart Materials and Structures, 1999, 8(6): 798-812.
[7] McMickell M B, Kreider T, Hansen E, et a1. Optical payload isolation using the miniature vibration isolation system[C]. Industrial and Commercial Applications of Smart Structures Technologies, San Diego, USA, March 19-20, 2007.
[8] Matthews G, Jr K H,Egerman R. A paradigm shift to enable more cost effective space science telescope missions in the upcoming decades[C]. Modeling, Systems Engineering, and Project Management for Astronomy IV, San Diego, USA, June 27-July 1, 2010.
[9] 范宁, 祖家国, 杨文涛, 等. WorldView系列卫星设计状态分析与启示[J]. 航天器环境工程, 2014, 33(3): 337-342. [Fan Ning, Zu Jia-guo, Yang Wen-tao, et al. The design of WorldView satellite and its demonstrative value [J]. Spacecraft Environment Engineering, 2014, 33(3): 337-342.]
[10] Brugarolas P, Alexander J, Trauger J, et a1. ACCESS pointing control system[C]. Space Telescopes and Instrumentation: Optical, Infrared, and Millimeter Wave, San Diego, USA, June 27-July 2, 2010.
[11] Mosier G E, Howard J M, Johnston J D,et a1. The role of integrated modeling in the design and verification of the James Webb space telescope[C]. Space Systems Engineering and Opti-cal Alignment Mechanisms, Denver, USA, August 4-6, 2004.
[12] 张庆君, 王光远, 郑钢铁. 光学遥感卫星微振动抑制方法及关键技术[J]. 宇航学报, 2015, 36(2): 125-132. [Zhang Qing-jun, Wang Guang-yuan, Zheng Gang-tie. Micro-vibration attenuation methods and key techniques for optical remote sensing satellite [J]. Journal of Astronautics, 2015, 36(2): 125-132.]
[13] 关新, 王光远, 梁鲁, 等. 空间相机低频隔振系统及试验验证[J]. 航天返回与遥感, 2011, 32(6): 53-61. [Guan Xin, Wang Guang-yuan, Liang Lu, et al. Experimental demonstration of a low frequency isolation system for high resolution optical payload [J]. Spacecraft Recovery and Remote Sensing, 2011, 32(6): 53-61.]
[14] 葛东明, 邹元杰. 高分辨率卫星结构-控制-光学一体化建模与微振动响应分析[J]. 航天器环境工程, 2013, 30(6): 586-590. [Ge Dong-ming, Zou Yuan-jie. Structure-control-optics integrated modeling and micro-vibration analysis for high resolution satellite [J]. Spacecraft Environment Engineering, 2013, 30(6): 586-590.]
[15] 刘明辉, 梁鲁, 白绍竣, 等. 阻尼柔性连接在卫星结构中的综合应用研究[J]. 宇航学报, 2009, 30(1): 293-298. [Liu Ming-hui, Liang Lu, Bai Shao-jun, et al. Research into the integrative application of damped flexible connector in spacecraft structures [J]. Journal of Astronautics, 2009, 30(1): 293-298.]
[16] 王晓雷, 杨庆俊, 郑钢铁. 整星主动隔振平台研究[J]. 宇航学报,2007,28(2):438-441. [Wang Xiao-lei, Yang Qing-jun, Zheng Gang-tie. Study of whole-satellite active vibration isolation platform [J]. Journal of Astronautics, 2007, 28(2):438-441.]
[17] 郑钢铁, 梁鲁, 王光远, 等. 遥感卫星动力学问题系统解决方法和装置[C]. 2011年小卫星技术交流会, 北京, 中国,2011年9月1日. [Zheng Gang-tie, Liang Lu, Wang Guang-yuan, et al. Solutions and devices on the dynamics of remote sensor satellite [C]. Conference on the Minisatellite Technology 2011, Beijing, China,September 1, 2011.]
[18] 段鹏飞, 李明, 徐彭梅. 微振动对干涉仪运动机构均匀性的影响分析[J]. 航天返回与遥感, 2013, 35(6): 44-50. [Duan Peng-fei, Li Ming, Xu Peng-mei. Influence on velocity uniformity of interferometer mechanism of micro-vibration [J]. Spacecraft Recovery and Remote Sensing, 2013, 35(6): 44-50.]
[19] Matsuzaki Y, Ishikubo D, Kamita T, et al.Vibration control system using electromagnetic forces [J]. Journal of Intelligent Material Systems and Structures, 1997, 8(9): 751-756.

