改进模拟退火算法的喷管动力学模型修正

杜大华，贺尔铭，李 磊

(1. 西北工业大学航空学院，西安 710072；2. 液体火箭发动机技术国防科技重点实验室，西安 710100；3. 西北工业大学力学与土木建筑学院，西安 710072)

0 引 言

伴随着越来越恶劣的动力学服役环境，大型复杂装备结构的动力学问题愈来愈突出，对其动力学分析的建模精度要求不断提高，而进行动力学模型修正是提高其精度的重要环节[1-2]。然而，由于结构的大型复杂化，材料、工艺、安装误差及非线性，大量的简化及不确定因素等，要建立准确的数学模型本身就非常困难。

某大型液体火箭发动机再生冷却喷管十分复杂，其动特性对摇摆发动机伺服控制、动力学设计等均有重要影响，寻找喷管结构动力建模与模型修改的相应技术是当前研究的一项重要任务。杜飞平等[3]按刚度和质量等效原则将喷管简化为各向同性单层壳单元，邵松林[4]将喷管等效为正交各向异性3层壳单元。上述喷管建模只提及等效方法，并未对模型进行修正，所建模型精度偏低，且模型修正技术在液体火箭发动机中的应用也鲜见报道。

模型修正的基本思路与结构优化理论类似，其中基于灵敏度分析与优化算法的直接参数型模型修正应用最广泛[5-6]。文献[7-8]基于灵敏度分析以结构固有频率为目标函数对GARTEUR基准飞机模型成功进行了模型修正。由于参数型修正法所构建的目标函数通常具有高度非线性及多个局部极值点的特点，因此优化算法的选择对于问题的求解十分重要。模拟退火法(SAA)具有良好的全局寻优能力、稳健性等，目前已成为参数型修正方法的一个新热点。但是，采用传统SAA进行模型直接修正则收敛速度缓慢，算法性能与初值密切相关[9-10]；Rose[11]提出在确保一定优化质量的基础上，需对SAA进行改进以提高其搜索效率。

本文针对型号研制的实际需求，对整个模型修正过程进行研究，提出基于特征灵敏度分析与ISAA相结合的模型修正技术，在此基础上基于MSC Patran/Nastran开发了模型修正模块，并校验了该方法的有效性，研究表明该模型修正技术具有较高的工程应用价值。

1 参数化有限元建模及模态分析

某高压补燃液氧/煤油发动机喷管采用再生冷却形式的薄壁夹层板结构，由带螺旋铣槽内壁和外壁钎焊而成，内外壁材料不同，并在冷却环带附近设计了冷却套集液器，尺寸较大，刚度相对较小，其整体及局部截面如图1所示。

利用文献[12]提出的动力学建模方法，将喷管按双层壳模拟，并使用复合板属性。外壁具有较高的强度和刚度，提供弯曲刚度，为主要承载层，按各向同性材料考虑，取实际弹性模量和厚度。内壁(含中间层波纹状夹芯)主要提供剪切刚度，按正交各向异性材料处理，根据波纹夹芯结构复合材料等效理论，将其力学性能参数等效为垂直于板方向的剪切刚度GXZ、GYZ和拉压刚度EX、EY和泊松比μXY，取EZ=GXY=0。外壁较大的集液器采用与推力室主体模型一体的壳单元模拟，较小的集液器则采用偏置梁单元、与推力室主体模型相应部位共节点处理。建立的喷管参数化初始有限元模型见图2。

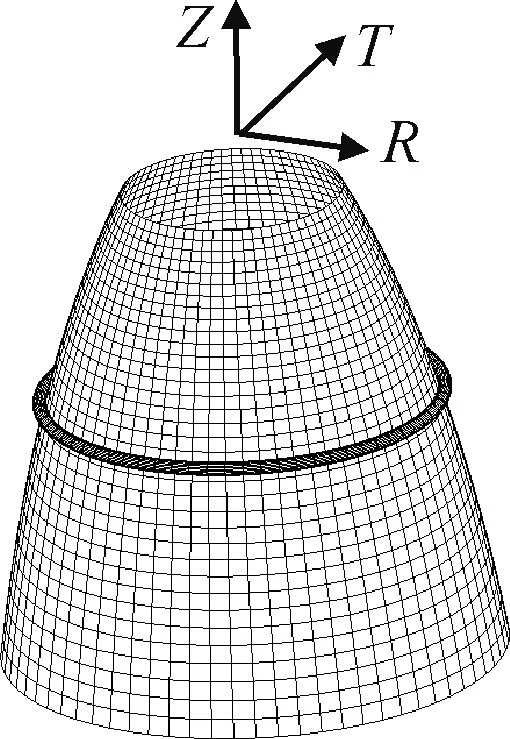
图2 喷管有限元模型Fig.2 FE model of nozzle

对喷管进行自由状态正则模态分析，提取前3阶模态，得到喷管结构的模态频率与振型。

2 模态测试

利用锤击法进行喷管模态测试。试验时，将喷管喷口朝下正放置于海绵垫上模拟自由边界，采用LMS Test.Lab模态分析系统、B&K4524B三向加速度传感器和B&K8206力锤，通过模态测试识别出喷管结构高精度的模态频率、振型及阻尼比等参数，其前三阶振型如图3所示。

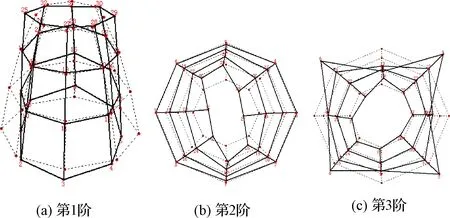
图3 喷管模态振型Fig.3 Modal shapes of nozzle

3 模型修正

模型修正的基本思想是通过不断改变有限元模型的参数，来促使模态分析结果和试验测试结果一致。本文建立了一种模型修正方法，通过灵敏度分析进行设计变量选取，并基于优化算法迭代寻优，其基本流程见图4。

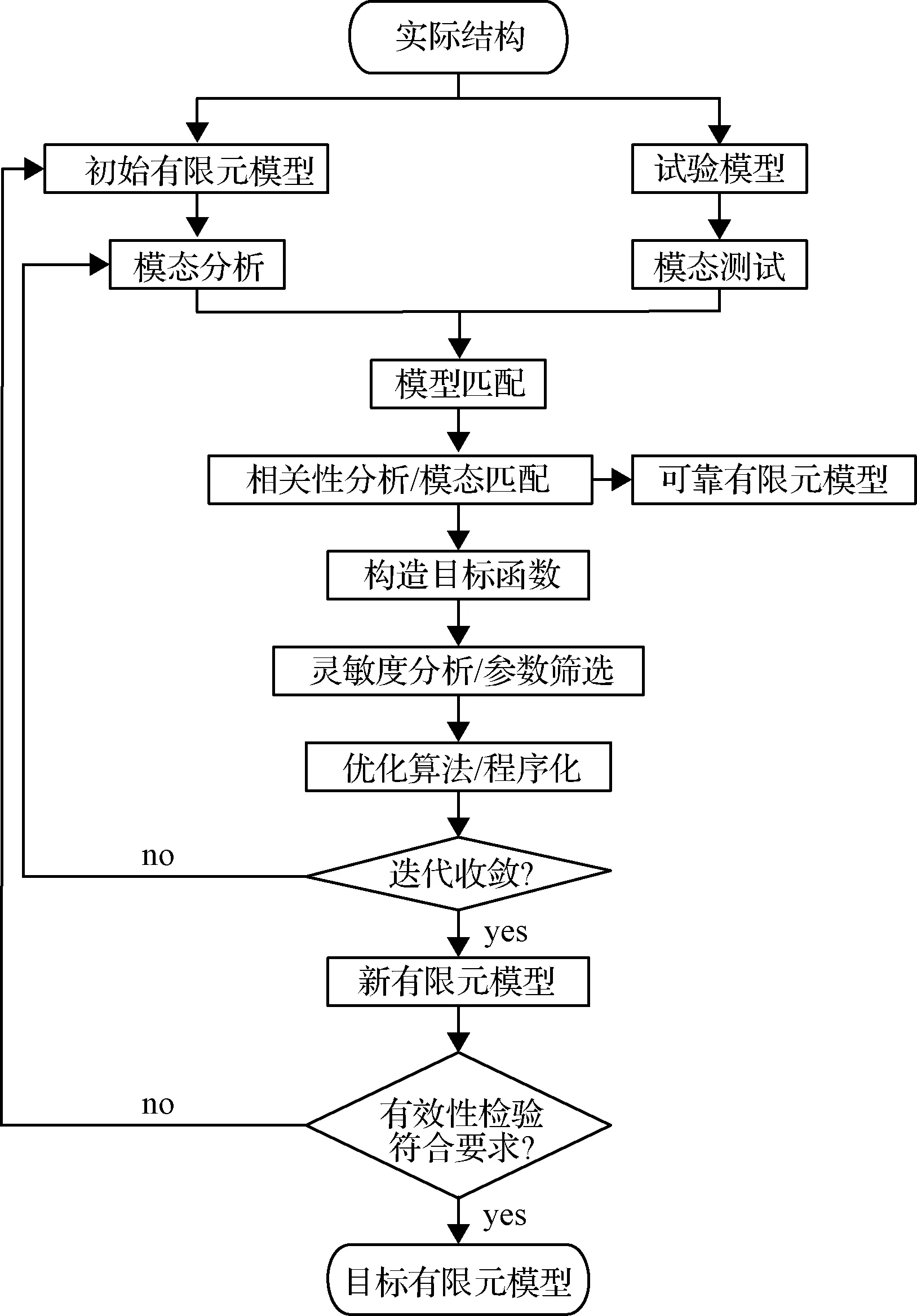
图4 修正流程Fig.4 Flowchart of model updating

3.1 模型匹配与动力相关性分析

为进行相关性分析，首先需要对理论模型、实验模型的自由度进行完全匹配。由于模态型缩聚法(MR法)能很好地保证缩聚前后所关心的低阶模态频率和振型非常好的吻合，故本文采用MR法对计算模型进行动力减缩，将计算模型的自由度减缩到试验测量自由度上形成一个“试验分析模型”(TAM)。相关性分析是判断有限元分析结果和试验结果在一定准则上相符程度的关键技术，本文采用以下判断标准

1)频率相关性

(1)

2)振型相关性，计算振型φa与实验振型φt的相关性通过模态置信准则(MAC，量符号记为C)来计算

(2)

试验与理论分析结果比较见表1。前三阶模态振型对应频率的相对误差最大达14.5%，MAC最小仅为0.61。文献[13]指出，修正后的有限元模型与试验模型之间的频率误差不超过±5%、MAC大于0.9 为相关性好的评价标准。因此，本文建立的模态分析模型不能准确反映实际结构的动力特性，必须对其进行修正，使其间的差异降低到可接受的水平。

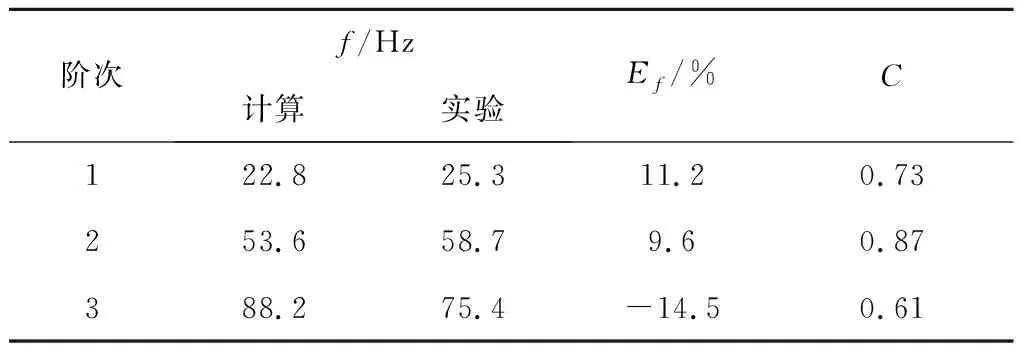
表1 计算与试验模态匹配表Table 1 The mode-matching of simulation and test

3.2 目标函数确定

由于模态频率反映结构的整体信息，振型包含结构振动行为的空间信息和局部信息，一个更加合理的方法是联合使用频率与振型作为目标函数，以提高模型修正的准确性。选取多目标优化构造的复合目标函数为

(3)

式中：p为设计变量，fa,j，ft,j分别为第j阶计算频率和与之对应的实验频率，Cj为理论分析与实验的第j阶模态振型的MAC值，n表示待修正的模态阶数；Wfreq,j，Wshape,j分别为第j阶模态频率权重和MAC值权重，当各阶模态频率及振型测试精度均较高时，不考虑权重的作用，取一致的加权系数或平均分配各加权系数。

3.3 修正参数选择

设计变量的选取原则多基于灵敏性分析，并兼顾初始模型的误差来源。在ISS-P5中针对灵敏度分析的不足，通过灵敏度分析和经验共同确定修正参数。经灵敏度分析，找出对结构总体动态特性影响最大、最有效的修正参数；利用模型误差诊断与误差定位技术，进一步确定待修改参数。因此，进行灵敏度分析与误差定位，使修改更具针对性和有效性，从而提高模型修正的质量与效率。

根据特征方程得特征值、特征向量灵敏度公式

(4)

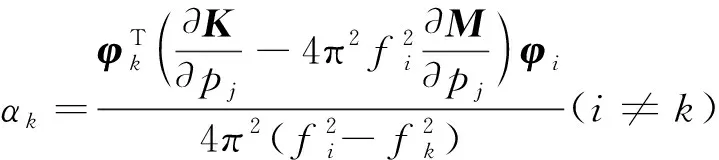
(5)

由于喷管外壁参数的确定性较高，故主要针对内壁选择参数，初选的修正参数有内壁厚度δ、密度ρ及μXY，GXZ，GYZ，EX，EY共7个参数。结合发动机喷管内壁结构尺寸、材料的实际情况与工程经验，同时为便于参数的敏度分析与模型修正迭代优化，本文给出参数一致的变化范围，将参数上下限定为原值的±20%。

基于MSC Nastran的设计灵敏度分析与优化功能(SOL200求解器)，在Matlab的GUI用户界面开发了设计灵敏度计算软件，循环调用计算/试验数据，进行相关性分析(MAC)→特征量、目标函数构造→参数选择→灵敏度分析(DSA)→确定最终设计变量。分析得目标函数关于设计参数的灵敏度见图5，μXY，GXZ，GYZ对目标函数的影响较小，因此在利用优化技术对模型进行修正时将这些参数从设计变量中剔除，最终确定的设计变量只有δ，ρ，EX及EY。

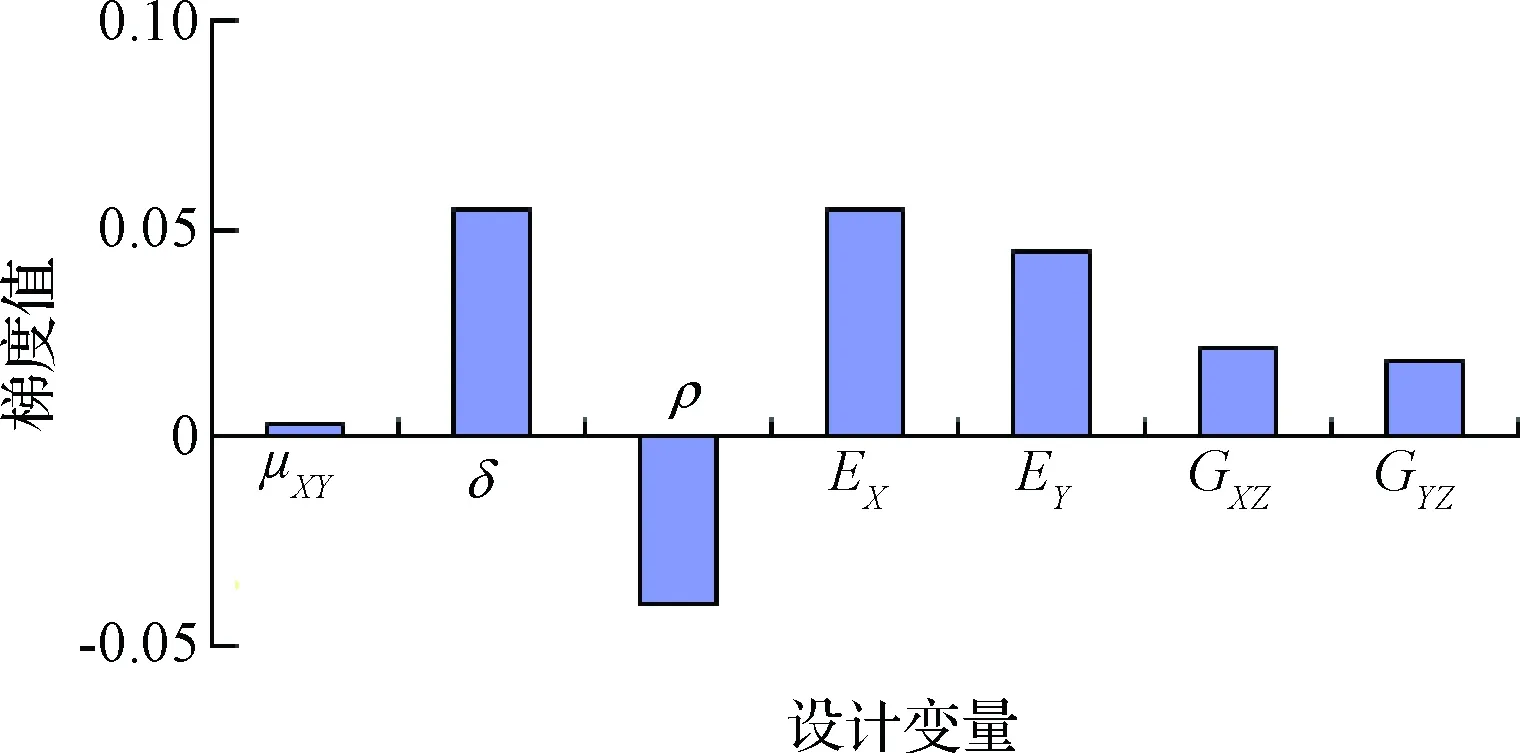
图5 目标函数对设计参数的灵敏度Fig.5 Sensitivity of objective function to design parameters

3.4 改进模拟退火算法

3.4.1 模拟退火算法(SAA)

SAA是一种基于Monte Carlo迭代求解策略的随机寻优算法，其出发点是一般组合优化问题求解过程与物理中固体物质的退火过程之间的相似性，目的在于为具有NP复杂性的问题提供有效的近似求解算法，是一种用于求解大规模组合全局优化问题的有效方法。退火过程由冷却进度表控制，包括控制参数T的初值T0及其衰减因子K，每个T值时的迭代次数L，Markov链长度及停止条件。优化问题的一个解xi及其目标函数J(xi)分别与固体的一个微观态ψi及其能量E(ψi)对应，进行“产生新解-计算目标函数残差-接受或舍弃”的迭代求解，算法主要流程为

(1)设定冷却进度表及初始解x0；

(6)

温度更新函数Tk=T0/(1+K)；

(3)Tk+1=Tk，若满足终止条件时退火结束，输出近似最优解xk，否则转入(2)。

3.4.2 改进模拟退火算法(ISAA)

经典SAA存在某些不足：退火速度问题，在温度较高时算法可以快速收敛到全局最优解，而到达最优解附近时速度明显变慢；由于采用Metropolis准则概率接受劣质解而遗失当前最优解，导致收敛

速度慢、波动性强；SAA在全局优化方面具有明显优势, 而在局部优化方面作用并不显著等。因此，为改善SAA的求解性能，本文提出改进模拟退火算法(ISAA)，改进思路如下：

一是对算法设置记忆器和增加返回随机搜索功能，以记住并返回曾经历的最优解；设变量X*和J*分别为记忆当前迭代的最优解及目标函数值。算法开始时令X*和J*分别等于初始解及其目标函数值；以后每接受一个新解时，就将当前解的目标函数值与J*作比较，若优于J*，就用当前解替代X*和J*；算法结束时，将所得最优解与记忆器中的解进行比较，取最优的一个作为此轮降温的最优解，避免了由于概率接受而遗失当前遇到的最优解，可以在一定程度上提高算法的稳定性。

二是在算法后链接一个局部搜索过程，以上步所得当前最优解为起点，用新解产生装置产生新解，再对所有所得最终解施行局部搜索，仅当优于当前解时接受，重复若干次后结束程序。局部搜索相当于“淬火”改善，通过“退火-淬火”结果比较，提高“退火”结果的可靠性，且可获得更好的近似解甚至整体最优解。

3.4.3 算法性能测试

为检验标准SAA与ISAA的性能，不失一般性，选取一个多极值函数进行测试[14]：

min (F)=x2+2y2-0.3cos(3πx)-

0.4cos(4πy)+0.7

(7)

约束条件：x,y∈[-100,100]，该函数最小值为F(0,0)=0；取冷却进度表为：T0=0.5，dT=0.5，Lk=20，Tk=1×10-4；初始解x=y=10。

采用SAA得到的解为：当x=y=-3.141×10-3时，F=5.308×10-4，这与最优解Fopt=0比较接近。而采用ISAA得到的解为：当x=y=-2.503×10-4时，F=2.963×10-6。经比较发现， ISAA的结果更接近最优解；进一步分析其优化历程发现，ISAA的收敛速度也更快。

3.5 动力学修正模块开发

基于MSC Patran/Nastran平台，利用DMAP语言对修正算法进行程序编制并嵌入到MSC Patran中，运用PCL语言在Patran中建立模型修正操作界面，整个过程是通过编写PCL程序以及调用外部算法自动进行的，从而二次开发出液体火箭发动机振动动力学分析模型修正软件ZDXZ V1.0(该软件已取得计算机软件著作权)，可对已建立的特定振动动力学模型在材料属性、几何参数等方面进行修正，程序整体框架如图6所示。

图6 程序流程图
Fig.6 Flow diagram of the program

软件具体架构如下：

(1)主界面，如图7所示。

图7 软件界面Fig.7 Interface of the software

(2)前处理主要用于快速生成模型相关参数，并为模型修正模块增加用户所需的附加设计参数。

(3)选择并声明优化变量，通过设置上下限将这些变量设定在具有实际物理意义的条件下。

(4)修正目标设定用于定义优化目标和约束。每一个模型修正参数的设定内容包括：参数名、类型(目标最大、目标最小)、对优化目标的权重、设计变量的上下限、初始值。在该模块中，需要添加实验数据或其他数据对目标优化算法进行比对，优化时每一步计算出来的结果都要与该数据进行比较，通过计算误差百分比，将各阶模态频率和振型的误差控制在要求范围内。

(5)修正过程控制模块提供常见的优化算法及工具。选择优化算法组成优化算法组合策略，并对算法运行进行控制。提供的优化算法包括：自编非线性序列二次规划，SAA、ISAA等。指定优化循环控制方式，在迭代修正过程中, 可以借助Patran软件进行参数化建模并反复调用Nastran软件进行求解。

(6)修正过程可视化及模型输出模块可读取优化结果文件，并对优化结果进行后处理，如输出优化参数数据、模型数据、选定优化步中的振型及固有频率等数据。

3.6 修正结果及有效性检验

采用多目标达到法进行迭代优化，收敛准则采取目标函数收敛容差小于1%，初始迭代步设为1000，优化程序在第403步收敛结束，最佳设计序列为第352步。模型优化前后的结果对比见表2，部分设计变量及状态变量迭代历程如图8所示。

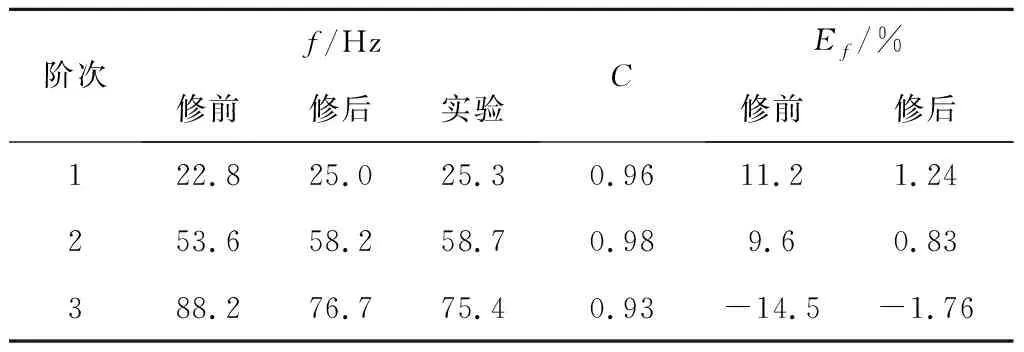
表2 喷管模型修正前后模态频率结果比较Table 2 The mode-matching of simulation by modified and original model to the test result

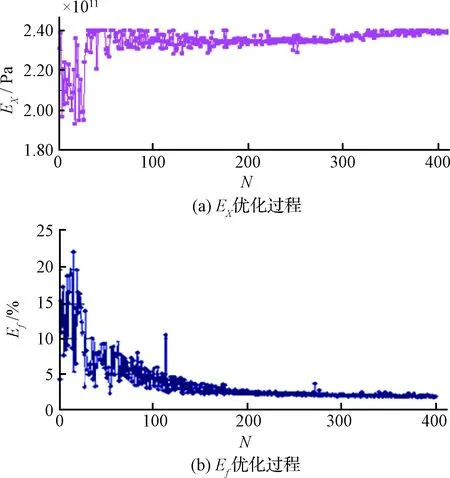
图8 迭代历程Fig.8 The iteration process

由表2可知，模型修正后，喷管结构的前3阶模态频率相对误差从14.5%下降至1.76%，MAC值从0.61提高到0.93。相比文献[5-6,13]的模型修正精度，本文所得结果的精度较高(高于频率相对误差小于±5%、MAC大于0.9的评价标准)。计算结果与实测结果一致性较好，最终所得的喷管结构动力学模型可以真实反映产品的实际动力学特性，修正后模型准确性可满足工程应用要求。

对本文的修正方法及分析结果的有效性进行检验。为防止该结果并非全局较优解，选择其他起始序列重新进行优化，同样得到本文的结果，说明该解确实是本优化问题的全局最优解，而非局部最优解。其次，选择试验测得的前3阶频率参与模型修正，试验测得的第4阶频率作为对修正后有限元模型的验证。第4阶试验、计算频率接近(在文献[11]要求范围内)，模型的动力计算结果与实测值基本吻合，从而证明了该方法的有效性。

文中的有限元模型规模为节点数2592，梁单元数71和四边形壳单元数2591，计算机配置为Intel Xeon E5-2643V3 3.4 2133 6C 1st CPU、Intel Xeon E5-2643V3 3.4 2133 6C 2nd CPU及主频2.60 GHz，采用在大范围粗略和局部精细的随机搜索+记忆功能的改进模拟退火优化算法(ISAA)进行多目标全局迭代优化，优化时间平均在110分钟。采用ISAA进行模型修正，具有优化质量高、稳定性好、收敛速度快及执行高效等优点。

4 结 论

以工程应用为切入点对模型修正技术展开研究，介绍了模型修正基础理论及其技术实现，研究结论如下：

1)将喷管简化为复合材料双层合壳结构，建立喷管参数化有限元模型；构建模态频率及振型的联合目标函数，基于动力信息特征灵敏度分析确定设计变量，建立了喷管结构模型修正优化模型；

2)以SAA为基础，利用设置记忆器和在算法后链接一个局部搜索过程的方法，提出一种改进模拟退火优化算法(ISAA)，经验证改进算法具有更高的收敛稳定性与收敛速度；

3)在MSC Patran/Nastran软件平台上二次开发了液体火箭发动机振动动力学分析模型修正软件，发展了基于模型修正算法的应用软件研制，该软件具有友好交互功能及强大数据管理功能，可实现对复杂模型的自动修正；

4)通过对喷管模型修正，前3阶计算、试验模态频率相对误差从14.5%降低至1.76%，MAC值从0.61升高到0.93，有限元模型精度和可靠性得以大幅度提高，修正后模型可为结构动力学设计、动态预测等工程服务；

5)对本文提出的模型修正方法进行了验证，该方法的有效性满足模型修正标准要求，且具有较高的修正质量与效率，适用于大型复杂结构的模型修正。

参 考 文 献

[1] 邱吉宝，向树红，张正平. 结构动力学及其在航天工程中的应用[M]. 合肥：中国科学技术大学出版社，2015.

[2] 贺尔铭，陈熠，李玉龙，等. 机翼双梁模型的动力学修正及应用[J]. 应用力学学报，2013，30(3):367-372. [He Er-ming, Chen Yi, Li Yu-long, et al. Dynamic modification and application of wing double-beam model[J]. Chinese Journal of Applied Mechanics. 2013, 30(3):367-372.]

[3] 杜飞平，谭永华，陈建华. 基于子结构试验建模综合的火箭发动机结构动力分析[J]. 推进技术，2015，36(10): 1547-1553. [Du Fei-ping, Tan Yong-hua, Chen Jian-hua. Structural dynamic analysis of rocket engine based on synthetic technology for substructure test model[J]. Journal of Propulsion Technology, 2015, 36(10): 1547-1553.]

[4] 邵松林. 某火箭发动机模态分析[J]. 火箭推进，2012，38(4):55-59. [Shao Song-lin. Modal analysis of a rocket engine[J]. Journal of Rocket Propulsion, 2012，38(4):55-59.]

[5] 丁继锋，韩增尧，马兴瑞. 大型复杂航天器结构有限元模型的验证策略研究[J]. 宇航学报，2010，31(2):547-555. [Ding Ji-feng, Han Zeng-yao, Ma Xing-rui. Finite element model verification strategy of large complex spacecraft[J]. Journal of Astronautics, 2010, 31(2):547-555.]

[6] 马睿，姜东，吴邵庆，等. 考虑重力影响的太阳翼模型修正方法研究[J]. 宇航学报，2014，35(12):1373-1378. [Ma Rui, Jiang Dong, Wu Shao-qing, et al. A modeling updating method for solar array considering the influence of gravity[J]. Journal of Astronautics, 2014, 35(12):1373-1378.]

[7] Mares C, Mottershead J E, Friswell M I. Result obtained by minimizing natural-frequency errors and using physical reasoning[J]. Mechanical Systems and Signal Processing, 2003, 17(1):39-46.

[8] Baklanov V S. Low-frequency vibroisolation mounting of power plants for new-generation airplanes with engines of extra-high bypass ratio[J]. Journal of Sound and Vibration, 2007, 308(3/5):709-720.

[9] 葛振振，周军，林鹏. 采用改进模拟退火算法的高速飞行器随控总体优化方法[J]. 宇航学报，2013，34(11):1427-1433. [Ge Zhen-zhen, Zhou Jun, Lin Peng. The control-configured optimization method for hypersonic vehicles using the improved simulated annealing algorithm[J]. Journal of Astronautics, 2013, 34(11):1427-1433.]

[10] 胡俊亮，颜全胜，郑恒斌，等. 基于Kriging模型的钢管混凝土连续拱桥有限元模型修正[J]. 振动与冲击，2014，33(14):33-39. [Hu Jun-liang, Yan Quan-sheng, Zheng Heng-bin, et al. CFST arch/continuous beam bridge FEM model updating based on Kriging model[J]. Journal of Vibration and Shock, 2014, 33(14):33-39.]

[11] Rose C. Low mean intermodal distance network topologies and simulated annealing[J]. IEEE Trans. On Communications, 1992, 40(8):1319-1326.

[12] 杜大华，贺尔铭，薛杰，等. 大推力液体火箭发动机启动冲击响应特性研究[J]. 西北工业大学学报, 2016, 34(6). [Du Da-hua, He Er-ming, Xue Jie, et al. Research on start-up impact response characteristics of large thrust liquid rocket engine[J]. Journal of Northwestern Polytechnical University, 2016, 34(6):982-989.]

[13] Chuang Y T. Mass matrix updating for model validation[C]. Proceeding of the 15thInternational Modal Analysis Conference. Bethel: Society for Experimental Mechanics, 1997:818-824.

[14] 夏露，常彦鑫，张龙. 改进模拟退火算法在翼型设计中的应用[J]. 飞行力学，2007，26(1):71-74. [Xia Lu, Chang Yan-xin, Zhang Long. The application of an improved simulated annealing algorithm to airfoil design[J]. Flight Dynamics, 2007, 26(1):71-74.]