高超声速飞行器新型预设性能控制器设计
冯振欣,郭建国,周 军
(西北工业大学精确制导与控制研究所,西安 710072)
0 引 言
高超声速飞行器乘波体气动布局构型和机身推进一体化设计能够带来高升阻比、低波阻等适用于高超声速巡航飞行的理想条件[1]。与此同时, 也引入了推进/控制/气动的严重耦合, 导致超燃冲压发动机推力对攻角变化非常敏感[2]。此外, 高超声速飞行器复杂的飞行环境及模型高度非线性问题也使得其飞行走廊变得非常狭窄。因此, 高超声速飞行器控制性能问题成为当下控制器设计的一个难点。
目前,高超声速飞行器控制研究取得了积极进展,典型如滑模控制方法[3-4],反步法[5],自适应鲁棒控制方法[6]等。上述方法虽然能够保证控制系统的稳态性能,即确保飞行器各状态跟踪误差最终收敛到零/零附近的小邻域内, 但是并未对飞行器的瞬态响应(如超调量, 收敛时间)做出限制。事实上,由于飞行姿态与发动机推力耦合严重, 不合适的跟踪指令/姿态变化过大都会使得发动机进气道流量捕获量下降, 导致发动机推力变化,进而降低飞行系统的控制品质。
目前解决这一类问题主要有两种思路:一种是直接对姿态角进行约束, 将姿态角的幅值约束在某个特定范围内, 从而降低发动机推力与姿态耦合因素对控制品质的影响。如文献[7]采用模型预测控制算法对高超声速飞行器的状态和控制输入进行了限制,但是该方法计算量较大;文献[8]在高超声速飞行器控制器设计中引入指令滤波器,该方法能够有效应对状态幅值、带宽、速率约束问题, 取得了较好的控制效果;文献[9]则采用积分型障碍Lyapunov函数方法解决高超声速飞行器攻角约束以及输入非线性问题, 满足了控制系统的需求。但是由于高超声速飞行器姿态与推进的耦合关系高度非线性, 因此无法精确给出攻角约束的边界。此外, 攻角测量困难也制约了上述方法的广泛应用。
另一种思路是对飞行器高度指令和速度指令进行限制, 间接降低控制系统对姿态角变化的需求。传统的方法是引入参考模型, 令飞行器高度和速度子系统分别跟踪参考模型给出的相应指令。但是考虑到飞行器气动参数大范围不确定和外部扰动的影响, 有必要对高超声速飞行器全过程跟踪轨迹进行限制。如文献[10]将预设性能方法引入高超声速飞行器控制器设计中, 该方法的基本思路是:设计预设性能函数, 即确保稳态跟踪误差收敛到一个预先设定区域的同时, 收敛速度及超调量满足预先设定的条件, 然后采用非线性映射函数进行误差转化, 最后针对新的非受限系统设计backstepping控制器, 从而兼顾了系统的稳态和动态性能。
本文提出一种基于时变障碍Lyapunov函数的新型高超声速飞行器控制算法, 结合动态面控制, 该方法可同时兼顾高度和速度子系统的稳态跟踪性能和瞬态响应, 且无需进行误差转化, 相比传统预设性能方法, 降低了控制器设计复杂度;同时, 设计自适应非线性干扰观测器对飞行过程中强不确定上界进行估计, 从而增强控制系统的适应性。此外, 本文还引入误差辅助变量以降低飞行器执行机构饱和特性对闭环控制系统的影响。Lyapunov理论证明了闭环系统的稳定性及有界性。
1 高超声速飞行器纵向运动模型
高超声速飞行器纵向平面动力学模型为[11]
(1)
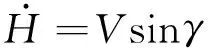
(2)
(3)
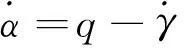
(4)
(5)
式中:V,H,γ,α,q分别为高超声速飞行器的速度、飞行高度、航迹角、攻角和俯仰角速率。Iyy,m,g分别为俯仰转动惯量、飞行器质量和重力加速度。T,D,L,Myy分别为发动机推力、空气阻力、升力、俯仰力矩, 可描述为
(6)
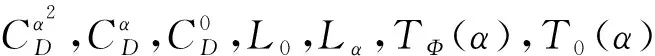
本文引入障碍Lyapunov函数理论解决飞行状态预设性能问题, 下面给出相关引理。

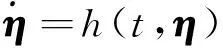
(7)
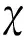
V→∞, 当|x|→kc
(8)
(9)
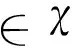
(10)
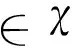
引理2[13]: 对于任意δ>0以及ε∈R,有不等式成立:
(11)
式中:tanh(·)是双曲正切函数。
2 控制器设计
控制目标:1) 飞行高度H和速度V分别稳定跟踪高度和速度指令(假设速度和高度指令及其导数均有界)且飞行过程中跟踪误差不超出预设边界;2)闭环系统所有状态均有界。
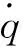
2.1 高度子系统设计
假设1. 由于高超声速飞行器巡航段攻角及航迹角变化较小, 可近似认为 sinα≈α, sinγ≈γ。
结合假设1, 令x1=H,x2=γ,x3=α,x4=q, 则高度子系统可描述为
(12)
式中:g1=V,f2=L0/(mV)-gcosx2/V,g2=(Lα+T)/(mV),f3=-(L+Tx3)/(mV)+gcosx2/V,g4=Mδe/Iyy,f4=(MT+M0(α))/Iyy,u=δe。di(i=1,2,3,4)包含系统非线性高阶截断误差, 参数摄动及外部不确定。
假设2. 式(12)中的干扰项di连续且满足|di|≤Di,i=1,2,3,4。Di为未知正常数。
结合动态面法, 高度子系统控制器推导过程如下:
1) 令z1=x1-x1d, 对z1求导可得
(13)
式中:z1为高度跟踪误差,x1d为高度指令。
设计新型时变障碍Lyapunov函数
(14)
式中:B1(t)=(kc1-kb1)e-c1t+kb1为高度预设边界函数, 其中,kc1为允许的最大初始高度跟踪误差,kb1为稳态误差边界,c1为收敛速度参数, 且均为正数。
注2.本文选取的边界函数B1(t)与传统的预设性能函数形式相同, 区别在于本文将该函数作为时变约束边界引入到障碍Lyapunov函数方法设计中, 而非误差转化和映射, 降低了控制器设计复杂度。
对式(14)求导可得
(15)
选取虚拟控制量x2c
(16)
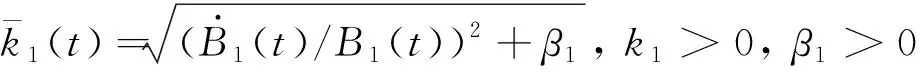
设计非线性自适应律
(17)
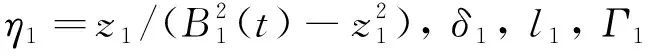
注3.为避免微分爆炸, 本文在每一步中引入一阶滤波器,以获取经过滤波器的虚拟控制量xid
(18)
式中:i=2,3,4,τi∈(0,1)为待设计常数。
定义误差z2=x2-x2d,y2=x2d-x2c, 式(15)写为
(19)
2) 对z2求导可得
(20)
选取虚拟控制量x3c
(21)
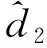
(22)
式中:η2=z2,l2,Γ2均为正数。
定义误差z3=x3-x3d,y3=x3d-x3c, 则有
(23)
3) 对z3求导可得
(24)
设计虚拟控制量x4c
(25)
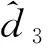
(26)
式中:η3=z3,l3,Γ3均为正数。
定义误差z4=x4-x4d,y4=x4d-x4c, 则有
(27)
(28)
式中:ξ为误差辅助变量。u为系统实际输入,uc为控制器产生的控制指令。ξ用来确保即使出现执行机构饱和, 控制系统依然稳定。
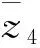
(29)
式(28)代入(29)可得
(30)
选取控制量为
(31)
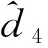
(32)
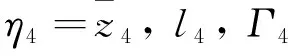
将式(31)代入(30)可得
(33)
定理1. 对于高度子系统(式(12)), 采用控制律(31), 若满足条件:①x1(0)
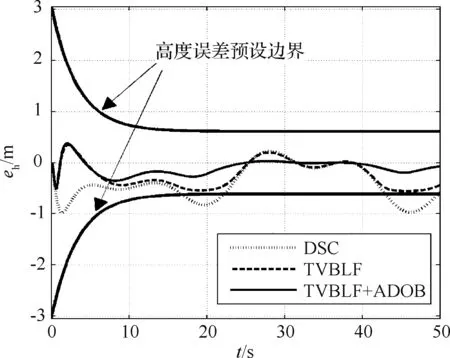
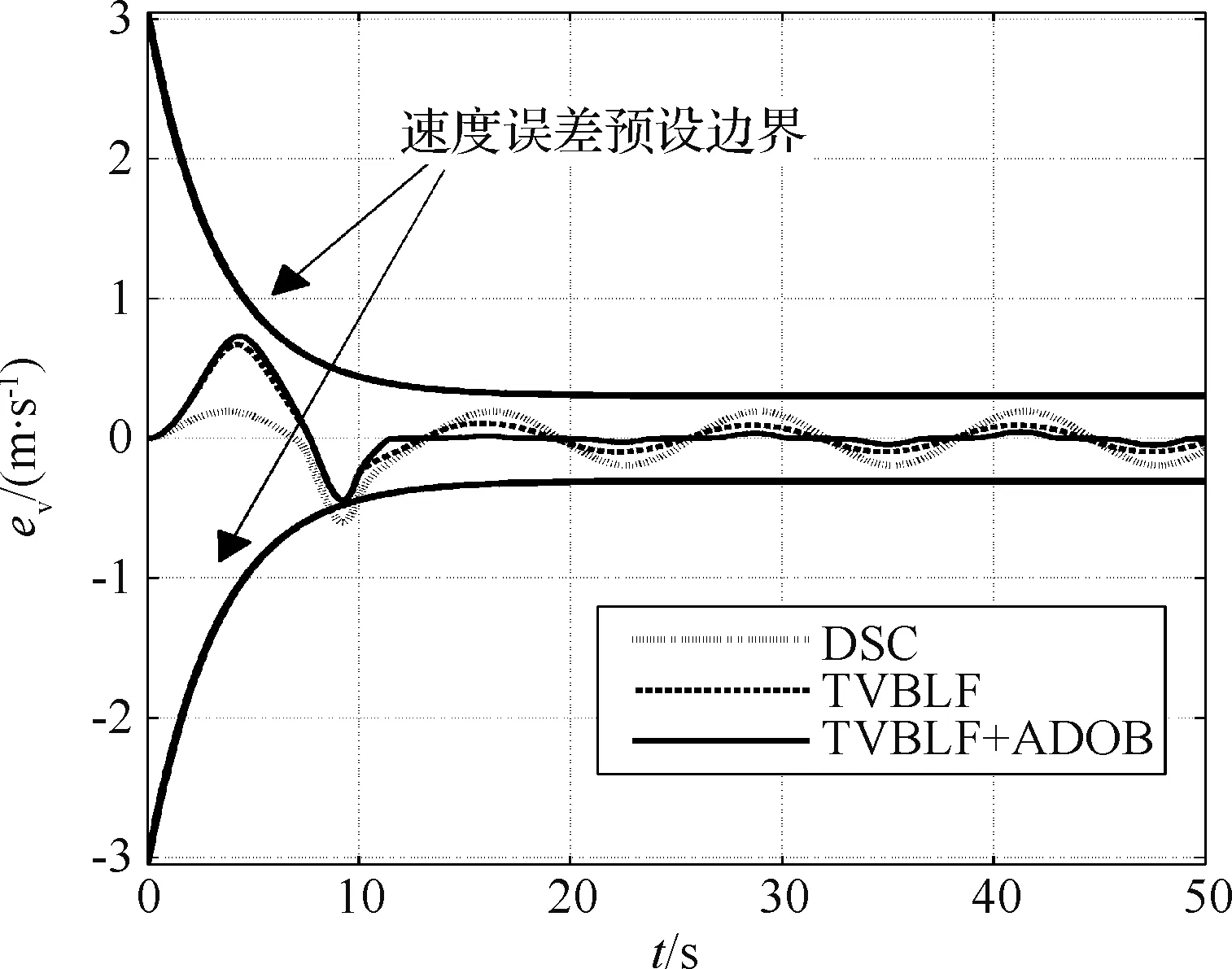
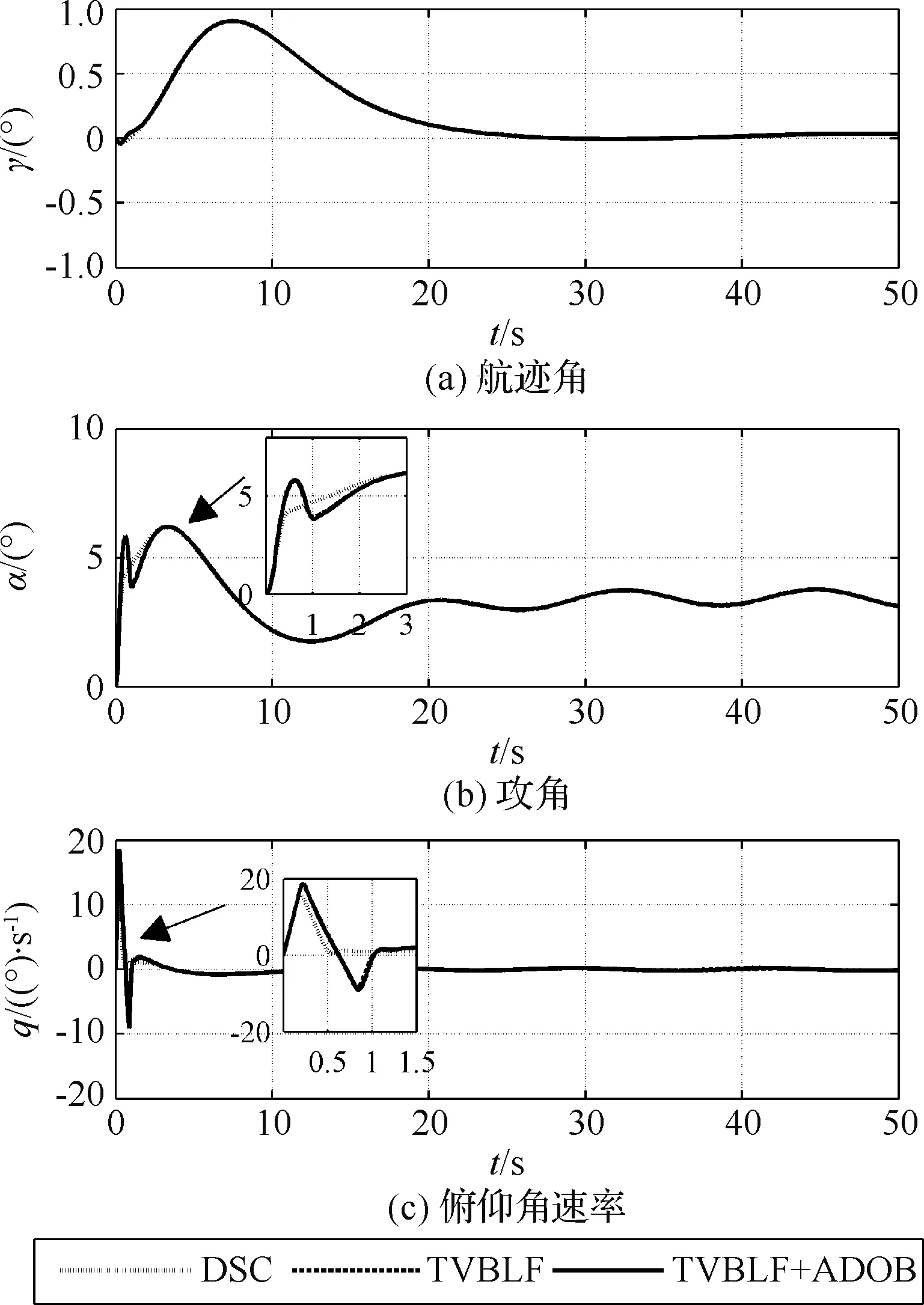
则高超声速飞行器高度跟踪误差全过程满足预设性能, 即|z1(t)| 证. 选取Lyapunov函数 (34) 式(34)对时间t求导, 将式(19), (23), (27), (33)代入得 (35) 由yi,i=2,3,4的定义可知,yi满足 (36) 定义Λi=max|xic(t)|,t≥0,i=2,3,4,τi>0, 由Young不等式 (37) (38) (39) (40) (41) 综合式(37)-(41)及引理2, 式(35)可进一步写为 (42) 若存在μ1>0满足条件②, 则式(42)可写为 (43) 1) 对式(43)两边同时积分可得 (44) (45) 设计新型时变障碍Lyapunov函数 (46) 式中:BV(t)=(kcv-kbv)e-cvt+kbv为速度预设边界函数, 其中kcv为允许的最大初始速度跟踪误差,kbv为稳态误差边界,cv为调节收敛速度参数, 且均为正数。 对式(46)求导可得 (47) 设计速度子系统控制器 (48) 采用自适应律估计不确定项d5的上界 (49) 式中:l5,Γ5均为正数。 将式(48)代入(47)可得 (50) 选取Lyapunov函数 (51) 对(51)求导并结合引理2可得 (52) 定理2. 对于高超声速飞行器控制系统(式(1)~(5)), 采用控制律(31)和(48), 如果满足条件:①x1(0) 证. 选取Lyapunov函数 W=W1+W2 (53) 式(53)对时间t求导可得 (54) 若存在μ>0且满足条件②, 则式(48)可写为 (55) 式中:β=β1+β2,μ=min{μ1,μ2}。 1) 对式(55)两边同时积分可得 W(t)≤W(0)e-μt+β/μ(1-e-μt) (56) 以某型高超声速飞行器纵向动力学模型对本文控制器进行校验, 模型及气动参数详见文献[11]。飞行器初始高度为25 908 m; 初始速度2310.384 m/s;γ0=0°,α0=0°,q(0)=0 rad/s,δe(0)=0°。实际控制量幅值限制为:Φ∈[0.05,1.5],δe∈[-20°,20°]。 速度子系统跟踪速度阶跃指令Vc= 121.92 m/s;高度子系统跟踪高度指令hc= 400 m, 要求飞行过程中高度和速度跟踪误差分别满足:|z1| (57) 选取控制增益kv=1.5,k1=2,k2=2,k3=20,k4=0.5,一阶滤波器参数τi=0.05(i=2,3,4),干扰观测器增益Γ1=1.5,Γ2=0.75,Γ3=0.015,Γ4=0.000 65,Γ5=0.2,l1=0.0001,l2=0.03,l3=l4=l5=0.1,δ2=0.001,δ1=δ3=δ4=0.1,δ5=0.01。 图1 高度及速度跟踪曲线Fig.1 Curves of height and velocity 图2 高度误差跟踪曲线Fig.2 Tracking error curves of height 图3 速度误差跟踪曲线Fig.3 Tracking error curves of speed 图4 航迹角、攻角和俯仰角速率变化曲线Fig.4 Curves of flight path angle, angle of attack and pitch rate 如图1~5所示, 在外部扰动作用下选取相同的控制参数对动态面法[3](DSC), 本文算法不加干扰补偿(TVBLF)和本文算法加干扰补偿(TVBLF+ADOB)三种控制方案进行校验。从两方面进行分析。 另一方面,对比无干扰补偿控制方案(TVBLF) 和有干扰补偿的控制方案(TVBLF+ADOB)。从图2、图3可以看出,两种方案作用下高度和速度跟踪误差均能满足预设性能要求, 但是显然引入干扰补偿的方案跟踪精度更高, 因此, 说明本文设计自适应干扰观测器能够提升控制系统的适应性和精度。此外, 本文引入辅助误差变量ξ抑制输入饱和带来的影响,因此当跟踪误差逼近边界时, 控制输入需求有所增加(见图5(b)), 与定理1结论一致。 针对高超声速飞行器强不确定及多约束问题,提出了一种基于动态面法的新型时变对数型障碍Lyapunov函数控制器。实现了高度和速度稳态误差收敛的同时, 还确保收敛速度、超调量等瞬态性能要求。设计了自适应干扰观测器对参数摄动及外部干扰的上界进行估计, 提高了控制系统精度和适应性。本文还引入误差辅助子系统补偿输入饱和的影响。仿真结果表明, 本文控制器兼顾了系统的动态和稳态性能, 且闭环系统所有状态均有界。 参 考 文 献 [1] 李惠峰, 薛松柏, 张冉. 吸气式高超声速飞行器机体推进控制一体化建模方法研究 [J]. 宇航学报, 2012, 33(9): 1185-1194. [Li Hui-feng, Xue Song-bai, Zhang Ran. Research of modeling method based on integrated design for airframe-propulsion-control of AHV [J]. Journal of Astronautics, 2012, 33(9): 1185-1194.] [2] Brocanelli M, Gunbatar Y, Serrani A, et al. Robust control for unstart recovery in hypersonic vehicles [C]. AIAA Guidance, Navigation, and Control Conference, Minneapolis, USA, Aug 13-16, 2012. [3] An H, Liu J, Wang C, et al. Disturbance observer based anti-windup control for air-breathing hypersonic vehicles [J]. IEEE Transactions on Industrial Electronics, 2016, 63(5): 3038-3049. [4] 刘宇超, 郭建国, 周军,等. 基于新型快速Terminal滑模的高超声速飞行器姿态控制[J]. 航空学报, 2015, 36(7): 2372-2380. [Liu Yu-chao, Guo Jian-guo, Zhou Jun, et al. Hypersonic vehicle attitude control based on new fast terminal sliding mode[J]. Acta Aeronautica et Astronautca Sinica, 2015, 36(7): 2372-2380]. [5] Wang F, Hua C, and Zong Q. Attitude control of reusable launch vehicle in reentry phase with input constraint via robust adaptive backstepping control [J]. International Journal of Adaptive Control and Signal Processing, 2015, 29(10):1308-1327. [6] Hu X, Wu L, Hu C, et al. Adaptive sliding mode tracking control for a flexible air-breathing hypersonic vehicle [J]. Journal of The Franklin Institute, 2012, 349(2): 559 - 577. [7] Tang W, Long W, Gao H. Model predictive control of hypersonic vehicles accommodating constraints [J]. IET Control Theory and Applications, 2017, 11(15): 2599-2606. [8] 董朝阳, 路遥, 王青. 高超声速飞行器指令滤波反演控制 [J]. 宇航学报, 2016, 37(8): 957-963. [ Dong Chao-yang, Lu Yao, Wang Qing. Command filtered backstepping control for hypersonic vehicle [J]. Journal of Astronautics, 2016, 37(8): 957-963.] [9] 冯振欣,郭建国,周军.高超声速飞行器多约束鲁棒姿态控制器设计 [J].宇航学报, 2017, 38(8): 839-846. [ Feng Zhen-xin, Guo Jian-guo, Zhou Jun. Robust attitude control design for a hypersonic vehicle with multi-constraints [J]. Journal of Astronautics, 2017, 38(8): 839-846] [10] Bu X, Wei D, Wu X, et al. Guaranteeing prescribed tracking quality for air-breathing hypersonic non-affine models with an unknown control direction via concise neural control [J]. Journal of the Franklin Institute, 2016, 353(13): 3207-3232. [11] Parker J T, Serrani A, Yurkovich S, et al. Control-oriented modeling of an air-breathing hypersonic vehicle [J]. Journal of Guidance, Control, and Dynamics, 2007, 30(3): 856-869. [12] Tee K P, Ren B, Ge S S. Control of nonlinear systems with time-varying output constraints [J]. Automatica, 2011, 47(4): 2511-2516. [13] Polycarpou M M. Stable adaptive neural control scheme for nonlinear systems [J]. IEEE Transactions on automatic and control, 1996, 41(3): 447-451. [14] Fiorentini L, Serrani A, Bolender M A, et al. Nonlinear robust adaptive control of flexible air-breathing hypersonic vehicles [J]. Journal of Guidance, Control, and Dynamics, 2009, 32(2): 401-416. [15] Xu B, Wang S X, Gao D X, et al. Command filter based robust nonlinear control of hypersonic aircraft with magnitude constraints on states and actuators [J]. Journal of Intelligent Robust System, 2014, 73: 233-247.
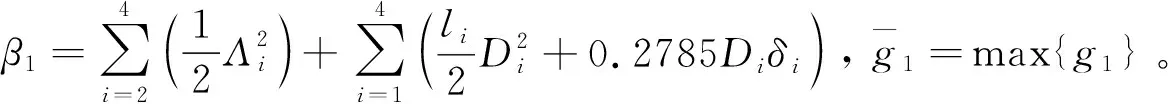

2.2 速度子系统设计
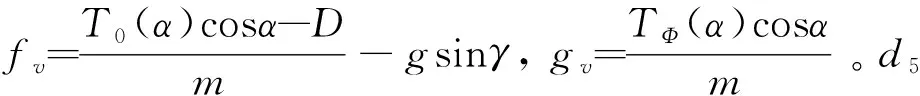

2.3 稳定性分析

3 仿真校验

4 结 论
——以大别山区9县(市)为例

