聚焦问题 追寻真实有效的课堂
陈秋蓉
(福建省莆田市城厢区沟头小学,福建莆田 351100)
引 言
面对课程和教材的变化,“问题解决”依然是大家百谈不厌的话题。自从把“两能”目标拓宽成“四能”目标,解决问题教学确实更为丰满、理性。但课改背景下解决问题的教学还面临一些困惑,如问题指向不明、问题肤浅没深度等。那么,如何聚焦“问题”,让解决问题教学更为厚实有效呢?本文着重通过几则案例加以阐述。
一、读懂情境,把握问题的起点
只有立足教材,读懂情境,提炼数学事实,才能使数学学习在真实的数学情境中“无痕”地进行,实现从实际问题到数学问题的无缝衔接。例如,人教版五年级下册第62页例3的“用公因数解决问题”,一位教师直接充分利用教材提供的情境素材,入课时让学生读懂题意,以简洁的语言描述:储藏室长16分米,宽12分米,要用边长是整分米的正方形地砖铺满,选择边长是几分米的地砖?边长最大几分米?随即教师抛出问题:本题铺地有什么要求?其实读题的同时学生已经可以从数学角度分析“整块”“正好铺满”的含义,即“整数块”“完整地铺”“正好铺满储藏室”“用正方形的地砖去铺”。一旦扫清这些字词理解障碍后,学生其实已经能够很好地把握问题的起点,很自然地触发问题,随后把目光锁定在“选择边长几分米的地砖”。教师巧借画图对问题加以分析,发现地砖的边长必须“既是16的因数,又是12的因数”,这样自动生成用公因数和最大公因数解决问题,得出“用边长1、2、4分米的地砖能铺满,最长应是4分米”,此时解决此类问题的策略浮出水面。
面对静止不动的教材,教师带领学生紧扣题中的关键句,经历审题的迷糊到明朗这一过程,将实际问题转化为数学问题,同时感受画图整理信息对于解决问题的重要性,顺利突破解题“盲点”。
二、顺势而为,掌握解决问题的策略
学生在解决问题的过程中有时不是一帆风顺的,在建模过程中也会走弯路,这时就要顺势引导,使学生敏锐地触及问题的本质属性,让教学更为灵动。例如,人教版四年级下册第10页例5的租船问题:一共32人,大船租金30元,限乘6人,小船租金24元,限乘4人,怎样租船最省钱?一位学生不假思索地回答:“两种船的租金不一样,租大船便宜。”另一位学生马上反驳:“空出两个座位,不是最省钱的”“坐满,没有空位,一定是最省钱”。教师顺势展示学生枚举1、2的两种方法。经过分析得出:尽量租大船便宜,而方案2虽坐满没有空位但不省钱,原因是小船租金多。第一次出现租金上的“谷底”,可课堂并没有浅尝辄止,出现另一种声音:“能否合租,会不会更省钱?”引发学生新的思辨并调整租船方案,发现方案4才是最省钱的,竟然再次出现“谷底”。租船方案如表1所示。
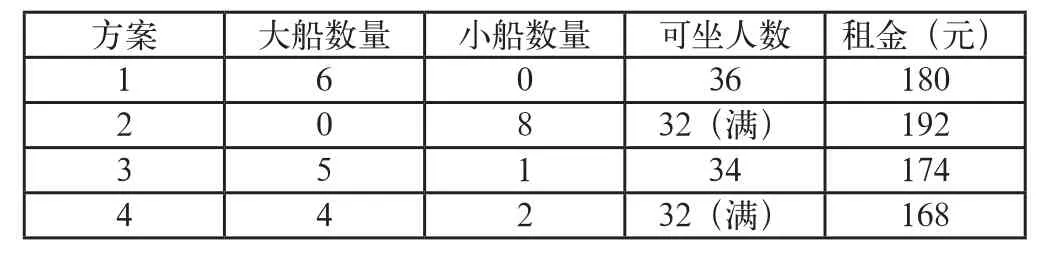
表1 租船方案
此时,有的学生坚持枚举继续探究,期待奇迹再次出现,但不再出现“谷底”,正是这一“失望”,学生才幡然醒悟,发现租船最省钱方案:“尽量租大船,不能有空位”。纵向比较悟出:坐满的方案有两个,但最优方案却只有一个。案例中的教师并没有急于表态,而是顺水推舟,把“球”踢给学生,用问题带动思维,真正做到胸中有丘壑,把每个细节做到极致。
三、变向调控,发现问题的本质属性
课堂教学宛若棋局,走进课堂,就是走进变化的棋盘。教师要冷静看待课堂的静与动,观棋落子,谋定而后动,这样才能突破思维的困惑点,发现问题的本质。例如,人教版六年级下册第27页例7,瓶子(图1)的内直径是8cm,这个瓶子的容积是多少?

图1
教师按照预案结合课件循序渐进地加以引导,原以为问题会迎刃而解,但讲授过程中发现课堂异常“安静”,很多学生还是处于迷茫和困惑状态。看着学生对问题一筹莫展,我突然醒悟:按部就班解决不了问题。于是我及时转向调整,先让学生回忆求不规则物体体积,感受转化思想,再让一名学生上台,结合实物演示瓶子倒置的过程,此时课堂热闹起来,学生思维活跃起来,问题接踵而来:“倒置前后,水的体积能不能直接求出来?”“空气的体积能不能直接求出来?”“能不能转化成圆柱呢?”其实此时已离解决问题的正确方向不远了,学生回头发现:“瓶子里水和空气的体积没变,两部分的体积之和就是瓶子的容积。经过这一系列分析,体验“等积变形”,问题的本质浮出水面。
很多时候教师与学生在理解问题的角度与深度上会有所偏差,教学会偏离预设轨迹,教师要凭借自己的智慧和应对能力,适时调控,让问题解决问题真正发生[1]。
四、适度留白,追寻问题的应对策略
教材呈现的内容是静态的,但其中也有许多“留白”。“留白” 给数学课本增加了“营养”。因此,课堂上适时“留白”,会取得“无声胜有声”的效果。例如,人教版五年级下册第99页例3“喝牛奶中的数学问题”, 这是新增的问题解决,最大的难点在于水和牛奶混合后第二次喝了一杯奶的几分之几,要解决1/2杯纯牛奶的一半一般是多少。这让暂无研究方向的学生暴露了思维的障碍点。教师在课堂上第一次“留白”:“你们读懂了什么?”“如何入手?”“用了什么办法让大家看得更明白?”这一系列问题作为思维“导火线”,引导学生投入积极思考中。经过思考,发现不管怎样兑水,牛奶剩下1/2 杯,再喝一半,就是喝了一杯牛奶的1/4 。感觉学生处于懵懂状态,教师再次“留白”,让学生选择自己喜欢的方式进行解释,此时学生结合直观图、画线段图、列表辨析,静静感受分离、竖分、列表等数学式的思考方法,用理性分离突破“加满水,水是1/2杯,纯牛奶还是1/2杯,又喝了1/2杯,这1/2杯里,一半是水,一半是纯牛奶”的思维障碍。也就是“第二次喝了1/4 杯牛奶, 1/4杯水”,这样抓住了变中的不变,发现数学中假设“分离”和现实“混合”的沟通。这样的留白,使学生对问题的理解从错误走向正确,从朦胧走向清晰,感悟数学的真谛[2]。
结 语
问题解决的数学课堂上教师要守住一颗平常心,冷静地审视,理性地思考,要及时锁定“问题”,激活学生的思维,引领学生深度学习。这样的课堂中,教师才会和学生一起慢慢成长。
[1] 朱伟森.让“问题解决”真正发生[J].小学数学教育.2017,(4):39-41.
[2] 陈国权.让学生充分经历解决问题的过程[J].小学数学教育.2015,(4):10-12.
——船舶承租人范围之观点厘清与浅要分析

