走向开放的数学学习
汪明峰
(江苏省苏州高新区实验小学校,江苏苏州 215000)
引 言
新课程理念下的小学数学教学,充分关注学生在课堂上的学习和发展,以学生已有知识经验为平台,从他们的最近发展区出发,构建更多适合他们的课堂探究活动形式,以促进他们主动参与,积极思考,热情合作,自主探究,从而形成稳固的认知结构,提高分析问题、解决问题等多种综合性数学思维能力[1]。
一、鼓励学生发出不同的声音,在真正思考中学有所得
课堂上,教师要舍得交出自己的话语权,让学生真正走到课堂中心位置,在“我实践”“我思考”“我提问”“我总结”……中活跃课堂气氛,调动学生主动性和积极性,灵动学生思维,走向真正意义上的主体主动学习。例如,在学习“表格列举”这一解决问题策略时,笔者设计了这样的题目:商店里有两种卡通贴画,其中小黄人贴画2张一组,海绵宝宝贴画5张一组,不拆开单卖。现在赵教师想买35张作为奖品分给孩子们,请你帮赵教师想想,他一共可以有几种买法?(温馨小贴士:从只拿一组5张的海绵宝宝贴画想起,按顺序列举)同学们经过思考、计算,都完成了表格,如表1所示:

表1 贴画购买方法
突然,有一个学生问道:“既然小黄人贴画可以买0组,海绵宝宝贴画也应该可以从买0组开始啊!题目为啥还提示我们‘从只拿一组5张的海绵宝宝贴画想起’呢?”“是啊,题目为什么这么提示呢?这不是漏掉了一种可能性吗?”“我们如果去掉这个提示,你会怎么做?”“我会从拿0组海绵宝宝贴画开始列举,虽然最后不成功,但我可以像后面那样画一根斜线,表示不成立。”“很好,你把每一种可能性都考虑到了!”“我会尝试从2张一组的小黄人贴画拿起,这样来列举。”……
虽然这位同学提出的方案不符合选择要求,但是从他的思考中,我们看到了一种可贵的思维品质:考虑问题需要尽可能全面,要想到多种可能性。教师的鼓励,让每个学生都由此得到了启发,并拿出了其他方案,虽然最后操作起来可能不及题目中提示的思路简洁,但毕竟真正思考过了。苏霍姆林斯基说:“每个人的心灵深处都有一种需要,那就是希望自己是一个发现者、研究者、探索者,而这种需要,在儿童时代最为强烈。”课堂上,教师把思考的空间交还给学生,把问的权力赋予学生,那么获得自主探究空间的学生交还给我们的,将是诸多大写的惊喜!
二、设计开放的问题情境,让枯燥的计算变得有滋有味
心理学家鲁宾斯坦说,问题情境往往是思维过程中最初的那一刻。带着问题去学习,学生才能有意识地调动已有的学习经验,积极探求解决问题的新方法,再苦再累也永葆热情。例如,学习计算长方形和正方形的面积时,我们如果抛出各种可能让学生去反复计算各种长方形和正方形的面积,他们将会怨声载道,产生极大的心理抗拒。因此,笔者设计这样的实践思考题,融枯燥的计算于有意趣的问题情境之中:一小区要在一座长80米的大楼前空地上建一个停车场,一共100米长的围栏,不要超出大楼两边,这样的停车场,可以有多少种建法?你觉得哪种建法最合理?
学生在这样的情境中兴趣盎然,在结合长度不超过80米、周长为100米这些条件后,列举了这样的可能:当长由40米逐渐减短,宽逐步加长时,它们相应的面积逐渐变大:40×10=400(平方米),39×11=429(平方米),38×12=456(平方米),37×13=481(平方米)……有同学列举得更直接:49×1=49(平方米),48×2=96(平方米),47×3=141(平方米)……还有的直接取整十数:40×10=400(平方米),30×20=600(平方米),20×30=600(平方米),10×40=400(平方米)……
教师将他们的列举结果投影呈示出来,他们很快发现,当长和宽的长度越来越接近的时候,停车场的面积也越来越大。笔者再让他们试试当长和宽都是25米的时候,结果怎样。他们惊讶地发现,这时候的面积达到了625平方米!也就是说,当长方形越来越接近正方形、甚至就是正方形的时候,面积最大。这时候,笔者不动声色地出示了三种建设规划图,如图1所示,第一个是图1的封闭图,也就是他们刚才一同指向的计算;第二个图是紧贴大楼建造的缺少一个边的建造方式,第三个图则是只有两边拦起的半开放式停车场。
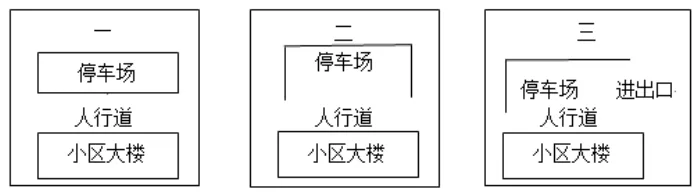
图1
他们立刻恍然大悟:原来,停车场不一定非要建成封闭的啊!于是再次兴致勃勃地规划、计算……数十次的计算练习,就在这样的寻找最佳建设方案中不知不觉地练习了,而且对长方形和正方形面积的关系,各种封闭、半封闭图形的周长计算也在思考中悄然完成。
三、合理变化灵活使用教材,让学生的学程进展更合理
开放的课堂需要教师活跃地思考、精心地设计。这样的开放,才开得有底气,开得有活力,开得有意义。面对不同的教学内容,我们尤其要合理、灵活地加以运用,使其真正具有开放意义,让学生的学程进展更合理,更顺畅,更具有可持续发展力量[2]。例如,教学“倒推”的解决问题策略,教材给出的例子是两杯果汁变化和晓军集邮数目变化的倒推问题。很显然,它们之间不存在情境统一的问题氛围,而且第一道题是两个人的果汁即两个量发生一次变化,第二道题是晓军的邮票数量这一个量发生了两次变化,由难到易,思维上也彼此孤立。
由此,笔者重新做了思考,设计了三个问题情境:(1)一杯果汁,小红喝去60毫升后,阿姨又给她倒了90毫升,现在杯子里一共是360毫升,请你算一算,这杯果汁原来有多少毫升?(2)小红和阿姨的杯子里一共有果汁420毫升,阿姨倒给小红90毫升后,两个人的果汁一样多。她们两人原来各有多少毫升的果汁?(3)小红、阿姨、妈妈三个人的杯子里共有果汁1250毫升,妈妈倒给阿姨50毫升,阿姨又倒给小红30毫升,现在,三个人的果汁一样多。她们三人原来各有果汁多少毫升?
这样,学生在同一个情境中由浅入深,循序渐进,他们在第一道题一杯果汁的变化基础上,掌握了倒推基本思路,而后在后面两个量发生一次变化,三个量分别发生两次和一次变化,从整理、画图、倒推、检验等数学活动、在变与不变中掌握倒推的思维策略,体验解决问题后的快乐。
结 语
尊重学生原有的知识经验,并让其成为解决新问题的生长点。精心设计走向开放的课堂环节,让数学课堂充满情趣,让学生的思维在开放中变得活跃,继而让学生的数学学习能力得到有效提升,数学素养得到真正培育。
[1] 景俊伟.小学数学开放式教学的实践探索[J].甘肃教育,2015,(19):91.
[2] 刘金山.小学数学开放式教学模式研究[J].生活教育,2015,(23):76-77.

