一种基于流形学习的PCA-SLPP特征空间降维方法

王培珍，王 慧，刘 曼，王 高，张代林

（安徽工业大学a.电气与信息工程学院；b.煤的洁净转化与综合利用安徽省重点实验室；c.冶金减排与资源综合利用教育部重点实验室，安徽马鞍山243002）

关健词：降维；主成分分析；流形学习；有监督的局部保留投影；煤岩；分类

对于复杂问题的分类与识别，常常会因为特征量过多致使特征空间维数过高而遇到“维数灾难”问题。因此，采用适当的方法对特征空间进行降维，即在保留数据信息的同时将高维特征空间嵌入到一个相对低维的空间中，成为提高分类器泛化能力和分类、识别正确率的重要手段之一。主成分分析法(principal component analysis，PCA)[1]和线性判别分析法(linear discriminant analysis，LDA)[2]是两种常用的降维算法，两者均通过一定的准则寻找变换矩阵，对特征量进行投影，并通过适当的截取实现降维。PCA的准则是使降维后数据具有最大方差，得到的是最佳描述特征，但非最佳分类特征。LDA方法其投影方向数受到限制，对数据样本类别数不多、且难以用少量特征量描述的复杂对象分类不适用。

人类主要通过低维流形信息认知事物[3]。Nayar等[4]指出高维的图像数据中具有低维流形现象，PCA和LDA提取的均为全局特征，难以反映高维数据的非线性流形结构。流形学习算法主要有等距映射算法(isometric mapping，ISOMAP）[5-6]、局部线性嵌入(locally linear embedding，LLE)[7]、拉普拉斯特征映射(Laplacian eigenmap，LE)[8]以及局部保留投影(locality preserving projection，LPP)[9]等。其中，LPP是一种非监督的局部特征提取算法，该算法通过最小化低维投影后样本与其近邻点之间距离的加权平方和，使原始空间中相邻的样本在降维后的低维空间中也保持相邻，以保留原始数据的局部结构。该算法没有考虑样本类别信息，对于分属于不同类别但在原特征空间靠得较近的数据点，投影后依然靠得较近甚至发生混淆，不利于特征区域的划分。为此申中华等[10]提出有监督的局部保留投影算法(supervised locality preserving projects，SLPP)，对于同类别相邻点与不同类别相邻点设置不同的惩罚项，以兼顾局部保留性和类间离散性。此类方法均没有考虑样本的全局结构。

煤岩在漫长的形成过程中受各种不确定因素的影响，结构较为复杂，采用少量特征量难以对其进行完备描述[11]；其特征量之间存在一定的相关性，若将诸多特征量简单联合则特征空间维数过高，且数据间存在大量的冗余，给准确分类带来困难[12]。鉴于PCA对数据的最佳描述能力和SLPP的局部保留特征，本文在PCA与SLPP的基础上，同时考虑样本数据的全局结构和局部保留特性以及样本类别信息，提出一种基于PCA-SLPP流形学习的特征空间降维方法，并将该方法应用于煤岩惰质组显微组分的分类，以验证本文方法对于具有复杂结构图像分类的有效性。

1 降维方法

1.1 主成分分析

主成分分析(PCA)法依照投影后特征值间方差最大的原则利用矩阵变换将一组相关变量映射为相互独立的变量，并依照方差大小排序。设有样本集X=[x1,x2,…,xn]，xi∈Rd,i=1,2,…,n；d为原始特征空间的维数。

先求样本集均值

再将每个样本中心化,

得到新样本集Z=[z1,z2,…,zn]，zi∈Rd。求样本集Z的协方差矩阵ZZT的特征值λi和对应的特征向量ai，且有

从大到小依此取前r个特征值对应的特征向量构成投影矩阵UPCA=[a1,a2,…,am]xi∈Rd×r，投影后的样本集。可根据积累贡献率[12]从大到小截取适合数量的特征量（保持原始数据的绝大部分的信息），则原始样本集X被映射到一个低维空间中，实现降维。

1.2 有监督的局部保留投影及其改进

局部保留投影(LPP)算法在保留类内局部结构的同时最大化类别之间的分离度。设有样本集X=[x1,x2,…,xm]，xi∈Rr，i=1,2,…,n；r为特征空间的维数。寻找投影矩阵 A=[a1,a2,…,am]∈ Rr×m，将样本映射到一个低维空间中，投影后的样本集为Y=[y1,y2,…,yn]，且Y=ATX，则LPP的目标函数[10]为

其中S为相似度矩阵。LPP中，对于邻近的样本点xi和xj，无论其是否属于同一类别，均按相同的规则进行投影，亦即其在投影后的特征空间中依然邻近，因而投影后空间样本的可区分性未能得到加强。为此，在SLPP中，将类内与类间样本区别对待，分别定义样本类内相似度矩阵W和样本类间相似度矩阵B[10]，对于类内结构的保留，采用最小化来实现；对于类间结构，则通过最大化实现。于是，SLPP的优化问题可表示为

其中，LB=diagB-B，LW=diagW-W，是拉普拉斯矩阵，diagB与diagW的元素分别为样本的类内和类间相似度矩阵B和W的对应行或列上的元素之和(B和W均为实对称矩阵)。最大化目标函数式(6)可转化为求下面广义特征值问题

取解出的前d个最大特征值对应的特征向量构成投影矩阵USLPP。

文献[10]中，需先构建连接图，在此基础上计算相似度矩阵。本文通过核函数，重新定义W和B为

其中：exp(-||xi-xj||2/t)为热核(heat kernel)函数，参数t为大于零的实数；||x||2为向量的L2范数。

改进后的SLPP，省去了连接图的构建，使算法可自适应地确定邻域范围，且更为高效简洁。

1.3 基于PCA-SLPP的降维方法

综合考虑PCA对数据的全局描述能力、SLPP对数据类内局部流形的保留特性及类间数据的可分离性，采用PCA计算降维映射矩阵UPCA，在此基础上，计算SLPP的投影矩阵USLPP，并生成最终的映射矩阵UPCA-SLPP，通过空间映射，实现最终的降维。具体步骤如下。

1)对样本进行PCA映射，按照式(3)求投影矩阵UPCA，将d维原始样本数据X通过投影矩阵投影到一个低维的r(1≤r≤d)维空间中。

2)使用热核函数建立类内相似度矩阵W和类间相似度矩阵B，计算对应的拉普拉斯矩阵LB，LW，求解式(7)的广义特征值问题；取特征向量a的前m个最大特征值对应的特征向量构成投影矩阵USLPP，将r维的数据进一步降维到一个更低维的m(1≤m≤r)维空间中。

3)计算最终投影矩阵UPCA-SLPP=UPCAUSLPP，依此计算投影结果Y=UPCA-SLPPTX，实现最终的特征空间及数据降维。

2 分类方案

2.1 煤岩惰质组显微图像特点

根据煤岩显微组分的形态特征和细胞结构等特点，惰质组分为丝质体、半丝质体、真菌体、氧化树脂体、粗粒体、微粒体、碎屑体等7个显微组分，其中丝质体又分筛状丝质体和星状丝质体2个亚组分[13]。其在油镜反光下典型显微图像如图1[14]。

图1 惰质组显微组分典型图像Fig.1 Typical microscopic images of inertinite

由图1可看出，不同显微组分在亮度（灰度）、形状、区域大小等方面各有特点，且表现出明显的纹理特征。但由于其结构复杂，不同组分间特征又有交错，少量特征难以描述。

2.2 特征量选择与提取

鉴于以上分析，同时为便于与文献[12]比较，分别从亮度和纹理的角度构建初始特征量集，对煤岩惰质组显微组分进行描述。

2.2.1 灰度统计特征量

依据镜质组不同组分在油镜反光下呈现的的亮度差异，从灰度统计的角度构建6个特征量。

1)亮度比

其中：c为亮度比，反映亮灰度值像素点在整个区域所占的比重；h(i)为灰度值为i的像素数；L为灰度级；e为设定的阈值。

2)均值

其中：μ为均值，反映图像的亮暗程度；p(i)为灰度值为i的概率。

3)方差

其中σ为方差，反映灰度对比度的大小。

4)三阶矩偏度

其中α为三阶矩偏度，反映灰度分布的不对称程度或者偏斜程度，当α＞0时为正偏斜；当α＜0时为负偏斜。

5)一致性

其中U(i)为一致性，反映纹理的粗糙度，一致性值越小，表明纹理越粗糙。

6)峰度

其中β为峰度，反映灰度分布的集中程度。

2.2.2 基于灰度共生矩阵纹理特征

灰度共生矩阵中的每个元素P(i,j|l,θ)描述的是原始图像中方向θ上间隔为l的一对像素值分别i和 j的像元出现的频数，θ通常取0°，45°，90°和135°。在此基础上定义5个反映纹理特征的参数。

1)能量

反映图像灰度分布的均匀性和纹理的粗细程度，其中L为灰度级。

2)熵

用于描述纹理的非均匀程度，越复杂纹理对应的熵值越大。

3)惯性矩

纹理越细，惯性矩越大。

4)局部平稳性

度量纹理局部变化平稳性，其值越大，局部越均匀。

5)最大概率

反映纹理出现次数最多的单元比例，其值越大，纹理一致性越强。

初始特征量集由上述11个特征量构成。如果直接采用上述11个特征量对初始特征量集进行分类，则对于显微组分中的每个样本，将在由上述11个特征量构建的11维特征空间中进行描述。其特征空间维数过高，且特征量间存在一定的相关性，特征数据存在大量冗余。为此，本文采用1.3描述的基于PCA-SLPP方法对特征空间进行降维，其中PCA主要用于去除特征量间的相关性，改进的SLPP用于在保持特征空间数据局部流形的前提下，对特征空间进一步降维，在降低分类器复杂性的同时，提高分类的正确率。

2.3 分类器构建

焦岩惰质组的分类属于小样本非线性分类问题，分类器采用支持向量机，其最终的决策函数可以表示为

其中：ai为拉格朗日乘子；b为阈值；xi是输入模式；δi为对应于xi的输出；K(xi,x)为核函数，用于解决分类的非线性问题。

研究表明[12]，当缺少过程的先验知识时，径向基核函数(RBF)在参数优化的条件下具有更好的性能。故本文选择RBF的核函数，形式为

其中σ2为函数的宽度参数，控制函数的径向作用范围，其值通过cross validation优化选取。

3 实验与结果分析

为验证方法的有效性，以煤岩惰质组显微组分为对象，分别采用单一的PCA，SLPP及本文方法对其特征空间进行降维，探讨不同降维方法及参数选取对分类效果的影响。实验平台硬件配置为Windows 764 bit，CPU i7-4700MQ，2.5 GHz，内存6 GB，算法在Microsoft Visual Studio 2013环境下编程实现。

3.1 实验数据及参数设置

实验所用的样本数据为煤岩惰质组显微组分图像，采用光度计在油浸反光下，依照GN/T 8899—1998标准采集。训练数据样本和测试数据样本均含8类，分别为筛状丝质体、星状丝质体、半丝质体、真菌体、氧化树脂体、粗粒体、微粒体、碎屑体，每类15个，共120个样本图像，大小为120×240。为避免数据量纲不同而导致降维和分类器训练过程中产生的中心偏移，对实验数据进行归一化处理[14]。

3.2 结果与讨论

3.2.1 热核参数t对分类结果的影响

为考察热核函数 exp(-‖xi-xj‖2/t)中参数t对分类结果的影响，取t=1～6采用本文方法分别进行实验，结果见图2，横坐标为最终维数。从图2可以看出，参数t对本文方法的分类结果稍有影响，且在降到较低维数时，影响较为明显，t=2时分类正确率较为稳定，且略高于其他取值。本文后续的比较实验中，热核函数参数t取2。

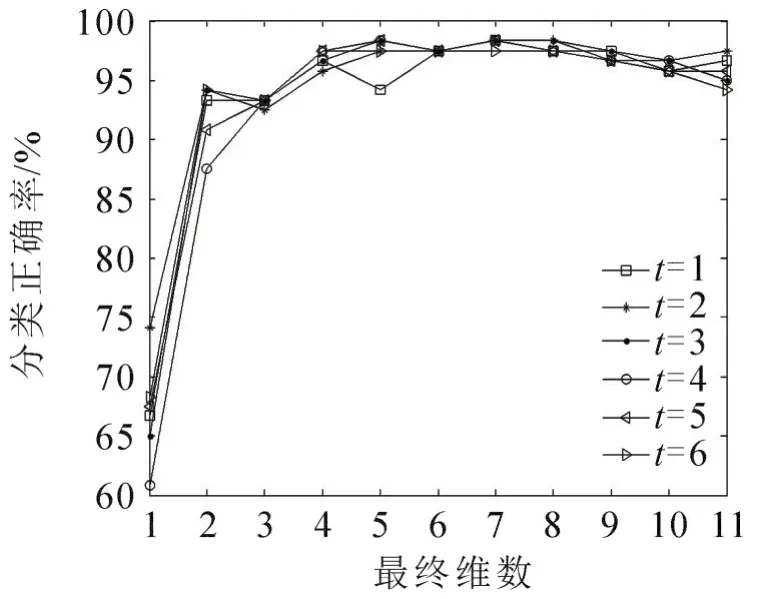
图2 参数t不同取值时分类正确率Fig.2 Classification accuracy with different parameters t

3.2.2 不同降维环节维数截取对算法性能的影响

为考察不同降维环节截取的降维维数对算法性能的影响，分别选取不同PCA降维维数r、SLPP降维维数m进行实验。表1是本文PCA-SLPP降维方法在参数r和m取不同值时的分类正确率，其中r和m的范围均为1～11，且m≤r。图3是当r分别取7、8、9、10，m取不同值时的分类结果。由图3可看出，当r一定时，分类正确率随着m的增大呈上升趋势，直至平稳，且m从1增大到2时分类正确率提升较大，表明局部结构的保留对分类效果有较大影响。图4是m分别取2、3、4、5时，分类正确率随r的变化情况。由图4可看出：m＝2时（m过低），分类正确率不稳定；m＝3～5时，分类正确率随着r的减小出现先略微增大后减小的趋势，如当m＝5，r从11减小到9时，分类正确率从90.83%上升到97.50%；继续减小r至5，则分类正确率下降到94.17%，表明PCA在逐渐减少主成分个数的过程中，数据间相关冗余逐渐减少，对于分类不利的影响逐渐消除；但减少到一定程度后再次减小，则会使用于分类的有效信息逐步丢失。

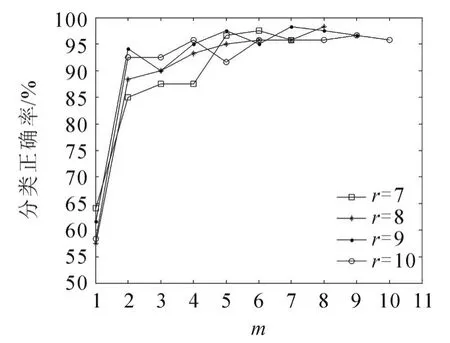
图3 维数r一定时分类正确率随m的变化Fig.3 Change of classification accuracy with m while r is fixed

表1 维数r、m不同取值时PCA-SLPP的分类正确率，%Tab.1 Classification accuracy of PCA-SLPPwith different values of r and m,%

3.2.3 不同降维方法分类结果比较

PCA-SLPP与PCA、SLPP在不同降维维数下的分类正确率结果见表2。对比结果可以看出：在较高维（维数≥7）空间中3种方法的分类正确率比较接近，维数为11时（与初始特征空间维数一致），PCA投影后分类结果最好，因为此时尽管特征空间维数保持一致，但将特征量投影到彼此正交的空间，减少了对分类产生不利影响的相关性因素；在特征空间维数降到较低（原样本空间维数的1/2及以下）时，本文方法（PCA-SLPP）分类正确率较PCA和SLPP均明显提高，高出近10%。

表3为数据样本降维至2维时各方法在不同处理过程中的耗时，包括求解投影矩阵时间、投影时间和分类时间。由表3可以看出，对于求解投影矩阵的时间，PCA耗时最短，约为其他方法耗时的1/10，因为其算法只需对样本数据的协方差矩阵进行特征值分解，而其他方法求解过程相对较复杂。3种方法对于投影时间基本相同，投影过程均为样本数据矩阵和一个具有相同大小的矩阵作乘法运算；分类时间也基本相同，其差别主要与分类器的结构有关。

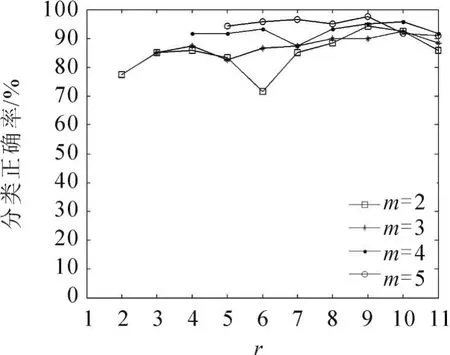
图4 维数m一定时分类正确率随r的变化Fig.4 Change of classification accuracy with r while m is fixed

表2 不同方法的分类正确率，%Tab.2 Classification accuracy with different methods,%

表3 各方法在不同处理阶段的耗时，μsTab.3 Time consuming of each method in different processes,μs

4 结 论

结合主成分分析和局部保留投影算法的优点，同时考虑样本数据的全局结构和局部保留特性及样本类别信息，提出基于PCA-SLPP的流形学习的降维方法，且将其应用于煤岩惰质组显微组分分类，得以下结论：

1)PCA可有效去除特征数据间的信息冗余，有助于提高分类正确率；

2)当PCA的维数一定时，随着SLPP维数的降低，分类正确率相对平稳，但当总维数降到2及以下时，分类正确率迅速下降；

3)对于具有复杂结构图像的分类问题，在样本空间维数降到原样本空间维数的1/2及以下时，本文提出方法的分类正确率明显高于其他同类算法；

4)本文算法在耗时上与SLPP相近。