基于响应耦合子结构法的机床动力学特性分析

欧淑彬，于秀娟，范登科

(1.安徽工业大学机械工程学院，安徽马鞍山243032；2.合肥国轩高科动力能源有限公司安徽合肥210011)

现代工业对数控机床等高档加工装备的性能要求越来越高，特别是在航空工业中，涡轮机叶片、飞机机翼等大型复杂工件的加工制造对机床的切削速度、加工精度及稳定性提出了更高的要求[1]。为保证机床加工精度，提高加工效率，研究刀具中心点(tool center point，TCP)整个工作空间动力学特性至关重要。王磊等[2]采用集中参数法建立轴间耦合三轴联动机床系统的动力学模型，研究机床在工作空间内的动力特性变化；刘海涛等[3]应用有限单元法获得机床频响函数在工作空间的变化。他们的研究局限于少数低阶固有频率和模态，影响动力学模型的分析精度。Law等[4]运用子结构综合法研究工作空间内机床动态特性，保留了对TCP影响较大的中高阶模态，但整机高阶动力学特征方程的求解无形中提高了计算成本。

美国学者Jetmundsen等[5]首先提出响应耦合子结构法(receptances coupling substructure analysis，RCSA)并用于直升机机体振动分析。王二化等[6]，朱坚民等[7]基于RCSA推导机床刀尖点的频响函数，采用实验和仿真相结合的方法辨识刀具-刀柄的刚度和阻尼系数；Montevecchi等[8]，Mancisidor等[9]采用一种改进的RCSA法预估不同加工刀具TCP的频响特性和稳定切削条件。RCSA法是将子结构的频率响应函数在不同位置处综合，获得组合部件频响函数的方法，避免了整体高阶动力学特征方程的求解，具有较高的计算效率。鉴于此，笔者将该方法运用于机床动力学分析，将机床分为主轴和床身两个独立的子结构，分别建立有限元动力学模型，在Z方向维度的不同位置进行频域综合，获得机床TCP的频率响应函数(frequency response functions，FRFs)，以期为切削稳定域研究提供理论基础。

1 机床RCSA动力学建模

机床是由床身和主轴组件构成的多体系统(如图1)，建立整体坐标系O-XYZ和TCP处局部坐标系xt，yt和zt。滚珠丝杆驱动主轴组件沿直线导轨运动以实现工作空间Z方向的位置变化。

从图1可以看出，整个机床被分为主轴和床身两个子结构，根据多结合部的刚度、阻尼、位移约束条件和受力平衡关系将子结构在工作空间的不同位置耦合，应用RCSA推导出耦合后TCP的FRFs表达式。

1.1 结合部简化模型

机床各子结构是以结合面(多节点连接)的形式传递作用力，各子结构的动力学建模独立进行，不仅存在结合面网格节点不统一的问题，甚至不同子结构的网格类型也不尽相同。为简化处理，将结合面的多个节点按照权重因子缩聚至一点[10]，以有效解决网格不兼容和节点错位等问题。如图1，假设点1，2，3，4为床身导轨与主轴滑块接触面的缩聚点，则点1'，2'，3'和4'为主轴子结构相应接触面的缩聚点（点1和1'属于一对结合部，以下类似）；点5和5'分别为滚珠丝杠副在床身和主轴接触面的缩聚点；点0为TCP位置；ki和ci分别为第i对接触副的刚度和阻尼。

1.2 子结构结合部频响函数的构建

主轴子结构是一个自由部件，0点为刀尖点，受切削激励作用，对主轴进行自由部件的模态分析，提取多阶固有频率及模态。床身对主轴动力性能的影响是通过结合部的耦合作用实现，子结构在多个结合部受位移和力耦合作用，如图1所示。考虑结合部的缩聚，主轴子结构TCP及5处结合部的原点频响hqq和跨点频响hpq可采用如下模态展开表示：

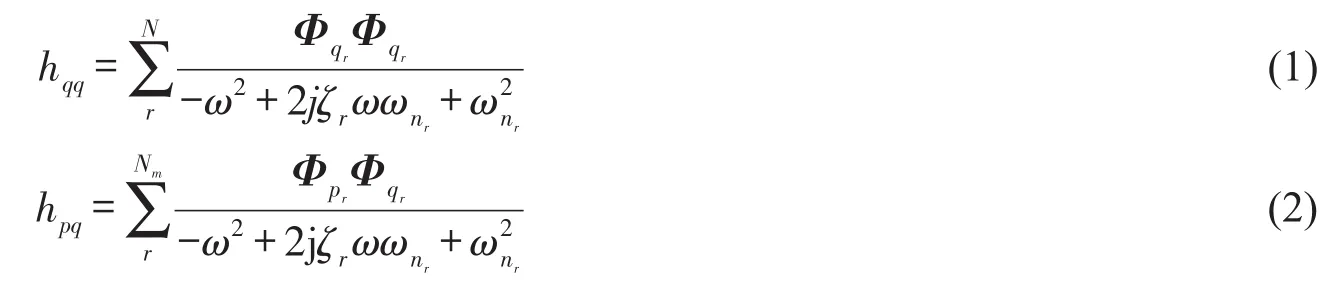
其中：ω为激励频率，Hz；Nm为子结构总模态数；ωnr为第r阶模态特征值,Hz；p为激励处缩聚点，q为响应处缩聚点，p≠q，p,q∈1,2,3,4,5；Φpr，Φqr分别为 p点和q点第r阶质量归一化特征向量；ζr为第r阶模态阻尼比；j是虚运算符。

综合式(1)，(2)得主轴子结构的频响函数矩阵H；床身子结构1'～5'的原点频响gqq和跨点频响gpq采用类似方法构建，组装成床身子结构的频响函数矩阵G。主轴和床身子结构的频响函数矩阵H、G均为对称阵。

1.3 基于RCSA的TCP频响函数综合

将主轴子结构频响函数矩阵H展开，得：

类似地，床身子结构1'～5'处的位移用各自的频响函数在频域内展开，结果如下：

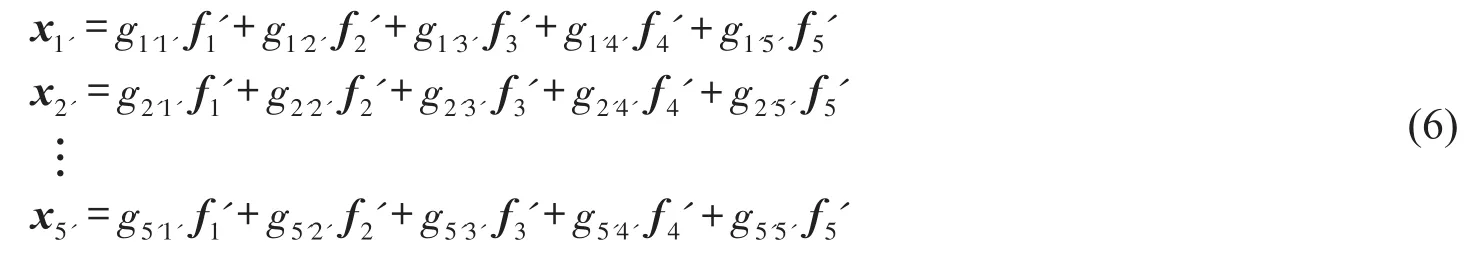
其中：f0为主轴子结构0处的切削激振力向量；x0～x5，f1～f5分别为主轴子结构缩聚点0～5处的位移向量和约束力向量；x1'～x5'，f1'～f5''分别为床身子结构点1'～5'的位移向量和约束力向量。根据作用力与反作用力关系，有

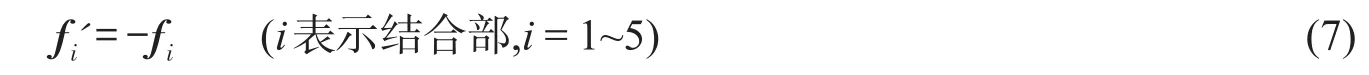
考虑结合部的刚度和阻尼（图1结合部耦合示意图），结合部应满足

其中Ki=ki+jwci，为第i结合部的等效复刚度矩阵。将式(6)～(8)代入式(5)，得到表达式如下：

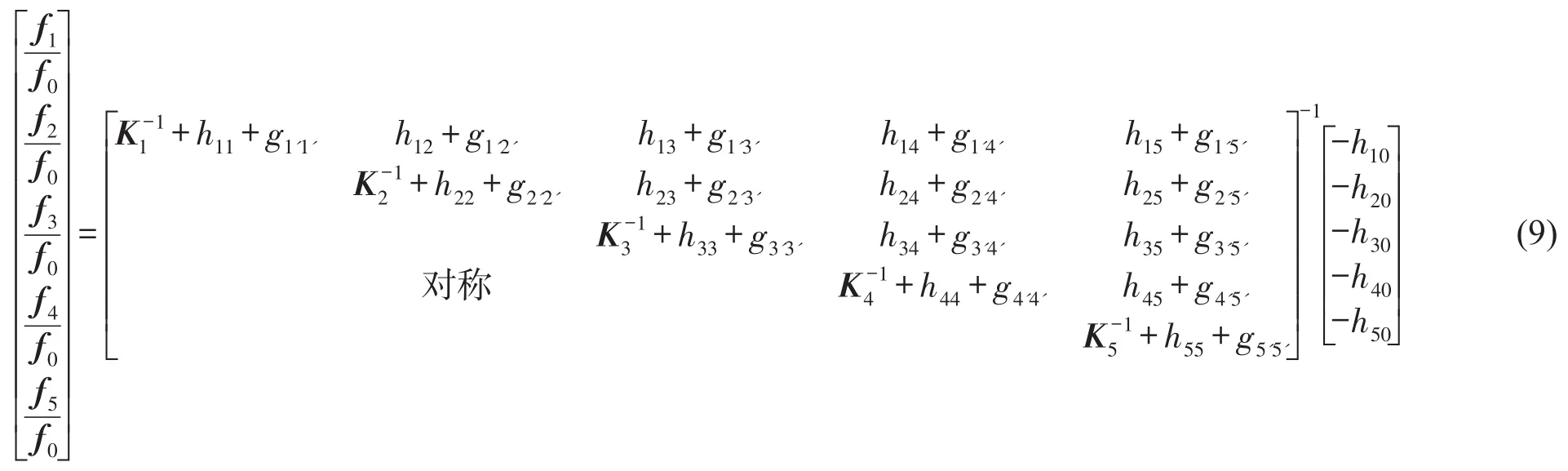
基于方程(5)，TCP的频率响应函数可由两子机构结合部的频响函数综合得

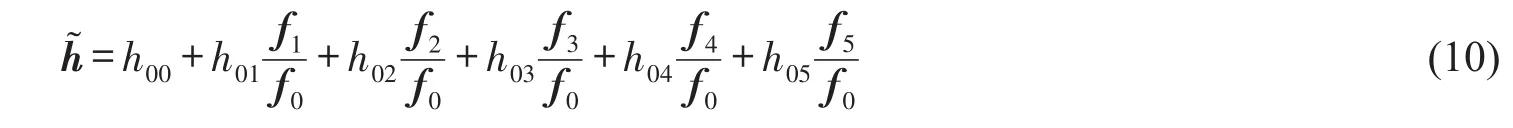
根据结合部约束力和变形协调关系，将方程(9)代入方程(10)，TCP的FRFs可表示为子机构的FRFs的矩阵运算，如

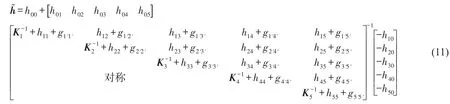
式(11)为由两个子结构(床身和主轴)的频响函数综合得到的整机TCP动态特性的统一表达式，可对TCP在不同加工位置处进行FRFs计算。

2 计算范例

以VDF850立式机床为算例，采用RCSA法研究机床TCP的动力学特性。

2.1 主轴和床身的频响函数矩阵

将VDF850立式机床分为床身和主轴两个子结构，如图1。采用有限单元法(finite element method，FEM)对机床床身和主轴进行动力学分析。各子结构均采用10节点实心四面体单元建模。各组件有限元模型的具体力学参数设置如表1。

表1 VDF850立式机床材料力学参数Tab.1 Mechanical parameters of VDF850 vertical machine tools

分别运用Ansys有限元软件对子结构的自由或约束模态进行分析和提取，将获得的各子结构模态参数导入Matlab，激励频率ω为0～2 000 Hz，离散间隔为5 Hz。各阶模态阻尼比统一设置为0.1，由式(1)，(2)得结合部缩聚点频响函数的离散数值解，并由式(3)，(4)组装得子结构的频响函数矩阵序列。

2.2 TCP频响函数综合

主轴子结构通过滚珠丝杠驱动滑块在导轨上移动来实现主轴在Z轴的不同加工位置。多结合部包括导轨结合部、丝杠螺母结合部及床身地面基础结合部，床身通过螺栓和地面基础固定。各结合部的参数设置为：滚珠丝杆结合面刚度系数kb=250 MN·m-1；阻尼系数cb=250 N·s·m-1；四处导轨结合面刚度系数相同，ks=50 MN·m-1；阻尼系数也相同，cs=500 N·s·m-1；床身与地面基础的刚度系数kr=250 MN·m-1；阻尼系数cr=250 N·s·m-1。将子结构的频响函数代入式(11)，在Matlab软件中进行矩阵运算可得TCP的FRFs。

图2为Z=500 mm，主轴处于顶部(Top)位置，TCP在xt，yt和zt3个正交方向上的频响函数。由图2可见，xt，yt方向频响函数基本相近，zt方向动柔度幅值较xt，yt小一个数量级，即zt方向动刚度远大于xt，yt两个方向，故铣削动力学建模中通常只考虑xt，yt两个正交方向[11]。

2.3 RCSA法的可行性验证

为验证RCSA法的可行性，采用整机有限元法建立VDF850立式机床的动力学模型[12]，当主轴处于顶部位置时，通过整机大规模动力学特征方程矩阵求解，计算TCP的频率响应函数。两种方法获得的TCPyt方向FRFs如图3。由图3可知：两方法所得TCP的动柔度幅值曲线基本一致；前三阶固有频率处RCSA法较整机有限元法幅值略偏高，这与结合面缩聚增大系统刚度有关。由此表明采用RCSA法对机床进行动力学分析是可行的。

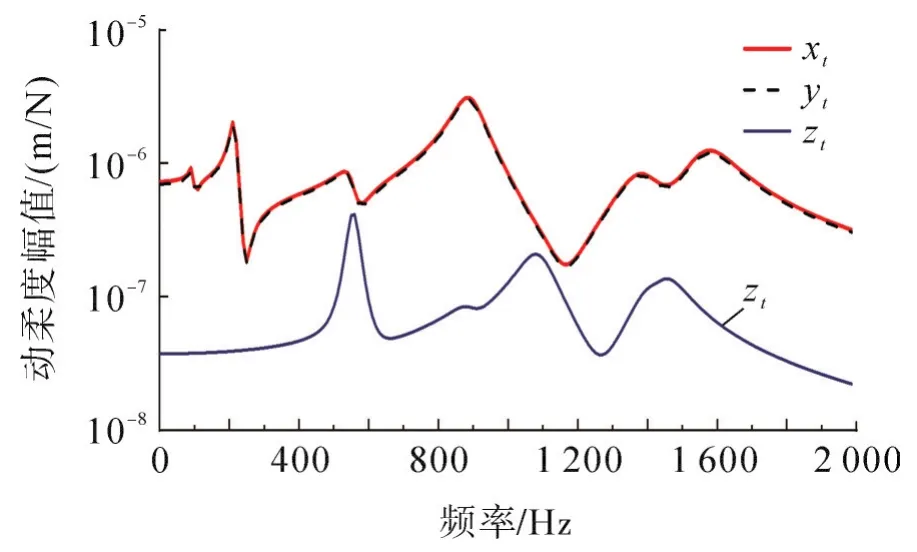
图2 TCP3个正交方向xt，yt和zt的FRFsFig.2 FRFs of TCP in three orthogonal directionsxt，ytandzt

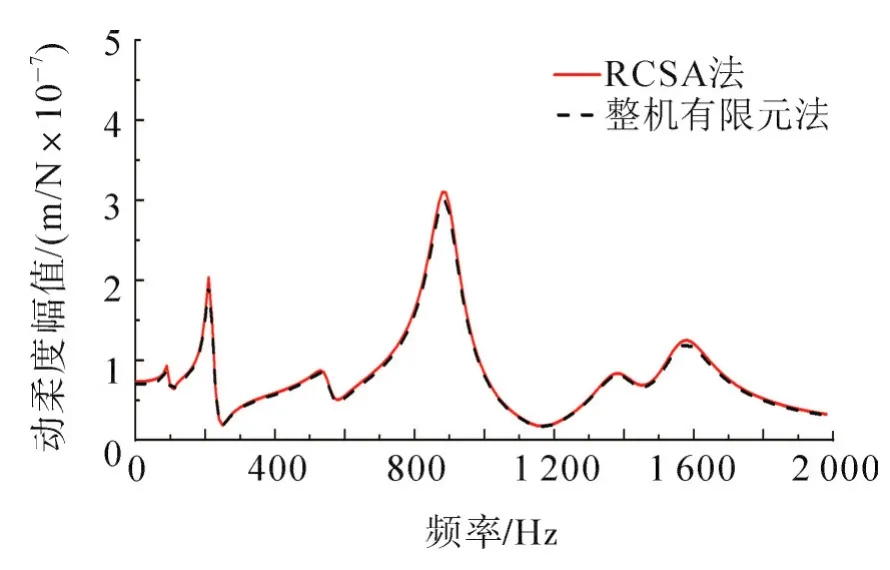
图3 TCP在yt方向FRFs对比Fig.3 Comparison of FRFs of TCPin theytdirection

当主轴位于不同位置，RCSA法只需计算5对结合部频响函数矩阵，采用式(11)的低阶矩阵运算即可获得TCP的频率响应函数，而整机有限元法则需对每个具体位置进行高阶动力学特征方程求解。故与整机有限元法相比，RCSA法计算效率有所提高。

2.4 Z方向维度TCP的动力学响应

VDF850机床主轴Z方向的运动范围为0～510 mm，图4为主轴在0～500 mm工作空间刀尖点yt方向动柔度幅值响应曲面。图5为主轴处于3个典型位置Top(Z=500 mm)，Middle(Z=250 mm)，Bottom(Z=0 mm)，刀尖点yt方向动柔度幅值响应。综合图4，5可得出：当主轴处于顶部(Top)的加工位置，各阶响应均最大，且在89 Hz处有一小峰值，随着主轴位置的下降，系统刚度增大，此处峰值消失；各阶固有频率对应动柔度幅值均随主轴下移而降低，但不同固有频率处的变化幅度不尽相同，文献[10-11]也得出类似的结论。

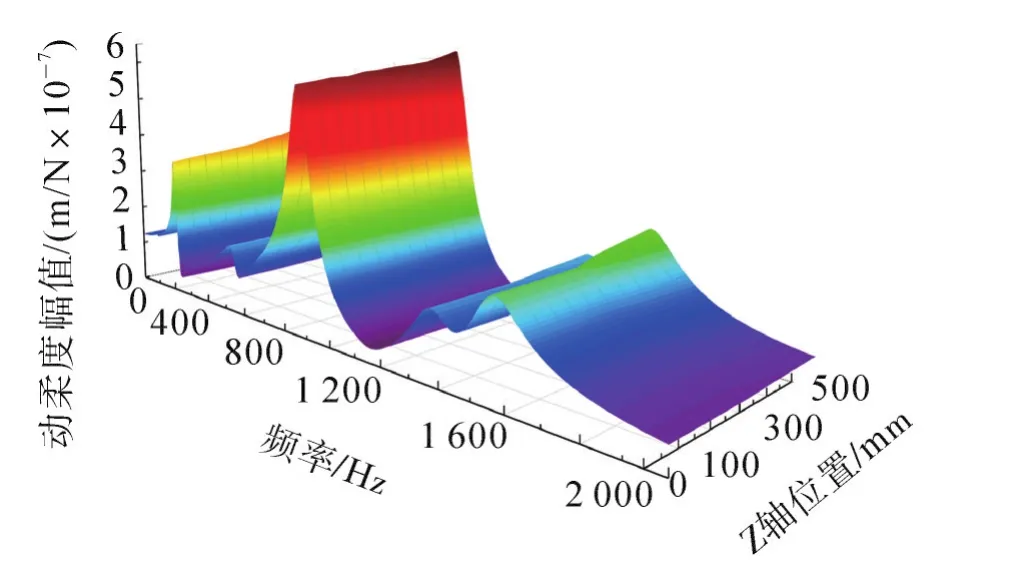
图4 yt方向TCP的FRFs与Z轴位置关系Fig.4 FRFs of TCP inytdirection varied with Zaxis position

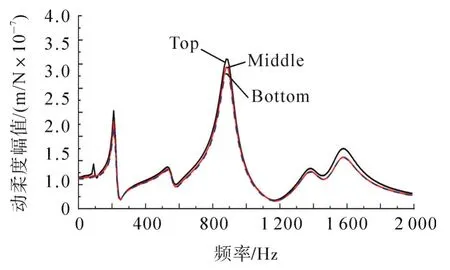
图5 3个典型位置处TCP在yt方向FRFsFig.5 FRFs of TCP inytdirection varied with Zaxis position

3 结 论

1)采用RCSA法建立机床的动力学模型，根据多结合部的变形协调关系及受力平衡条件给出了TCP的FRFs统一表达式。

2)以立式机床VDF850为算例，应用RCSA法计算TCP的FRFs，计算结果和整机有限元法基本一致，但RCSA法避免了整体动力矩阵的特征值重复计算，可提高计算效率。

3)立式机床VDF850在Z方向维度动力学响应变化的研究结果表明，各阶固有频率处动柔度幅值随主轴位置下降而降低，但不同固有频率处的变化幅度不尽相同。

文中仅针对TCP在工作空间Z方向维度的动力特性进行了探讨，对X，Y方向维度及其不同组合状态的动态特性有待进一步研究。后期研究获得的整个工作空间TCP频响与高速切削联合建模，可为开展高速切削稳定性研究提供理论支持。