支付值为梯形直觉模糊数的改进矩阵博弈求解方法

贾 磊， 谭睿璞

(福建江夏学院a.工程学院；b.电子信息科学学院， 福州 350108)

引 言

博弈论是研究具有斗争性和竞争性管理决策问题的理论和方法，广泛应用于经济学、政治学、心理学、生物学和军事战略等领域[1]。由于信息的不确定性、局中人的有限理性和决策行为的复杂性，局中人的判断存在一定的模糊性和不确定性。模糊博弈理论尤其是模糊矩阵博弈理论得到广泛研究[2-9]。然而，在实际博弈问题中，由于对策所涉及的信息不完全，且涉及到经济、政治、心理行为、意识形态等复杂因素，局中人的判断存在一定的犹豫程度。直觉模糊集[10]同时考虑了隶属、非隶属和犹豫度3方面信息，较好地刻画了各个局势下局中人判断的肯定、否定和犹豫程度3种状态信息，因此，直觉模糊博弈理论和方法成为研究热点[11-17]，包括支付值为直觉模糊集、三角直觉模糊数(TIFN)和梯形直觉模糊数(TrIFN)的博弈问题。

文献[11]研究支付值为直觉模糊集的矩阵博弈求解方法。Nan等[12]提出了基于三角直觉模糊数排序函数的双目标线性规划矩阵博弈求解方法。Nan等[13]提出了基于隶属度和非隶属度平均值排序函数的三角直觉模糊数矩阵博弈方法。Verma[14]对文献[13]建立的线性规划模型中的错误假设进行了研究。Seikh等[15]提出了支付值为三角直觉模糊数的双目标非线性规划求解方法。文献[16]提出基于差分指数排序函数和线性规划的梯形模糊数矩阵博弈求解方法。文献[17]定义了α-矩阵对策的概念，提出一种求解支付为梯形模糊数的矩阵对策的线性规划新方法。文献[18]提出基于加权可能性均值的直觉梯形模糊数矩阵博弈求解方法。

目前对支付值为直觉模糊数，特别是梯形直觉模糊数的博弈理论和方法研究较少。本文主要研究支付值为TrIFN的矩阵博弈问题及其线性规划求解方法，引入基于均值和模糊度的排序函数，在对现有文献分析的基础上，指出其不合理的地方，并构建改进的线性规划模型，最后通过实例说明算法的有效性。

1 基础理论

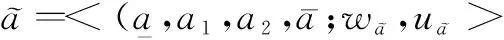
其中，

定义2[20]设

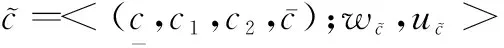
易证明上述运算法则具有如下性质：

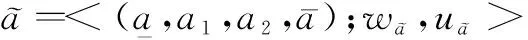
其中

0≤α+β≤1。根据TrIFN的定义可以得到：

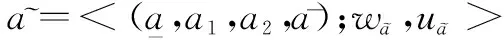
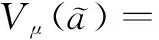
(3)

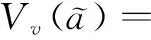
(4)

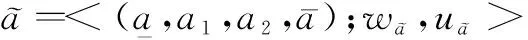
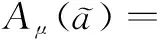
(5)

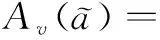
(6)

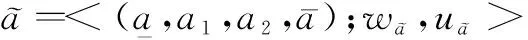
(7)

(8)

其中，λ∈[0,1]为局中人的一种偏好权重，λ∈[0.5,1]表明局中人喜欢肯定的或正面信息；λ∈[0,0.5]表明局中人喜欢否定的或负面信息；λ=0.5表明局中人持中立态度。

定义7设

是任意2个梯形直觉模糊数，λ∈[0,1]，则其大小关系或排序：

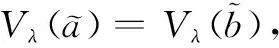
2 梯形直觉模糊数矩阵博弈模型的构建及求解

2.1 梯形直觉模糊数矩阵博弈模型构建

设局中人P1和P2的纯策略集合为S1={α1,α2,…,αm}和S2={β1,β2,…,βn}，混合策略空间为

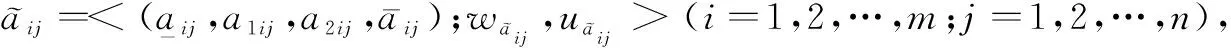
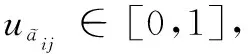
(9)

定义8[20]设

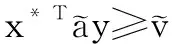
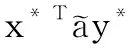
2.2 梯形直觉模糊数矩阵博弈求解

根据定义8和定义9可知，局中人P1和P2的最优策略(x*,y*)可分别通过求解下面一对带有梯形直觉模糊数的数学规划模型得到：

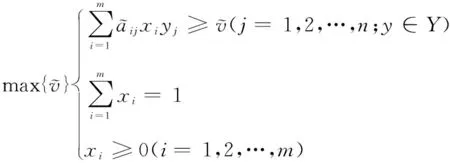
(10)

(11)

根据定义2，式(10)和式(11)分别转化为：

(12)

(13)

根据定义6的排序方法，式(12)和式(13)转化为：

(14)

(15)

根据式(7)和式(8)，式(14)转化为：

(16)

式(15)可做类似转化。

2.3 改进的梯形直觉模糊数矩阵博弈求解方法

通过分析式(14)、式(15)和式(16)，可发现文献[12,20]的模型中存在错误假定，其认为

而实际上它们并不相等。因为根据定义2的TrIFN运算法则及式(7)、式(8)可得：

(17)

(18)

易得

类似可得

受文献[14,16]的启发，为易于计算，令

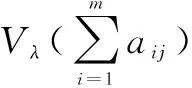
(19)

(20)

[λξ+(1-λ)k])

将式(19)和式(20)带入式(14)和式(15)，可得：

(21)

(22)

为计算简便，设：

则式(21)和式(22)可转化为：max{V1},min{A1}

(23)

min{V2},max{A2}

(24)

为求解，将式(23)和式(24)转化为线性规划模型：

max{V1}

(25)

和

min{V2}

(26)

进而根据式(23)和式(24)，分别构造线性规划模型，

min{A1}

(27)

和

max{A2}

(28)

3 实例分析

3.1 数值例子

其中<(50,60,70,80);0.8,0.1>表示当公司A和B都选择策略α1即增加广告宣传时，公司A的产品销售额为60万元～70万元之间，其最大隶属度为0.6，最小非隶属度为0.2，犹豫度为0.2。其它TrIFN可作类似解释。

步骤1计算：

步骤2将步骤1得到的ξ和k值带入式(25)，可得：

max{V1}s.t.

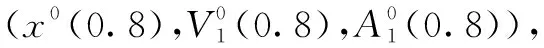
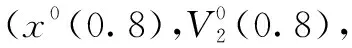
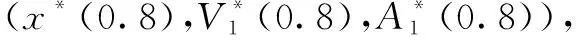
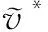
表1 不同λ取值时局中人的最优策略、加权均值、加权模糊度及博弈值

3.2 对比分析

为说明本文算法的正确性及合理性，将其与文献[20]中的方法进行比较分析，分别取不同λ值，两种方法的最优策略及相应的博弈值见表2。

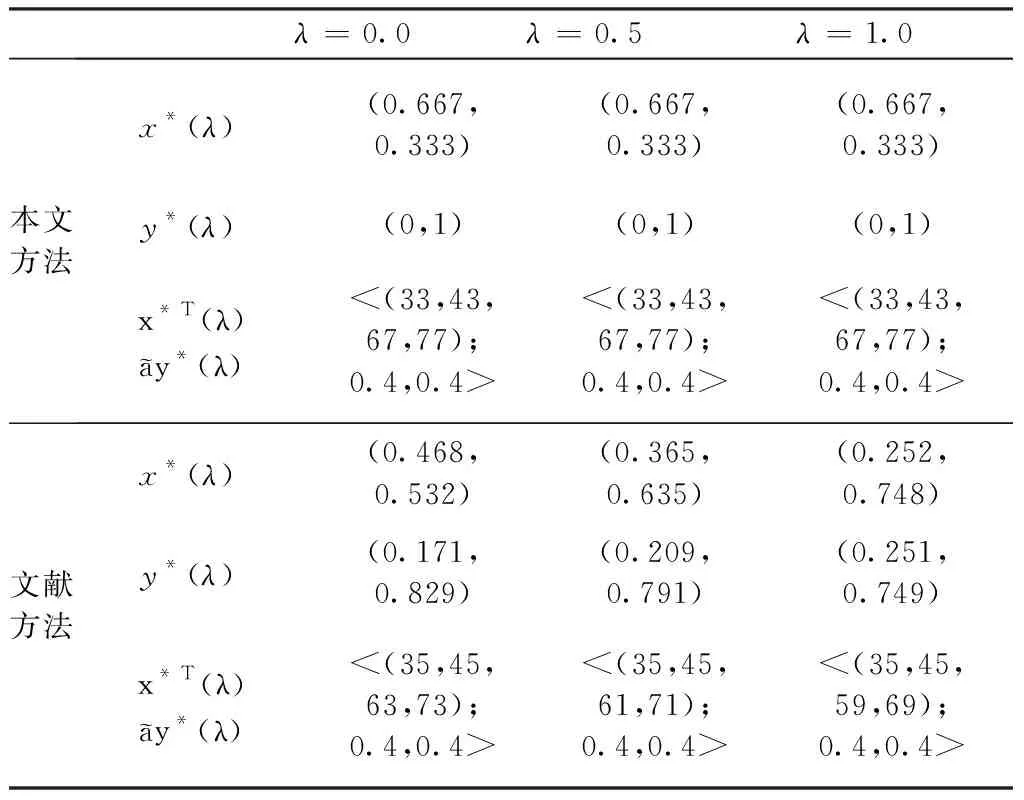
表2 不同λ取值时两种方法的最优策略及博弈值

由表2可知，采用本文方法得到的期望支付值<(33,43,67,77);0.4,0.4>不变，不受λ取值的影响，且与采用文献[20]方法得到的期望支付值大致相同。随着λ取值不同，采用文献[20]的方法得到的局中人的最优策略是不确定的，而采用本文方法得到的最优策略是稳定的。

4 结束语

本文研究了支付值为梯形直觉模糊数的矩阵博弈方法，引入了梯形直觉模糊数均值和模糊度的概念，并给出了基于加权均值模糊度排序方法的线性规划求解方法。提出了改进的矩阵博弈线性规划求解方法，并应用到市场产品销售博弈问题中，通过实例分析验证了该方法的有效性。本文的方法可拓展到其他具有类似的直觉模糊支付矩阵对策求解问题。在今后的工作中，将进一步对直觉模糊博弈理论和方法进行深入研究。

参考文献：

[1] NEUMANN J V,MORGENSTERN O.The Theory of Games and Economic Behavior[M].Princeton:Princeton University Press,1944.

[2] BECTOR C R,CHANDRA S,VIJAY V.Duality in linear programming with fuzzy parameters and matrix games with fuzzy payoffs[J].Fuzzy Sets and Systems,2004,146(2):253-269.

[3] BECTOR C R,CHANDRA S.Fuzzy mathematical programming and fuzzy matrix games[M].Berlin:Springer Verlag,2005.

[4] VIJAY V,MEHRA A,CHANDRA S,et al.Fuzzy matrix games via a fuzzy ralation approach[J].Fuzzy Optimization and Decision Making,2007,6(4):299-314.

[5] LI D F.An effective methodology for solving matrix games with fuzzy payoffs[J].IEEE Transactions on Cybernatics,2013,43(2):610-621.

[6] LI D F.A fast approach to compute fuzzy values of matrix games with payoffs of triangular fuzzy numbers[J].European Journal of Operational Research,2012,223:421-429.

[7] CEVIKEL A C,AHLATCIOGLU M.A linear Interactive solution concept for fuzzy multiobjective games[J].European Journal of Pure and Applied Mathematics,2010,3(1):107-117.

[8] KOCKEN H G,OZKOK B A,TIRYAKI F.A compensatory fuzzy approach to multi-objective linear transportation problem with fuzzy parameters[J].European Journal of Pure and Applied Mathematics,2014,7(3):369-386.

[9] SEIKH M R,NAYAK P K,PAL M.An alternative approach for solving fuzzy matrix games[J].International Journal of Mathematics and Soft Computing,2016,5(1):79-92.

[10] ATANASSOV K.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1986,20(1):87-96.

[11] 南江霞,安京京,汪亭,等.支付值为直觉模糊集的矩阵对策的线性规划求解方法[J].数学的实践与认识,2015,45(24):176-182.

[12] NAN J X,ZHANG M J,LI D F.A methodology for matrix games with payoffs of triangular intuitionistic fuzzy number[J].Journal of Intelligent & Fuzzy Systems,2014,26:2899-2912.

[13] NAN J X,LI D F,ZHANG M J.A lexicographic method for matrix games with payoffs of triangular intuitionistic fuzzy numbers[J].International Journal of Computational Intelligence Systems,2010,3(3):280-289.

[14] VERMA T,KUMAR A.A note on “A lexicographic method for matrix games with payoffs of triangular intuitionistic fuzzy numbers”[J].International Journal of Computational Intelligence Systems,2016,8(4):690-700.

[15] SEIKH M R,NAYAK P K,PAL M.Solving bi-matrix games with pay-offs of triangular intuitionistic fuzzy numbers[J].European Journal of Pure and Applied Mathematics,2015,8(2):153-171.

[16] VERMA T,KUMAR A,APPADOO S S.Modified difference-index based ranking bilinear programming approach to solving bimatrix games with payoffs of trapezoidal intuitionistic fuzzy numbers[J].Journal of Intelligent & Fuzzy Systems,2015,29:1607-1618.

[17] 杨洁,李登峰.求解梯形模糊矩阵对策的线性规划方法[J].控制与决策,2015,30(7):1219-1226.

[18] 万树平,张小路.基于加权可能性均值的直觉梯形模糊数矩阵博弈求解方法[J].控制与决策,2012,27(8):1121-1126,1132.

[19] LI D F.A note on “Using intuitionistic fuzzy sets for fault-tree analysis on printed circuit board assembly”[J].Microelectronics Reliability,2008,48(10):1741.

[20] 李登峰.直觉模糊集决策与对策分析方法[M].北京:国防工业出版社,2012.

[21] LI D F,YANG J.A difference-index based ranking bilinear programming approach to solving bimatrix games with payoffs of trapezoidal intuitionistic fuzzy numbers[J].Journal of Applied Mathematics,2013(3):1-10.

[22] 林友谅,李武,韩庆兰.直觉模糊数密度集成算子及其应用[J].控制与决策,2017,32(6):1026-1032.

[23] 安京京,李登峰,南江霞.直觉模糊数加权高度排序法[J].系统科学与数学,2017,37(9):1949-1959.

[24] 王蕊,于宪伟.基于新得分函数的直觉模糊多属性决策方法[J].模糊系统与数学,2016,30(4):102-106.