基于三参数Weibull分布的粘性泥石流一次总量计算模型

李 俊， 陈宁生， 赵苑迪

(1.四川理工学院土木工程学院， 四川 自贡 643000；2.中国科学院、水利部成都山地灾害与环境研究所， 成都 610041)

引 言

粘性泥石流是由宽级配土体构成的固液气三相流体，其运动过程多呈阵性流态，对具有阵性流态的粘性泥石流也称阵性泥石流[1-5]。这种高流速(4 m/s～8 m/s)、冲击力大和搬运固体物质能力强的泥石流对世界各地山区城镇、交通和矿山等极具威胁。例如1999年11月15～16日委内瑞拉Nianguaa城暴发了世界上规模最大的粘性泥石流，造成30000人死亡和严重的经济损失[6]。在中国西南山区，尤其是汶川地震、芦山地震和鲁甸地震后，多处暴发的粘性泥石流均对城镇、公路和矿山造成了严重的经济损失和人员伤亡[7-13]。为了减轻粘性泥石流危害，世界各地广泛采用了拦挡坝和排导槽等泥石流稳、拦、排防治工程。

粘性泥石流的一次总量是粘性泥石流稳、拦、排防治工程的重要设计参数，但该类泥石流一次总量的准确评估较为困难，尤其是具有阵性流态的粘性泥石流。有关粘性泥石流一次总量计算方法主要有三类，分别为直接观测测量法、经验公式和统计模型。这三类计算方法分别存在如下问题：(1)通过直接测量泥石流堆积区的固体物质得出一次泥石流总量的计算方法只适用于小规模、短历时和高阻力的泥石流沟，其最大缺陷是要求粘性泥石流搬运的固体物质全部堆积于堆积扇上。(2)一次泥石流总量经验公式主要有五边形法、泥石流防治工程勘查规范提供的方法和Crosta方法(表1)。五边形法和泥石流规范方法在计算粘性泥石流一次总量的过程中存在泥石流运动时间难以估计的问题，而Crosta方法只适用国外于局部山区。(3)根据蒋家沟粘性泥石流多年观测数据，陈宁生提出的基于峰值流量和运动时间的一次总量统计模型能够较好地计算粘性泥石流一次总量(表1)，但这种方法仍然存在2个问题[14]。第一，泥石流间断流历时大于3 min的流体视为两场泥石流，这使得某一场完整的粘性泥石流被人为分割，而且在实际应用中泥石流间断历时的调查十分困难。第二，该统计模型中稳定分位点流量与最大峰值流量的回归模型相关系数存在相关度不高的问题。(4)Donovan统计了美国西部的33次泥石流资料，提出了一种基于概率模型的泥石流总量计算方法，但该模型要求较多的计算参数，需要详细的泥石流基础资料才能计算一次泥石流总量[15]。大多数粘性泥石流都以阵性流的形式出现，由于阵性流存在较长时间的断流，因此粘性泥石流一次总量的直接观测测量法和经验公式法的应用受到限制，而且目前的统计模型尚有一定的不足。所以本文结合中国云南省东川县蒋家沟泥石流的阵性泥石流观测资料[16-17]，采用粒子群算法和三参数Weibull分布建立粘性泥石流一次总量的统计模型，以期为计算粘性泥石流一次总量提供精度更高的方法。

表1 粘性泥石流一次总量的计算模型

1 粘性泥石流特征及蒋家沟粘性泥石流数据处理

1.1 粘性泥石流的阵性特征

图1 粘性泥石流运动过程图

1.2 数据处理

蒋家沟位于中国云南省东川县，其流域面积48.6 km2。该沟粘性泥石流具有阵性特征，阵性流体过程完整。本文粘性泥石流中阵性流体的峰值流量和运动时间来源于1987～2004年蒋家沟126场现场观测的粘性泥石流数据。泥石流数据观测点设置在蒋家沟泥石流的顺直稳定沟段，设置上下两个断面，间距200 m(图2，改绘于文献[16])。泥石流运动时间为在观测点观测的阵性泥石流全部通过时间。泥石流峰值流量的计算参数为泥石流最大泥深、断面宽度和平均流速。泥石流的最大泥深根据UL-2型超声波泥位计自动测量。断面宽度为每次泥石流暴发前后测量的断面宽度平均值。泥石流流速根据粘性泥石流龙头通过间距为200 m的观测断面的时间确定。

图2 蒋家沟泥石流数据观测方法

在建立基于三参数Weibull分布的粘性泥石流一次总量计算模型前，根据下列原则整理了1987～2004年蒋家沟126场粘性泥石流数据：(1)只计阵性流体，扣除连续流体；(2)将符合条件(1)的阵性流体持续阵数大于或等于15次的一场泥石流数据全部选用，小于15次阵数的一场泥石流数据不采用，因为阵次数量较少的粘性泥石流不能反映流体总体特征。按以上原则，这126场粘性泥石流中的阵性流体数据都可以用于模型建立和模型验证。

2 方法

本文以云南省东川县蒋家沟1987～1996年73场粘性泥石流数据为统计基础，引入三参数Weibull分布描述阵性流量的分布特征，并采用粒子群算法计算阵性流量的Weibull分布参数。三参数Weibull分布是一种比两参数Weibull分布更为完善的概率分布，且三参数模式比两参数模式有更高的拟合精度。在拟合随机数据时三参数Weibull分布有很大的灵活性，对不同形状的频率分布有很强的适应性，当形状参数取不同值时，它可以等效或接近于正态分布或对数分布。在73场Weibull分布函数的基础上，采用指数回归模型确定最稳定分位点，即分位点流量与最大峰值流量回归方程相关度最高的分位点。基于最稳定分位点流量和三参数Weibull分布建立了基于三参数Weibull分布的粘性泥石流一次总量统计模型，其模型输入参数为最大峰值流量Qmax和泥石流运动时间TS，这两个参数在泥石流实际调查容易获取。最后根据蒋家沟1997～2004年53场粘性泥石流数据验证该模型的正确性，并比较该模型与目前已有模型的相对误差等。本文的技术路线如图3所示。

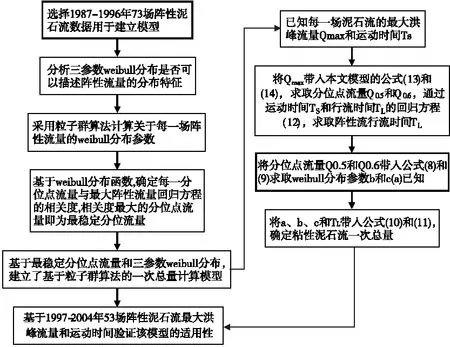
图3 基于三参数Weibull分布的一次总量统计模型建立流程图

2.1 最稳定Weibull分位点流量的粒子群算法

将1987～1996年每一场的阵性流量按数值大小进行分组，每一阵为一个频次，频数与每一场统计总次数的比值为频率。本文共统计了73场粘性泥石流的频率，并绘制了每一场不同规模的泥石流流量与频率的曲线，如图4所示。这73场的流量和频率曲线共有两种分布，一种呈负偏，共65场次，一种呈正偏态或对称分布，共8场次。各种分布和泥石流流量与频率曲线吻合度的分析结果显示Weibull分布更能反映泥石流流量的分布特征，三参数Weibull分布比二参数Weibull分布在描述正偏态、负偏态和对称分布等方面更加具有自由度高和可塑性大的优点[22-24]，所以引入三参数Weibull分布描述这73场阵性泥石流流量分布，三参数Weibull分布的概率密度函数为：

(1)

式中，x为阵性泥石流流量，m3/s；a为位置参数；b为尺度参数；c为形状参数；且b>0，c>0。

图4 阵性泥石流流量-频数曲线图

Weibull分布的三参数可通过粒子群算法准确求解。该算法是一类基于群体智能的算法。Weibull分布三参数计算：

(2)

(3)

式中，i=1,2,…,n。令初始粒子的位置为：

(4)

式中，N为粒子个数。将X1带入公式(4)得：

(5)

(6)

令Qm、Qn是一次泥石流流量过程线上的最稳定m、n分位点流量，且这两个分位点流量和阵性流体的最大值峰值流量具有最高的指数回归模型相关度。在获取每一场泥石流的a′、b′、c′值后，可求出0～1分位点对应的分位点流量，并拟合各分位点流量与每一场阵性流体的峰值流量最大值的回归方程，寻找这73个回归方程的最大相关度，相关度最大的两个分位点即为最稳定的两个分位点。指数回归方程的表达式：

(7)

式中，Qf为某分位点对应的分位点流量，m3/s；Qmax为每一场阵性流体的峰值流量最大值；D、E、F为回归模型参数。

2.2 基于三参数Weibull分布的一次总量计算模型

将1987～1996年每一场阵性泥石流的最大流量带入公式(7)，得出两个最稳定分位点流量，将这两个分位点流量带入式(8)和式(9)，得出Weibull分布的b值和c值，粒子群算法的计算结果显示75场的a值均为-2500。

(8)

(9)

(10)

一场粘性泥石流的一次总量计算公式：

(11)

R2=0.56

(12)

3 最稳定分位点计算结果与模型验证

3.1 最稳定分位点

基于粒子群算法计算结果，一次总量模型的最稳定三参数Weibull分位点为50%和60%，这两个分位点的阵性流量和最大阵流流量的回归曲线如图5所示，其回归方程分别如公式(13)和公式(14)所示。

图5 最稳定分位点流量和最大阵流流量的指数回归方程

(13)

(14)

由图5可知，50%和60%分位点流量与最大阵流流量的相关度均大于0.77，这说明50%和60%分位点流量与最大洪峰流量Qmax具有良好的相关性。

3.2 模型验证

模型验证的数据来源于蒋家沟1997～2004年53场粘性泥石流的最大洪峰流量、泥石流运动时间和实际泥石流总量(表2)。根据本文模型(式11)、陈宁生模型、泥石流规范方法、Crosta模型计算得出粘性泥石流的一次总量，并比较各种方法的相对误差、最大误差和均方根误差(表3)，相对误差Er和均方根误差RMSE公式为：

(15)

(16)

式中，Wc为模型计算的一次总量，m3；W为实际粘性泥石流总量，m3；N为粘性泥石流场次总数。

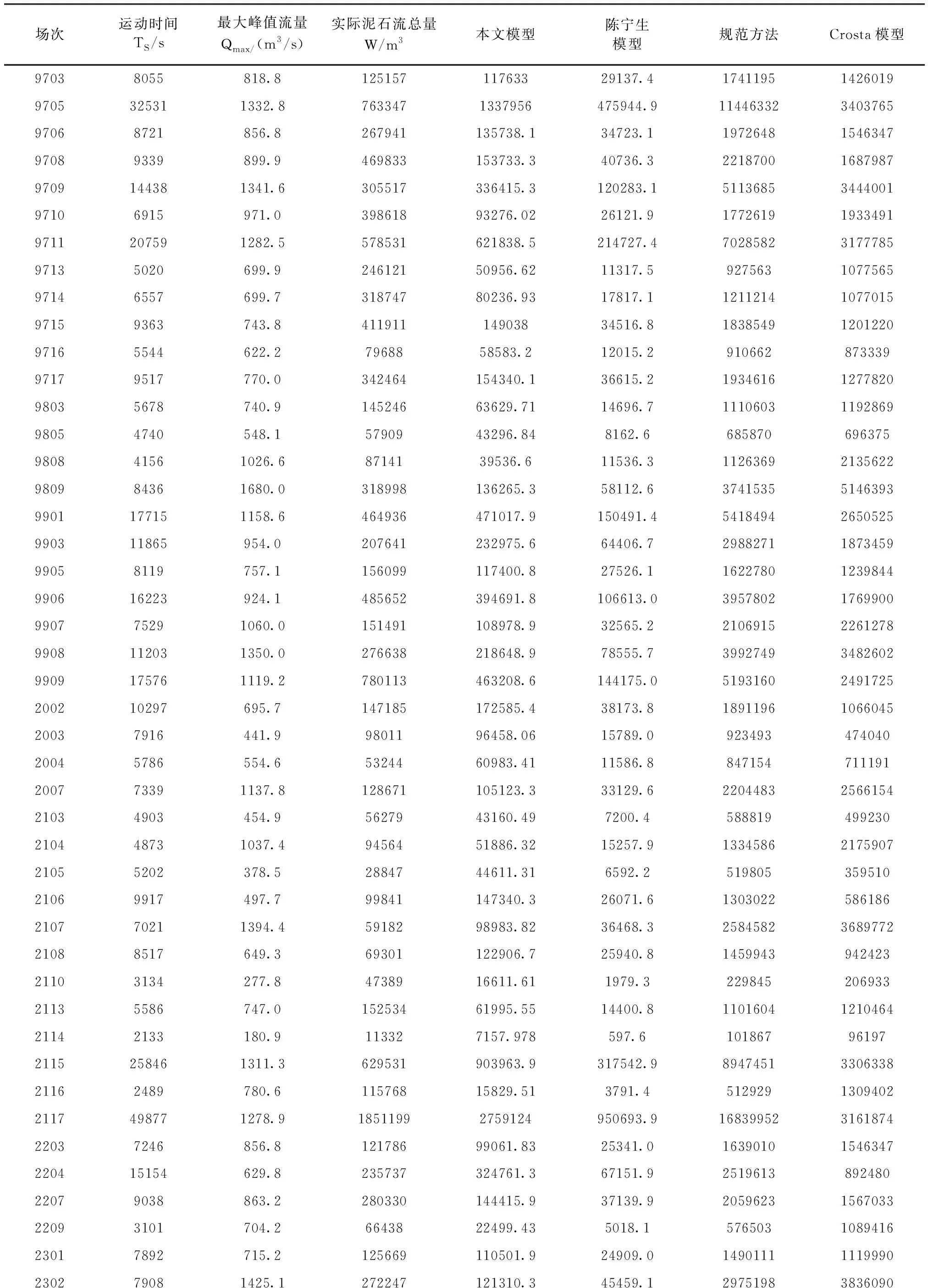
表2 模型验证数据

表3 各方法一次总量计算模型的相对误差、最大误差和均方根误差

由表3可知，基于三参数Weibull分布的一次总量模型相对误差、最大误差最小，分别为44.24%、89.08%。该模型的相对误差比陈宁生模型的相对误差降低29.62%，比泥石流规范方法的相对误差降低105.91%，这表明基于三参数Weibull分布的粘性泥石流一次总量模型具有更好地适用性。另外该模型的均方根误差比其他方法的均方根误差更小，这说明该模型计算的一次总量的离散度更低。

4 结 论

根据以上研究，得出以下三方面的结论：

(1)在蒋家沟粘性泥石流观测数据中，基于三参数Weibull分布的粘性泥石流一次总量统计模型的相对误差、最大误差、均方根误差，分别为44.24%、89.08%、21.21×104m3，该模型比陈宁生模型的相对误差低29.62%，比泥石流规范方法的相对误差低105.91%。说明基于三参数Weibull分布的一次总量计算方法适用于计算蒋家沟粘性泥石流一次总量。

(2)蒋家沟粘性泥石流的阵性流量较好地服从三参数Weibull分布，因而本文采用该法描述阵性流量的分布特征，这为建立基于三参数Weibull分布的一次总量模型奠定了基础。

(3)通过粒子群算法，求取了每一场泥石流Weibull分布的三参数，并寻求了最相关的分位点流量和最大峰值流量Qmax的回归方程。另外基于1987～1996年粘性泥石流数据，建立泥石流运动时间TS和阵性流体行流时间TL的幂函数回归方程。

参考文献：

[1] 康志成,李焯芬,马蔼乃,等.中国泥石流研究[M].北京:科学出版社,2004.

[2] 王兆印.泥石流龙头运动的实验研究及能量理论[C]//中国水利学会2001学术年会论文集.2001:18-26.

[3] 陈宁生,刘美,刘丽红,等.小流域中-低频泥石流与山洪输沙比例的讨论:以金沙江支流海子沟为例[J].成都理工大学学报:自然科学版,2017,44(2):225-231.

[4] 李俊,陈宁生,欧阳朝军,等.扎木弄沟滑坡型泥石流物源及堵河溃坝可能性分析[J].灾害学,2017,32(1):80-84.

[5] 许强,李骅锦,何雨森,等.文家沟泥石流治理工程效果的定量分析评价[J].工程地质学报,2017(4):1046-1056.

[6] REINALDO G M,JOSé L L.Debris flows of December 1999 in Venezuela[M].Heidelberg:Springer,2005.

[7] 崔鹏,陈晓清,张建强,等.“4·20”芦山7.0级地震次生山地灾害活动特征与趋势[J].山地学报,2013,31(3):257-265.

[8] 崔鹏,庄建琦,陈兴长,等.汶川地震区震后泥石流活动特征与防治对策[J].四川大学学报:工程科学版,2010,42(5):10-19.

[9] 郭晓军,苏鹏程,崔鹏,等.7月3日茂县棉簇沟特大泥石流成因和特征分析[J].水利学报,2012(S2):140-146.

[10] 屈永平,唐川,卜祥航,等.石棉县熊家沟“7·04”泥石流堵江调查与分析[J].水利学报,2016,47(1):44-53.

[11] 屈永平,唐川,刘洋,等.四川省都江堰市龙池地区“8·13”泥石流堆积扇调查和分析[J].水利学报,2015,46(2):197-207.

[12] 余斌,马煜,张健楠,等.汶川地震后四川省都江堰市龙池镇群发泥石流灾害[J].山地学报,2011,29(6):738-746.

[13] 舒志乐,史宝宁,张德宇.色多沟泥石流动力特征及危险性评估研究[J].四川理工学院学报:自然科学版,2016,29(6):70-74.

[14] LI J,CHEN N,WANG T,et al.A model for total volume of debris flow with intermittent surges based on maximum peak discharge and movement time[J].Geosystem Engineering,2016,20(4):1-14.

[15] DONOVAN I P,SANTI P M.A probabilistic approach to post-wildfire debris-flow volume modeling[J].Landslides,2017,14(4):1-16.

[16] 康志成,崔鹏,韦方强,等.中国科学院东川泥石流观测研究站观测实验资料集[M].北京:科学出版社,2006.

[17] 张军,熊刚.云南蒋家沟泥石流观测资料集(1987-1994)[M].北京:科学出版社,1997.

[18] JOHN E C,ROBERT L S.The formation and failure of natural dams[J].Geological Society of America Bulletin,1988,100(7):1054-1068.

[19] 周必凡.泥石流防治指南[M].北京:科学出版社,1991.

[20] DZ/TO239,泥石流灾害防治工程勘查规范[S].

[21] Chen NS,Yang CL,Zhou W,et al.A new total volume model of debris flows with intermittent surges:based on the observations at Jiangjia Valley,southwest China[J].Natural Hazards,2011,56(1):37-57.

[22] 张文明,董增川,朱成涛,等.基于粒子群算法的水文模型参数多目标优化研究[J].水利学报,2008,39(5):528-534.

[23] 金良琼.两参数Weibull分布的参数估计[D].昆明:云南大学,2010.

[24] 董胜,韩意,陶山山,等.Weibull分布参数的粒子群算法估计[J].中国海洋大学学报:自然科学版,2012,42(6):120-125.