模拟常减压蒸馏装置的物性计算方法和模型结构

郑 文 刚

(中国石油化工股份有限公司炼油事业部，北京 100728)

随着计算机软硬件技术的高速发展，流程模拟技术已逐渐被大专院校、研究设计单位、企业各级管理部门及工艺工程师所掌握。中国石油化工股份有限公司自21世纪初开始在各下属企业推广和应用该技术，培养了一批能熟练掌握和使用该技术的工程技术人员。目前流程模拟技术已在炼油厂装置设计、工况分析、故障诊断、挖潜增效、加工方案优化等方面发挥了重要作用，取得了显著的经济效益。

1 常减压蒸馏装置流程模拟

长期以来，在初馏塔、常压塔的塔盘效率估算，初馏塔、常压塔和减压塔进料压力、压降估算，减压炉转油线、汽化段、减压塔填料等板高度估算，重油的气液平衡预测等方面一直存在问题，加上现场原油评价、物料流量、温度、压力、分析数据等都存在一定误差，因此难以准确模拟常减压蒸馏装置。常减压蒸馏装置是炼油厂的“龙头”，其稳定和优化运行对全厂效益具有重要影响，因此有必要建立较准确的模型，指导该装置的设计、操作和优化。

2 常减压蒸馏装置模型结构

(1)总体思路。采用Aspen Plus V10.1软件，应用联立方程(Equation Oriented，简称EO)建模法建立某炼油厂的常减压蒸馏装置模型，然后选用不同的物性计算方法，建立特殊的减压部分模型结构，调用动态矩阵求解器(DMO)，在数据整定(Reconciliation)模式下求优，使得模拟计算结果与标定数据的误差平方和最小。把各种物性计算方法求得的最小误差平方和按从小到大排列，得出误差最小的物性计算方法。该方法的优点是能把原始标定数据的误差对模拟计算值的影响降低到最小程度，缺点是建模过程较复杂。

(2)塔盘效率。为了能使模型中的塔盘和实际塔盘一一对应，初馏塔和常压塔均采用实际塔盘进行建模，塔盘效率采用Murphree效率，其最优估计值采用EO建模法，用DMO求解器在Reconciliation求优模式下求解得到。减压塔塔盘数采用填料高度等板高度(HETP)折算成理论塔板数，由于填料的HETP也和气液相负荷有关，所以按填料的设计HETP计算出理论塔板数后，还需要进一步设置理论塔盘的Murphree效率。

(3)初馏塔、常压塔和减压塔塔顶气。一般情况下，模型预测的初馏塔、常压塔塔顶气流量均偏小，为了准确模拟初馏塔和常压塔塔顶瓦斯流量、回流罐温度，需要在初馏塔和常压塔进料中各添加一股气体，其组成和流量采用标定数据。在EO建模法中，可以对这两股气体流量进行数据整定，求解出最优流量估计值。

减压塔塔顶气一般流量很小，即使不做任何处理，通过模型也能准确模拟减顶气的温度和流量。

(4)初馏塔、常压塔、减压塔进料压力、全塔压降估算。采用与塔盘效率估算相同的方法，即采用EO建模法中的数据整定模式求出最优估算值。

(5)减压部分特殊的模型结构。减压炉转油线在进减压塔的汽化段前，因为压力不断降低，部分液相汽化吸热以及转油线散热导致温度降低。由于转油线直径较大，液相停留在下部，气相充满上部，且两相速度不一致，因此液相和气相难以达到相平衡，造成气相温度高，液相温度低。从减压炉出口气液两相呈相平衡状态到减压塔汽化段入口气液两相呈不平衡状态的过程中，存在某个压力，在该压力下，气相和液相完成相分离，建模时应把气相单独进洗涤段，液相进汽化段。计算表明，这种建模方法更准确，同时建模时也需考虑在汽化段闪蒸过程中存在雾沫夹带现象。如果不考虑该因素，减四线残炭和金属含量明显偏低。如减四线残炭实际值为4%～14%，主要集中在7%～10%，而模拟计算值往往小于5%。建模时，可把减压塔分成汽化段、汽化段以上、汽化段以下三部分考虑，对汽化段应考虑部分雾沫夹带[1-4]。

(6)序贯模块法(SM)和联立方程法(EO)。SM法沿着流程图走向，对单元设备逐个求解。遇到有循环的流量，则先设置物流初值，下游单元完成计算后，把循环物流计算值赋值给上次初始值，如此迭代，直到流程图全部收敛。EO法把系统的所有单元设备的物料、能量平衡方程、约束方程、变量连接方程、边界条件一起放在一个大型稀疏矩阵中，采用序贯二次型(SQP)法求解非线性方程组，从而得到流程图中所有单元设备的物料和能量流股信息。EO法求解速率快，不仅能求解设计问题，也能求解优化问题，还能给出参数的最优估计值。但该方法需要较大的计算机内存，且模型不收敛时不易查找问题[5]。

(7)换热网络。本课题目的是给出相对准确的物性计算方法用于常减压蒸馏装置模拟，换热网络影响不大，因此简化了换热网络。模型中初馏塔、常压塔和减压塔的进料温度固定。

(8)物性计算方法选用。物性计算方法是指一组热力学、传递性质计算模型，不是专指热力学状态方程(EOS)，EOS只是其中的一部分。如Maxwell-Bonnell[6]物性计算方法，气液平衡常数用Maxwell-Bonnell关联式计算，气体和液体的焓、熵、Gibbs自由能、气体和液体的摩尔体积用Soave-Redlich-Kwong[7]热力学状态方程计算。在Aspen Plus中物性计算方法统称为性质模型。由于不涉及换热网络、塔盘水力学核算、吸附分离、催化反应等，因此不讨论这些模型。

对于常减压蒸馏装置，特别是减压塔，各种物性方法的模拟结果差别较大。在实践中，经常遇到减压渣油的模拟收率和实际标定值有差距，一般偏低。最大的可能是减压部分没有选择合适的物性计算方法。以下探讨在Aspen Plus中用于常减压蒸馏装置模拟的准确物性计算方法。

在Aspen Plus中选用不同的物性计算方法对某常减压蒸馏装置进行模拟。其中初馏塔和常压塔选用一种方法，减压部分(含减压炉、减压塔)选用另一种方法，并在BK10[8]、Maxwell-Bonnell(简称MX)、Chao-Seader[9](简称CS)、Grayson-Streed[10](简称GS)、PENG-ROB或Peng-Robinson[11](简称PR)、Redlich-Kwong-SOAVE(简称RKS)、Soave-Redlich-Kwong (简称SRK)模型之间进行组合。

BK10和MX法属于蒸气压-液相逸度模型，CS和GS法属于气相状态方程-液相活度系数模型，PR、RKS和SRK法属于状态方程模型。这些方法都是一系列模型的组合，比如MX方法使用理想气体状态方程计算气相逸度系数，Maxwell-Bonnell关联公式计算饱和蒸气压，从而得到气液平衡常数、Soave-Redlich-Kwong方程计算气体和液体的焓、熵、Gibbs自由能、气体和液体的摩尔体积。

3 EO建模法下Aspen Plus不同物性计算方法对常减压蒸馏装置模拟结果的影响

任意挑选一套某炼油厂的常减压蒸馏装置标定数据，含原油评价、主要操作参数、物料平衡和产品分析数据。用Aspen Plus的EO建模法，建立了该装置的模型。

不仅物性计算方法会影响模拟结果，原油评价数据、塔盘效率、进料压力、塔压降、流量误差、温度误差、分析误差等也会影响模拟结果。为了严格比较物性计算方法的影响，需要剔除干挠因素或将其影响控制在最小范围内。因而采用如下方法：选定物性计算方法后，在数据整定模式下对模拟结果与标定数据的误差平方和求最小值。把多个物性计算方法对应的目标函数从小到大排列，就可得出最准确的方法。

以初馏塔为例，原油中的水分、进料压力、塔压降、塔盘效率、塔顶石脑油流量、塔顶气体流量是自变量。初馏塔塔顶石脑油干点、回流罐温度、塔底温度和塔顶回流量是因变量。这些变量除塔盘效率外，都存在测量值。在EO建模法的Reconciliation求解模式下，把关键变量的实测值和模拟值的误差平方和作为目标函数。并在装置各种约束范围内，求目标函数(OF)的最小值。

(1)

式中：Xim为某变量的实测值；Xis为该变量的模拟值；i为标准偏差。

建立的EO模型，自由变量总数是33个，目标函数中有37个关键变量，其中13个属于自由变量。模型的收敛时间为500～1 500 s，大部分情况下在1 200 s之内可收敛求得优解。不同物性方法组合对常减压蒸馏装置模拟结果的影响见表1。

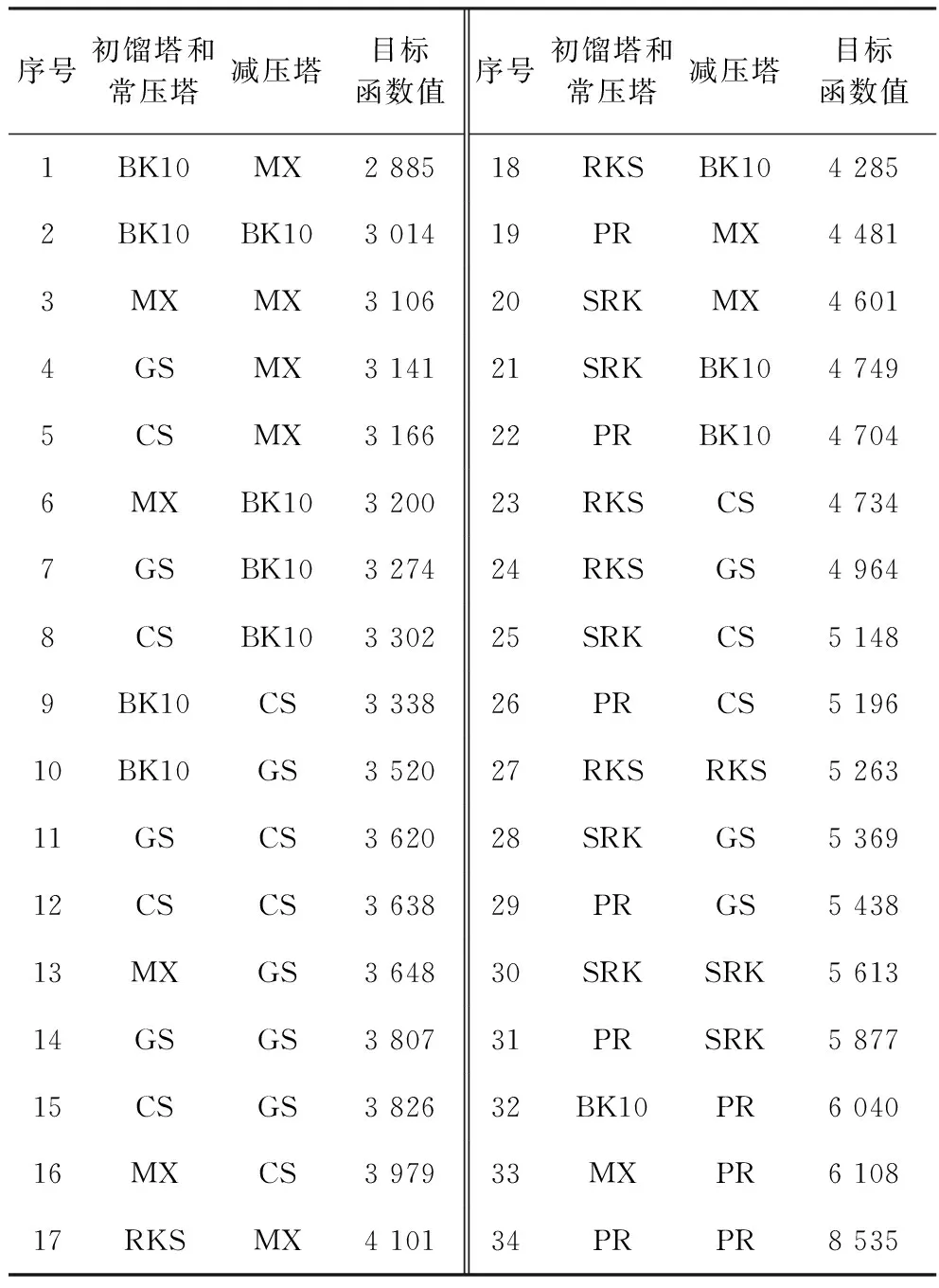
表1 Aspen Plus不同物性计算方法组合对常减压蒸馏装置模拟结果的影响

从表1可见，误差平方和最小的模型是初馏塔、常压塔部分用BK10，减压部分用Maxwell-Bonnell方法。(BK10+BK10)方法的误差是(BK10+MX)方法的1.05倍，(PR+PR)方法的误差是(BK10+MX)方法的2.96倍。可见用正确选用物性计算方法对于常减压蒸馏装置的模拟十分重要。从表1还可以看出，初馏塔和常压塔部分的物性计算方法按BK10，MX，GS，CS，RKS，SRK，PR的顺序，误差逐渐递增；减压部分的物性计算方法按MX，BK10，CS，GS，RKS，SRK，PR的顺序，误差逐渐递增；物性计算方法的使用范围越宽，如RKS、SRK和PR，准确度越低；方法的针对性越强，准确度就越高；越是有物理意义的模型，如PR，不如回归模型准确，如MX方法适于低压下的重组分(尤其适合减压深拔)，因此模拟减压部分越准；CS和GS法的差别较小，只是在液相的活度系数、Gibbs自由能和熵计算方法上有区别。

以下分初馏塔、常压塔和减压塔三部分，从表1的34组方法中挑选出最重要的方法组合，分析其对初馏塔、常压塔、减压塔模拟结果的具体影响，结果分别见表2、表3和表4。表中所列物性计算方法，如PR MX表示初馏塔和常压塔用Peng-Robinson方法，减压塔用Maxwell Bonnell方法。

由表2可见，初馏塔的进料压力误差较大，初馏塔的塔盘效率在70%左右，各方法对初馏塔均能较准确模拟，差别不大。

由表3可见，常压塔塔顶循环抽出温度、一中段抽出温度、塔顶冷回流量、塔顶石脑油、常一线、二线和三线流量模型预测值和实际有偏差，特别是冷回流和常一线流量。由于采样时间不同步等原因，实际化验分析数据可能不具有代表性。如提高常一线终馏点，常一线流量模拟值将增加，常二线流量将减小，计算值和标定数据将更为接近。上述结果也表明炼油厂的标定数据不完全是可信的，在EO建模法下，可以鉴别数据的合理性。

从表4可见，MX和BK10模型对于预测减压渣油、减四线流量较准确，MX模型更为准确，这与表1结果相符。模型预测结果表明，汽化段有2%～5%雾沫夹带量，这对于减四线性质模拟的准确性有较大帮助。同时是否考虑转油线的相分离对于减压塔模拟的准确度也有明显影响。

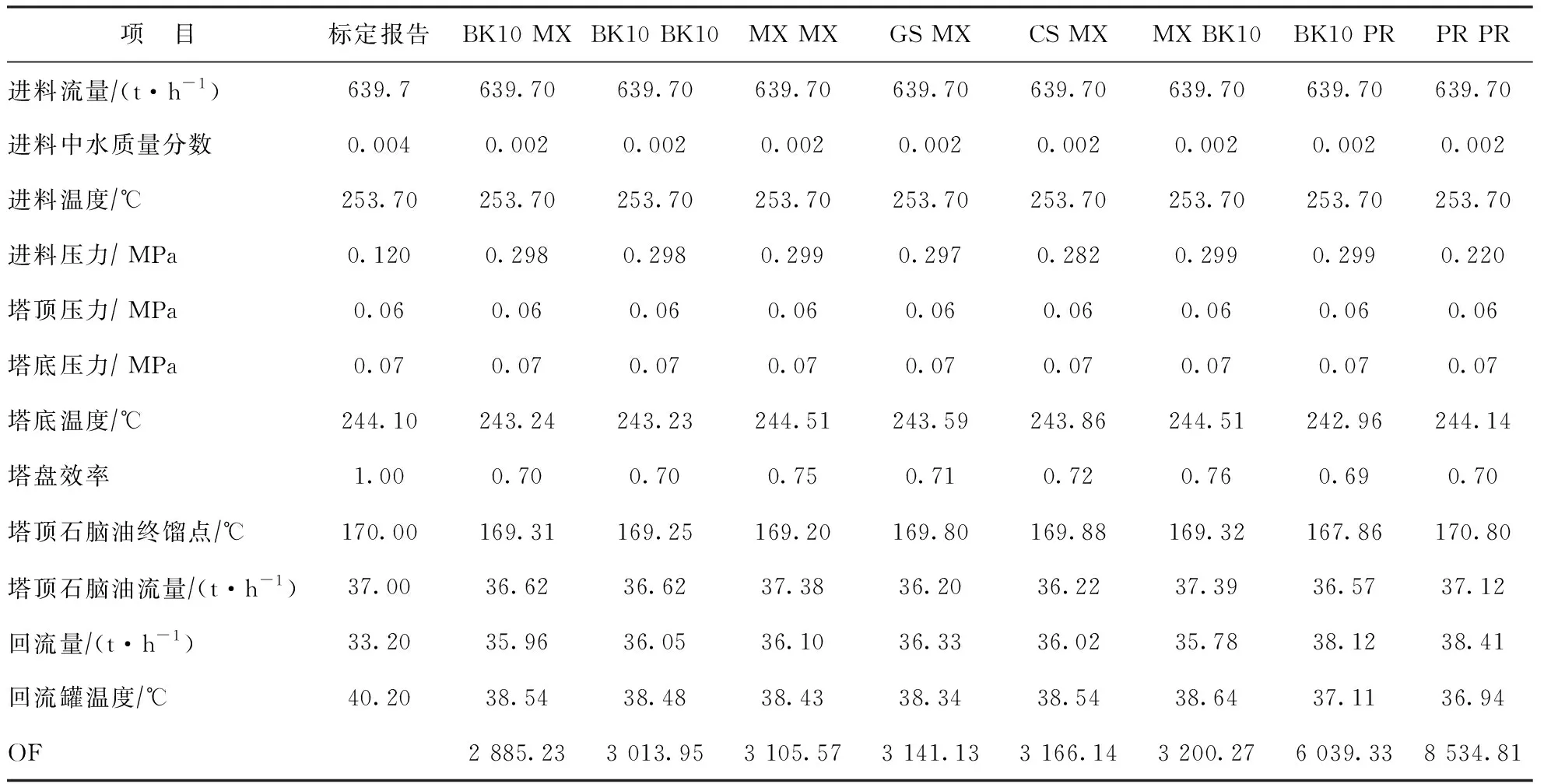
表2 不同物性计算方法对初馏塔模拟结果的影响

表3 不同物性计算方法对常压塔模拟结果的影响

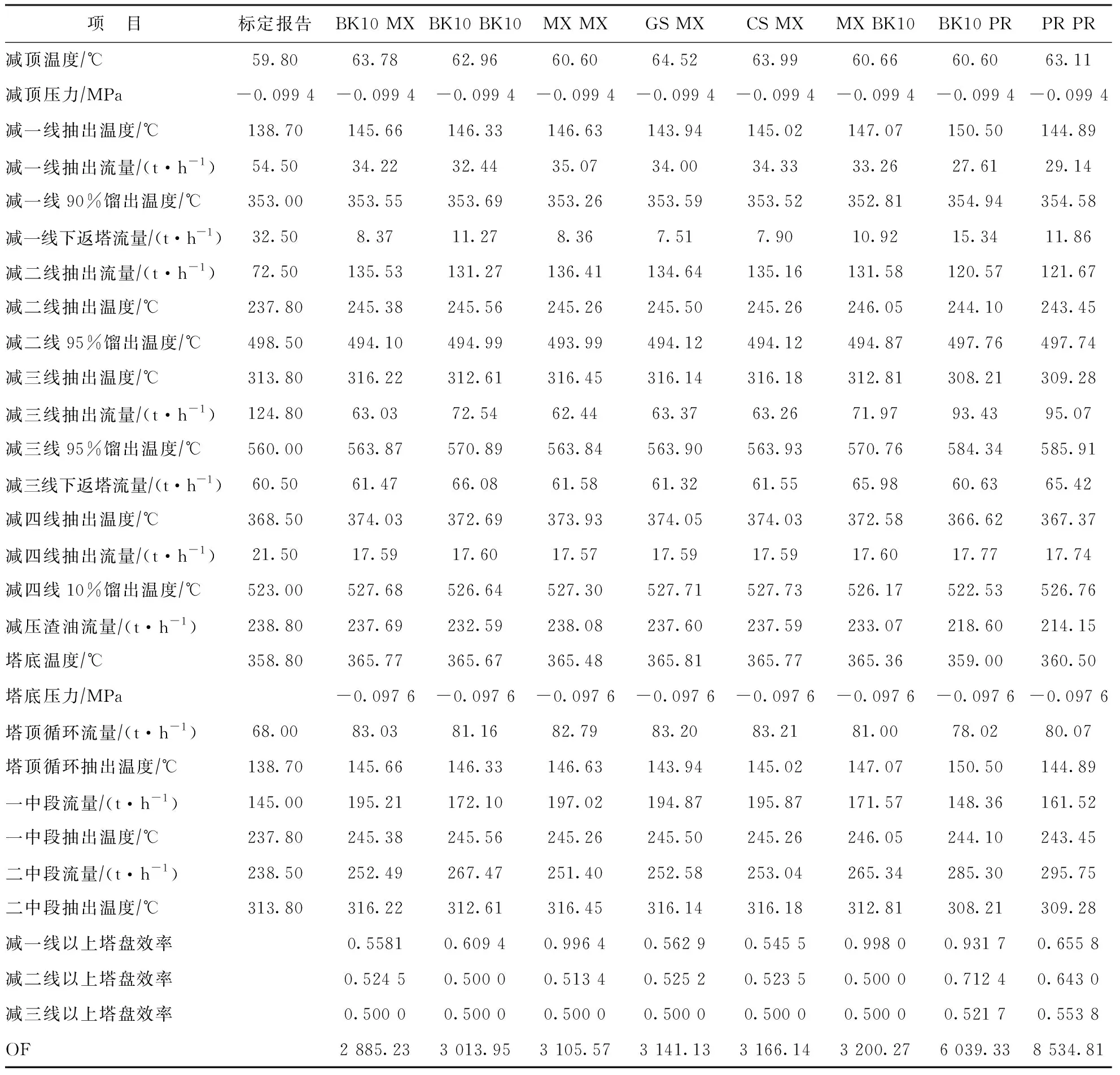
表4 不同物性计算方法对减压塔模拟结果的影响

4 不同方法影响模拟结果的理论解释

多元体系气液两相平衡要满足气相逸度等于液相逸度[12]。液相逸度有两种计算方法：一是活度系数法，Maxwell Bonnell、BK10、Grayson-Streed和Chao-Sea采用该方法；二是液相逸度用逸度系数计算，Peng-Robinson(PR)、Soave-Redlich-Kwong(SRK)和Redlich-Kwong-Soave(RKS)采用该方法。分离过程计算准确度主要受相平衡常数K是否准确的影响。RKS和SRK的PVT关系式是相同的，只是液体摩尔体积的计算方法有所不同。RKS采用API方法，SRK采用Peneloux体积校正因子。

GS和CS方法中气相逸度系数两者均采用RK状态方程，液相活度系数的计算都采用Scatchard-Hildebrand正规溶液模型。

在减压塔汽化段温度365 ℃、压力5 kPa的条件下，以减压渣油中平均沸点为579 ℃的虚拟组分为例，应用不同方法计算其K值，计算结果见表5。K值与液相活度系数、纯组分饱和蒸气压、纯组分饱和蒸气逸度系数、气相逸度系数有关。但从表5的计算结果可见，K值的大小主要与饱和蒸气压有关，且呈线性关系，相关系数达0.999 9，而其它系数几乎都等于1，影响很小。

从表5可见，RKS和SRK法计算的K值相同，但模型误差不同。这是因为塔的平衡方程中，除了相平衡方程外，还有能量平衡方程(焓平衡)，而液相焓计算需要用到液相摩尔体积，RKS和SRK的液相摩尔体积计算方法不同，从而导致最终计算结果不同。

表5 减压条件下不同物性计算方法所得相平衡常数

常压塔的计算类似，计算结果表明K值的大小主要与饱和蒸气压有关，但并不呈线性关系，常压下K值与液相活度系数、纯组分饱和蒸气压、纯组分饱和蒸气逸度系数、气相逸度系数均有关。

对比常压和减压下的K值，发现采用不同的物性计算方法对减压部分模拟时，K值相差较大，如PR法的K值是MX的2.74倍；不同的物性计算方法对常压部分影响不大，如PR法的K值是BK10法的1.06倍。这与多套装置的模拟经验完全相符。

(1)石油窄馏分的饱和蒸气压。应用API 5A1.19 Maxwell Bonnell关联公式计算579 ℃的虚拟组分在365 ℃下的饱和蒸气压，得0.327 kPa，又从文献[6]可知，该预测值比实际值高。

在Aspen Plus中MX方法计算的579 ℃虚拟组分在365 ℃下的饱和蒸气压是0.337 kPa，而实际值小于0.327 kPa。换言之，与实际值相比，用MX法预测时K值较大，常压渣油更易挥发，计算得到的减压渣油收率会偏低，这和实际经验吻合。从表5可见，K值按MX,BK10,CS,GS,RKS,SRK,PR依次增大，这和表1的减压部分模型按MX,BK10,CS,GS,RKS,SRK,PR的顺序，误差逐渐递增一致。

与实际值相比，在Aspen Plus中BK10法预测的饱和蒸气压数据比MX法偏差大。BK10法回归自大量相平衡测量数据，文献[9]指出BK10法所用原始数据中压力下限是68.95 kPa。由此可见，在减压塔和减压炉转油线的压力范围内，K值是外推的，因而误差比MX法大。但是在初馏塔和常压塔部分，由于BK10法直接根据实验值回归出K值，因此其误差最小。

CS，GS，RKS，SKR，PR方法采用不同的立方型状态方程模拟饱和蒸气压，但在低压和低温下，如平均沸点为579 ℃的虚拟组分在365 ℃下预测的饱和蒸气压数据偏差仍较大[13]。

综上所述，由于MX和BK10法是基于低压下实测数据回归的蒸气压方程或相平衡常数方程，因此这两个方法预测的饱和蒸气压最准确。CS，GS，RKS，SRK，PR法是基于立方形状态方程预测饱和蒸气压数据，而立方型方程本身就较难准确预测饱和蒸气压，因此误差较大。

(2)石油及常压渣油溶液的理想性。Hariu等[14]证明一般石油馏分在压力低于300 kPa条件下基本符合理想体系，石油馏分中某一窄馏分的相平衡常数可按Raoult定律求取。其液相活度系数、饱和蒸气逸度系数、气相逸度系数均可为1。表明对于处于低压的常压渣油溶液，气相和液相都可以近似作为理想体系和理想溶液处理。

CS和GS法把液相按正规溶液处理，计算出活度系数大于1，CS，GS，RKS，SRK，PR法用状态方程计算气相，计算出气相逸度系数小于1，这些都小幅增加了气液平衡常数。

由于GS法在CS法基础上对计算纯组分液相逸度系数的参数进行了更新，使GS法更适合在温度和压力提高后相平衡常数的预测。因此在减压部分，CS法误差小，而在常压部分，GS法误差小。

从表5可见，如果要更准确地模拟减压部分，需要进一步降低相平衡常数，液相的活度系数则应小于1，常压渣油可能是较弱的负偏差溶液。其原因可能是原油中的一些高分子极性化合物，如胶质、沥青质、稠环芳烃等，由于偶极相互作用、电荷转移π-π键作用和氢键作用，彼此发生缔合，形成“超分子结构”。这些超分子结构外表面的分子带有过剩的能量，形成一个附加的引力场，能够吸引一些分子量较小、芳香度较低的烃类。在原油蒸馏过程中，这部分烃类，由于受胶核附加引力的作用，在达到沸点时难以转入气相而滞留于重油中[15]。

5 结 论

(1)对于常减压蒸馏装置模拟，在Aspen Plus中推荐采用BK10法模拟常压部分、Maxwell-Bonnell法模拟减压部分，模拟结果与实际值最接近，且计算速率快。BK10法的计算误差是推荐方法的1.045倍。减压部分不能应用立方型状态方程预测气液平衡常数，误差大，计算速率慢。

(2)除正确选择物性计算方法外，常减压蒸馏装置的模型结构也很重要。减压部分模拟需要考虑减压炉转油线的两相分离以及减压塔汽化段的雾沫夹带，否则减四线的误差较大。

(3)从理论上解释了不同物性计算方法对常减压蒸馏装置模拟结果的影响。表明在减压环境下，常压渣油不是正规溶液，常压渣油可能是弱的负偏差溶液。

(4)应用EO建模法和理论分析，可以快速确定原油评价数据、各种工艺参数、化验分析数据的误差对模拟结果的影响，估算塔盘效率、塔盘压降、塔进料压力等不可测量或无测量的参数，以益于装置诊断、优化。

参考文献

[1] Remesat D.Improving crude vacuum unit performance[J].Petroleum Technology Quarterly，2008(3)：107-113

[2] Pilling M，Roza M，Wong S M.Entrainment issues in vacuum column flash zones[J].Digital Refining，2010(1)：1-10

[3] Golden S，Barletta T，White S.Vacuum unit performance[J].Digital Refining，2012(4)：1-6

[4] Golden S，Barletta T，White S.Myth of high cutpoint in dry vacuum units[J].Digital Refining 2014(2)：1-7

[5] 王健红，冯树波，杜增智，等.化工系统工程理论与实践[M].北京：化学工业出版社，2009：119-124

[6] Maxwell J B，Bonnell L S.Deviation and precision of a new pressure correlation for petroleum hydrocarbons[J].Ind Eng Chem，1957，49(7)：1187-1196

[7] Soave G.Equilibrium constants from a modified Redlich-Kwong equation of state[J].Chem Eng Sci，1972，27(6)：1197-1203

[8] Cajander B C，Hipkin H G，Lenoir J M.The prediction of equilibrium ratios—A nomogram of improved accuracy[J].J Chem Eng Data，1960，5(3)：251-259

[9] Chao K C，Seader J D.A general correlation of vapor-liquid equilibria in hydrocarbon mixtures[J].AIChE J，1961，7(4)：598-605

[10] Grayson H G，Streed C W.Vapor-liquid equilibria for high temperature，high pressure hydrogen-hydrocarbon systems[C]Sixth World Petroleum Conference.Paper No.20 PD7.Frankfurt，1963-06

[11] Peng D Y，Robinson D B.A new two-constant equation of state[J].Industrial and Engineering Chemistry Fundamental，1976，15(1)：59-64

[12] 郭天民.多元汽-液平衡和精馏[M].北京：化学工业出版社，1983：14-19

[13] 汪萍.立方型状态方程性能的评价研究[D].青岛：青岛科技大学，2004

[14] Hariu O H，Sage R C.Crude split figured by computer[J].Hydrocarbon Processing，1969，48(4)：143

[15] 梁文杰.石油化学[M].东营：石油大学出版社，1995：64-65