视频分析软件Tracker在复摆实验中的应用

曾 蓓,程敏熙

(华南师范大学 物理与电信工程学院，广东 广州 510006)

复摆实验是大学物理实验中的重要实验. 本文对复摆实验进行了改进，通过对复摆摆动过程进行拍摄，并利用Tracker软件跟踪轨迹，拟合后通过计算得到复摆振动周期，进而绘制关系曲线图像，并用2种数据处理方法计算重力加速度，从而简化了3实验.

1 复摆的运动原理

在忽略空气阻力影响的情况下，质量为m的复摆在重力矩作用下运动，周期为

(1)

其中I为复摆通过悬挂点的转动惯量，h为质心到悬挂点的距离. 根据刚体转动惯量的平行轴定理有I=I0+mh2，其中I0为复摆绕通过重心且沿水平方向的轴的转动惯量. 代入式(1)中，得

(2)

(3)

与单摆的周期表达式相比，此时的等效摆长为

(4)

通常情况下，与复摆的某个振动周期T对应的h值分别为h1和h2，2个值对应的等效摆长相等，代入式(4)并整理得a2=h1h2，再代入式(4)后，得l=h1+h2. 通过实验所得数据绘制出的T-h关系曲线，可得与任一振动周期T相对应的等效摆长，故振动周期T可表示为

(5)

2 测量重力加速度的方法

根据复摆的运动规律，有2种计算重力加速度的方法：

1)等效摆长法. 根据式(5)，取T-h关系曲线(如图1所示)中同一振动周期对应的2个值h1和h2，求得出等效摆长后，代入式(5)中求得重力加速度g.

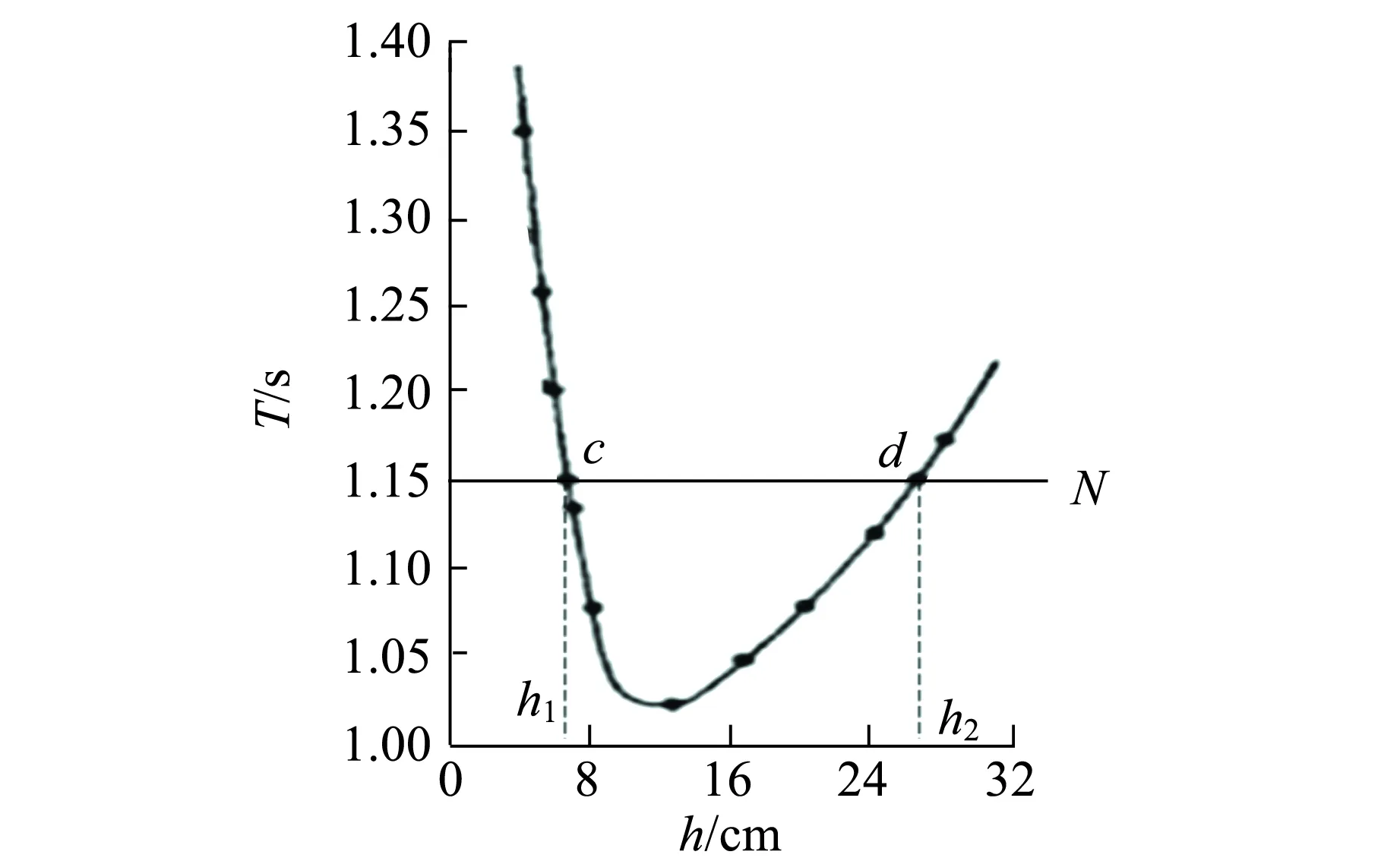
图1 等效摆长示意图

2)直线拟合法[1]. 由式(2)变形可得

(6)

做T2h-h2的关系直线图，求直线斜率进而求g.

3 实验步骤及数据分析

1)实验仪器

复摆由钢尺每隔3 cm钻孔制成，因是自制的实验仪器故其质心位置未知，可采用悬挂法测出复摆的质心.

2)运动过程拍摄

依小孔顺序将复摆悬挂在铁架台上，在复摆下部贴一白色小纸片作为跟踪标记，拍下复摆在平面内小角度摆动过程，直至将所有不同小孔悬挂时的摆动过程拍摄完毕.

3)选定并追踪复摆的振动轨迹

进入Tracker的主界面打开拍摄的视频后，选取合适的片段进行追踪，创建1个质点后，长按“Ctrl+Shift”键，同时用鼠标左键点击纸片，并选择需要追踪的纸片的模板，选择自动追踪并按下搜索键，得到复摆运动的轨迹点，如图2所示.

图2 Tracker主界面及质点追踪过程

4)数据处理

将鼠标移至右上方的位移-时间关系曲线，点击“分析”按钮，即可弹出数据处理的窗口，点击“拟合”，便会根据物体运动过程的图像描绘出拟合曲线，并在下方给出拟合曲线方程的相关数据. 为使图像的拟合更加准确，根据阻尼振动公式，可将公式编辑为[2]

x=A*exp (-B*t)*sin (C*t+D)，

并根据拟合方程的数值得到复摆的振动周期，如图3所示.

图3 位移-时间拟合图像

按照上述方法可求出复摆的第1个孔悬挂于铁架台时的振动周期为T=1.268 s，同理根据此方法可依次求得复摆上的其他小孔悬挂于铁架台时的振动周期. 将复摆每个悬挂点对应的周期及质点到悬挂点间的距离的数据整理到表1中.

表1 复摆实验的相关数据

5)计算重力加速度

a.等效摆长法

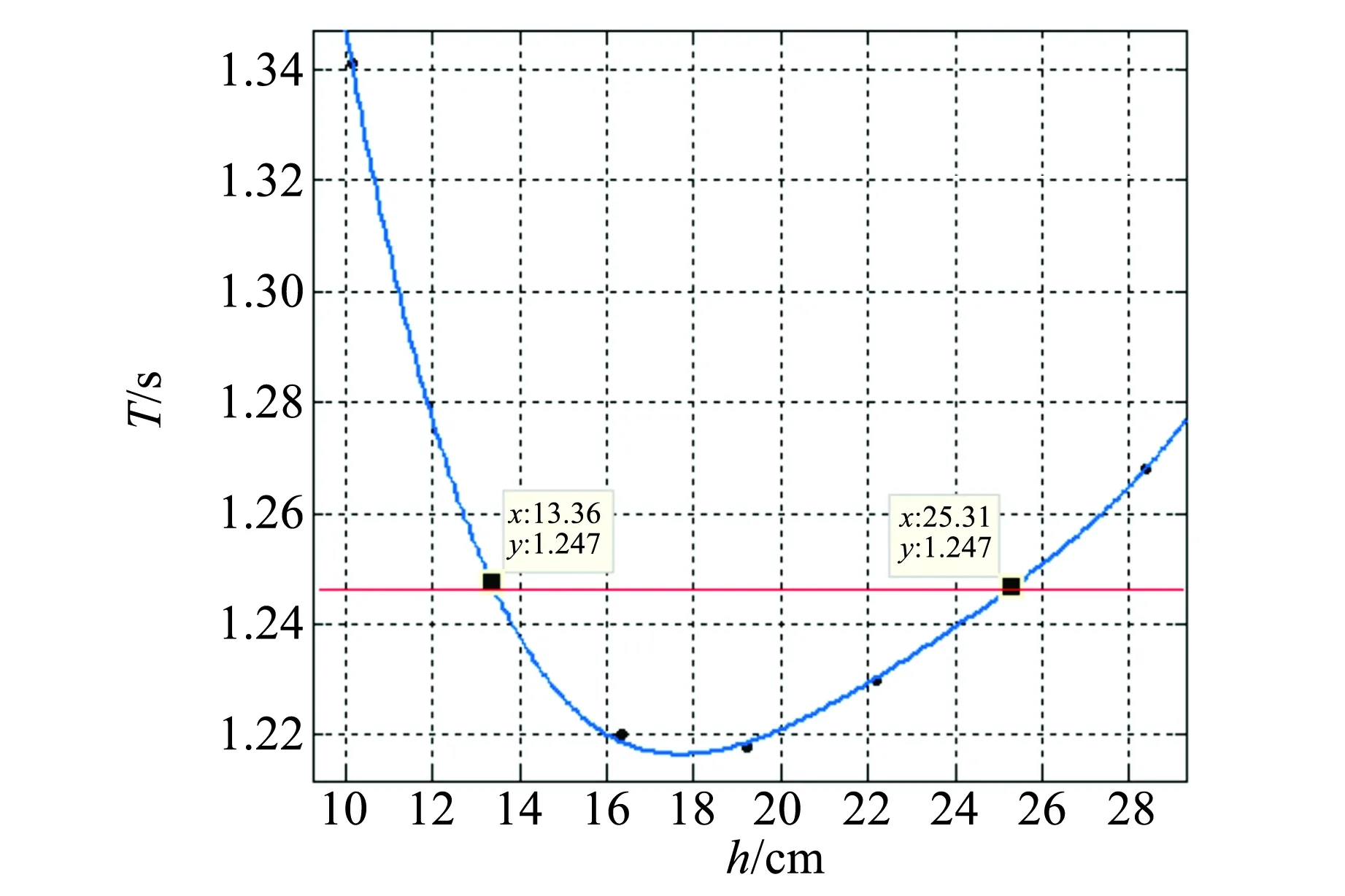
图4 等效摆长取值示意图

取用Matlab软件所绘制出的T-h关系曲线中同一振动周期的对应的2个h值，如图4所示. 从图4可以看出， 当悬挂点逐渐远离复摆质心的过程中，其振动周期先逐渐变小，达到最小值后，又逐渐增大. 图4中根据所测得的实验数据绘制出的T-h图像与文献[3]中的相一致.

T=1.247 s时对应的h值分别为13.36 cm和25.31 cm，得出等效摆长L=38.67 cm，求得重力加速度为g=9.817 m/s2. 由于该实验是在广州地区进行，通过查阅资料可知，广州地区的重力加速度值为g=9.788 m/s2. 计算得到实验值与公认值的相对偏差为0.3%.

b.直线拟合法

根据式(6)，选取中间部分数据点，作出T2h-h2的关系图像并进行拟合，其中T2h和h2的数据如表2所示. 根据表2画出T2h-h2关系图，如图5所示. 经拟合得：斜率k=4.017，截距b=0.137 1，相关系数R2=0.999 8，故g=9.827 m/s2,相对偏差为0.4%.

表2 T2h和h2的相关数据

图5 T2h-h2关系图

4 结束语

用复摆法测量重力加速度的实验中，关键在于测量复摆的振动周期. 通过上述实验可以看到，用拍摄实验视频的方法，辅以Tracker软件的轨迹追踪和数据分析，使本实验相对于传统的复摆实验来说，简化了实验仪器的同时，还使得操作简洁高效. 实验者可以利用身边有摄像功能的手机或相机进行拍摄，并用电脑软件进行分析，有利于提高实验者的兴趣.

参考文献：

[1] 陈思佳,张文霞,杨启凤,等. 线性回归法和Matlab在复摆测重力加速度实验中的应用[J]. 物理实验,2009,29(3):44-46.

[2] 王经淘,程敏熙,贾昱,等. 利用Tracker软件分析气垫导轨上弹簧振子的阻尼振动[J]. 大学物理,2014,33(4):22-24.

[3] 熊永红,张昆实,任忠明,等. 大学物理实验(第一册)[M]. 北京:科学出版社,2007:87-89.

[4] 李静,厉志明. 普通物理实验[M]. 广州：华南理工大学出版社,1994:82-85.

[5] 闫凤武. 对复摆实验的一点改进[J]. 河北民族师范学院学报,2014,34(2):40-41.

[6] 赖才,程敏熙,黄慧敏. 用视频分析软件Tracker研究单摆的运动[J]. 物理教师,2016,37(12):67-69.

[7] 陈明伟. Tracker视频分析软件在“研究抛体运动规律”实验中的应用[J].物理通报,2017(5):102-104.