磁光捕获冷原子和玻色-爱因斯坦凝聚的研究进展

宋晓丽,冯 放

(1.Institut Non linéaire de Nice, Alpes-Maritimes Valbonne 06560;2.Department of Physics and Astronomy, Northwestern University,Illinois Evanston 60208;3.东北农业大学 理学院，黑龙江 哈尔滨 150040)

1 磁光捕获冷原子和玻色-爱因斯坦凝聚研究的发展历史

1901年和1933年Lebedev及Nichols和Hull分别证明了光的辐射压力可以作用于原子. 随着激光的发展，1975年提出了多普勒激光冷却原子方法，1987年Raab等人发展了第一个磁光阱(magneto-opticaltrap,MOT)，这是冷原子发展史上重要的一步.

在足够低的温度时，原子将会处于新的量子物态. 对于玻色型原子气会产生玻色-爱因斯坦凝聚；对于费米型原子气，则形成简并费米气.

玻色-爱因斯坦凝聚(Bose-Einsteincondens,BEC)几乎已经发展了100年. 1920年代，玻色-爱因斯坦凝聚的理论被提出来. 1924年印度物理学家玻色提出了以不可分辨的n个全同粒子的新观念，使得每个光子的能量满足爱因斯坦的光量子假设，也满足玻尔兹曼的最大概率分布统计假设，光子理想气体的观点可以说是彻底解决了普朗克黑体辐射的半经验公式的问题. 可能是当初玻色的论文因没有新结果，遭到了退稿. 他随后将论文寄给爱因斯坦，爱因斯坦意识到玻色工作的重要性，立即着手研究这一问题，并于1924年和1925年发表2篇文章，将玻色对光子(粒子数不守恒)的统计方法推广到原子(粒子数守恒)[1-2]，预言当这类原子的温度足够低时，会有相变——新的物质状态产生，所有的原子会突然聚集在尽可能低的能量状态，这就是玻色-爱因斯坦凝聚(BEC)[3]. 1995年首次在实验室实现玻色-爱因斯坦凝聚，其温度大约是几百nK. 玻色-爱因斯坦凝聚具有超流性、超导性、波动性、干涉性和衍射性，可以说玻色-爱因斯坦凝聚中的玻色子呈现了光子的特性. 有人甚至探索把玻色-爱因斯坦凝聚通过波导，如同光通过玻璃一样.

2 磁光捕获冷原子

磁光捕获的原子是维持在μK的原子. 漫射气体与激光场的相互作用，能磁光捕获原子团.

2.1 MOT-磁光阱

关于磁光捕获(magneto-optical trap，MOT)的具体理论可以参考文献[4]. 图1为磁光捕获的磁场光场图[5]. 用亥姆霍兹线圈产生磁场，磁感应强度的变化如图2所示，中心点磁感应强度为0. 光场分别为失谐量为δ≃-Г/2 (红失谐光)的左旋光和右旋光，Г为原子跃迁线宽，而原子上能级的衰退(自发辐射)常量为τ=1/Г. MOT需要运用光场和磁场共同作用来捕获冷原子.

图3为磁光捕获的能级图[4]. 右旋光作用在m=0到m=1的2个能级上；左旋光作用在m=0到m=-1的2个能级上.

图1 磁光捕获的磁场光场图

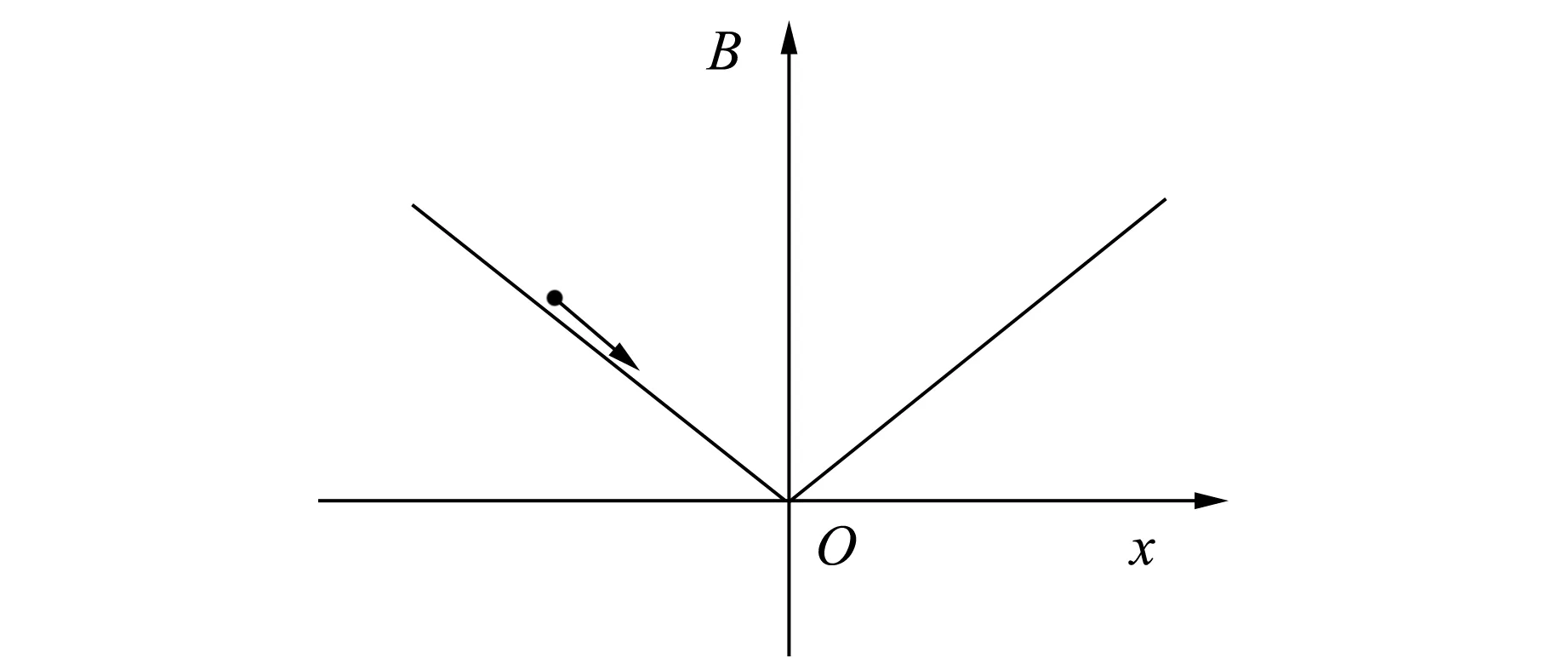
图2 磁感应强度的变化

图3 磁光捕获能级图

2.2 磁阱

对于磁场，需考虑塞曼效应，磁场越强，原子的能级分裂就越大. 如图2所示，2个对着的亥姆霍兹线圈产生磁感应强度中间为0，越向两边，磁场越大. 而对应的原子能级分裂，如图3所示，在磁场中心，能级之间没有分裂. 随着磁场的增强，m=-1,m=0,m=1，分裂越大. 对于中性原子，磁场捕获公式为

U(r)=-μ·B(r)，

其中μ为磁偶极矩，U为磁场势能，B为磁感应强度. 由于磁场的线性变换，从而导致了塞曼效应

U(r)=gFmFμB|B(r)|,

μB为玻尔磁子(μB/h≈1.4 MHz/G),gF为超精细结构的朗德g因子，mF是电子总角动量F在z方向投影的量子数.gFmF>0时，原子才会被捕获. 因此可以用非均匀的磁场制造出磁阱来捕获原子. 由麦克斯韦方程，在静磁场中只允许有区域极小值，所以只有在(low field seeker)下的原子才能被捕获.87Rb在低磁场的状态下有|F=2,mF=2〉(gF≃+1/2),|F=2,mF=1〉(gF≃+1/2)以及|F=1,mF=-1〉(gF≃-1/2)的状态是趋向磁场较小状态. 但由于碰撞特性使得|F=2,mF=1〉在磁阱中的生命期很短,所以最后能被磁阱捕获的只有|F=2,mF=2〉,|F=1,mF=-1〉.

2.3 光阱

光的作用力有光的辐射压力和偶极力.

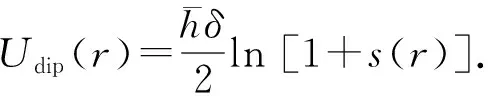
2.4 多普勒冷却

多普勒冷却法基于失谐和多普勒效应实现. 假设1个原子的速度为v,会导致频移Δω=-k·v,如图4所示，对于速度为v的原子，光束1看到的频率为ω1，而光束2看到的频率为ω2.

图4 多普勒冷却原理图

如果光是红失谐光，而且没有饱和跃迁，因为多普勒效应，原子会移向散射更多光子的源，而不是远离这个源. 通过用2个相对的红失谐激光，光所施加的力依赖于速度，如图5所示，α为摩擦系数，k为劲度系数，类似摩擦(F=-αv)，所以这样也减慢了原子速度，从而达到制冷.

图5 光施加力与速度的关系

3 玻色-爱因斯坦凝聚

3.1 玻色-爱因斯坦凝聚

玻色-爱因斯坦凝聚表示原来不同状态的原子突然“凝聚”到同一状态(一般是基态)，即处于不同状态的原子“凝聚”到了同一种状态，所有的粒子都一个行为，其行为就好像1个玻色子的放大. 爱因斯坦曾经预言：当原子团的相空间密度超过 2.612时，高能级的原子数目会受到限制，而最低能级上的原子数则不受这一条件约束，因此大量的原子会凝聚在最低能态上，这种现象被称为玻色-爱因斯坦凝聚. 图6为玻色-爱因斯坦凝聚的密度分布图[7]，由图可知，温度越低，玻色-爱因斯坦凝聚越纯，密度越集中.

图6 玻色-爱因斯坦凝聚的密度分布

一般的原子都是随机移动的，假设原子之间的平均距离为d，温度比较高，原子之间的距离比较远；当原子温度很低时，原子之间的距离就会很近，而到达德布罗意波长d=λdB时，即为玻色-爱因斯坦凝聚. 德布罗意波长λdB为

3.2 磁光捕获与玻色-爱因斯坦凝聚的不同

图7充分显示出磁光捕获和玻色-爱因斯坦凝聚的不同. 磁光捕获温度比较高，温度为μK左右，原子密度分布为高斯分布，摄得图像为比较圆的原子团. 而玻色-爱因斯坦凝聚温度为nK量级，密度非常集中地分部在中心，密度曲线已经不满足高斯分布，而且由于重力作用，去除捕获场，在自由落体的一定时间内，玻色-爱因斯坦凝聚显示的为椭圆型.

(a) 磁光捕获 (b) 玻色-爱因斯坦凝聚 (T=600 nK) (T=300 nK)图7 磁光捕获与玻色-爱因斯坦凝聚原子密度分布

图8(a)为磁光捕获，原子温度高，密度小，d≫λdB,原子分布也在不同的能级上. 而图8(b)为玻色-爱因斯坦凝聚，原子温度低，密度很大，d≤λdB,原子很集中的大部分都分布在基态.

图8 磁光捕获与玻色-爱因斯坦凝聚的比较

3.3 玻色-爱因斯坦凝聚的物理特性

1)物质波的相干源(可以做为原子激光)

玻色-爱因斯坦凝聚已经呈现光子特性，每个玻色子都可以看成光子，在2006年Guerin等人实现了玻色-爱因斯坦凝聚通过光波导的实验研究. 如果用Rb实现玻色-爱因斯坦凝聚，那么Rb玻色-爱因斯坦凝聚就可以通过光波导传播，如同光子通过玻璃一样(如图9所示)[8].

图9 玻色-爱因斯坦凝聚通过光波导实验

2)超流性和超导性

图10 玻色-爱因斯坦凝聚超流现象的实验结果

在理论中，玻色-爱因斯坦凝聚的超流体中的无摩擦现象于1962年被提出，1972年提出了超导中的库泊电子对无电阻现象，即玻色-爱因斯坦凝聚没有电阻，流体没有摩擦. 图10是2000年Madison等人实现的玻色-爱因斯坦凝聚超流现象的实验结果[9].

3)干涉性和衍涉性

玻色-爱因斯坦凝聚已经可以看成物质波，2个玻色-爱因斯坦凝聚可以互相干涉，并且产生干涉条纹，如图11所示[10].

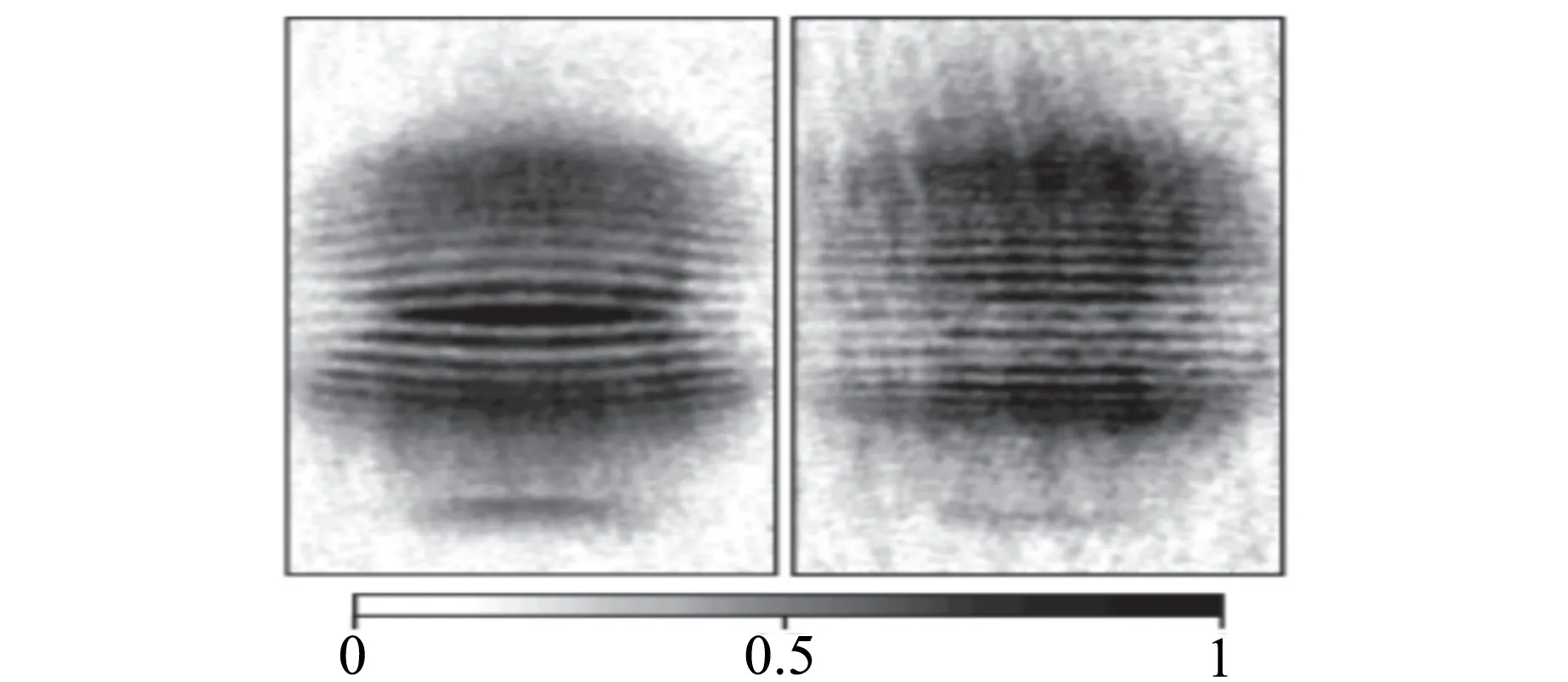
图11 2个玻色-爱因斯坦凝聚产生的干涉条纹

4)可调谐的相互作用(费什巴赫共振)

由于超冷原子系统可以直接构造哈密顿量，体系干净，参量可调，所以越来越多的理论模型在这个平台上实现. 而费什巴赫共振就是超冷原子实验中的一个实验手段.

5)BEC +光电势=“量子模拟”，模仿绝对控制的固态物理模型

利用光与原子间的偶极力形成的光晶格可以将冷原子束缚住并有序排列，如图12所示[11]，Greiner在2003年的实验研究，通过调节势阱深度可以很好地调节原子间的耦合强度，从而可以直接构造体系的哈密顿量，实现量子模拟[12].

6)莫特绝缘体

莫特绝缘体是一类在常规能带理论下应导电的材料，但在测量时(特别是在低温下)是绝缘体. 这种效应是由于电子-电子相互作用造成的，这在传统的频带理论中没有考虑到，如图12所示[11].

图12 冷原子的束缚和有序排列

3.4 压缩磁光阱

要得到BEC，不得不提到压缩磁光阱(Compressed magneto-optical trap,CMOT)过程，原子团被压缩，也称为temporal dark MOT. 在磁场光场开启，加载MOT到稳定状态后，需要开启CMOT过程，在这个过程中，光的失谐从δ=-3.5Г变为δ=-8Г. 磁场从加载磁场为2×10-5T/cm 变为B2′=6.55×10-3T/cm. 失谐的改变，降低了多重散射导致的原子之间的排斥，当磁场梯度增加，导致捕获劲度系数增加的变化. 从而导致原子团收缩，密度和碰撞率都增加了3个数量级. 这个过程也使得MOT更好，形状和对称性都更好. 通过补偿磁场的作用，CMOT的位置可以精确地调整到最适合磁场捕获的位置.

3.5 Molasses过程

要得到BEC, Molasses过程也不可少，比如开水，会散发水蒸气，这样就能保持开水的温度在100 ℃. 比如1个Rb原子团，撤去磁场，让Rb原子团散发，由于这种散发会迅速吸收原子团的温度，从而使得Rb原子团内部的温度骤降[13]. Molasses过程会使得原子团在3 ms的光学Molasses时间内迅速制冷到80 μK，在此期间，磁场被关闭，光场改变为δ=-10Г. 虽然这个温度还远高于西西弗斯极限，原子团还会在后面进一步的冷却.

3.6 蒸发冷却

从冷原子到玻色-爱因斯坦凝聚，至关重要的一步是蒸发冷却. 蒸发冷却是达到nK 温度的最后步骤. 在低温下，原子之间会互相排斥，虽然可以将原子团的温度降到μK量级，却很难达到很高的密度. 为此要剔除一部分原子来提高原子的相空间密度， 进一步降低原子团的温度，即蒸发冷却，把温度高的原子滤出去. 可采用的方法有射频波，还有加入外加磁场，控制磁场深度，从而失去较高能量的粒子，达到冷却的目的.

1)射频波

如图13所示,当射频场开启时，满足小失谐条件的地方处于低场趋近态的原子会被抽运到其他状态. 如果被抽运到mF=0这个磁场态，原子就会自由飞出磁阱捕获；如果被抽运到高场趋近态上，原子就会被排斥出磁阱. 所以当射频频率从高频开始向低频扫描时，能量高的原子接近小失谐区域的概率更大，这样它们更容易被滤除出磁阱，从而达到蒸发冷却的效果.

图13 低场趋近态原子抽运

2)外加磁场法

芝加哥大学的Cheng Chin小组，用外加磁场法使磁场势阱变浅，滤除高势能态的温度较高的冷原子，从而达到蒸发冷却的目的，得到玻色-爱因斯坦凝聚，如图14所示[14].

图14 外加磁场法蒸发冷却得到玻色-爱因斯坦凝聚

图15是经过RF蒸发冷却后得到BEC的示意图，实验中，在10 s内改变RF的频率范围为20～1.3 MHz，然后维持在1.3 MHz. 图16为对应的原子团截面的高斯耦合图，以对应的原子团的温度和数量. 由此可见，RF能很好地蒸发冷却，从而得到玻色-爱因斯坦凝聚.

图15 经RF蒸发冷却后得到BEC

图16 原子团截面的高斯耦合图

4 3种得到玻色-爱因斯坦凝聚的方式

1)用双腔结构实现制备大玻色-爱因斯坦凝聚团，其中一个腔制备大量的冷原子，另一个腔制备玻色-爱因斯坦凝聚.

2)用一个腔来同时实现冷原子的制备和玻色-爱因斯坦凝聚的制备. 如芝加哥cheng chin小组就是在一个腔内实现冷原子制备，再得到BEC的过程[14]. 这种方法的缺陷是难以得到大玻色-爱因斯坦凝聚团.

3)用atom chip得到BEC，他们用chip上的各种线路，以及非常小的外加磁场来获得BEC，优点是chip空间非常小，能在非常小的空间上制备出BEC[15-17].

5 磁光捕获和玻色-爱因斯坦凝聚实验基础

5.1 铷原子的能级结构和激光波长选择

实验中，用87Rb得到磁光捕获和玻色-爱因斯坦凝聚[6]，采用的原子能级如图17所示. 半导体激光器1发出的波长，经过声光调制器(AOM)移频，作用到磁光捕获，波长变为冷原子制冷光. 推送光是从第1个磁光捕获腔推送磁光捕获的冷原子团到第2个捕获腔的推送激光. 塞曼抽运光可以极大地提高磁场捕获的原子数量，如图18所示[6]. 而吸收图光为冷原子吸收的探测光. 半导体激光器2主要是用来做再抽运，把F=1的粒子都泵浦到F=2上，这样MOT才能捕获F=2的冷原子. 所以无论是入射到MOTs的冷原子制冷光,还是推送光，塞曼光都需加入再抽运光.

图19为光路的设置和AOM对应的频移，把最后的激光入射到MOT1和MOT2[6]. 实验用了2个腔，第1个腔捕获大量的冷原子，然后用推送光把第1个腔中的冷原子推到第2个腔. 第2个腔的空间小，这样磁场作用就强，磁阱深度就会够深，能极大地压缩冷原子，从而容易得到BEC.

图17 87Rb原子能级图

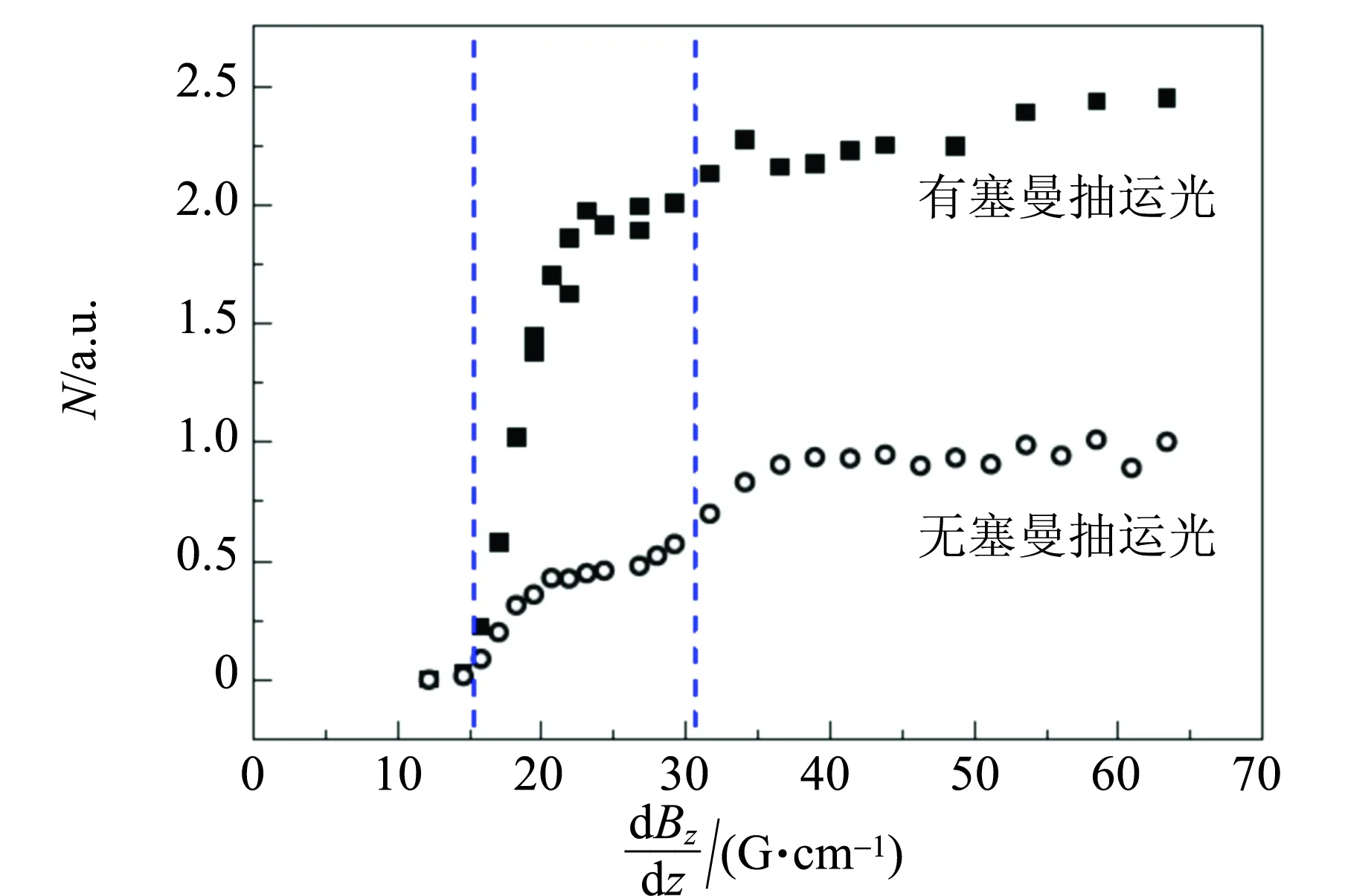
图18 磁场捕获原子

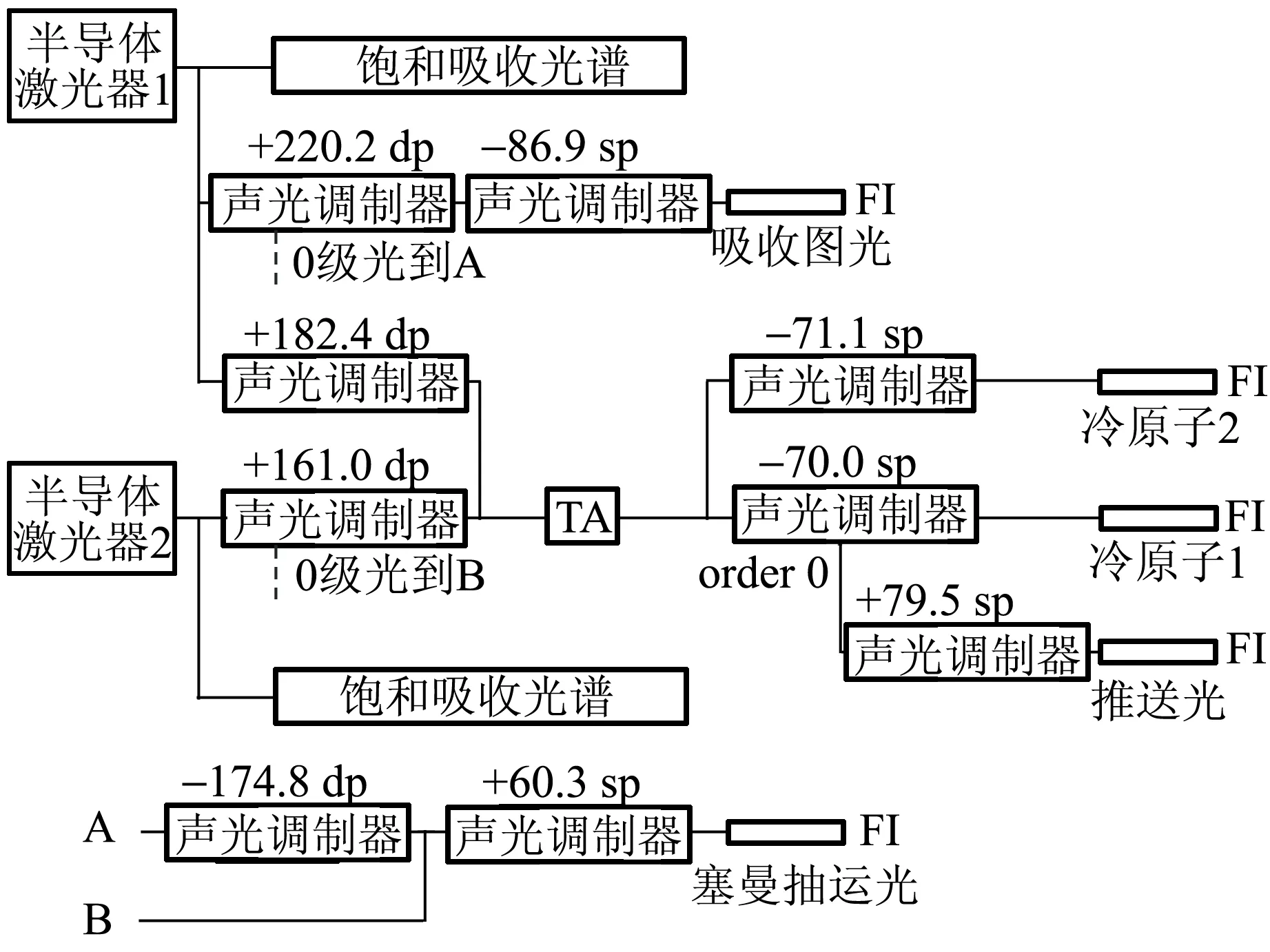
图19 设置光路和AOM频移

5.2 锁频的实现

为了得到冷原子，需要稳定的激光波长，所以需要锁频. 将MOTs光锁频到F=2→F′=3的频率上，如图20(a)所示的(2,3)峰值上. 而再抽运光锁频F=1→F′=2的频率上，如图20(b)所示的(1,2)峰值上[6].

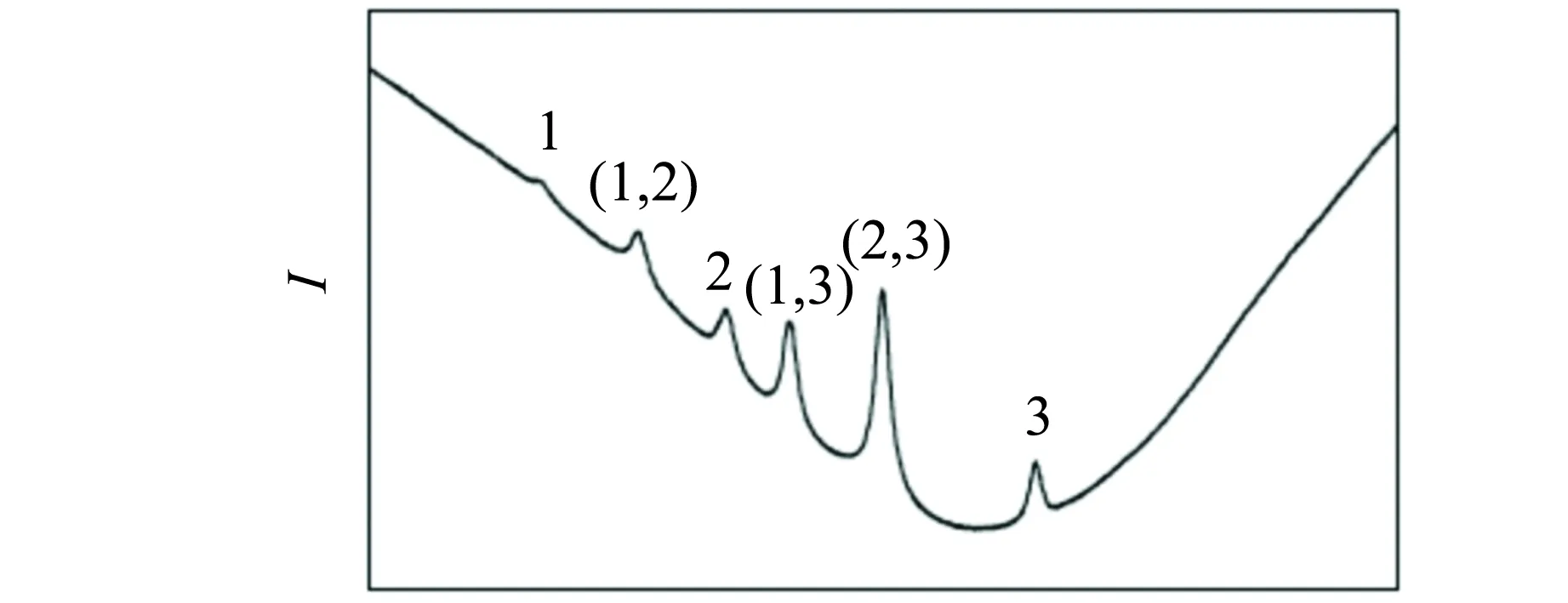
(a)F=2 to F′

(b)F=1 to F′图20 Rb的吸收光谱

搭建图21所示的锁频光路来获得铷原子的吸收光谱. 探测器探得的Rb的吸收光谱如图20所示. 运用电子电路使得激光锁定稳定在各个峰值点上. 图21中v为原子速度. 因为δ的存在，使得不同能级跃迁的吸收光谱峰值错开，从而能容易地锁频. 图21中强光和弱光须在一条直线上，这样才能更好地同时作用于更多的原子，得到清晰的吸收峰值.

图21 锁频光路

5.3 探测

探测冷原子及测量冷原子的温度、数量等参量需要探测系统. 图22所示为冷原子的荧光探测和吸收探测. 捕获了冷原子后，关闭所有的激光、入射探测光(图17的吸收图光)，冷原子就会吸收探测光，从而在吸收图像的摄像头上留下吸收图像，调节探测光亮度，使得摄像头不曝光，从而得到吸收图，测出冷原子或者玻色-爱因斯坦凝聚的温度、直径、数量等. 而荧光摄像头是为了能看到冷原子. 如图23中，红色的原子团能用摄像头清楚地看到.

图22 冷原子的荧光探测和吸收探测

5.4 实验搭建

图23为实验室里搭建光路. 整个系统分为2个腔，MOT1和MOT2. MOT1的真空度不高，大约为10-7Pa，这里大约能加载1010～1011原子数量. 推送光从上往下推，把第1个腔中的冷原子推到第2个腔中，第2个腔中，真空度比较高(<10-9Pa). 在第2个腔中，大约能得到109～1010原子数量. 图24是对应的MOT1和MOT2里原子的荧光图. 从图24中，可清楚地看见推送的光把MOT1里的原子推到MOT2里. 激光的参量为：b′=1×103T/cm；I为每光束几 mW.

图23 用摄像头拍摄红色原子团

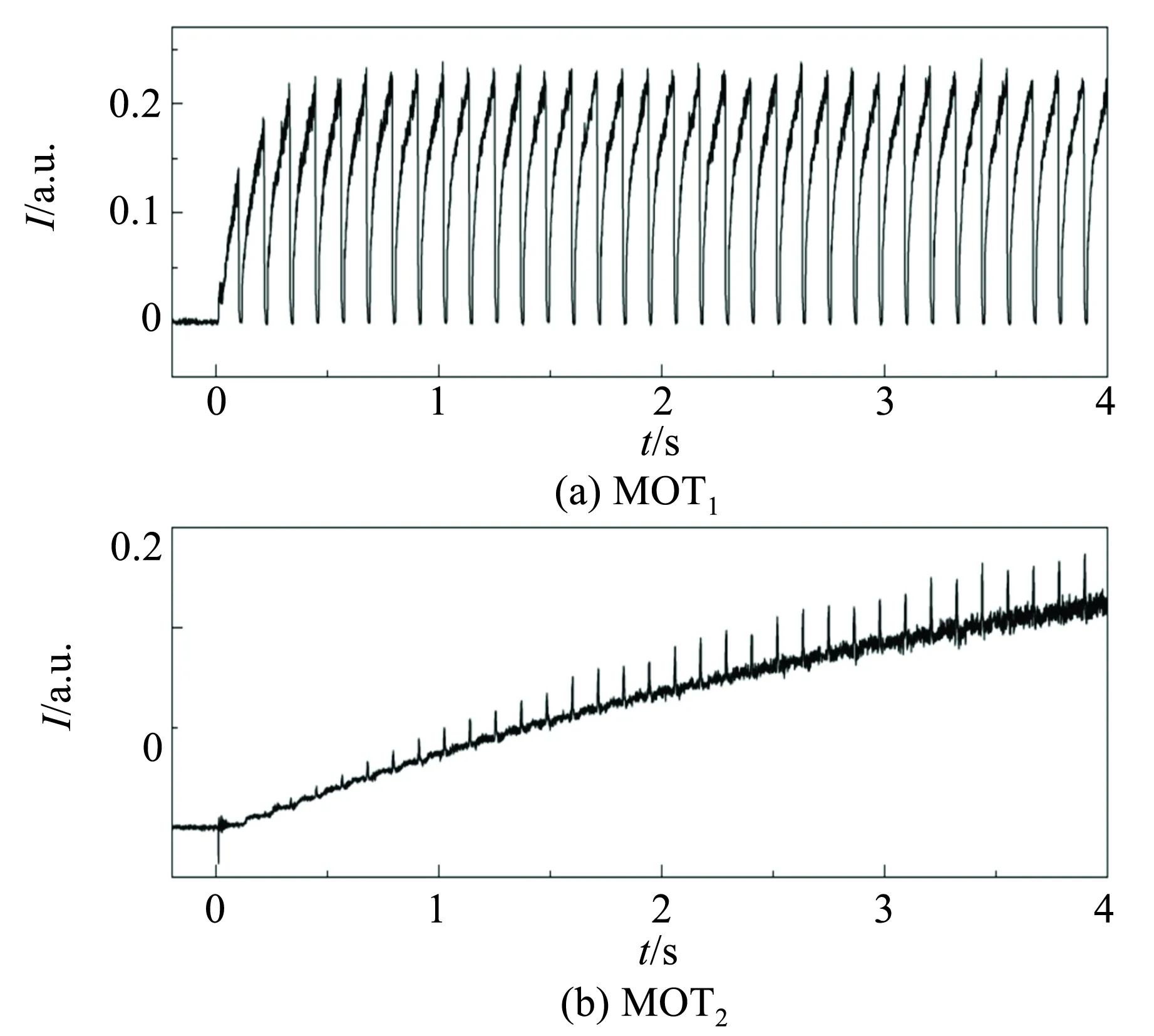
图24 MOT1和MOT2中的原子荧光团

用6个光纤把激光入射到MOT1里，再用另外6个光纤把激光入射到MOT2里. 耦合的光路图，如图25所示. 调节偏振片的方向，使得6束光的强度一样，并且3个为左旋光，3个为右旋光.

图25 耦合光路图

5.5 实验磁场及器材

实验用QUIC磁场捕获来得到玻色-爱因斯坦凝聚[18]. 因为在磁场中，中心点的磁感应强度为0，所以玻色-爱因斯坦凝聚会从这里漏出去，所以必须修堵该漏点. 一种方法是用QUIC磁场技术，使得磁场移动，然后磁场的0点处提升，从而达到堵住磁场0点的目的. 如图26所示，磁场右移约8 mm，而磁场0点提升. 我们采用的如图27所示的磁场阵列.

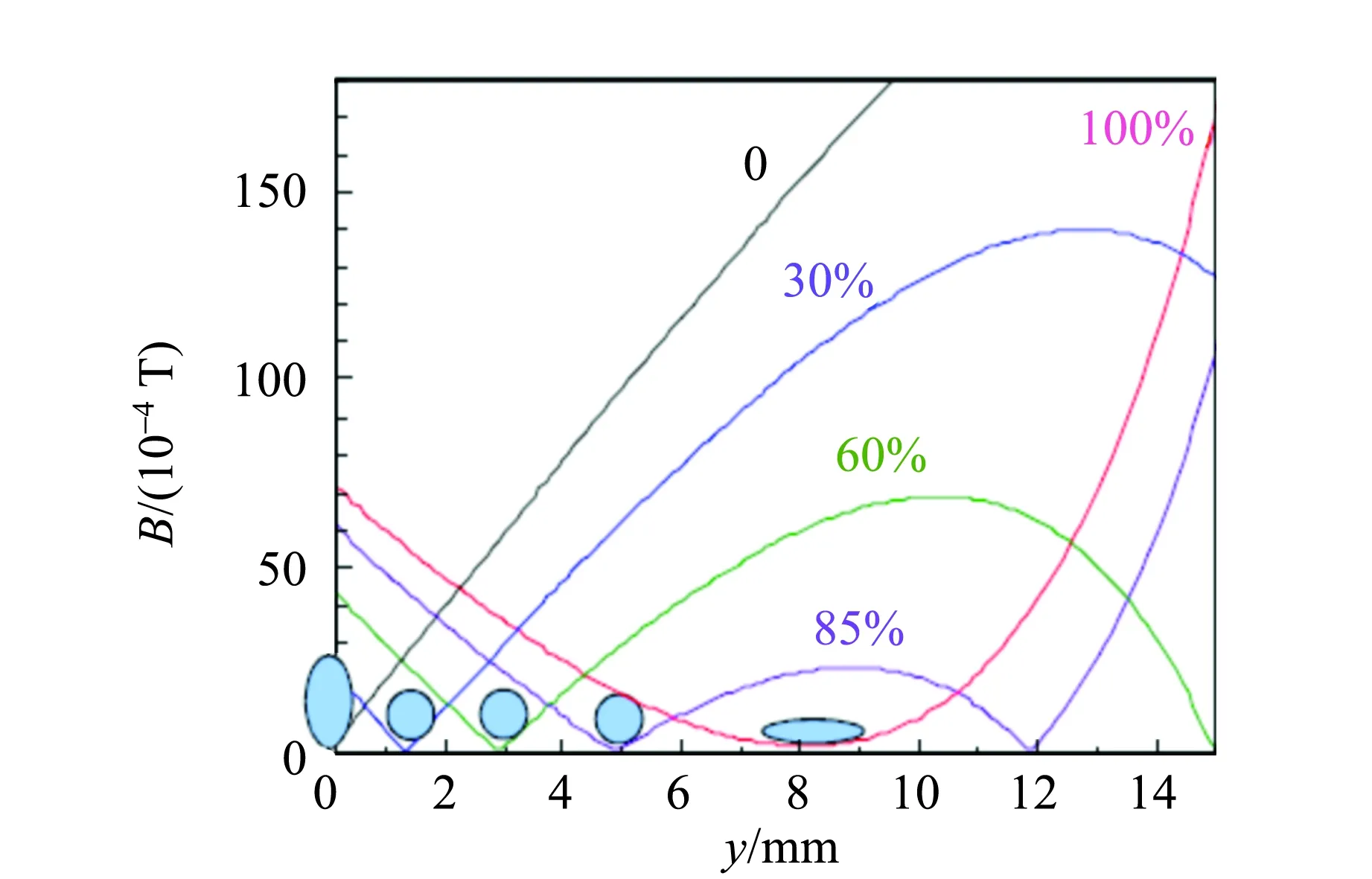
图26 磁场移动堵漏

图27 磁场阵列

图28(a)就是QUIC捕获磁场图以及电路系统图. 图28(b)中其他6个小线圈为磁场弥补场，来抵御外界干扰磁场.

(a)

(b)图28 QUIC捕获磁场图

还有一种方法可以堵住磁场0点，就是加插入光，用光场堵住磁场0点. 光场偶极力势能为Udip∝I/δ，从而红失谐和蓝失谐对原子的力就不同.δ>0为红失谐光，δ<0为蓝失谐光，如图29所示. 所以可用蓝失谐光堵住磁场0点.

图29 红失谐光与蓝失谐光的区别

2005年D. S. Naik和C. Raman等人用用聚焦的蓝失谐光与磁场0点重合. 从而堵住磁场0点，得到玻色-爱因斯坦凝聚. 如果光是圆形的，则得到环状的玻色-爱因斯坦凝聚. 如果光是扁的，则得到2个分离的玻色-爱因斯坦凝聚(如图30所示)[19].

图30 用聚焦蓝失谐光得到玻色-爱因斯坦凝聚

实验设备：实验需要2个激光器(1个为捕获MOT的激光器，1个为再抽运激光器). 2个激光器的功率放大器(因为需要捕获很多原子，而且把这些原子压缩捕获，所以需要大功率的激光)，激光锁频电子设备，若干AOM(用实现移频)，磁场，RF产生仪器，光纤，各自棱镜，透镜，镜片，波片，离子泵2个(1个抽真空度一般，1个要抽真空度非常好)，Ti泵(为了去除腔内的杂质)，几个摄像头，磁场探测器等. 可参考文献[6]所列的仪器设备.

6 磁光捕获和玻色-爱因斯坦凝聚的参量实验测量

图31为实验室得到的磁光捕获和玻色-爱因斯坦凝聚的对比图. 图31(a)图为磁光捕获，冷原子被捕获后，撤掉捕获场，让磁光捕获冷原子自由落体，自由扩散，随着时间增加，可以看出磁光捕获冷原子是扩散的. 而图31(b)为BEC，撤掉捕获场后，BEC由于重心作用，从横向椭圆形变成纵向椭圆形，基本上没有扩散.

(a)磁光捕获(T=1 μK)

(b)BEC(T=300 nK,N=2×105)图31 磁光捕获和玻色-爱因斯坦凝聚对比图

6.1 温度测量

采用如图32所示的吸收图测量冷原子温度. 根据飞行时间τTOF测出冷原子的方均根速度v，而方均根速度与原子的温度T满足方程:

因为BEC不满足高斯分布，所以测量的是BEC周边的冷原子温度. 如图15的含有BEC的3幅图，由于不是非常纯的BEC，所以底端都会有略热的冷原子分布，以这些冷原子做基础，高斯耦合，最后测量出玻色-爱因斯坦凝聚的温度.

(a) 5 ms的TOF，高斯耦合后，得到

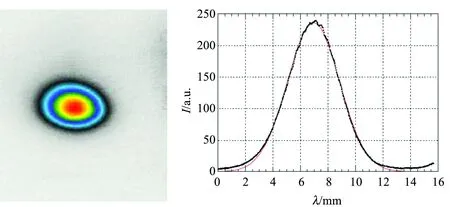
(b)34 ms的TOF，高斯耦合后，得到

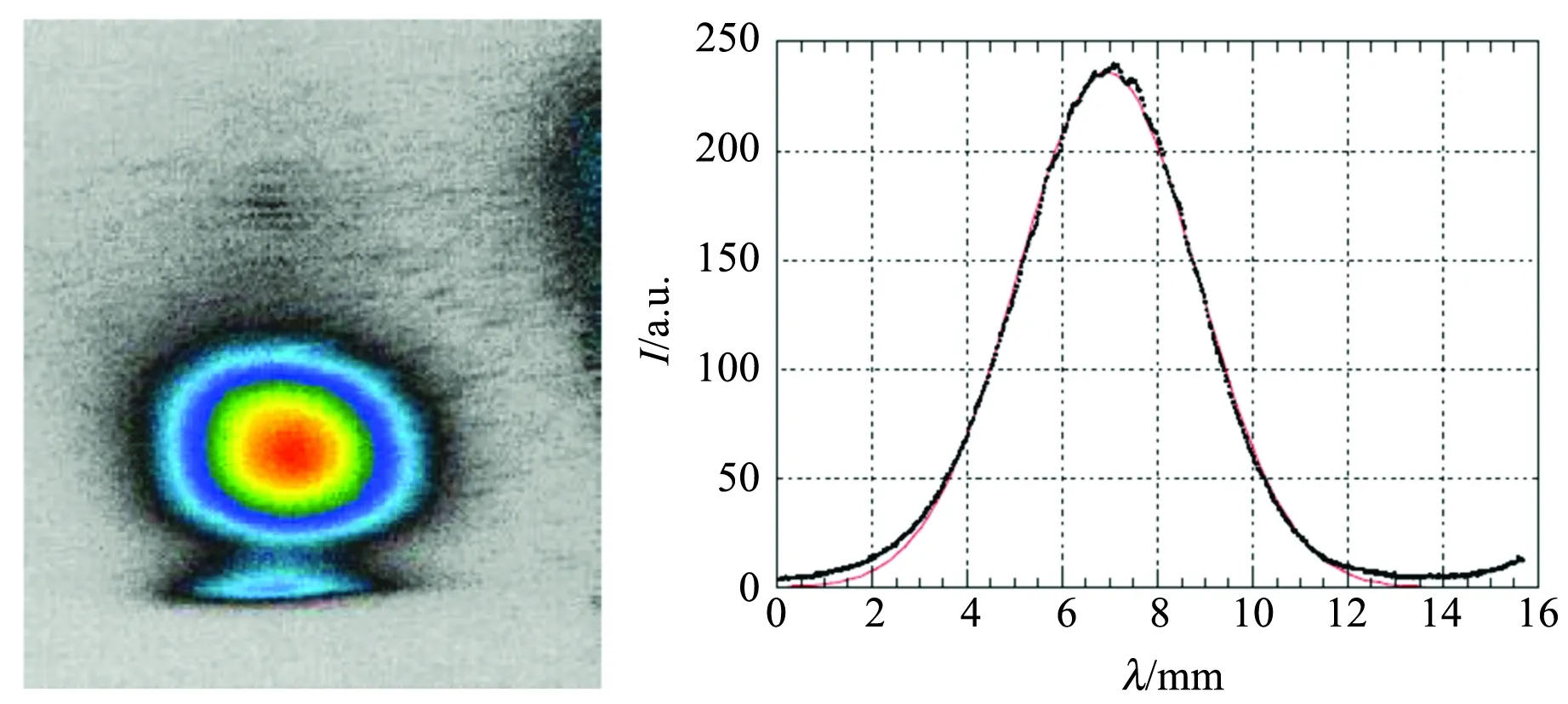
(c)44 ms的TOF，高斯耦合后，得到图32 吸收图

6.2 测量捕获原子的总数量

以Kathrin Luksch的论文为例来说明如何测量原子团数量[21]. 在实验中从吸收图CCD上得到图33，图33(a)为有原子团，中间暗影为原子团，光通过时，被吸收，所以显示出来. 图33(b)为没有原子的光的图像. 用图33(a)的图像减去图33(b)的图像，选择原子团的x轴和y轴做截面，用高斯耦合得到图34的x轴剖面和y轴剖面[20]. 根据文献[20]中的公式

即可计算原子的数量，式中Ax,y拟合振幅，η是量子效率，Г是自发辐射率，r是图像透镜的半径，R是原子团到透镜的距离，β是衰减因子，tp是探测时间，wx和wy是x和y平面的耦合的宽度.

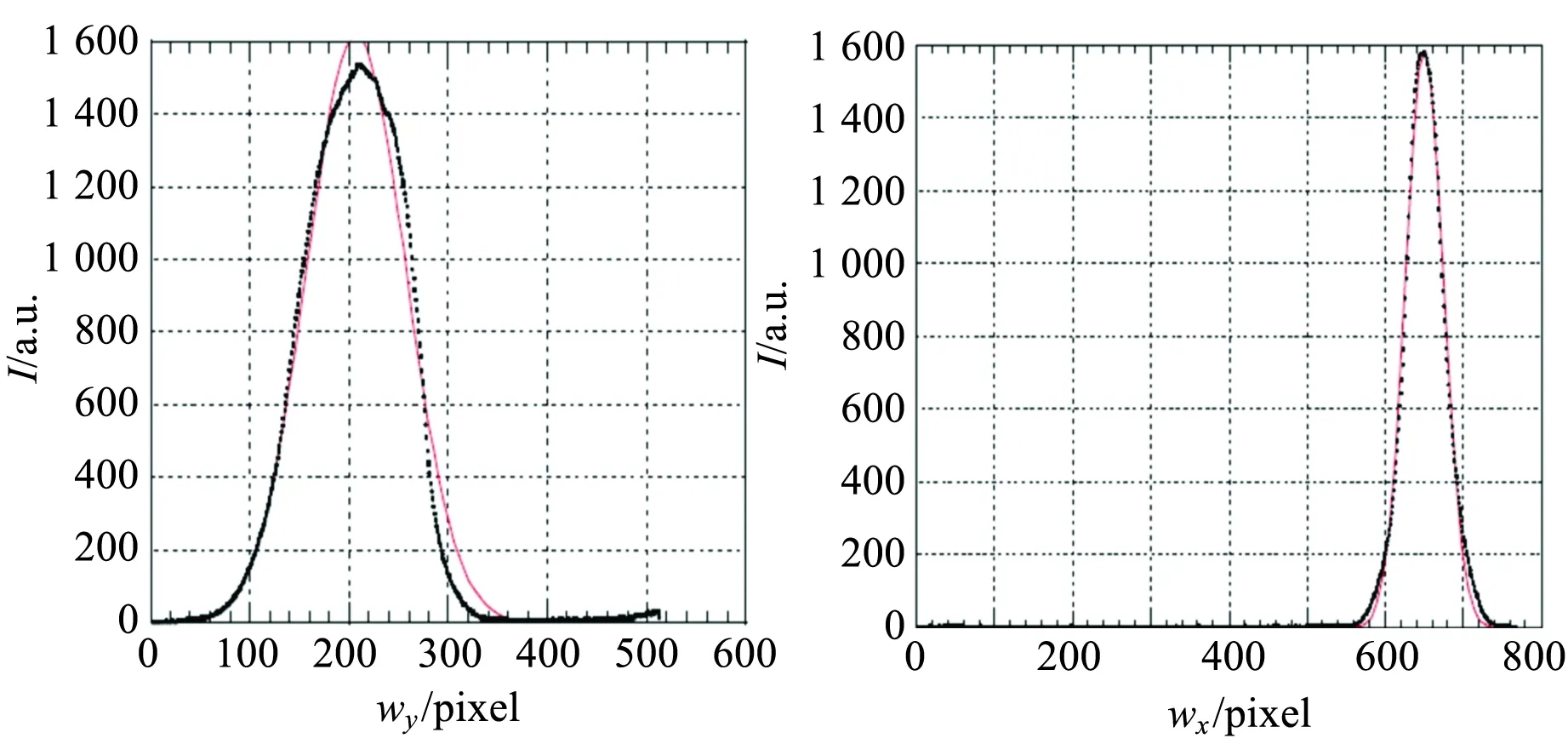
(a)y轴剖面图 (b)x轴剖面图图34 高斯耦合后的x轴、y轴剖面图

还可以用共振散射截面来算，因共振散射截面为

其中g取决于塞曼子状态和激光极化，而

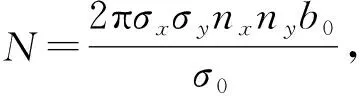
σx和σy分别为x和y方向的高斯耦合半径，nx和ny为x和y方向的像素，b0为原子团的共振处(失谐为0，δ=0处)的光学厚度. 基于此方法，得到图15和图23中MOT1和MOT2里的原子数量.

7 红失谐和蓝失谐光捕获冷原子的研究

由图29可以看出，红失谐光可以直接捕获冷原子(如图35所示)，而蓝失谐光无法直接捕获冷原子. 但是蓝失谐光可以形成环状结构来捕获冷原子，如图36所示[22].

2000年L. Khaykovich等人用实验论证了用旋转的蓝失谐来捕获原子[23]， 如图37～38所示. 用蓝失谐的光及2个AOM形成旋转光，从而捕获了冷原子，图38为不同旋转频率对应的捕获的冷原子的寿命.

(a) (b) (c)图35 红失谐光捕获冷原子

图36 蓝失谐光环状结构捕获冷原子

图37 蓝失谐光及2个AOM形成旋转光捕获冷原子

图38 不同旋转频率下捕获的冷原子寿命

8 冷原子的快速压缩法和玻色-爱因斯坦凝聚的绝热捷径

在做冷原子和BEC的实验时，发现快速让冷原子或BEC达到稳定状态的方法，磁场的变化为特定的曲线时，冷原子或BEC能从一个平衡态快速转到另一个平衡态.

8.1 冷原子的2个平衡态之间的快速最优过渡

我们演示了快速达到最终态的技术[24]，它的效果如同长时间慢慢地绝热转化. 实验用这种方法快速解压缩冷原子团，能在35 ms内，解压磁场15个量级. 跟标准的绝热解压过程相比，快了37倍的时间.

如图39所示，该磁场系统x,y,z的捕获频率分别为

图39 原子处在磁场中

变换磁场测得的z轴方向的磁场捕获频率随着时间的变化如图40所示.

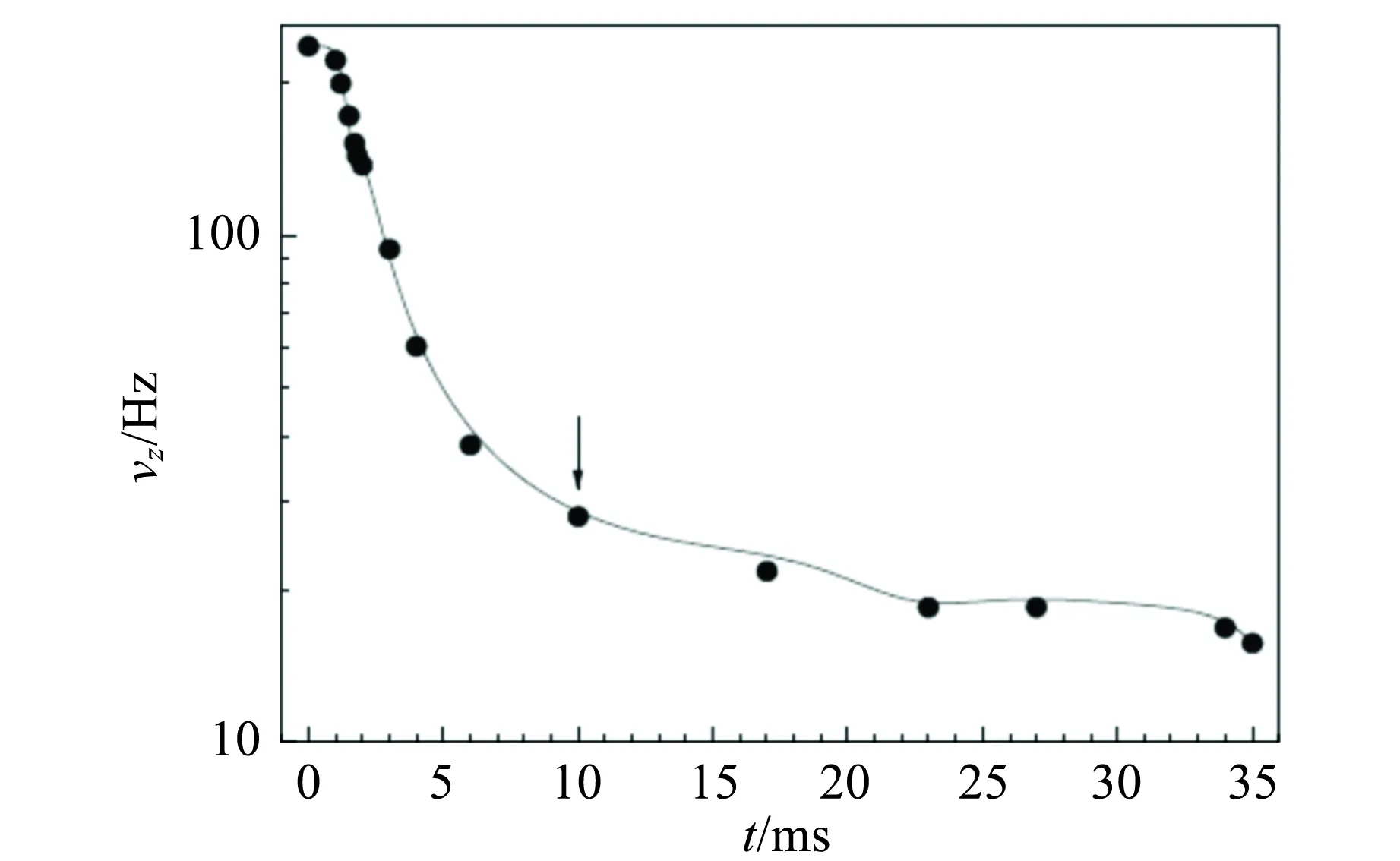
图40 z轴方向磁场捕获频率随时间的变化

实验结果如图41所示，center-of-mess 位置为zcm,z轴的原子团大小为σz. 绿色环状线为突然关断磁场后测得的原子团的震荡状况. 黑色圆球线为35 ms内线性关断磁场后原子团震荡状况. 红色的星型线为快速最优过渡法，在35 ms关断磁场后，原子震荡的状况. 而蓝色方框线为绝热6 s中线性缓慢关闭磁场后，原子团震荡的状况. 从图41可以看出，该技术在35 ms就能达到传统中6 s绝热过程所达到的结果. 从而实现短时间变换磁场，而能保持原子还是处于稳定绝热的状态.

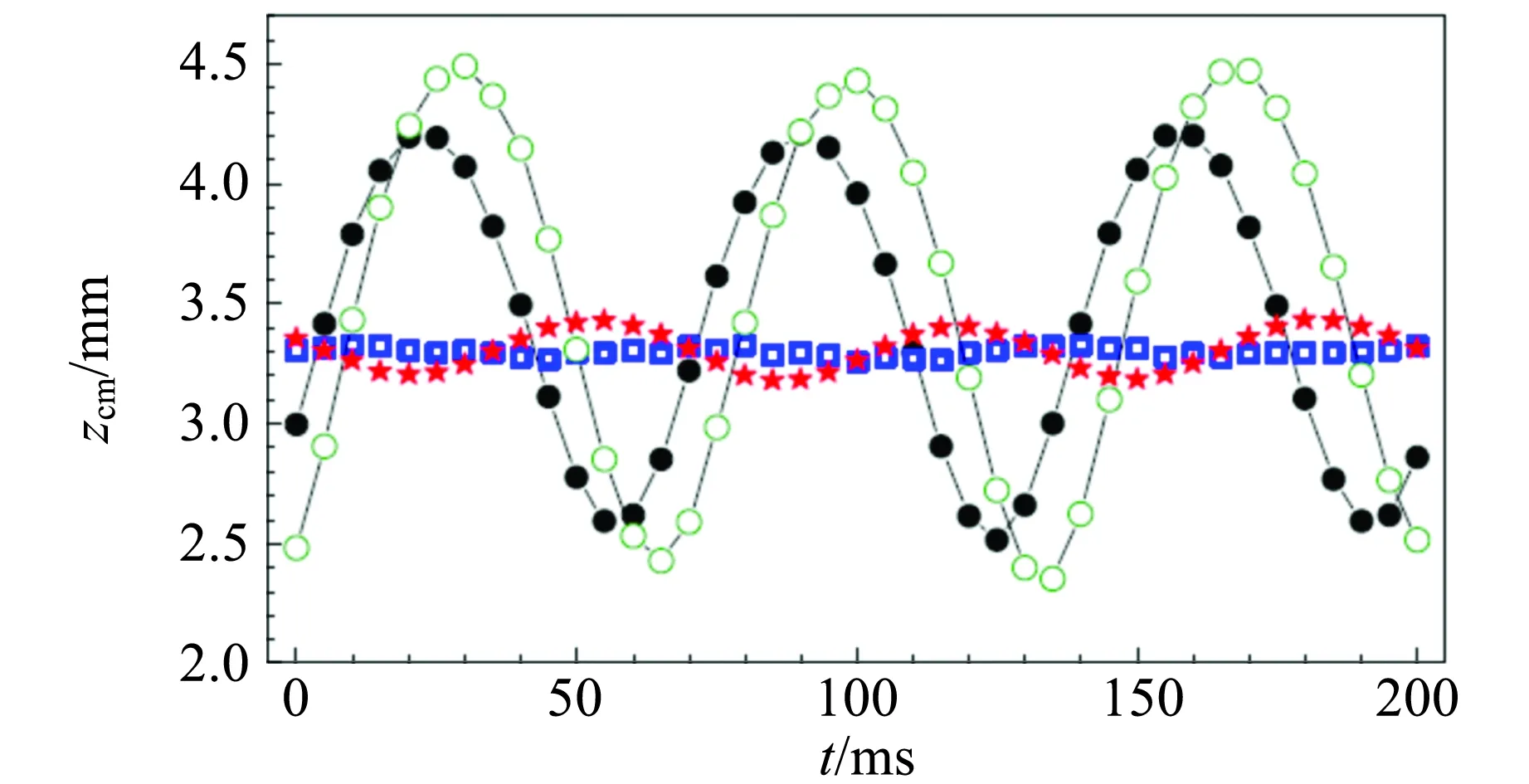
(a)

(b)图41 采用不同关断磁场方法后原子图的位置和大小的对比图

8.2 玻色-爱因斯坦凝聚的互动的绝热快捷方式

文献[25]提了3D玻色-爱因斯坦凝聚的快速解压缩法. 利用时间独立的gross-pitaevskii方程，展示了一个时间更短到达绝热终态的解决方案. 同时测量BEC和冷原子部分，证实了这种特定的捕获轨迹，对量子作用是有效的. 文献[25]中，用快速捷径解压3D BEC的harmonic捕获，来观察快速捷径法对BEC和它周围的冷原子团的作用.

图42显示了磁场线性解压与磁场快速捷径法解压实验结果的比较，(a)为30 ms磁场线性解压的过程中BEC的震荡变化；而(b)为30 ms快速捷径法的BEC的震荡变化.

图42 BEC的震荡变化

实验也测量了BEC的center-of-mass位置和宽高比R，如图43蓝色线对应于磁场突然关闭解压，黑色线为磁场在30 ms内线性关闭解压，而红色线为磁场30 ms绝热过程关闭解压.

(a)BEC的中心位置测量

(b)宽高比R的测量图43 BEC的center-of-mass位置和宽高比R

关于快速捷径绝热过程的理论可以参考文献[6，24-25].

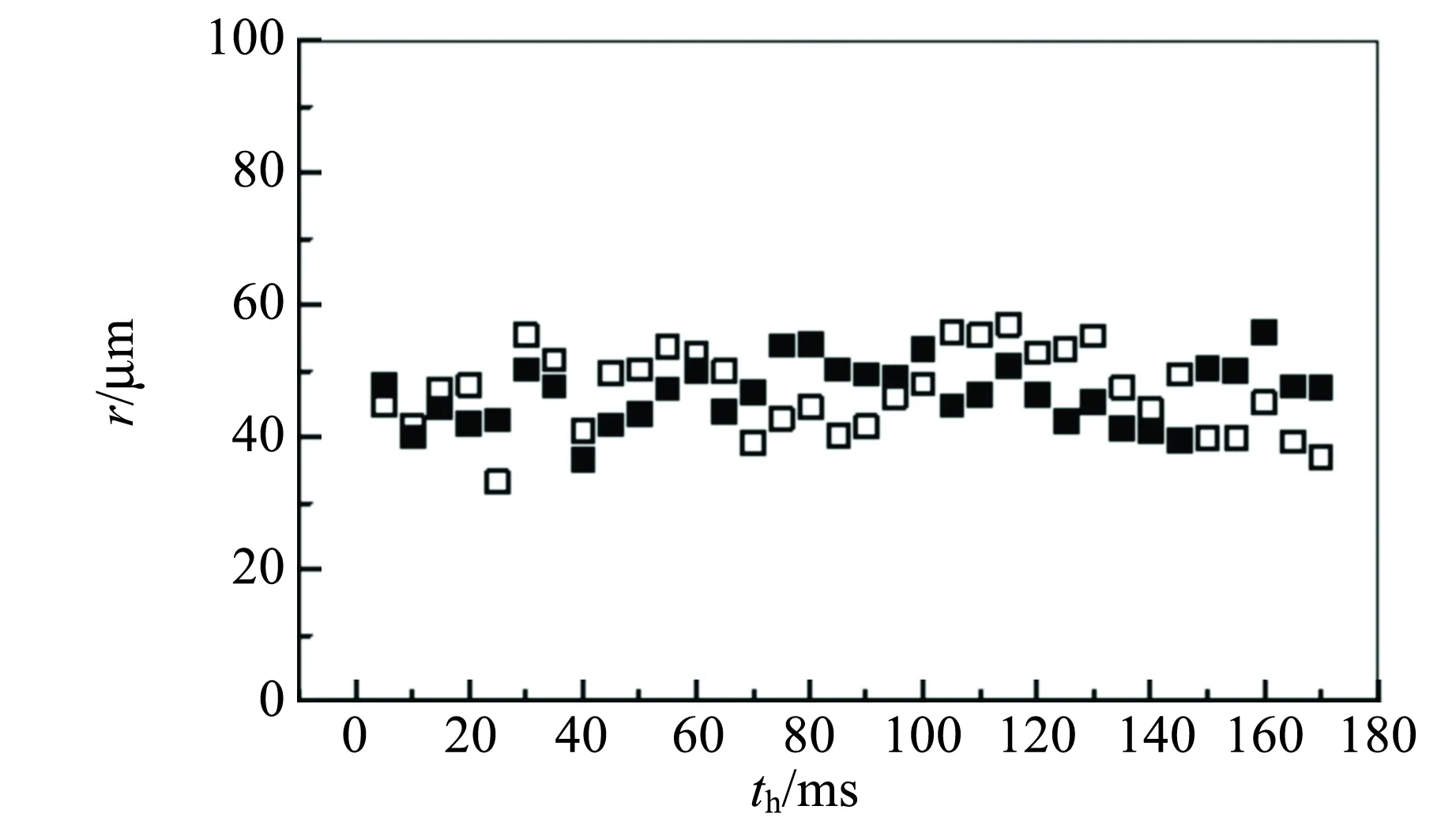
(a)BEC的震荡图

(b)BEC周围的残留冷原子团的测量图44 快速捷径方法对BEC及其周围冷原子团的测试

9 结束语

本文系统介绍了冷原子和玻色-爱因斯坦凝聚的历史、物理原理以及制备过程、实验搭建、实验方法、实验测量、磁场分布构造等，也介绍了几种蒸发冷却法，几种抵制磁场0点法，红失谐、蓝失谐捕获冷原子法，以及如何测量冷原子和BEC的温度、数量等. 最后介绍了我们所做的实验研究成果，使冷原子、BEC达到绝热稳定状态的快速方法. 随着量子信息技术的发展，冷原子,玻色-爱因斯坦凝聚在光学的研究中愈发显得重要. 尤其玻色-爱因斯坦凝聚，它奇特的物理特性，更使得很多量子研究得以实现突破性的进展.

致谢：感谢笔者在法国的同事Jean-Francois Schaff、指导教授Guillaume Labeyrie以及西北大学的指导教授John Ketterson, 是在他们的帮助和交流下，笔者能学习和了解许多宝贵的知识.

参考文献：

[1] Ketterle W. When atoms behave as waves: Bose-einstein condensation and the atom laser [J]. International Journal of Modern Physics B, 2002,16(30): 4537-4575.

[2] Bose S N. Plancks Gesetz und Lichtquantenhypothese [J]. Zeitschrift Fur Physik，1924，26：178-181.

[3] 百度百科.玻色-爱因斯坦凝聚态. https://baike.baidu.com/item/%E7%8E%BB%E8%89%B2-%E7%88%B1%E5%9B%A0%E6%96%AF%E5%9D%A6%E5%87%9D%E8%81%9A%E6%80%81/4191177?fromtitle=%E7%8E%BB%E8%89%B2%E2%80%94%E7%88%B1%E5%9B%A0%E6%96%AF%E5%9D%A6%E5%87%9D%E8%81%9A%E6%80%81&fromid=1846689,2018-04-07.

[4] 王增斌，张国万，韩军海. 量子工程导论[M]. 北京：中国原子能出版社，2017.

[5] Voigt D, Wolschrijn B T, Petra S J H, et al. Optical generation of coherent matter waves [DB/OL]. http://www.science.uva.nl/research/aplp/ewm/poster.htm,2018-04-05.

[6] Jean-François Schaff. Shortcuts to adiabaticity for ultracold gases，de l′Universite de Nice-Sophia Antiplis, 2011.

[7] Guery-Odelin D, Soding J, Desbiolles P, et al. Strong evaporative cooling of a trapped cesium gas[J]. Optics Express , 1998, 2(8):323-329.

[8] Guerin W, Riou J F, Gaebler J P, et al. Guided Quasicontinuous Atom Laser [J]. PRL, 2006, 97:200402.

[9] Madison K W, Chevy F, Wohlleben W, et al. Vortex Formation in a stirred Bose-Einstein Condensate[J]. PRL, 2000,84:806.

[10] Andrews M R, Townsend C G, Miesner H J, et al. Observation of Interference between Two Bose Condensates [J]. Science, 1997,275(5300):637-641.

[11] Greiner M， Regal C A, Jin D S. Emergence of a molecular Bose-Einstein condensate from a Fermi gas [J]. Nature, 2003, 426(6966):537.

[12] https://www.wznav.com/article/24628404/. 2018-04-08.

[13] 韩殿君. 铷原子之玻色爱因斯坦凝聚[J]. 物理,2005(4):384.

[14] Hung C L, Zhang X, Gemelken N, et al. Accelerating evaporative cooling of atoms into Bose-Einstein condensation in optical traps [J]. Physical Review A, 2008,78,011604(R) .

[15] Jones M P A. Bose-Einstein Condensation on an Atom Chip [D]. Brighton: University of Sussex, 2002.

[16] Daniel Adkins Paseltiner. Progress towards Bose-Einstein condensation on an atom chip as a functional testbed for experiments aboard the orbital NASA Cold Atom Laboratory[D]. Lewiston: Bates College, 2016.

[17] Barr Iain. Investigating the Dynamics of a Bose Einstein Condensate on an Atom Chip [D]. London: Imperial College London, 2015.

[18] Esslinger T, Bloch I, Hänsch T W, Bose-Einstein condensation in a quadrupole-Ioffe-configuration trap [J]. Physical Review A，1998,58, R2664.

[19] Naik D S, Raman C. Optically plugged quadrupole trap for Bose-Einstein condensates[J]. Phys. Rev. A,2005,71, 033617.

[20] 韩百增. 銣原子玻色-爱因斯坦凝聚之亚普磁阱[D]. 嘉义:台湾国立中正大学， 2002.

[21] Luksch Kathrin. Measurement of the Number of Atoms in a Magneto-Optical Trap Using Absorption Imaging [D]. 2012.

[22] Rudolf Grimm, Matthias Weidemuller. Optical Depole Traps for Neutral Atoms [J]. Advances in Atomic, Molecular, and Optical Physics, 2008,42(2000), 95-170.

[23] Khaykovich L, Friedman N, Ozeri R, et al. Compression of cold atoms to very high densities in a novel rotating-beam blue-detuned optical dipole trap [J]. Physical Review A, 2000,61, 031403(R).

[24] Schaff Jean-Francois, Song Xiao-Li, Vignolo Patrizia, et al. Fast optimal transition between two equilibrium states [J]. Physical Review A, 2010, 82:033430.

[25] Schaff Jean-Francois, Song Xiao-Li, Capuzzi Pablo, et al. Shortcut to adiabaticity for an interacting Bose-Einstein condensate[J]. EPL, 2011, 93: 23001.