基于数据敏感度自适应的SDT改进算法*
张涵笑,慕福奇,吕欣岩
(1. 中国科学院物联网研究发展中心,江苏 无锡 214135;2. 中国科学院大学 微电子学院,北京 100049;3. 江苏中科羿链通信技术有限公司,江苏 无锡 214135)
0 引言
随着物联网技术的飞速发展与普及,人们身边越来越多的数据被监测和记录。例如使用较为广泛的环境信息监测传感器,在工厂、医院、运输、家庭等各种场景都有应用。这类环境监测数据包含温度、湿度和PM2.5浓度等多种类型,这些数据的持续上传形成了海量的历史时序数据。如何高效地存储这些数据是物联网技术研究的重要内容,许多研究者从数据压缩入手以减少数据占用的存储空间。
旋转门压缩算法(Swinging Door Trending,SDT)是常用的时序数据压缩算法[1-3]。研究人员针对各种实际使用场景对传统的SDT算法提出了不同的改进方案。如增加强制记录限来解决变化幅度较小的数据很长时间不被保存的问题[4];保存两记录点之间的原始数据的逼近线段来代替记录原始数据点以提高压缩比[5];预先对原始数据进行平滑和去噪处理,然后再使用SDT算法进行压缩以提高压缩率[6];将SDT算法与无损压缩算法结合起来,进一步提高压缩率[7];根据数据变化幅度来动态调整压缩偏差以提高压缩率;记录对压缩精度影响最大的数据点来提高压缩精度[8]。这些改进基本都是根据应用场景的不同,在运算性能、压缩率和压缩精度三项指标间进行权衡,以达到最适合应用场景的压缩方案。以上方法或增加数据处理步骤,或引入了复杂的数学计算,在提高压缩率或压缩精度的同时也增加了算法复杂度,而对于海量数据的处理算法是否高效尤为重要。这些方法对所要处理的所有数据一视同仁,均使用相同的压缩策略。而现实中,如对环境监测数据,往往比较关心高于或低于某一限值的异常值,对于数据在正常值附近波动并不那么敏感。在这种情况下,对所有数据使用相同的压缩策略是不合适也不高效的。本文提出一种基于数据敏感自适应的SDT改进算法,根据数据的敏感程度使用不同的压缩策略,能更好地适用这种场景。
1 旋转门压缩算法简介
旋转门压缩算法是一种用于时序数据压缩的有损压缩算法[9-11]。其原理如图1所示。

图1 标准SDT算法示意图
A点为数据开始记录点,在A点上方和下方分别取两点A+和A-,横坐标与A点相同,纵坐标与A点相差一个容差参数ΔE。从A点开始向后遍历数据,分别从A+和A-点向下一数据点B画线,得到A+B与A-B两扇门,∠AA+B与∠AA-B为两扇门的夹角。用同样的方式去处理后面的数据点,两扇门的角度只能增大不能减小,且要保证两夹角之和不能超过180°。如对于数据点C,需要将下面这扇门打开更大的角度来包含住C点,上面那扇门不变。因为两扇门夹角不超过180°,所以本压缩周期继续。直到处理到E点时,此时上面的那扇门为A+D,要想包含E点,需要把下面的那扇门打开至A-E的位置。这样两扇门的夹角和就会超过180°,因此需要结束本次压缩周期,记录上一数据点D作为此周期的结束点,并将E点作为起点开始新的压缩周期。使用这样的方式,只记录了A、D两点的值,舍弃了中间的数据点B、C,达到压缩数据的目的。
2 改进的算法
通过研究标准SDT算法,本文提出了一种基于数据敏感度自适应的SDT改进算法(Sensitivity Adaptive Swinging Door Trending,SASDT)。与算法相关的参数及表示形式如下:
ΔE:容差参数;
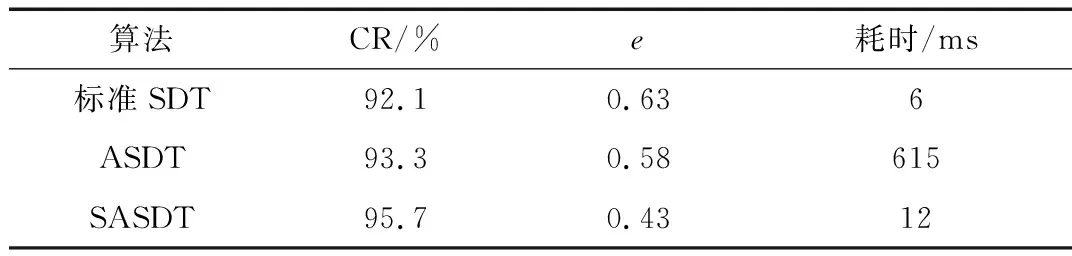
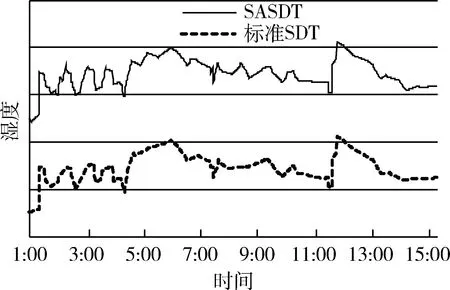
k:ΔE的调整系数(0 ΔEL-min:宽松标准容差范围下限; ΔEL-max:宽松标准容差范围上限; ΔES-min:严格标准容差范围下限; ΔES-max:严格标准容差范围上限; Smax:单个压缩周期的最大步长; S:本次压缩周期的步长; S1:上次压缩周期的步长; M:敏感数据区间; T:当前压缩周期的压缩类型,类型分为敏感数据压缩与非敏感数据压缩两类。 在传统的旋转门压缩算法中,ΔE是决定压缩率与压缩精度的重要参数。本文基于两个方面的因素来动态地调整ΔE的值,一是数据点的敏感程度,二是数据变化波动大小。 数据的敏感度区间可由用户灵活设置,使得用户关心的数据具有较小的压缩误差。原始数据敏感度较低时使用ΔE较大的宽松标准,对高敏感度的原始数据使用ΔE较小的严格标准,以此来提高低敏感度数据的压缩率和高敏感度数据的压缩精度。在宽松或严格的不同标准范围内,根据数据的波动大小来自动调整ΔE,做到进一步精准压缩。 因为旋转门压缩算法的压缩原理就是将变化波动小于某一值的一组连续数据用一条线段来拟合表示,所以一次压缩周期的步长就表示了数据波动相对稳定的连续长度。可以用步长来表征当前数据的变化波动趋势,当步长较大时说明数据具有长时间稳定的趋势,反之则说明数据波动较大。在改进的算法中,数据当前压缩周期的步长大于上一周期步长时说明数据波动在趋于稳定,以系数k按比例增大ΔE可取得更好的压缩率;反之则说明数据波动趋于变化,以系数k按比例减小ΔE来降低压缩误差。 算法:基于数据敏感度自适应的SDT改进算法 输入:原始监测时序数据 输出:压缩后的时序数据 步骤1:读取待压缩数据,根据数据是否在敏感区间M内,判断数据是否为敏感数据。若数据敏感度与当前压缩类型一致,则进行步骤2;若不一致,则进行步骤5。 步骤2:判断当前压缩周期步长是否超过最大步长Smax,若未超过则进行步骤3,若超过则进行步骤4。 步骤3:根据旋转门算法判断待压缩数据是否可以被当前压缩周期压缩。若可以,则本压缩周期步长加1,进行步骤6;否则跳至步骤4。 步骤4:记录上一个原始数据作为本压缩周期的结尾数据。根据S与S1的比较结果来调整ΔE。当S≥S1时,ΔE=ΔE*(1+k);当S 步骤5:记录上一个原始数据作为本压缩周期的结尾数据。根据当前数据的敏感度旋转相应的压缩标准,将使用的压缩标准类型赋值给T。重置参数ΔE,若为宽松标准,则ΔE=(ΔEL-min+ΔEL-max)/2;若为严格标准,则ΔE=(ΔES-min+ΔES-max)/2。将S1和S初始化为1。使用这些参数,从当前数据开始,启动新的压缩周期,进行步骤1。 步骤6:判断是否还有新数据,若有则执行步骤1,若无则记录本压缩周期首尾数据,结束压缩周期,退出。 基于数据敏感度自适应的SDT改进算法流程图如图2所示,本算法相比标准的SDT算法主要有两方面改进:一是根据数据敏感度的不同,采用不同的容差标准进行压缩,可以使得用户敏感的数据具有较低的压缩误差,同时从非敏感数据部分得到压缩率的补偿;二是根据数据的波动情况动态地调整容差,可以进一步提高压缩率。 图2 改进的算法流程图 为了验证改进算法的有效性,本文使用Java语言编写实现了标准SDT算法、文献中最新研究的自适应SDT算法(Adaptive Swinging Door Trending,ASDT)[6]和本文提出的基于数据敏感度的自适应SDT算法(SASDT),分别使用这三种算法处理相同的数据,以比较算法的性能。 本文将压缩率CR、均方根误差e以及压缩耗时作为衡量算法性能的三个指标[12]。计算公式如下: 其中,m是压缩删除的数据量,n是原始数据量。 待压缩的原始数据来源于实际环境监测数据,包括温度数据和湿度数据。选取10组监测数据,每组数据量为10 000个。标准SDT算法中参数为:容差范围ΔE=1.5,最大步长Smax=100;在ASDT算法中,容差参数ΔEmin=1,ΔEmax=2,最大步长Smax=100;在SASDT算法中,调整系数k=0.2,宽松标准容差参数ΔEL-min=1.5,ΔEL-max=3,严格标准容差参数ΔES-min=0.5,ΔES-max=1,最大步长Smax=100,敏感数据区间根据数据类型而定。对多组数据执行压缩算法后,得到性能平均结果如表1所示。 表1 各算法压缩性能结果比较 从结果可以看出,相较于标准SDT算法,SASDT算法压缩率有小幅提升,压缩误差减小了32%,效果明显;与ASDT算法比较,SASDT算法在压缩率与压缩误差上也均得到优化。 SASDT算法复杂度与标准SDT算法相比,仅仅是在处理每个数据点时进行一次比较来判断数据的敏感度。而且调整容差的依据也是通过压缩步长来判断的,不需要额外增加计算和统计。因此,改进算法的时间复杂度与标准SDT算法的复杂度差别不大,从表1中的结果也可以看出这点。而ASDT由于增加了数据处理步骤且引入了复杂的数学计算,因此在运行时长上耗时较大,大约是SASDT算法的50倍。在海量数据的处理中,算法的运行效率尤为重要。 图3 压缩恢复数据对比图 从压缩数据中选取一段进行还原并绘制折线图,比较标准SDT算法与SASDT算法压缩数据的还原情况,结果如图3所示。从图3明显可以看出,在1:00~3:00和5:00~9:00这两个时间段中SASDT算法的压缩精度更高,数据还原更准确,保留了很多标准SDT算法中没有的变化趋势与细节。 本文提出的基于数据敏感度自适应的SDT改进算法已应用在一个实时监测系统中,使用效果如图4所示。将系统中的历史监测数据进行压缩,可大大减少系统所需的存储空间。由于算法复杂度低,运行效率很高,能快速高效地对大量历史数据进行压缩。同时数据解压简单高效,也能满足系统实时查询历史数据的要求。数据还原能够反映原始数据的变化状态,而且对于敏感数据具有较高的还原精度。系统可以根据需要动态地调整敏感数据区间,也可以灵活地更改严格和宽松的容差范围,以满足系统需求的同时取得最好的压缩效率与压缩精度。目前,该系统已投入实际使用,数据压缩及解压功能运行正常,用户反馈良好,改进算法的有效性与稳定性得到了进一步验证。 图4 实际应用效果图 本文通过对应用场景需求的分析以及对标准SDT算法的研究,从数据敏感度和动态调整容差两个方面入手,提出并实现了基于数据敏感度自适应的SDT改进算法。该算法针对原始数据敏感度不同的问题,采用精度不同的容差标准,保证了用户关心的数据的压缩精度;同时,根据相邻压缩周期的步长变化,动态调整下一压缩周期的容差值,这样可以减少波动较小的 平稳数据的记录量,进而提高数据压缩率。该算法复杂度低,没有增加复杂的数学计算,具有很高的效率。经过性能对比及实际的使用,算法的有效性得到验证,可灵活高效地应用于各种环境中监测数据的压缩场景。 [1] 杨冠杰, 李悦. 工业实时数据压缩算法的分析[J]. 自动化与仪器仪表, 2016(8):214-215. [2] 刘佳宝, 梁奕, 方俊. 一种过程数据有损压缩比的动态控制方法[J]. 计算机工程与应用, 2013, 49(8):138-141. [3] 赵旭东, 丁杰雄, 边志远,等. SDT改进算法在数控系统监控平台中的应用[J]. 制造技术与机床, 2014(10):155-159. [4] Li Xinli, Qiu Hongkai, Zhu Yaochuan. Research and design of lossy compression algorithm in embedded real-time database[C]// Proceedings of the Second International Conference on Mechatronics and Automatic Control. Springer International Publishing, 2015:1027-1034. [5] 邢锐, 祁奇, 郑滔. 改进的SDT算法[J]. 计算机工程与设计, 2013, 34(2):515-518. [6] 张宗华, 叶志佳, 牛新征. 面向监测数据压缩的自适应SDT算法[J]. 中国测试, 2017, 43(2):104-108. [7] 张炜, 王英洁, 邬蓉蓉. 面向油中溶解气体监测时序数据压缩的改进方法[J]. 电力建设, 2017, 38(5):98-104. [8] 邱红锴. 用电及能效信息采集系统嵌入式实时数据库关键技术研究[D]. 北京:华北电力大学, 2015. [9] 于松涛, 王晓琨, 赵利强,等. 基于容差动态调整的旋转门(SDT)改进算法[J]. 北京化工大学学报(自然科学版), 2013, 40(3):109-113. [10] 曲奕霖, 王文海. 用于过程数据压缩的自控精度SDT算法[J]. 计算机工程, 2010, 36(22):40-42. [11] Chen Gang, Li Li. An optimized algorithm for lossy compression of real-time data[C]// IEEE International Conference on Intelligent Computing and Intelligent Systems. IEEE, 2010:187-191. [12] 宁海楠. 一种基于SDT算法的新的过程数据压缩算法[J]. 计算机技术与发展, 2010, 20(1):25-28.2.1 算法思想
2.2 算法步骤

3 算法分析
3.1 评价指标

3.2 对比分析
3.3 应用实例

4 结论

