高速降噪差分混沌键控系统

张 刚, 郝怡曼, 张天骐

(重庆邮电大学信号与信息处理重庆市重点实验室, 重庆 400065)

0 引 言

由于混沌[1-4]信号特殊的性质,使其成为了无线通信领域众多研究机构的研究对象。在过去的几十年里,众多学者提出了各种混沌通信系统的相干和非相干算法。相干检测由于需要同步混沌载波,使其应用受限。基于相干检测的缺点,使差分混沌键控(differential chaos shift keying, DCSK)[5-6]在混沌通信系统发展过程中成为最值得考虑的方案。究其原因是DCSK系统在不需要混沌载波同步和信道状态估计的情况下依然可以在接收端恢复出传输的信息。此外,DCSK有着更好的抗多径衰落的能力,更适合超宽带传输。然而,传统的DCSK系统传输效率低下,安全性低等问题限制了它的应用。由于DCSK系统存在限制其应用的缺点,众多学者也针对其进行了各种改进。文献[7]提出了多阶相关延迟键控(correlation multi delay shift keying, CMDSK)系统,该系统将传统的加法器改为减法器,并将参考信号与延迟不同时间的数据信号做减法运算,从而提高数据传输速率。文献[8]通过引入Hilbert变换使得数据信号与参考信号之间达到完全正交,从而可以连续传输2 bit信息,该方式是以牺牲调制复杂度为代价来换取提高传输速率的。文献[9]中的两个正交信号是通过时间反转操作得到的,传输速率并没有得到提高,但降低了误码率(bit error rate, BER)。此外,为提高DCSK传输速率提出了文献[10]和文献[11]。文献[12]引入多载波技术从而提高了DCSK系统的安全性,文献[13]在文献[12]的基础上进行改进,从而提出了一种新型的多载波差分混沌键控(multi-carrier DCSK,MC-DCSK)系统,在该系统中摒弃了常用的RF延时线,在频谱利用率方面得到了提高同时降低了能耗。文献[14]提出了通过Walsh码来区分参考时隙和数据时隙的码移位差分混沌键控(code-shifted DCSK,CS-DCSK)系统。文献[15]提出了改进型的CS-DCSK系统,采用共用参考时隙的方式将Nbit信息传输在同一帧内,这种方式提高了传输效率。文献[16]提出了高效差分混沌键控(high-efficiency DCSK,HE-DCSK)系统,在该系统里通过交叉参考的方式传输2 bit信息,通过前一帧的参考时隙来解调,提高了参考时隙的利用率。文献[17]提出了参考调制差分混沌键控(reference modulated DCSK,RM-DCSK)系统是将相邻的时隙相互作为各自的参考信号,从而使得传输效率得到提高。

为了进一步提高数据传输速率,本文提出了一种高速降噪的差分混沌键控系统(high rate noise reduction differential chaos shift keying, HRNR-DCSK)。在该系统中,一帧中的所有数据信号共用一个参考信号,同时参考时隙的长度会随着一帧中传输数据比特的增加而降低。在接收端采用移动平均滤波器,使其通过降低噪声方差的方式提高系统的性能。

1 基于混沌的非相干通信系统

1.1 DCSK通信系统

在DCSK系统的调制中,第1个时隙传输一段混沌序

列作为参考时隙,第2个时隙传输被调制了数据的混沌序列作为数据时隙。若传送的是+1,则参考序列就等于数据序列;若传送的是-1,则将反向的参考序列作为数据序列进行传送。DCSK系统的扩频因子定义了用来传输比特的混沌样本的数量,即为2β(β为整数)。此外,DCSK系统的比特周期为:TDCSK=2Tb=2βTc(Tc为码片时间)。在DCSK系统调制器的输出端,第i个比特间隔的信号可以表示为

(1)

式中,xi,k是作为参考时隙的混沌序列；xi,k-β是xi的延迟信号。

为了解调传输的信息,将接收到的信号与其延迟信号进行时间长度为Tb(Tb=βTc)的相关求和运算,接收端对其计算后的结果进行判决。DCSK系统在信道中传输时参考时隙和数据时隙都会受到噪声的影响,同时受到噪声破坏的参考信号和数据信号在接收端进行相关运算致使DCSK系统的性能恶化。这样将会导致DCSK系统在未来的超宽带通信应用中受限。DCSK系统发射机和接收机结构分别如图1、图2所示。

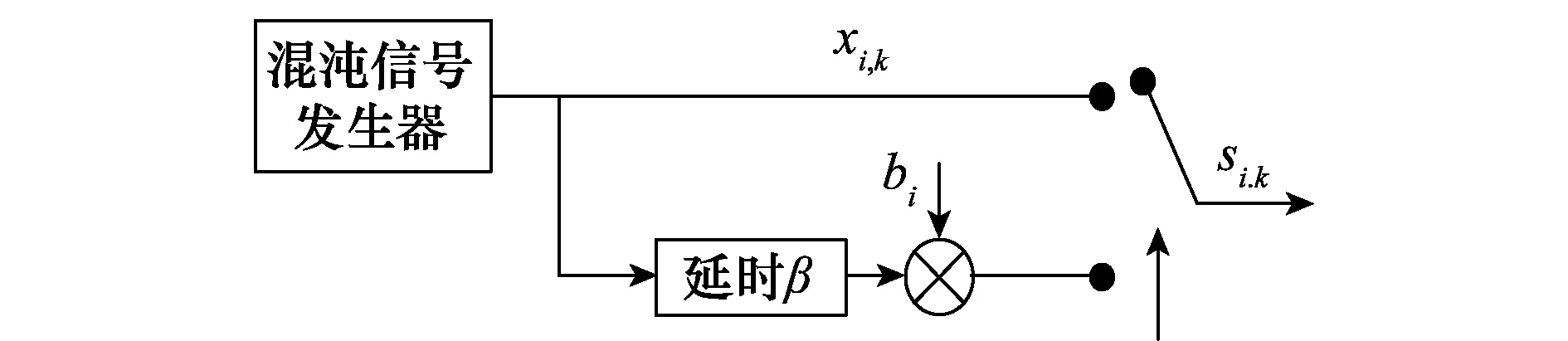
图1 DCSK系统发射机结构Fig.1 DCSK transmitter

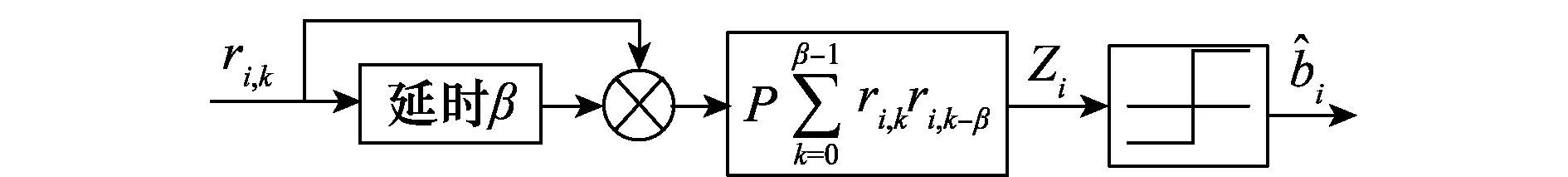
图2 DCSK系统接收机结构
Fig.2 DCSK receiver

1.2 HRNR -DCSK通信系统

传统的DCSK系统若传输Nbits数据则需要N个帧,即N个参考时隙和N个数据时隙。而HRMR-DCSK系统传输Nbit数据只需要一个参考时隙,同时参考时隙的长度是原来长度的1/N,即Nbit的数据传输时共用一个参考信号,不同的数据信号之间通过不同的Walsh码来区分，两种系统的帧结构如图3所示。

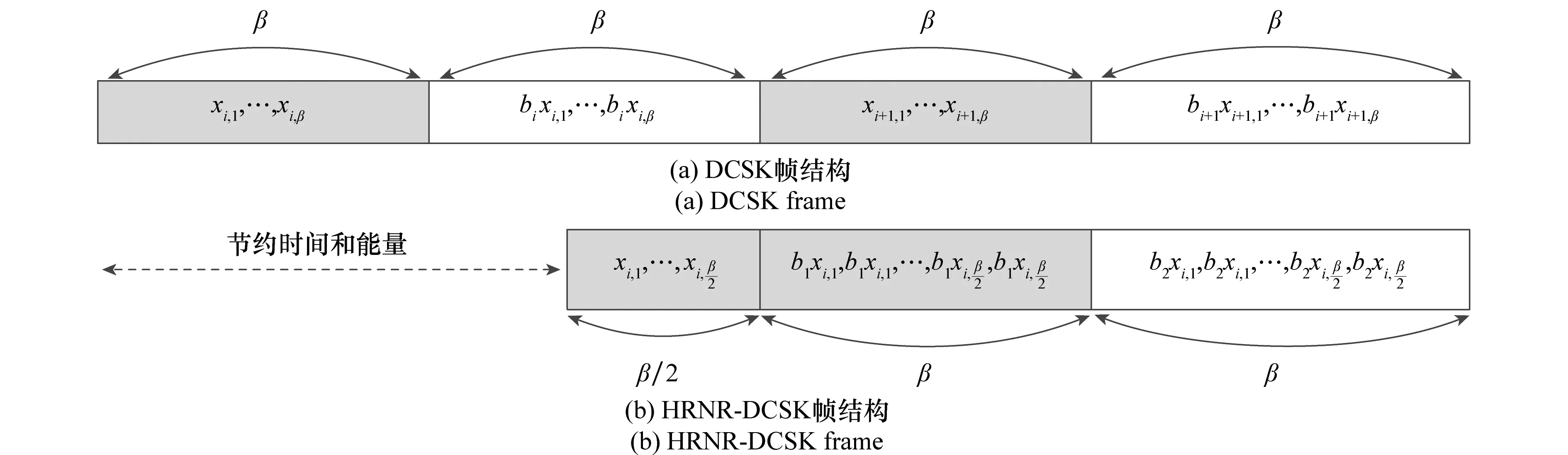
图3 HRNR-DCSK系统和DCSK系统的帧结构Fig.3 HRNR-DCSK frame and DCSK frame

同时在接收端采用移动平均滤波器进行滤波,使得通过降低噪声的方差来提高系统的性能。HRNR-DCSK系统传输Nbit数据的时间由DCSK系统的2Nβ变为了(N+1/N)β,由图3(a)和图3(b)可以看出,HRNR-DCSK系统的数据传输速率比DCSK系统得到了提高(图中以传输2 bit为例)。

图4给出了HRNR-DCSK系统的发射机结构。

图4 HRNR-DCSK系统的发射机结构Fig.4 HRNR-DCSK transmitter

HRNR-DCSK系统的原理是混沌信号发生器产生并发送一段长度为β/N的混沌序列,接下来的每一支路都将这段长度为β/N的混沌序列和一个N×N维的Hadamard矩阵的某一行进行克罗内克积运算,然后将经过运算后的混沌序列调制上不同的信息,最后分别进行发送。其中,图中的符号Ο是克罗内克积运算。则第i帧的发送信号可以表示为

(2)

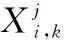
当同时传输Nbit数据时,传统DCSK系统所需要的传输时间为TDCSK=2NβTc,而HRNR-DCSK系统所需要的时间为THRNR-DCSK=(N+1/N)βTc。HRNR-DCSK系统相较于DCSK系统所提高的数据传输速率可以表示为

(3)

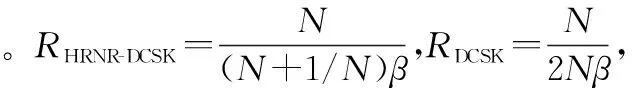
(4)

同理，HRNR-DCSK系统比DCSK系统所节约的比特能量可以表示为

(5)

式中，ED是HRNR-DCSK系统比传统DCSK系统所节约的比特能量百分比。

(6)

(7)

化简式(7)可得

(8)

将式(6)和式(8)代入式(5)可以得到

(9)

图5给出的是HRNR-DCSK系统的接收机结构。

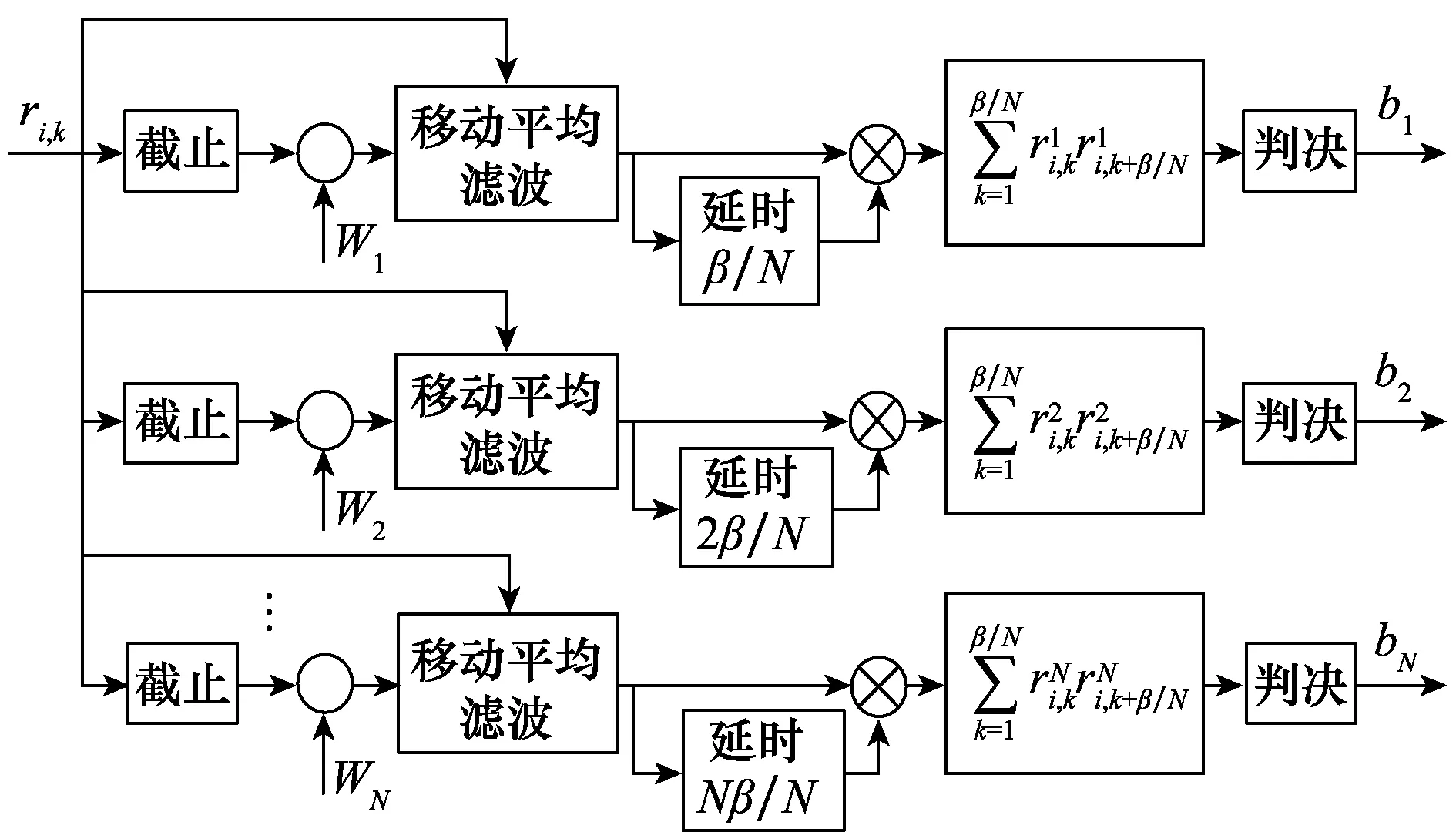
图5 HRNR-DCSK系统接收机结构Fig.5 HRNR-DCSK receiver

接收机的原理是当信号到达接收端时接收机将接收信号的参考时隙分别与各组Walsh码进行克罗内克积运算,然后将参考信号和数据信号依次通过移动平均滤波器,对每一段相同的采样信号取平均,最后进行相关运算及门限判决。其中,图中的符号Ο是克罗内克积运算。

文中采用两条独立路径的瑞利衰落信道(Rayleigh fading channel， RFC),信道模型如图6所示。

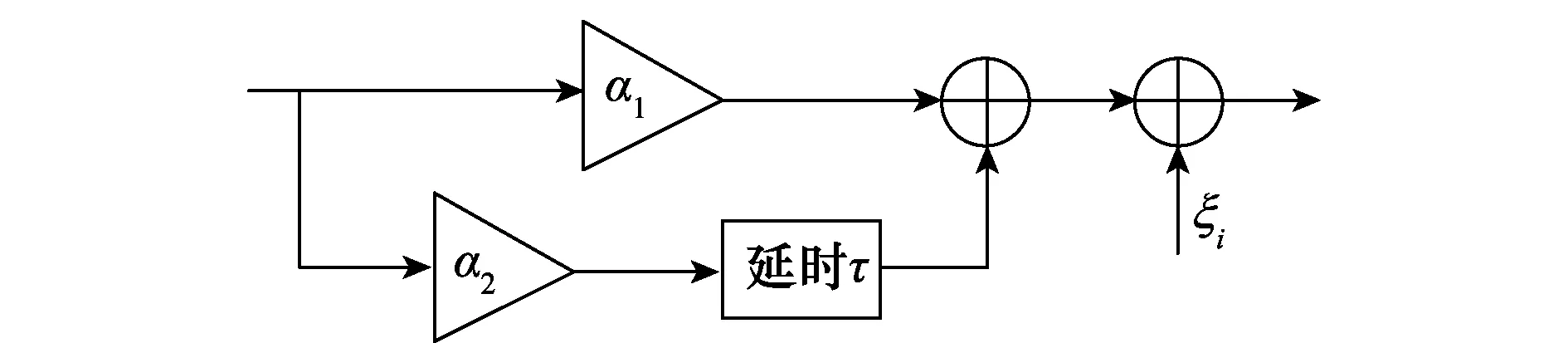
图6 RFC模型图Fig.6 Model of the RFC

其中α1和α2是两个独立的RFC的信道参数,τ是两个独立信道之间的延迟,信道参数α服从瑞利分布,即其概率密度函数可以表示为:f(α|σ)=(α/σ2)e-α2/2σ2(σ是瑞利分布的系数,σ>0),ξi是均值为零,方差为N0/2的高斯白噪声。则通过图6中的信道模型传输后接收端接收到的信号ri,k可以表示为

ri,k=α1si,k+α2si,k-τ+ξi,k

(10)

在以下的分析中,假设信道的延迟远远小于参考时隙的长度,即0<τ≤βTc/N。为了数学推导的方便性,假设码片时间Tc=1,基于以上的说明在第i帧(为了不失一般性i≥1)的相关器输出可以表示为

(11)

对式(11)进行展开,最终得到

(12)

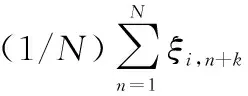
通过式(12)可以得到信息比特为

(13)

由于混沌序列的互相关性较低,所以混沌序列的有效长度β/N在较大时可以近似为

(14)

2 误码性能分析

(15)

E[I]=E[N1]=E[N2]=E[N3]=0

(16)

(17)

var[I]=0

(18)

(19)

(20)

(21)

(22)

式中,E[·]表示数学期望运算；var[·]表示数学方差运算。

采用高斯近似法,根据中心极限定理系统的BER可以表示为

(23)

进一步表示为

(24)

将式(21)和式(22)代入式(24)可得

BER(α1,α2)=

(25)

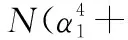
(26)

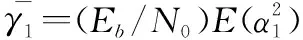
(27)

若令γb=γ1+γ2,则γb服从以下分布,即

(28)

由式(26)和式(28)可得HRNR-DCSK系统在多径RFC中的BER公式为

(29)

当信道参数α1=1,α2=0时,HRNR-DCSK系统在AWGN信道下的BER可以表示为

(30)

由式(26)和式(30)可以看出,HRNR-DCSK系统在AWGN信道中的BER性能主要与比特信噪比(bit signal to noise ratio, BSNR)Eb/N0、扩频因子β及每一帧所要传输的比特数N有关。在多径RFC中的BER性能不仅与以上因素有关，还与信道的衰落系数有关。

3 系统仿真

本节主要针对HRNR-DCSK系统在AWGN信道及多径RFC进行仿真,主要从BSNREb/N0、所传输的比特数N以及扩频因子β的长度对系统BER性能的影响。仿真中采用的混沌序列是改进型的Logistic映射。在相同的扩频因子下,随着BSNR的变化,在不同传输比特下的BER性能曲线如图7所示。

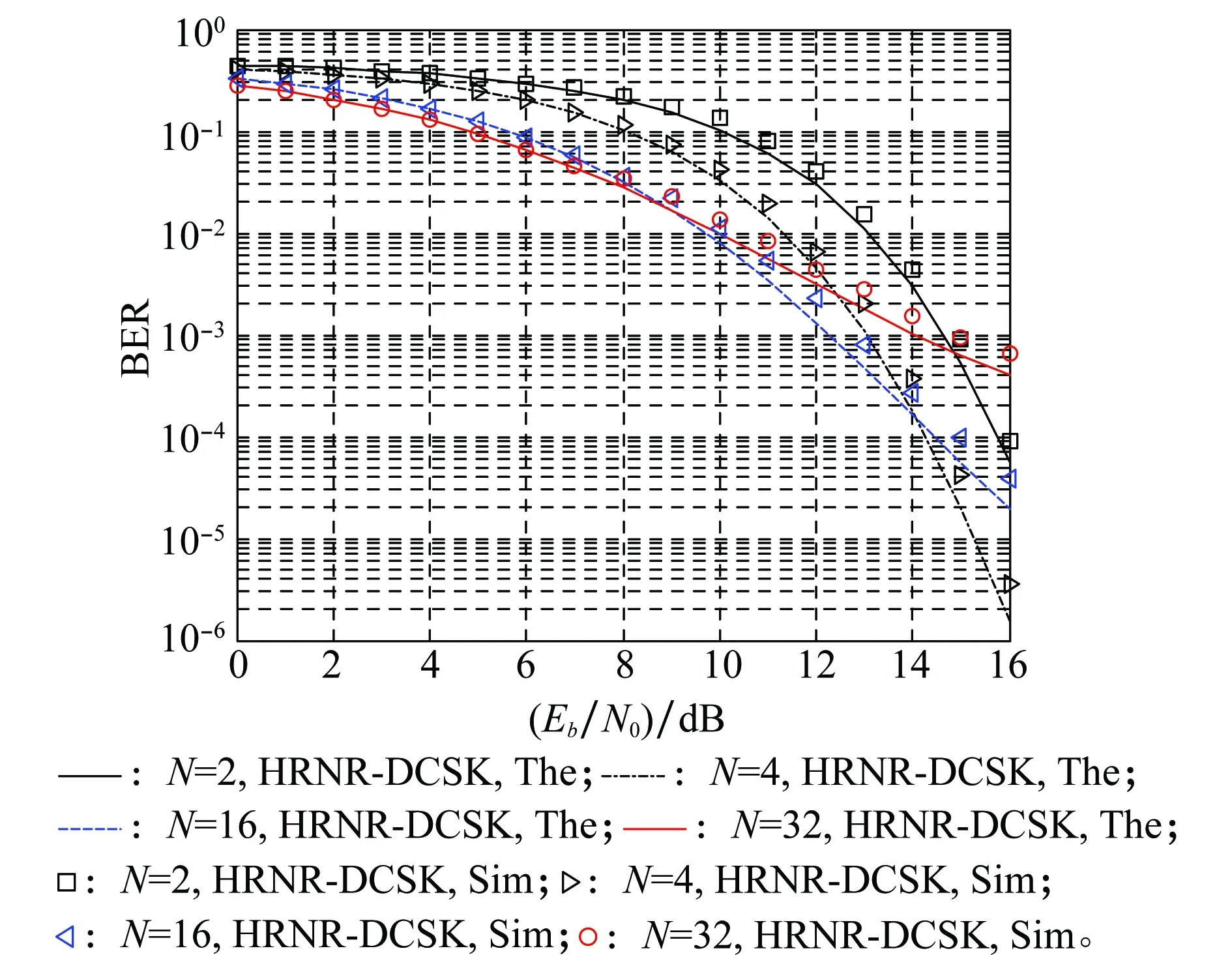
图7 β=256, N=2,4,16,32时HRNR-DCSK系统的性能BER曲线Fig.7 BER performance curves of HRNR-DCSK system for β=256 and N=2,4,16,32

通过图7可知，随着传输比特数目的增加,系统的BER性能会呈先上升后下降的趋势。一方面是随着传输比特数N的增加,平均比特能量Eb会逐渐降低,从而使得BER性能会逐渐得到提升。另一方面在传输比特数N逐渐增加到一定程度时,会得到更低的Eb但并不能使BER性能得到更好的提升。对其进一步说明:在Eb/N0较小时,N越大，Eb反而越小,此时的Eb对系统的BER性能曲线起主要作用,故使其保持在较低的水平;在Eb/N0较大时,在解调端虽使用移动平均滤波器来降低系统的噪声,但多次相关必定会增加码间串扰的可能,故Eb的降低并不能对BER性能的降低起到主导作用。在相同的扩频因子下,随着传输比特数的变化,在不同BSNR下的BER性能曲线如图8所示。

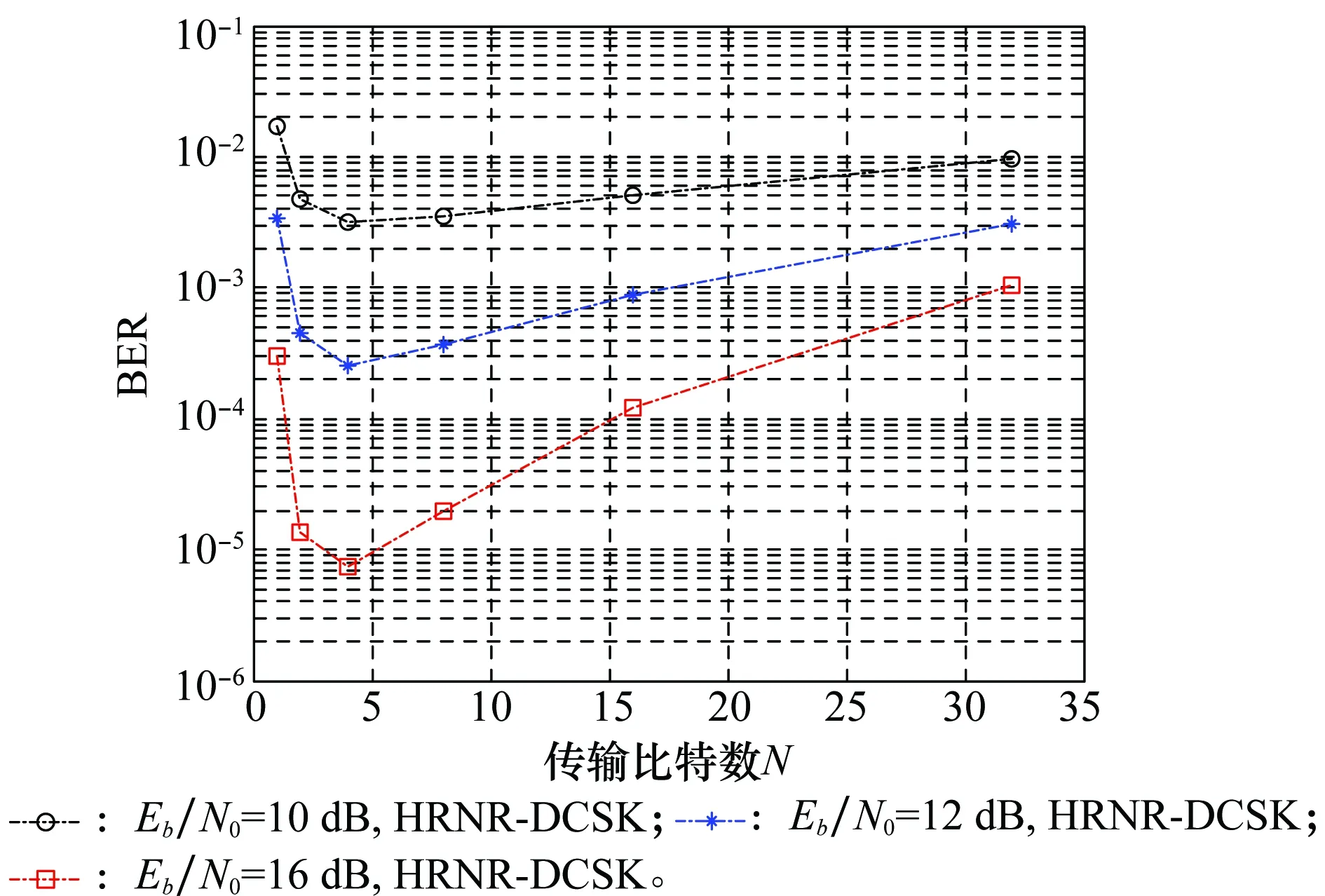
图8 β=256时HRNR-DCSK系统随传输比特数变化的系统BER性能曲线Fig.8 BER performances curves of HRNR-DCSK system with the number of transmission bits at β=256

通过图8可以看出,HRNR-DCSK系统的BER性能会随着传输比特数N的增加而呈现先下降后上升的趋势,在Eb/N0较小时,N=16时的性能优于N=2,4,但随着Eb/N0的增大,N=16的性能逐渐恶化,正好印证了图7的说明。由图8可以看出，在数据比特数N为4时,系统的BER性能最好,和图7呈现的结果一致。在相同的传输比特数下,随着扩频因子的变化,在不同BSNR下的BER性能曲线如图9所示。

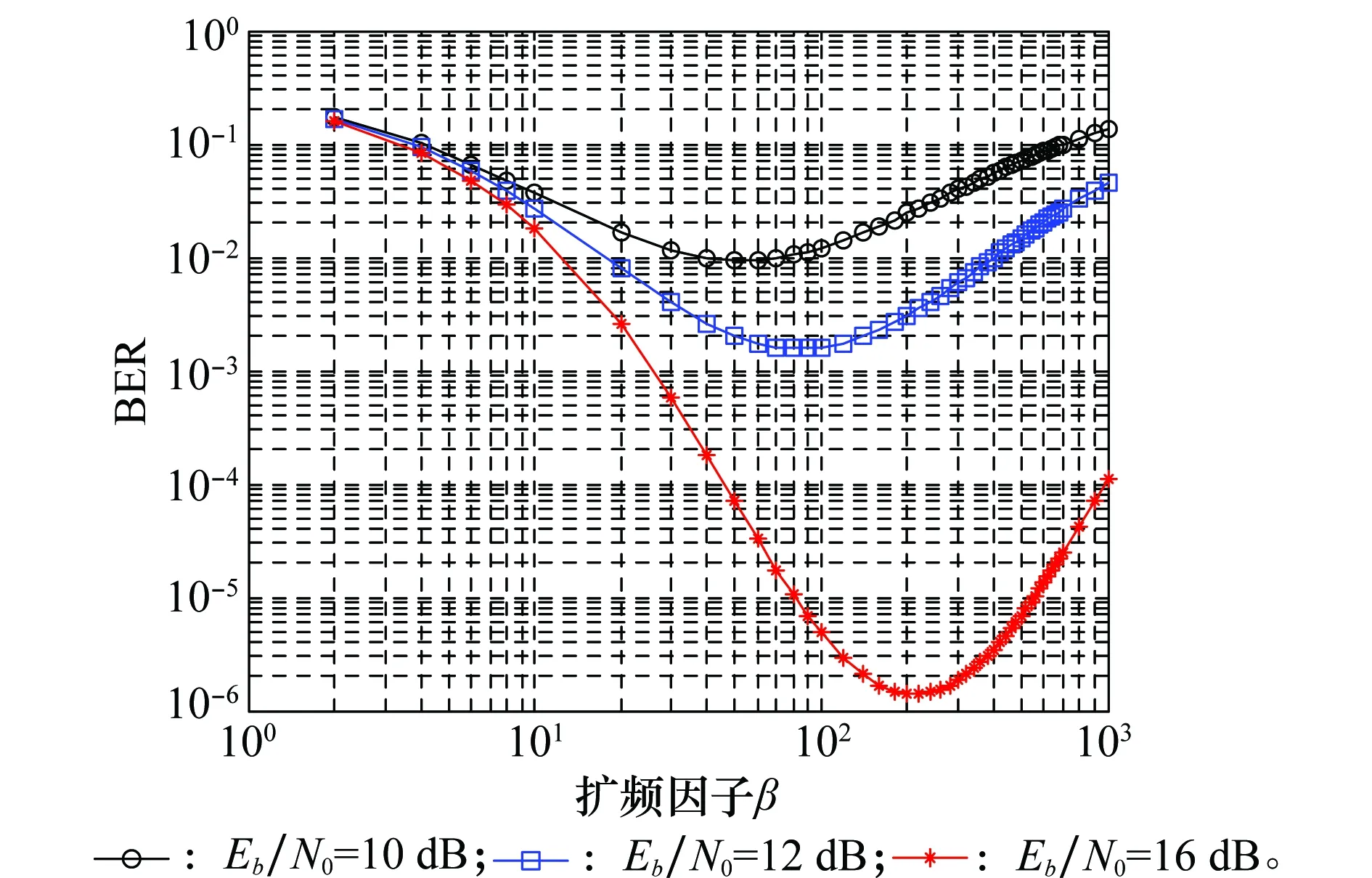
图9 N=4时HRNR-DCSK系统随扩频因子变化的BER性能曲线Fig.9 BER performances curves of HRNR-DCSK system with spread spectrum factor at N=4

通过图9可以看出,随着扩频因子β的变化,HRNR-DCSK系统的BER性能也是呈现先下降后上升的趋势,但是最佳的扩频序列长度是随着BSNREb/N0的增大而增大。在扩频因子与比特数比值一定的情况下,随着BSNR的变化,在不同比特数下的BER性能曲线如图10所示。

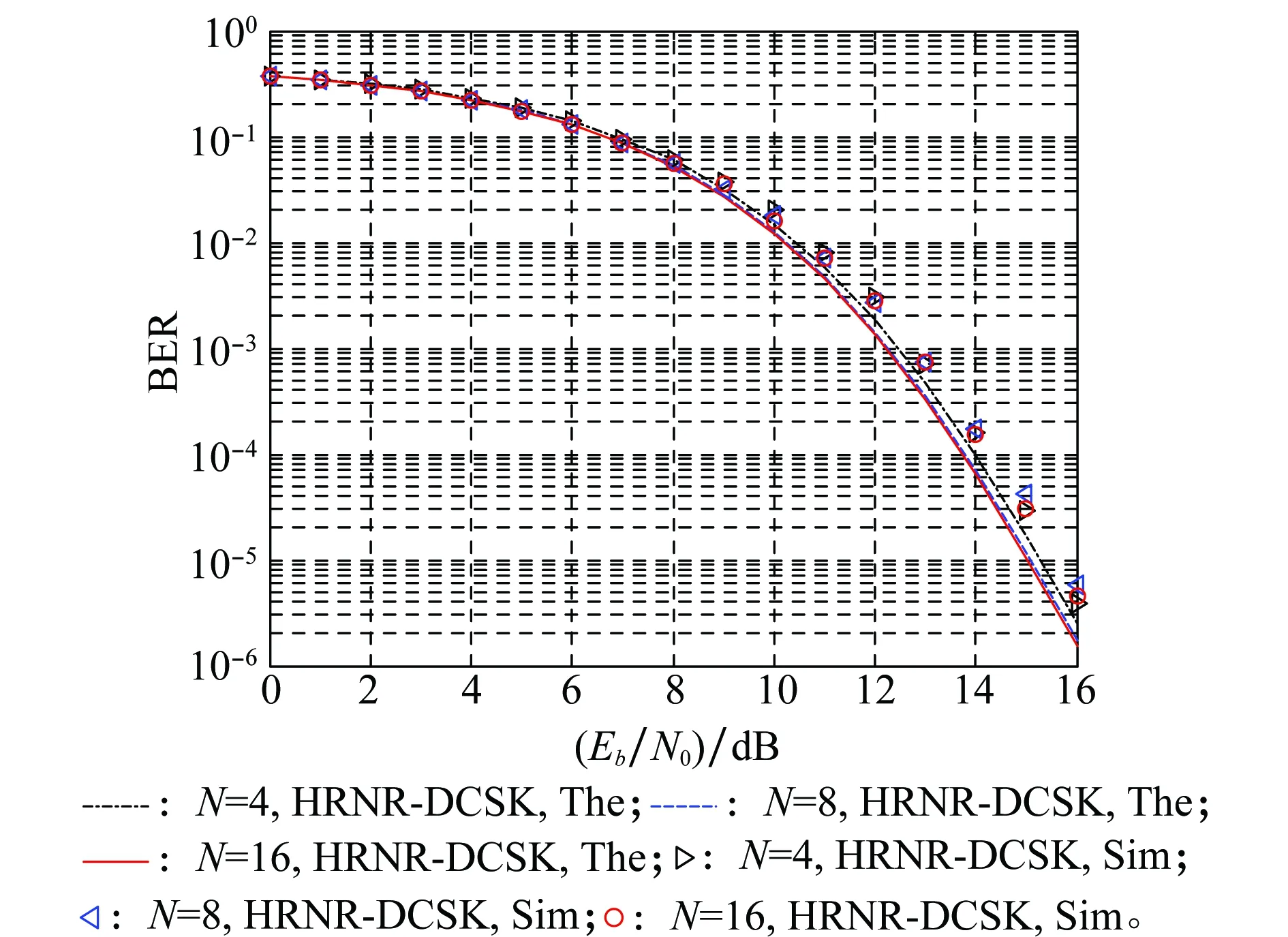
图10 β/N=32时HRNR-DCSK系统的BER性能曲线Fig.10 BER performance curves of HRNR-DCSK system for β/N=32 in AWGN channels

由图10可知,在β/N为相同值时,HRNR-DCSK系统的BER性能几乎一致。说明Eb对系统BER性能的降低的程度和码间串扰对BER性能的提高的程度几乎相同。HRNR-DCSK系统与DCSK、SR-DCSK[18]、NR-DCSK[19]、HE-DCSK系统对比的BER曲线如图11所示。

图11 β=128时不同系统的BER性能曲线Fig.11 BER performance curves of different systems for β=128

对于仿真条件是在β=256,N=2,P=2下进行的,从图中可以看出，在相同的扩频因子下,HRNR-DCSK表现出较好的BER性能。HRNR-DCSK系统在多径RFC不同情况下的BER性能曲线如图12和图13所示。分别是通过以下几个情况进行仿真。

情况1第1个信道的平均信道增益和第2个信道的平均信道增益相等,即

情况2第1个信道的平均信道增益比第2个信道的平均信道增益高6 dB,即

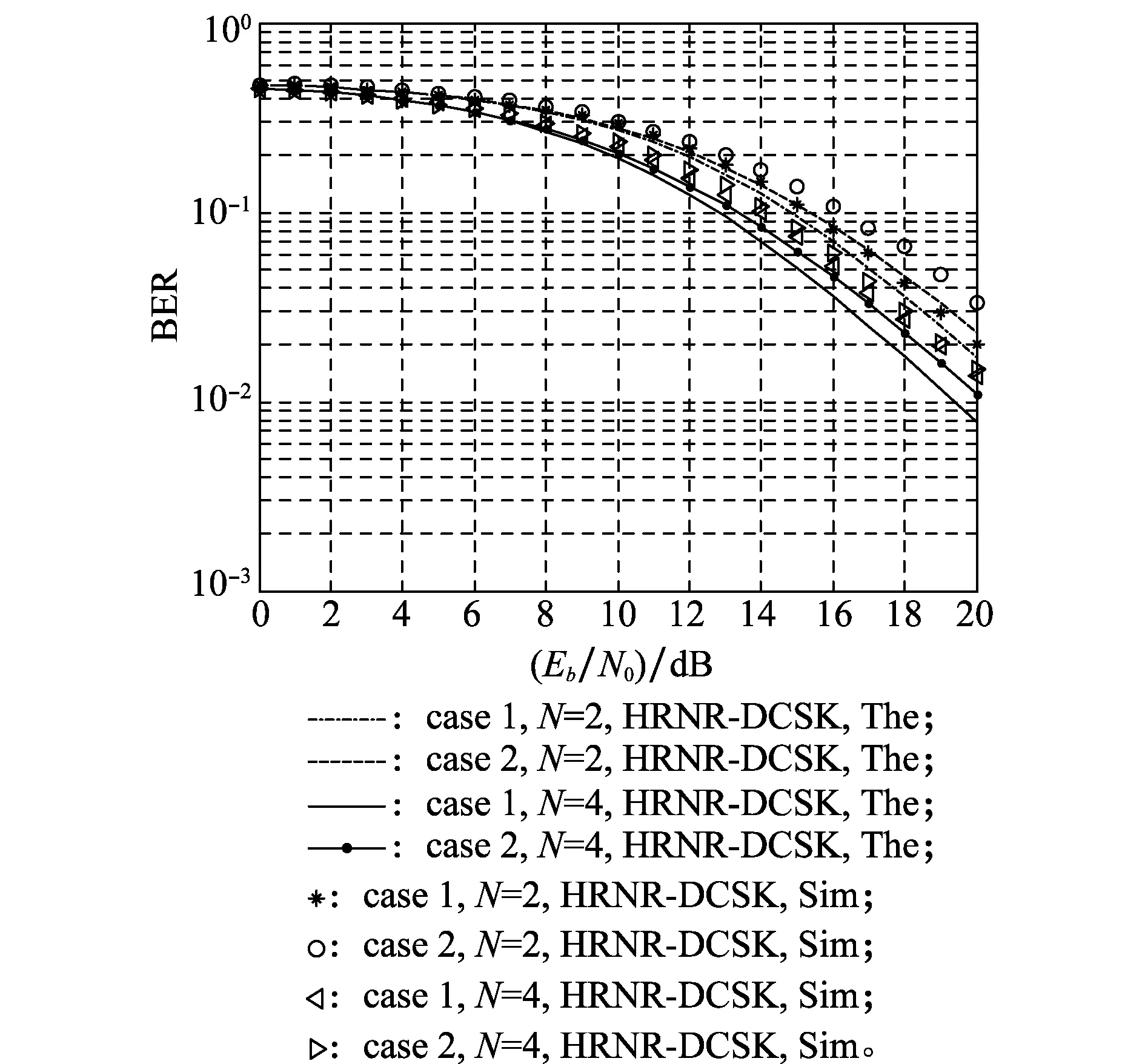
图12 当β=1 024时HRNR-DCSK系统的BER性能曲线Fig.12 BER performance curves of HRNR-DCSK for β=1 024 in Rayleigh fading channel

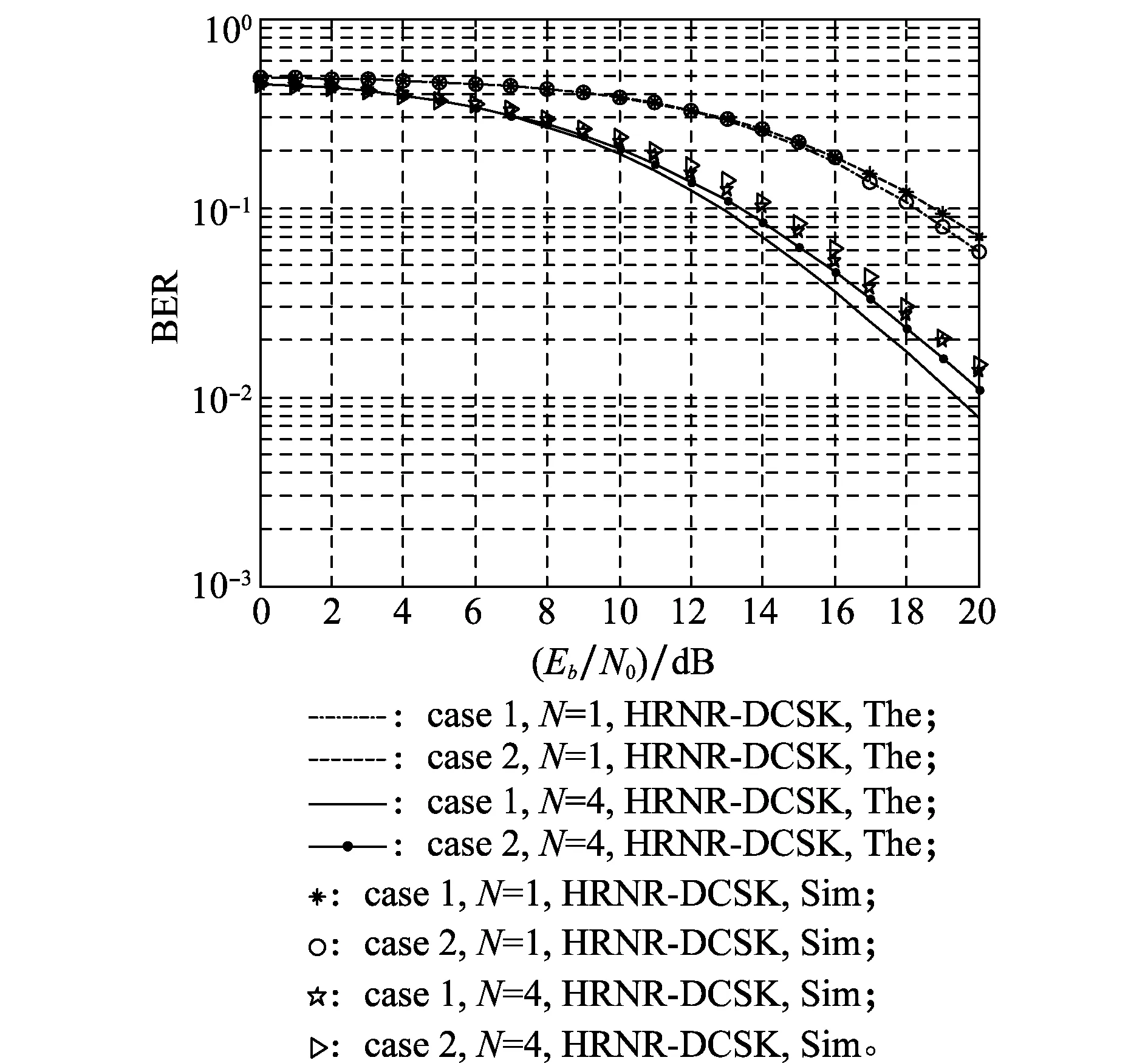
图13 当β=1 024时HRNR-DCSK系统的BER性能曲线Fig.13 BER performance of HRNR-DCSK for β=1 024 in Rayleigh fading channel

从图12和图13可以看出,在同一情况下较大的数据传输比特比较小时呈现出更好的BER性能,说明在扩频因子β较大时,Eb的降低对BER性能的下降起到主导作用。在图13中,当N=1时呈现的是传统的DCSK系统,通过对比发现,在扩频因子β较大时,HRNR-DCSK系统比传统的DCSK系统拥有更好的BER性能。这是由于N的增大使得比特能量Eb的降低,对系统的BER性能起到主要作用。

4 结 论

本文提出了一种新型的非相干混沌通信系统——HRNR-DCSK系统。该系统降低了原有DCSK系统的参考信号的长度,将原有的数据信号扩展为多个时隙,每个时隙传输不同的数据比特,同时在接收端通过降低噪声方差的方式进行接收并解调。在文中对该系统通过GA法推导了在AWGN信道和多径RFC下的公式,并对其进行了蒙特卡罗仿真。该系统的参考信号长度及比特能量会随着传输比特的增加而降低,从而相较于传统DCSK系统提高了数据传输速率,降低了每比特发射功率。在推导中发现系统的BER性能主要与数据传输比特数N、扩频因子β及BSNREb/N0有关,并通过仿真分析了每个变量对系统BER性能的影响。在仿真中发现在参考时隙长度相同时，不同的传输比特数之间具有几乎相同的BER性能。在多径RFC的仿真中发现:当不同路径间信道增益相同和不同时都表现出了N越大抗信道衰落的能力越强。

在发射端使用改进型的正交混沌信号,在接收端对接收的信号进行移动平均滤波,这样的操作提高了系统的复杂度,在某种程度上降低了系统的安全性,但为了提高数据传输速率,降低每比特发射功率,提高系统的BER性能,这样的牺牲是值得的。

参考文献：

[1] DUAN J Y, JIANG G P, YANG H. Reference-adaptive CDSK: an enhanced version of correlation delay shift keying[J]. IEEE Trans.on Circuits and System-II: Express Briefs, 2015, 62(1): 90-94.

[2] 赵雅琴,李书营,米雪龙,等.基于STBC技术的DCSK通信系统性能分析[J].系统工程与电子技术,2016,38(1):155-162.

ZHAO Y Q, LI S Y, MI X L, et al. Performance analyze for STBC-based DCSK communication system[J].Systems Engineering and Electronics,2016, 38(1): 155-162.

[3] 张刚, 王传刚, 张天骐. 基于正交混沌载波的多用户DCSK系统性能分析[J]. 系统工程与电子技术, 2017, 39(2): 431-436.

ZHANG G, WANG C G, ZHANG T Q. Performance analyze for MU-DCSK system based on orthogonal chaotic carrier[J]. Systems Engineering and Electronics, 2017, 39(2): 431-436.

[4] KADDOUM G, TRAN H V, LONG K, et al. Design of simultaneous wireless information and power transfer scheme for short reference DCSK communication systems[J]. IEEE Trans.on Communications, 2017,65(1): 431-443.

[5] DEDIEU H, KENNEDY M P, HASLER M. Chaos shift keying: modulation and demodulation of a chaotic carrier using self-synchronizing Chua’s circuits[J]. IEEE Trans.on Circuits & Systems II Analog & Digital Signal Processing, 1993, 40(10): 634-642.

[7] HERCEG M, MILICEVIC K, MATIC T. Correlation-multi-delay-shift-keying for chaos based communications[J]. Wireless Personal Communications, 2015, 88(2):1-12.

[8] GALIAS Z, MAGGIO G M. Quadrature chaos-shift keying: theory and performance analysis[J]. IEEE Trans.on Circuits & Systems I Fundamental Theory & Applications, 2002, 48(12):1510-1519.

[9] KADDOUM G, SOUJERI E, ARCILA C, et al. I-DCSK: an improved noncoherent communication system architecture[J]. IEEE Trans.on Circuits & Systems II Express Briefs,2015,62(9): 901-905.

[10] CAI G, WANG L, HUANG T. Channel capacity of M-ary differential chaos shift keying modulation over AWGN channel[C]∥Proc.of the International Symposium on Communications and Information Technologies, 2013:91-95.

[11] CHEN P, WANG L, CHEN G. DDCSK-Walsh coding: a reliable chaotic modulation-based transmission technique[J]. IEEE Trans.on Circuits & Systems II Express Briefs, 2012, 59(2):128-132.

[12] KADDOUM G, GAGNON F, RICHARDSON F D. Design of a secure multi-carrier DCSK system[C]∥Proc.of the International Symposium on Wireless Communication Systems, 2012:964-968.

[13] KADDOUM G, RICHARDSON F D, GAGNON F. Design and analysis of a multi-carrier differential chaos shift keying communication system[J]. IEEE Trans.on Communications, 2013, 61(8):3281-3291.

[14] XU W K, WANG L. A novel differential chaos shift keying modulation scheme[J]. International Journal of Bifurcation & Chaos, 2011, 21(3):799-814.

[15] KADDOUM G, GAGNON F. Design of a high-data-rate differential chaos-shift keying system[J]. IEEE Trans.on Circuits & Systems II Express Briefs, 2012, 59(7):448-452.

[16] YANG H, JIANG G P. High-efficiency differential-chaos-shift-keying scheme for chaos-based noncoherent communication[J]. IEEE Trans.on Circuits & Systems II Express Briefs, 2012, 59(5):312-316.

[17] YANG H, JIANG G P. Reference-modulated DCSK: a novel chaotic communication scheme[J]. IEEE Trans.on Circuits & Systems II Express Briefs, 2013, 60(4):232-236.

[18] KADDOUM G, SOUJERI E, NIJSURE Y. Design of a short reference noncoherent chaos-based communication systems[J]. IEEE Trans.on Communications, 2016, 64(2):680-689.

[19] KADDOUM G, SOUJERI E. NR-DCSK: a noise reduction differential chaos shift keying system[J]. IEEE Trans.on Circuits & Systems II Express Briefs, 2016, 63(7):648-652.