融合记分函数的直觉模糊集相似度性质再定义与模型设计
江文奇, 祁晨晨, 王晨晨
(南京理工大学经济管理学院江苏产业集群决策咨询研究基地, 江苏 南京 210094)
0 引 言
1986年,文献[1]拓展了模糊集理论,运用隶属度、非隶属度和犹豫度来全面表征评估者的判断,更加符合现实情形,已在聚类分析、模式识别、医疗诊断等领域得到广泛应用。在多准则决策问题中,直觉模糊集(intuitionistic fuzzy sets,IFS)的相似度是决策的重要因素之一,对决策结果产生重要影响,如何设计IFS的相似度成为重要的研究问题。
较为经典的IFS的相似度度量主要采用距离测度模型。如文献[2-3]早期提出了相似度度量距离模型;文献[4]分析了两个模型的缺点并进行了改进;文献[5]运用欧式距离进行度量;文献[6]给出了IFS相似度的定义,并将模糊集的相似度量方法推广到IFS;文献[7] 指出文献[6]中相似度的应用局限性,并提出新的相似度;文献[8]基于Hausdorff距离构建直觉模糊相似度;文献[9]则构建了含有犹豫度的相似度模型;文献[10]分析了上述相似度不符合直觉思维问题,基于Lp度量提出新的相似度;文献[11]针对相似度的距离度量可能导致反直觉的情形,提出了基于层次的相似度度量方法。为了降低距离测量中的信息损失,文献[12-13]将IFS转化为直角三角形的重心和三角模糊数,提出相似性度量模型;文献[14]进一步基于转换的直角三角模糊数的中心点来测量相似度。
为了规避距离测度可能造成的识别和比较困难问题,文献[15]从集合论的观点出发构建直觉模糊相似度;文献[16]提出了余弦相似度测量方法;文献[17]则提出了基于余弦相似度和欧几里德距离的相似性度量模型;文献[18]提出基于Frank t-范数族的直觉模糊相似性度量;文献[19]考虑了犹豫度因素,提出了运用相关系数表示相似度;文献[20]利用模糊蕴含算子和集合基数提出基于包含度的相似性度量方法;文献[21]综合考虑了隶属度、非隶属度、犹豫度和直觉指数对隶属度函数的影响,提高了匹配精度;文献[22]基于Sugeno积分提出新的相似度;文献[23]基于匹配函数提出新的相似性度量方法;为了识别不确定性,文献[24]提出了新的IFS之间相似性度量的公理化定义,并从相似性和犹豫性2个方面构造二元组相似性度量;文献[25]为较好区分IFS而提出新的相似度模型;文献[26]则基于限制IFS隶属度的区间端点凸组合来定义相似度;文献[27]提出了基于知识测度的相似性度量方法来评估IFS和互补集之间最相似和最不相似的情况;文献[28]提出基于激活检测的相似性度量方法;文献[29]基于隶属度函数、非隶属度函数、犹豫度函数和隶属度函数的上界定义相似度;文献[30]提出了基于邻域的相似度构建方法,并应用于图像处理领域;文献[31]基于最大最小算子提出直觉模糊相似性度量。
在考虑权重的情形下,文献[32]提出了基于距离测度的加权相似度测量方法;文献[33]利用聚合函数整合现有的距离测量并赋予权重;文献[34]认为相似度越低权重越低,并提出直觉模糊有序加权余弦相似性度量;文献[35]针对现实世界中元素间一般相互关联的问题,提出用Shapley加权相似度来处理这种特性间的交互作用;文献[36]提出了用IFS表示的加权相似度,可以降低信息损失,更能反映IFS的特性。
上述研究文献分别从不同角度提出了相似度度量模型,有利于实现直觉模糊型多准则决策。然而,部分文献提出的相似度模型并不符合相似度的具体特征或者没有考虑一般情形下的相似度特征,导致相似度结果无法真正体现其具体特征。于是,本文首先考虑了一般情形下IFS的相似度的具体特征,分析现有相似度函数与该特征的匹配度,进而提出一种新的IFS相似度测量方法,最后通过算例分析和灵敏度分析来阐明本方法的优越性和应用价值。
1 预备知识
定义1[1]设X是一个给定论域,则X上的一个IFS为A={〈x,μA(x),vA(x)〉|x∈X}。其中μA(x)和vA(x)分别为X中元素x属于A的隶属度和非隶属度,μA:X→[0,1],vA:X→[0,1],且满足条件0≤μA(x)+vA(x)≤1,x∈X。称πA(x)=1-μA(x)-vA(x)为X中元素x属于A的犹豫度。
定义2[1]设A和B是给定论域X上的IFS,则有:
(1) IFS相等关系:A=B当且仅当对任意x∈X,有μA(x)=μB(x),vA(x)=vB(x)。
(2) IFS包含关系:A⊆B当且仅当对任意x∈X,有μA(x)≤μB(x),vA(x)≥vB(x)。
(3) IFS的交:A∩B= {〈x,min(μA(x),μB(x)),max(vA(x),vB(x))|∀x∈X〉}。
(4) IFS的并:A∪B= {〈x,max(μA(x),μB(x)),min(vA(x),vB(x))|∀x∈X〉},文献[6]首先定义了IFS的相似度(条件1~条件3、条件5),文献[20]在此基础上完善了相似度性质,添加了条件4。IFS相似度定义如下:
定义3[6]设S是一个映射,且S:IFS(X)×IFS(X)→[0,1]。称S(A,B)为IFSA∈IFS(X)和B∈IFS(X)间的相似度,S(A,B)满足以下条件:
条件10≤S(A,B)≤1;
条件2S(A,B)=1,当且仅当A=B;
条件3S(A,B)=S(B,A);
条件4S(A,B)=0,当且仅当A=〈0,1〉,B=〈1,0〉或A=〈1,0〉,B=〈0,1〉;
条件5如果A⊆B⊆C,则S(A,C)≤S(A,B),S(A,C)≤S(B,C)。
定义4[37-38]设A=〈μA(x),vA(x)〉,B=〈μB(x),vB(x)〉是2个IFS,则MA(x)和MB(x)分别是A和B的记分函数;HA(x)和HB(x)分别是A和B的精确函数。其中MA(x)=μA(x)-vA(x),MB(x)=μB(x)-vB(x);HA(x)=μA(x)+vA(x),HB(x)=μB(x)+vB(x)。则2个IFSA和B的比较为:
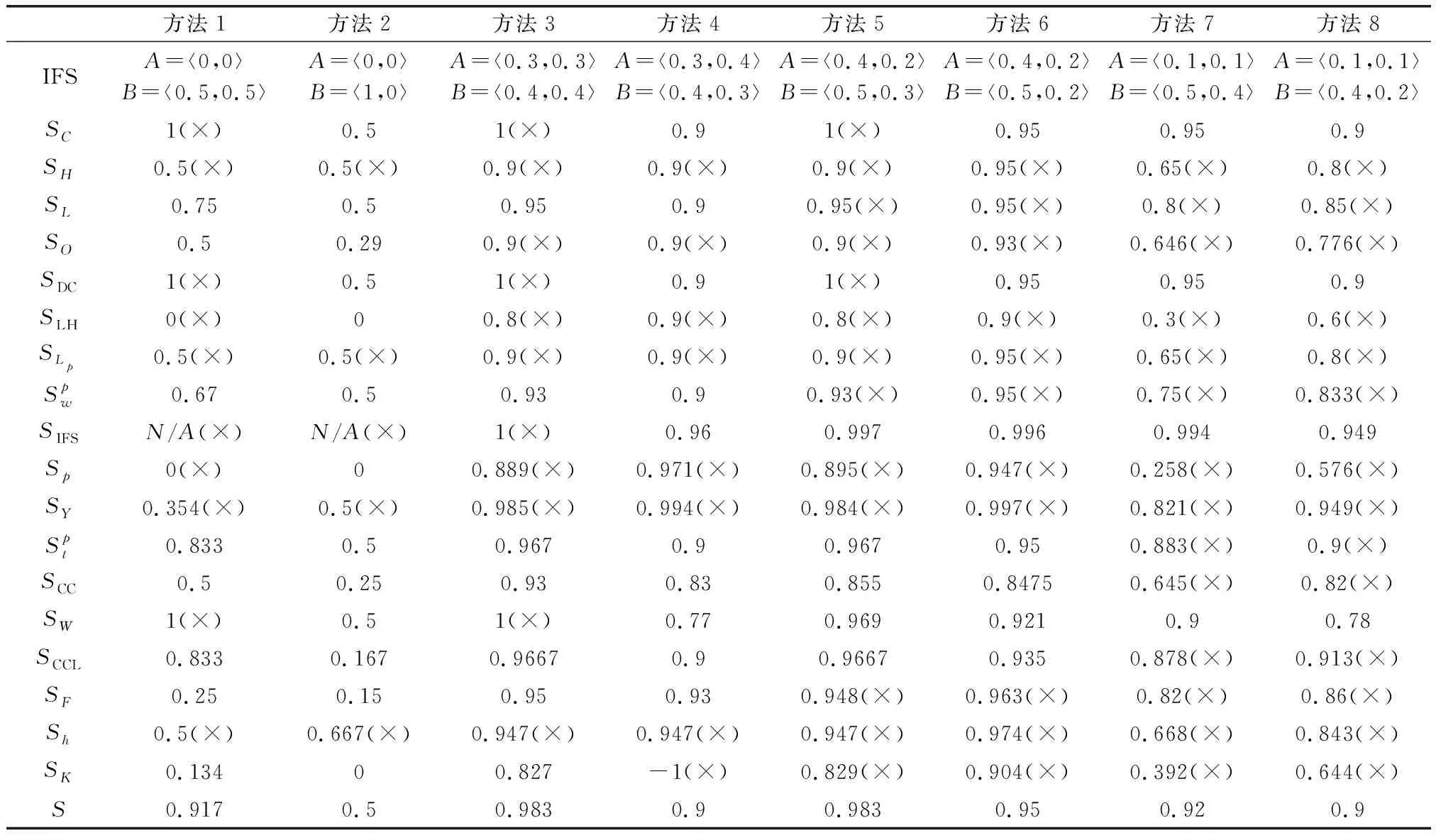
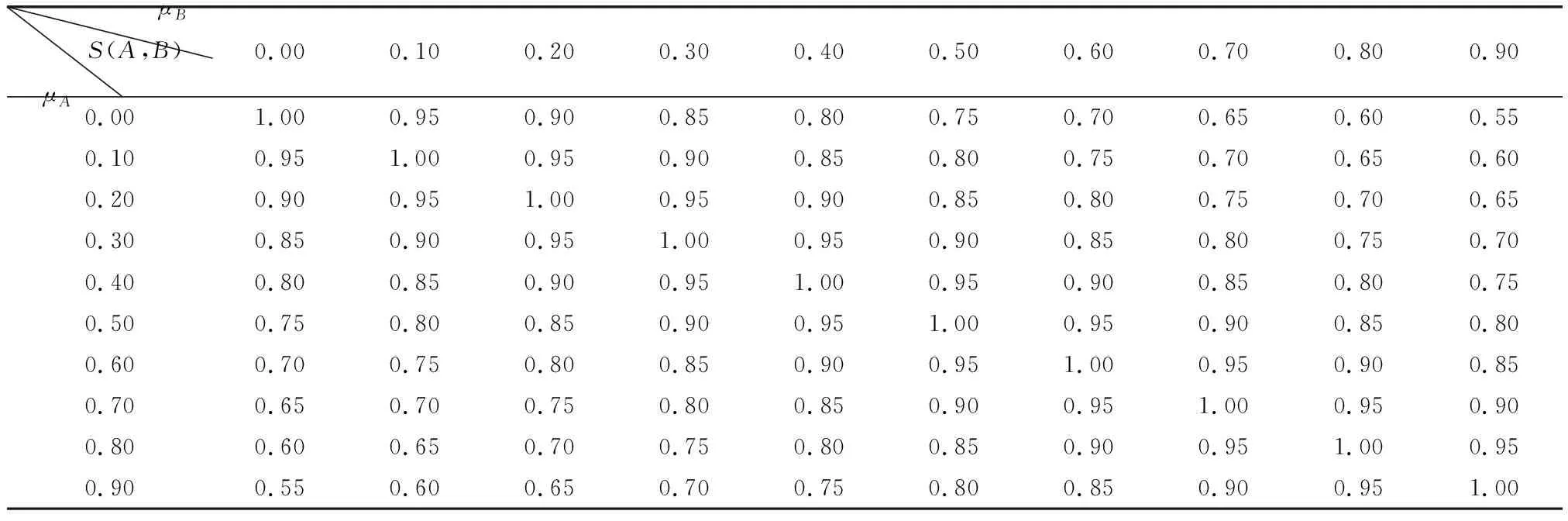
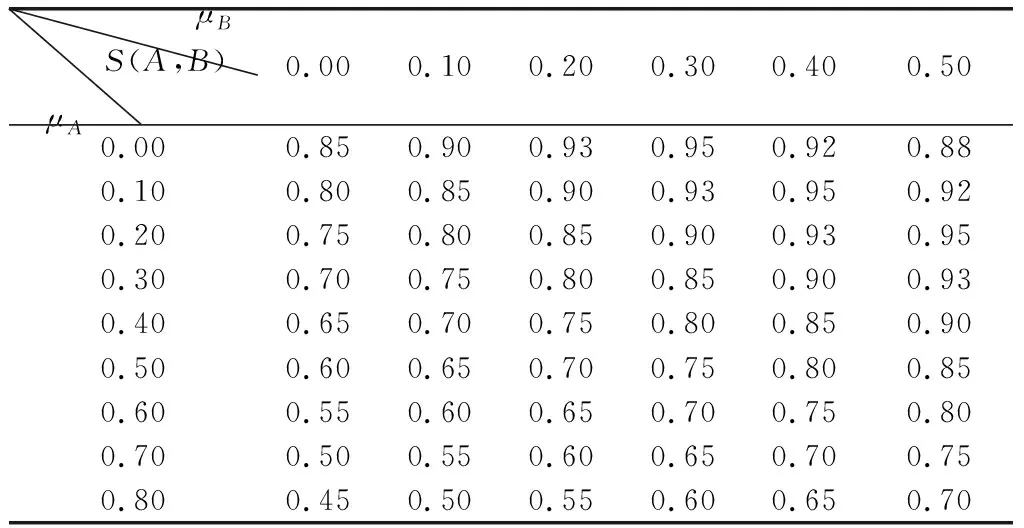
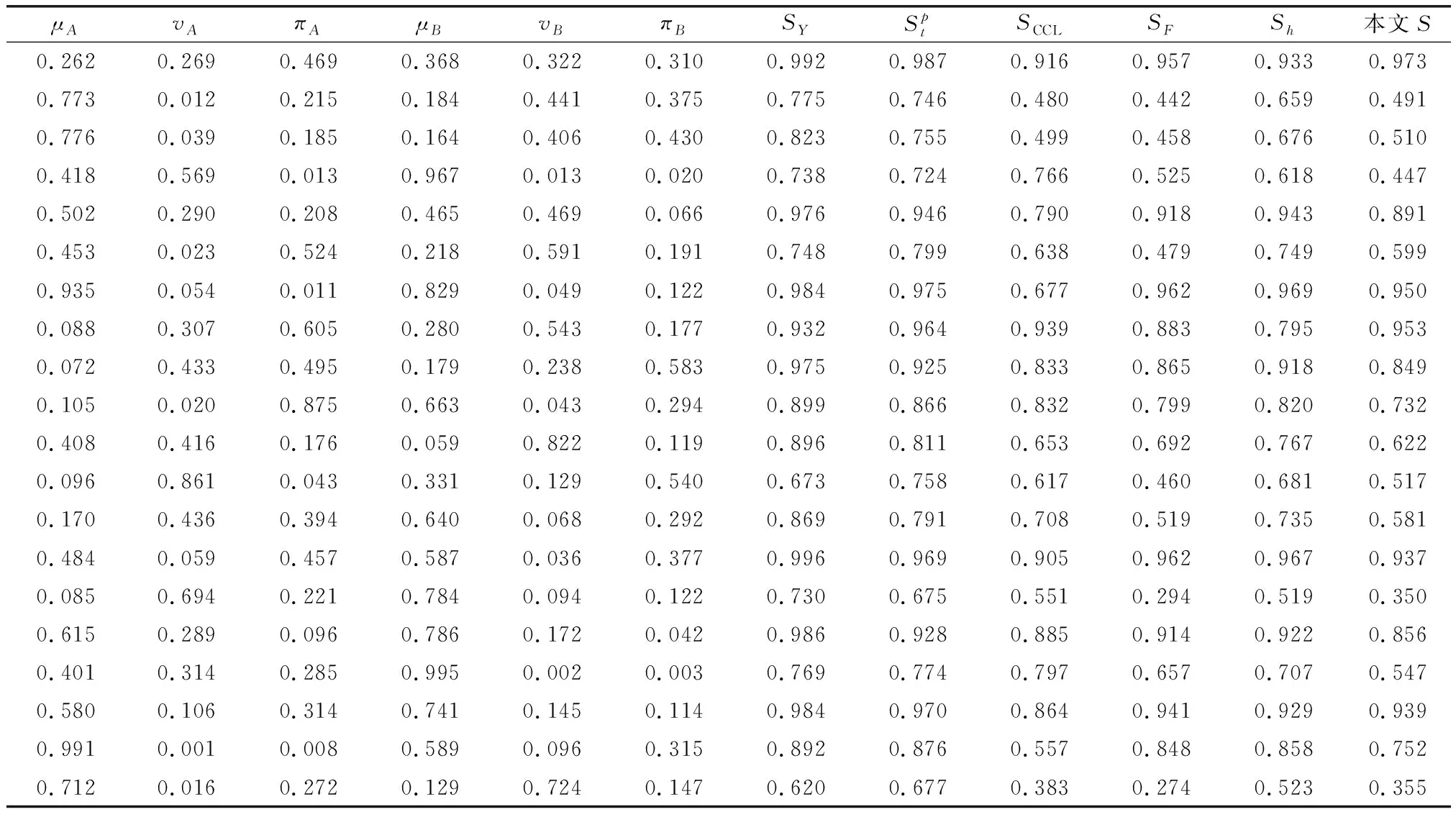
(1)若MA(x) (2)若MA(x)>MB(x),则A>B; (3)若MA(x)=MB(x),则 ①HA(x) ②HA(x)>HB(x)时,A>B。 为了简便起见,若IFSA={〈x,μA(x),vA(x)〉|x∈X}只有一个元素,常将A简写为A=〈μA(x),vA(x)〉。以下记μA表示μA(x),μB表示μB(x),vA表示vA(x),vB表示vB(x)。则现有IFS相似度函数的度量方法列举如下: (1)文献[2]定义相似度为 (1) (2)文献[3]定义相似度为 (2) (3)文献[4]在文献[2-3]的基础上提出新的相似度公式,即 |(μA-μB)|+|(vA-vB)|] (3) (4)文献[5]基于欧几里德距离提出新的相似度,即 (4) (5)文献[6]给出了相似度的公理化定义,并提出了新的相似度,即 (5) (6)文献[9]考虑了犹豫度,定义相似度为 SLH(A,B)= (6) 式中,p≥1。 (7) 文献[10]基于Lp度量提出新的相似度,即 (7) (8) 文献[32]基于距离测度提出新的相似度,即 (8) (9) 文献[16]提出余弦相似度,即 (9) (10) 文献[23]基于匹配函数提出新的相似度,即 (10) (11) 文献[25]提出新的相似度,即 SY(A,B)= (11) (12)文献[12]提出基于双参数的相似度度量方法,即 (12) 式中,t=2,3,4,…;p=1,2,3,…。 (13)文献[13]基于转换的三角模糊数提出相似度度量模型,即 (13) 式中,Axi是转换的三角模糊数,即Axi=(μA,μA,1-vA)。 (14) 文献[20]为了降低信息损失且提高区分度,提出基于倾向性的相似度量方法,即 (14) (15) 文献[14]提出基于转换的直角三角模糊数的中心点来测量IFSs之间相似度,即 (15) (16) 文献[13]提出基于余弦相似度和欧几里德距离的相似度,即 (16) (17) 文献[11]为提高分类准确度,给出新的相似度,即 Sh(A,B)= (17) (18) 文献[27]基于知识测度提出相似度测量方法,即 SK(A,B)= (18) 针对定义3中的条件5,要满足A⊆B⊆C则μA≤μB≤μC,vA≥vB≥vC,这种假设在现实中很难成立。很多IFS并不满足上述强假设,而记分函数可以表征一般情形下IFS的顺序,扩展条件5,即: 条件6如果MA≤MB≤MC,则:S(A,C)≤S(A,B),S(A,C)≤S(B,C); 条件7如果MA=MB=MC,HA≤HB≤HC时,则S(A,C)≤S(A,B),S(A,C)≤S(B,C)。 基于扩展的定义3的7个条件,现有的相似度存在一些缺陷,主要表现在: (1)SC,SDC,SIFS,SW不满足条件2。例如:A=〈0.3,0.3〉,B=〈0.4,0.4〉时,显然A≠B,但SC(A,B)=SDC(A,B)=SIFS(A,B)=SW(A,B)=1。当μA=vA=0或者μB=vB=0时,分母为0,则SIFS值不存在,如A=〈0.5,0.5〉,B=〈0,0〉。SC与SDC不满足条件7,如A=〈0.3,0.2〉,B=〈0.4,0.3〉,C=〈0.5,0.4〉时,S(A,B)=S(A,C)=S(B,C)=1。 (2)SLH不满足条件4。如A=〈0.5,0.5〉,B=〈0,0〉,C=〈1,0〉时,可以得SLH(A,B)=SLH(B,C)=0不成立。同例,对于Sp和SK条件也不成立。 (3)SK不满足条件1和条件5。如果A=〈0.3,0.4〉,B=〈0.4,0.3〉得SK(A,B)=-1<0;如果A=〈0.3,0.3〉,B=〈0.3,0.2〉,C=〈0.4,0.2〉,此时A⊆B⊆C,应有S(A,C)≤S(B,C),然而SK(A,C)=0.99>SK(B,C)=0.907。Sp也不满足条件5,如A=〈0.3,0.3〉,B=〈0.3,0.2〉,C=〈0.4,0.2〉,得Sp(A,B)=0.92 于是,比较上述相似度函数与本文定义的7个条件的匹配程度,如表1所示。 表1 现有文献约束条件满足情况 由表1可知,上述相似度函数不完全满足定义3的条件及本文增加的2个条件,因此有必要重新设计新的相似度函数且其必须完全满足7个条件。 设A=〈μA,vA〉,B=〈μB,vB〉是2个IFS,定义A与B之间的相似度为 S(A,B)=1-[|(μA-vA)-(μB-vB)|+ |(2μA-vA)-(2μB-vB)|/3+ |(2vA-μA)-(2vB-μB)|/3]/4 (19) 定理1式(19)定义的S(A,B)是一个直觉模糊相似度,满足条件1~条件7。 证明(1)针对条件1,因为 -1≤μA-vA≤1,-1≤μB-vB≤1⟹ 0≤|(μA-vA)-(μB-vB)|≤2; 由于 -1≤2μA-vA≤2,-1≤2μB-vB≤2⟹ 0≤|(2μA-vA)-(2μB-vB)|/3≤1; 同理,0≤|(2vA-μA)-(2vB-μB)|/3≤1。 所以 |(μA-vA)-(μB-vB)|+|(2μA-vA)-(2μB-vB)|/3+ |(2vA-μA)-(2vB-μB)|/3≤4⟹S(A,B)≥0 因此,0≤S(A,B)≤1。 (2)条件2显然成立。 (3)针对条件3,如果S(A,B)=1,则 |(μA-vA)-(μB-vB)|+|(2μA-vA)-(2μB-vB)|/3+ |(2vA-μA)-(2vB-μB)|/3=0 于是 μA-vA=μB-vB,2μA-vA=2μB-vB, 2vA-μA=2vB-μB, 所以,μA=μB,vA=vB⟺A=B。 (4) 针对条件4,如果S(A,B)=1,则|(μA-vA)-(μB-vB)|+|(2μA-vA)-(2μB-vB)|/3+|(2vA-μA)-(2vB-μB)|/3=4,有:|(μA-vA)-(μB-vB)|=2,|(2μA-vA)-(2μB-vB)|=3,|(2vA-μA)-(2vB-μB)|=3,|(μA-μB)-(vA-vB)|=2,|2(μA-μB)-(vA-vB)|=3,|(μA-μB)-2(vA-vB)|=3,⟺μA-μB=1,vA-vB=-1或者μA-μB=-1,vA-vB=1,因此,A=〈1,0〉,B=〈0,1〉或者A=〈0,1〉,B=〈1,0〉。 (5)针对条件5,如果A⊆B⊆C有μA≤μB≤μC,vA≥vB≥vC,可得:μA-vA≤μB-vB≤μC-vC,于是:2μA-vA≤2μB-vB≤2μC-vC, 2vA-μA≥2vB-μB≥2vC-μC,令 12D(A,B)=3|(μA-vA)-(μB-vB)|+ |(2μA-vA)-(2μB-vB)|+|(2vA-μA)-(2vB-μB)|= 3(μB-vB)-3(μA-vA)+(2μB-vB)- (2μA-vA)+(2vA-μA)-(2vB-μB) 12D(A,C)=3|(μA-vA)-(μC-vC)|+ |(2μA-vA)-(2μC-vC)|+|(2vA-μA)-(2vC-μC)|= 3(μC-vC)-3(μA-vA)+(2μC-vC)-(2μA-vA)+ (2vA-μA)-(2vC-μC) 于是 12(D(A,B)-D(A,C))= [3(μB-vB)-3(μC-vC)]+[(2μB-vB)-(2μC-vC)]+ [(2vC-μC)-(2vB-μB)]≤0⟹ D(A,B)≤D(A,C)⟹S(A,C)≤S(A,B) 同理,S(A,C)≤S(B,C)。 (6) 针对条件6,如果MA≤MB≤MC,则有S(A,C)≤S(A,B),S(A,C)≤S(B,C)。因为MA≤MB≤MC,即μA-vA≤μB-vB≤μC-vC。于是 4D(A,B)=(μB-vB)-(μA-vA)+ |(2μA-vA)-(2μB-vB)|/3+ |(2vA-μA)-(2vB-μB)|/3 4D(A,C)=(μC-vC)-(μA-vA)+ |(2μA-vA)-(2μC-vC)|/3+ |(2vA-μA)-(2vC-μC)|/3 如果 (2μA-vA)-(2μB-vB)<0, (2vA-μA)-(2vB-μB)>0, (2μA-vA)-(2μC-vC)<0, (2vA-μA)-(2vC-μC)>0 因此 4D(A,B)=(μB-vB)-(μA-vA)+ [(2μB-vB)-(2μA-vA)]/3+ [(2vA-μA)-(2vB-μB)]/3 4D(A,C)=(μC-vC)-(μA-vA)+ [(2μC-vC)-(2μA-vA)]/3+ [(2vA-μA)-(2vC-μC)]/3 则 4(D(A,B)-D(A,C))= (μB-vB)-(μC-vC)+ [(2μB-vB)-(2μC-vC)]/3+ [(2vC-μC)-(2vB-μB)]/3= 2((μB-vB)-(μC-vC))≤0⟹ D(A,B)≤D(A,C)⟹S(A,C)≤S(A,B) 同理,S(A,C)≤S(B,C)。 如果 (2μA-vA)-(2μB-vB)<0, (2vA-μA)-(2vB-μB)<0, (2μA-vA)-(2μC-vC)<0, (2vA-μA)-(2vC-μC)>0 因此 4(D(A,B)-D(A,C))= (μB-vB)-(μC-vC)+[(2μB-vB)-(2μC-vC)]/3+ [(2vB-μB)-2(2vA-μA)-(2vC-μC)]/3= 2(2μB-vB-3μC+3vC+μA-2vA)/3≤ 2(2μB-vB-3μC+3vC+μB-2vB)/3= 2((μB-vB)-(μC-vC))≤0 得到:D(A,B)≤D(A,C)⟹S(A,C)≤S(A,B)。同理,S(A,C)≤S(B,C)。 其他几种情形仍然可以证明。 (7)针对条件7,如果MA=MB=MC,HA≤HB≤HC,则:S(A,C)≤S(A,B),S(A,C)≤S(B,C)。 上述条件意味着 μA-vA=μB-vB=μC-vC, μA+vA≤μB+vB≤μC+vC 因此 μA≤μB≤μC,vA≤vB≤vC⟹ 2μA-vA≤2μB-vB,2vA-μA≤2vB-μB 有 12D(A,B)=(2μB-vB)-(2μA-vA)+ (2vB-μB)-(2vA-μA)=(μB+vB)-(μA+vA) 同理,12D(A,C)=(μC+vC)-(μA+vA), 因此,D(A,B)≤D(A,C)⟹S(A,C)≤S(A,B) 同理,得到S(A,C)≤S(B,C)。 证毕 通过比较现有的18种相似度函数与本文提出的相似度函数,来说明本文方法的有效性,进而指出其他相似度函数可能存在的缺陷,具体如表2所示。 表2 IFS之间的各种相似度量方法比较 (1)如果A=〈0,0〉,B=〈0.5,0.5〉,C=〈1,0〉,依据记分函数和精确函数比较得A (2)如果A=〈0.3,0.4〉,B=〈0.3,0.3〉,C=〈0.4,0.4〉,D=〈0.4,0.3〉,依据本文的相似度模型,应有A (3)针对5、6和7、8,大部分文献和直观均认为前者相似度小于后者。如果A=〈0.4,0.2〉,B=〈0.5,0.3〉,C=〈0.5,0.2〉,依据投票模型,假设10人参与投票,A表示4人赞成,2人反对;B表示5人赞成,3人反对,C表示5人赞成,2人反对,投票结果表明A、B比A、C更为接近。由此可知本文改进的条件和提出的相似度与投票结果一致。同理,对于7、8也可以得出同样的结论。 (4)本文将用以下两种方式说明本文提出的相似度具有较强的区分能力,比现有文献有更高的优越性。 (i)假设μA和μB为变量,vA和vB固定值,运用Excel中模拟运算表功能,对提出的相似度进行模拟分析。 ①设vA=vB=0.1,分析结果如表3所示。行表示μA变化区间,列表示μB变化区间。 ②设vA=0.2,vB=0.5,结果如表4所示。 由表3和表4可知,当改变μA和μB时,相似度结果发生较为明显的变化,而且当固定μA或μB时,并没有出现相同的相似度比较结果,这说明本文提出的相似度测量方法具有较强的区分能力。 表3 当vA=vB=0.1时相似度比较结果 表4 当vA=0.2,vB=0.5时相似度比较结果 (ii) 比较本文的相似度与近几年文献中符合前5条性质相似度的方差。具体操作如下:首先用Excel随机生成500组IFSA与B,其中隶属度μ为区间[0,1]之间的随机数,使用函数rand(),而非隶属度v为区间[0,1-μ]之间的随机数,使用函数rand()*(1-μ);然后分别计算随机生成的IFS的相似度;最后得到500组随机IFS相似度的方差。此时模拟数据的方差基本接近其公式的方差。 表5 部分随机IFS的相似度 注:由于篇幅限制,仅显示20组随机IFS及其相似度。 其次,计算500组随机IFS相似度的方差,如表6所示。 表6 500组随机IFS相似度的方差 本文针对IFS相似度模型设计问题,从分析相似度模型的定义条件入手,研究各个相似度模型的匹配度。结合一般IFS的特征,运用记分函数来辨别不同IFS的大小关系,进而从内容和形式上定义一种新的直觉模糊相似度。并通过理论证明、算例分析说明提出的相似度能够满足原有性质和改进的性质,即从表2可知,尚未有一个相似度模型能满足已有的相似度条件和本文提出的相似度条件,而本文提出的相似度弥补了现有相似度存在的无法比较或者比较结果不合理的问题,灵敏度分析和模拟分析说明本文提出的相似度降低了信息损失,具有较强的区分度和辨别能力,可以更好地辅助决策者进行决策。 参考文献: [1] ATANASSOV K T. Intuitionistic fuzzy sets[J]. Fuzzy Sets & Systems, 1986, 20(1): 87-96. [2] CHEN S M. Similarity measures between vague sets and between elements[J]. IEEE Trans.on Systems Man & Cybernetics-Part B: Cybernetics, 1997, 27(1): 153-158. [3] HONG D H, KIM C. A note on similarity measures between vague sets and between elements[J]. Information Sciences, 1999, 115(1/4): 83-96. [4] FAN L I, ZHANG X U. Measures of similarity between vague sets[J]. Journal of Software, 2001, 12(6): 922-927. [5] LI Y, CHI Z, YAN D. Similarity measures between vague sets and vague entropy[J]. Journal of Computer Science, 2002, 29: 129-132. [6] LI D F, CHENG C. New similarity measures of intuitionistic fuzzy sets and application to pattern recognitions[J]. Pattern Recognition Letters, 2002, 23(1/3): 221-225. [7] LIANG Z Z, SHI P F. Similarity measures on intuitionistic fuzzy sets[J]. Pattern Recognition Letters, 2003, 24(15):2687-2693. [8] HUNG W L, YANG M S. Similarity measures of intuitionistic fuzzy sets based on Hausdorff distance[J]. Pattern Recognition Letters, 2004, 25(14): 1603-1611. [9] LIU H W. New similarity measures between intuitionistic fuzzy sets and between elements[J]. Mathematical and Computer Modelling, 2005, 42(1/2): 61-70. [10] HUNG W L, YANG M S. Similarity measures of intuitionistic fuzzy sets based on Lpmetric[J]. International Journal of Approximate Reasoning, 2006, 46(1): 120-136. [11] INTARAPAIBOON P. A hierarchy-based similarity measure for intuitionistic fuzzy sets[J]. Soft Computing, 2016, 20(5): 1909-1919. [12] BORAN F E, AKAY D. A biparametric similarity measure on intuitionistic fuzzy sets with applications to pattern recognition[J]. Information Sciences, 2014, 255(28): 45-57. [13] CHEN S M, CHANG C H. A novel similarity measure between Atanassov's intuitionistic fuzzy sets based on transformation techniques with applications to pattern recognition[J]. Information Sciences, 2015, 291(C):96-114. [14] CHEN S M, CHENG S H, LAN T C. A novel similarity measure between intuitionistic fuzzy sets based on the centroid points of transformed fuzzy numbers with applications to pattern recognition[J]. Information Sciences, 2016, s343-s344: 15-40. [15] XU Z S. Some similarity measures of intuitionistic fuzzy sets and their applications to multiple attribute decision making[J].Fuzzy Optimization & Decision Making,2007,6(2):109-121. [16] YE J. Cosine similarity measures for intuitionistic fuzzy sets and their applications[M]. Elsevier Science Publishers B. V., 2011. [17] SONG Y, WANG X. A new similarity measure between intuitionistic fuzzy sets and the positive definiteness of the similarity matrix[J].Pattern Analysis & Applications,2017(20):215-226. [18] IANCU I. Intuitionistic fuzzy similarity measures based on Frank t-norms family[J]. Pattern Recognition Letters,2014,42(1):128-136. [19] 袁宇, 关涛, 闫相斌, 等. 基于区间直觉模糊数相关系数的多准则决策模型[J]. 管理科学学报, 2014(4): 11-18. YUAN Y, GUAN T, YAN X B, et al. Multi-criteria decision making model based on interval-valued intuitionistic fuzzy number correlation coefficient[J]. Journal of Management Sciences in China, 2014(4): 11-18. [20] 王毅, 刘三阳, 张文, 等. 基于包含度的直觉模糊相似度量推理方法[J]. 系统工程与电子技术, 2014, 36(3): 494-500. WANG Y, LIU S Y, ZHANG W, et al. Intuitionistic fuzzy similarity measures reasoning method based on inclusion degrees[J]. Systems Engineering and Electronics, 2014, 36 (3): 494-500. [21] 王毅, 刘三阳, 程月蒙, 等. 基于倾向性的直觉模糊相似度量方法[J]. 系统工程与电子技术, 2015, 37(4):863-867. WANG Y, LIU S Y, CHENG Y M, et al. Intuitionistic fuzzy similarity measure approach based on orientation[J]. Systems Engineering and Electronics, 2015, 36(4): 863-867. [22] HWANG C M, YANG M S, HUNG W L, et al. A similarity measure of intuitionistic fuzzy sets based on the Sugeno integral with its application to pattern recognition[J]. Information Sciences, 2012, 189(6): 93-109. [23] MUKHERJEE S, BASU K. Solution of a class of intuitionistic fuzzy assignment problem by using similarity measures[J]. Knowledge-Based Systems, 2012, 27(4): 170-179. [24] BELIAKOV G, PAGOLA M, WILKIN T. Vector valued similarity measures for Atanassov’s intuitionistic fuzzy sets[J]. Information Sciences, 2014, 280: 352-367. [25] SONG Y, WANG X, LEI L, et al. A novel similarity measure on intuitionistic fuzzy sets with its applications[J]. Applied Intelligence, 2015, 42(2): 252-261. [26] FARHADINIA B. An efficient similarity measure for intuitionistic fuzzy sets[J]. Soft Computing, 2014, 18(1): 85-94. [27] NGUYEN H. A novel similarity/dissimilarity measure for intuitionistic fuzzy sets and its application in pattern recognition[J]. Expert Systems with Applications, 2016, 45(C): 97-107. [28] NGAN S C. An activation detection based similarity measure for intuitionistic fuzzy sets[J]. Expert Systems with Applications, 2016, 60: 62-80. [29] SONG Y, WANG X, QUAN W, et al. A new approach to construct similarity measure for intuitionistic fuzzy sets[J]. Soft Computing, 2017(1): 1-14. [30] HASSABALLAH M, GHAREEB A. A framework for objective image quality measures based on intuitionistic fuzzy sets[J]. Applied Soft Computing, 2017(57): 48-59. [31] IANCU I. Intuitionistic fuzzy similarity measures based on min-max operators[J]. Pattern Analysis & Applications, 2017(1): 1-10. [32] 龚艳冰, 丁德臣, 何建敏. 一种基于直觉模糊集相似度的多属性决策方法[J]. 控制与决策, 2009(9): 1398-1401. GONG Y B, DING D C, HE J M. Multi-attribute decision making method based on similarity measures of intuitionistic fuzzy sets[J]. Control and Decision,2009(9): 1398-1401. [33] DU W S, HU B Q. Aggregation distance measure and its induced similarity measure between intuitionistic fuzzy sets[J]. Pattern Recognition Letters, 2015, 60(C): 65-71. [34] ZHOU L, TAO Z, CHEN H, et al. Intuitionistic fuzzy ordered weighted cosine similarity measure[J]. Group Decision and Negotiation, 2014, 23(4): 879-900. [35] MENG F, CHEN X. Entropy and similarity measure of Atanassov’s intuitionistic fuzzy sets and their application to pattern recognition based on fuzzy measures[J]. Pattern Analysis and Applications, 2016, 19(1): 11-20. [36] 李鹏,朱建军,刘思峰.基于案例推理的直觉模糊决策方法[J].中国管理科学, 2015, 23(7): 113-118. LI P, ZHU J J, LIU S F. Intuitionistic fuzzy decision making methods based on case-based reasoning[J]. China Journal of Management Science, 2015, 23(7): 113-118. [37] CHEN S M, TAN J M. Handling multi-criteria fuzzy decision-making problems based on vague set theory[J]. Fuzzy Sets and System, 1994, 67(2):163-172. [38] HONG D H, CHOI C H. Multi-criteria fuzzy decision-making problems based on vague set theory[J]. Fuzzy and Systems, 2000, 114(1): 103-113.

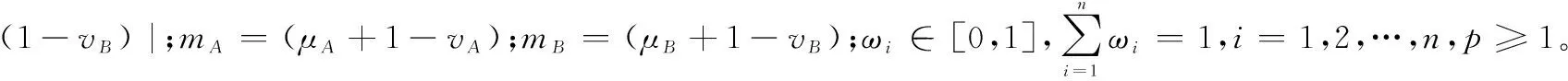
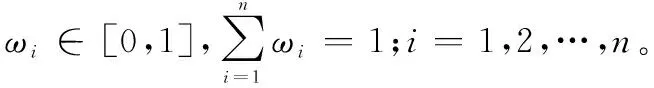

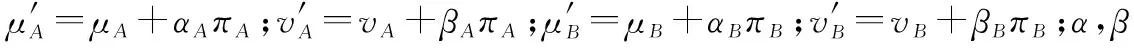
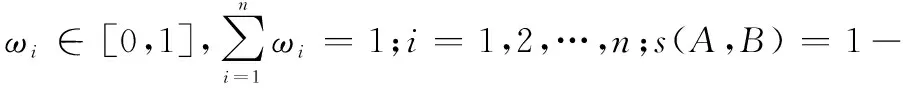
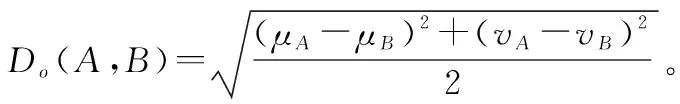


2 现有相似度函数分析

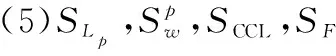

3 新的相似度函数设计
4 算例研究


5 结 论

