α稳定分布噪声下基于FHN模型的UWB-IR信号检测

蒋 磊, 陈博文,2, 张 群, 李 涛

(1. 空军工程大学信息与导航学院, 陕西 西安 710077; 2. 中国人民解放军95844部队, 甘肃 酒泉 735000)

0 引 言

超宽带冲激无线电(ultra wideband-impulse radio,UWB-IR)[1]是通过对超窄脉冲直接调制而得到的通信信号,与传统无线通信系统相比,超宽带通信具有高数据传输速率,发射功率低,抗干扰能力强与截获/检测概率特性低等优点[2]。因此,超宽带通信技术已被广泛运用于军事领域,美军已研制出UWB无人机高速数据链、UWB军用短波电台等军事通信装备[3]。但UWB信号具有超低的功率谱密度特性[4],致使其在强干扰环境中或远程传输时,信号往往被噪声所覆盖,检测难度高,对第三方进行全盲信号侦察带来了极大挑战。因此,在日益复杂的电磁环境下,UWB-IR信号的有效检测成为电子战领域亟待解决的问题。

在传统高斯白噪声条件下,针对UWB-IR信号检测,文献[5]提出一种基于FitzHugh-Nagumo(FHN)神经元模型随机共振的UWB-IR信号检测方法,可较好实现低信噪比(low signal-to-noise ratio,LSNR)条件下UWB-IR信号的有效检测。FHN神经元模型随机共振本质是通过噪声来放大强噪声背景中的微弱有效信号,从而实现对噪声的抑制。在传统FHN模型检测UWB-IR信号时,通常使用高斯分布描述背景噪声,然而,实际环境中的噪声或杂波常常是非高斯分布的,这类噪声持续时间短,幅值大,由不规则的尖峰或脉冲组成。α稳定分布[6]可以很好地模拟此类脉冲噪声,与实际数据更加吻合。但在脉冲噪声情况下,FHN模型系统性能将大大降低,因此,传统FHN模型检测方法不再适用非高斯分布噪声条件下的UWB-IR信号检测。

为抑制α稳定分布噪声,已有学者提出中值滤波[7],加权Myriad滤波[8]等多种去噪算法。但中值滤波无法充分利用有效信息,加权Myriad需理想信号作为参考,不适合全盲条件下信号检测。三倍分散系数准则[9]是一种适用于α稳定分布的异常值剔除准则,可剔除以α稳定分布的位置参数为中心一定区间外的异常数据。传统三倍分散系数准则中位置参数与分散系数为已知常数,但实际应用中这两个参数未知。鉴于此,本文将样本分位数法引入其中,提出一种新的三倍分散系数准则,首先使用样本分位数法估计位置参数与分散系数,再进行异常值剔除。结合改进的三倍分散系数准则与FHN模型,本文提出基于三倍分散系数-FHN模型的UWB-IR检测算法,首先对带噪UWB-IR信号进行异常值剔除,达到抑制脉冲噪声中强脉冲的目的,再通过FHN模型实现UWB-IR信号检测。仿真结果表明,本文所提算法能有效抑制α稳定分布的强脉冲噪声,较好地重构UWB-IR信号波形,可实现较低混合信噪比(mixed signal-to-noise ratio,MSNR)条件下UWB-IR信号的有效检测。

1 α稳定分布

α稳定分布是唯一满足广义中心极限定理的分布形式[10],高斯分布是其某一限制条件下的特例。与高斯分布相比,α稳定分布具有更厚重的拖尾,这一特性决定了α稳定分布具有显著脉冲特征,可以更好地吻合实际情况中复杂的噪声环境。α稳定分布不存在封闭的表达式,通常采用特征函数描述[11]为

φ(t)=exp{jμt-γ|t|α[1+jβsgn(t)ω(t,α)]}

(1)

式中

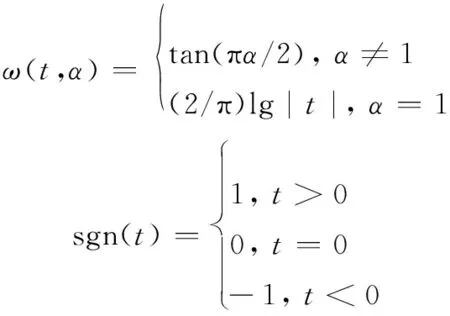
(2)

式中,α表示特征指数,用以表征其概率密度函数的拖尾厚重程度,随着α值的变小,函数拖尾越来越厚重,脉冲性越来越强;γ表示分散系数,表征α稳定分布的分散程度;β表示对称参数,用以表征α稳定分布的斜度,β=0时为对称α稳定(symnetricαstable, SαS)分布;μ表示位置参数,当0≤μ<1时,μ为α稳定分布中值,当1≤μ<2时,μ为其均值。当α=2时,α稳定分布为高斯分布;当0<α<2时,α稳定分布与高斯分布相似却又明显不同。α值越小,其统计分布上的拖尾越厚重,即远离样本均值或中值的样本数越多,故其时域存在较多的脉冲尖峰。图1为不同特征指数α时的SαS分布的概率密度函数曲线。图2为不同α值条件下SαS噪声对比图。从图2可以看出,随着α的减小,SαS拖尾越来越厚,信号的脉冲特性越来越强。

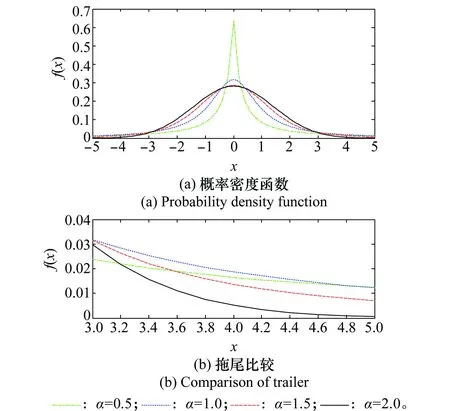
图1 SαS分布概率密度函数曲线Fig.1 Probability density function curve of SαS distribution

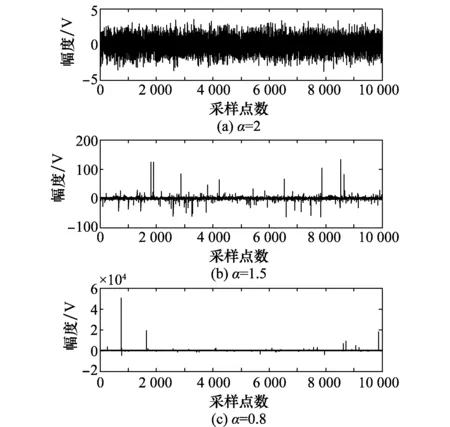
图2 不同α值条件下SαS分布噪声Fig.2 SαS distribution noise under different α

2 三倍分散系数-FHN模型

2.1 三倍分散系数准则

3En准则是一种常用且简单的异常值剔除准则,其中的置信度是描述测量位置位于某一区间内可靠程度的量,通常使用百分比表示;置信区间为选定的范围。通常使用标准差的倍数表示。由概率论与数理统计可知[12],若Ex为样本期望值,En为样本标准差,样本在区间[Ex-mEn,Ex+mEn]中随机出现的概率至少为(m2-1)/m2,当m>3时即可对异常值进行剔除。在α稳定分布中,期望与方差均未定义,其位置参数与分散系数分别对应于期望与标准差的意义,文献[9]中提出一种三倍分散系数异常值剔除准则,即以位置参数μ为中心,当样本超出[μ-3,μ+3]时剔除序列中的异常值,但文献[9]中的方法使用的位置参数与分散系数为已知量,实际情况中位置参数与分散系数的值为未知数,这极大限制了三倍分散系数准则的应用范围。鉴于此,本文提出一种改进的三倍分散系数准则,结合样本分位数法首先对α稳定分布的参数进行估计[13],再对序列异常值进行剔除。

(3)

i与d通过式(4)获得。

(n+1)f=i+d

(4)

式中,i为整数部分;d为小数部分。

分别定义以下4个统计量vα、vβ、vγ、vμ，即

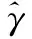
2.2 FHN神经元模型随机共振

FHN神经元模型随机共振[14]是在H-H模型基础上简化来的,由于随机共振独特的非线性特性,使信号、噪声与非线性系统达到协同,从而达到抑制噪声而放大有用信号的目的。

2.2.1 FHN神经元模型

FHN神经元模型表达式用方程组表示为

(5)

式中,x为快变恢复变量;y为慢变恢复变量;ε表示系统时间常数;A表示临界值,通常取0.01 mV;a和b均是系统常数,通常b取0.01;s(t)表示UWB-IR信号;n(t)表示α稳定分布噪声。求解式(5)所示方程时常采用四阶龙格-库塔算法。文献[5]研究表明,系统参数ε与a的值直接决定了FHN模型检测UWB-IR信号的检测效果,其值需随着待测信号的变化进行动态变化。

2.2.2 FHN神经元模型随机共振评价准则

通常以式(6)所示输入输出互相关函数来评判FHN模型随机共振的性能优劣[5],当该表达式取值最大时,实现最佳检测结果。

(6)

式中,η(t)表示带噪输入信号;R(t)是经FHN神经元模型得到的检测信号。

2.2.3 粒子群算法优化FHN模型系统参数

第2.2.1节中指出FHN模型的系统参数ε与a的值直接决定了其检测UWB-IR信号时检测效果,其值需随着待测信号的变化进行动态变化。鉴于此,本文选取粒子群优化(particle swarm optimization,PSO)[15]算法实现FHN模型系统参数的动态优化。

粒子群算法具体步骤如下:

步骤1种群初始化。m个粒子组成的种群记为X={x1,x2,…,xm},其中,第i个粒子的位置为xi={xi1,xi2},分别代表FHN模型中被优化的系统参数ε和a。初始化ε和a的取值范围分别为[εmin,εmax]和[amin,amax],在区间[0,1]上产生2个随机数作为第一个粒子x1,利用混沌搜索的遍历性与随机性,依据Logistic混沌映射作为初始粒子并建立种群,如式(7)所示,再将所有粒子映射到变量取值范围，如式(8)所示。

xi=4xi-1(1-xi-1)i=1,2,…,m

(7)

(8)

步骤2粒子速度与适应度初始化。对每个粒子的初始速度进行初始化为vi={vi1,vi2},i=1,2,…,m,根据式(6)计算每个粒子的初始适应度值,并初始化PBest与gBest,PBest={pBest1,pBest2，…，pBestm},表示各粒子目前搜索到的最优位置,gBest表示种群目前为止搜索到的最优位置,对应的适应度值分别为Pf={pf1,pf2,…,pfm}与gf。

步骤3粒子速度与位置更新。根据式(9)和式(10)更新粒子的速度与位置,计算新粒子对应的适应度值,并对PBest与gBest进行更新。

V=ω·V+c1γ1(pBest-present)+c2γ2(gBest-present)

(9)

present=present+V

(10)

式中,c1、c2为学习因子,通常取c1=c2=2;γ1与γ2为区间(0,1)均匀分布的随机数,present表示粒子当前的位置,ω为惯性权重,本文采用线性递减权重法,表达式如式(11)所示。

(11)

式中,t表示当前迭代数;T表示迭代总数;ωmax与ωmin分别表示惯性权重的最大值与最小值,一般取ωmax=0.9,ωmin=0.4。

步骤4若满足最大迭代数或误差要求时,得到的gBest即为FHN模型的最优系统参数ε与a。

2.3 三倍分散系数准则-FHN模型检测UWB-IR信号

由于α稳定分布噪声具有较强的非高斯脉冲特性,FHN模型受其强脉冲性影响性能急剧下降,无法实现UWB-IR信号的有效检测。三倍分散系数准则可以简单快速地剔除含α稳定分布噪声的UWB-IR信号中异常脉冲数据。因此在信号经过三倍分散系数准则处理后,再使用FHN模型对UWB-IR信号进行检测,以重构UWB-IR信号波形。流程如下所示。

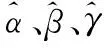
(2) 得到估计参数后,使用三倍分散系数准则对含噪UWB-IR信号进行异常值剔除。

(3) 经过异常值剔除处理后的信号使用第2.2.3节PSO算法优化的FHN模型进行信号检测,得到重构UWB-IR信号波形。

具体流程图如图3所示。

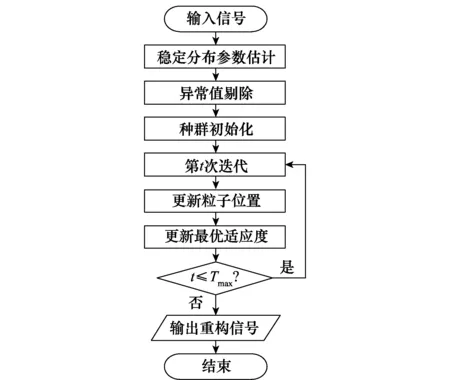
图3 本文所提算法流程图Fig.3 Flow chart of the proposed algorithm

3 仿真实验

α稳定分布噪声的二阶矩与更高阶矩是不存在的,仅在小于α阶时其阶数是有限的,因此传统高斯噪声条件下常用的信噪比(signal-to-noise ratio,SNR)中噪声的方差失去意义,因此重新定义MSNR为

MSNR=10lg{Var[s(t)]/γ}

(12)

式中,Var[s(t)]为UWB-IR信号的方差;γ为α稳定分布噪声的分散系数。

3.1 信号模型

本文仿真实验所选的UWB-IR信号表达式为

k∈{0,1,3,5,6,8}

(13)

式中,t=1∶1∶1 000 ns,高斯二阶导是冲激函数的参数分别为tn=3.5 ns,t0=8.51 ns；T=9.8 ns；A表示信号幅度。式(13)表示由高斯二阶导数所构成的非线性非平稳信号,当A=1时,信号波形如图4所示。

图4 UWB-IR信号Fig.4 UWB-IR signal

3.2 检测结果及分析

本文所提算法与加权Myriad滤波器和FHN模型检测算法分别进行对比,波形检测结果如图5所示。图5(a)为UWB-IR信号,其脉冲幅度A=0.95；图5(b)为α=1.5,β=0,γ=1,μ=0时含α稳定分布噪声的UWB-IR信号,此时MSNR=-12 dB；图5(c)为使用Myriad滤波方法的检测结果；图5(d)为仅使用FHN模型检测结果；图5(e)为使用本文所提方法的检测结果。

图5 检测波形比较Fig.5 Comparison of detection waveform

从图5可以看出,在强α稳定分布噪声干扰下,传统的Myriad滤波仅能进行信号序列平滑,无法实现UWB-IR信号波形恢复;FHN模型在α稳定分布噪声的强脉冲干扰下,检测性能急剧下降,重构波形失真严重,检测结果无法准确反映原始UWB-IR信号的脉冲信息;经过本文提出的改进的三倍分散系数准则进行异常值剔除后,再用FHN模型进行检测,检测结果与原始信号相比,脉冲信号的辨识度较高,能较为准确地反映UWB-IR信号中的脉冲位置信息,另外,随机共振独特的非线性特征放大了原始UWB-IR信号,因此,得到的检测信号幅值高于原始信号,这种特性进一步提高了检测性能。

为进一步说明本文所提算法对α稳定分布条件下UWB-IR信号波形恢复的有效性,本文引入均方根误差(root-mean-square error, RMSE)来衡量算法性能优劣,表达式为

(12)

式中,s(i)为原始UWB-IR信号;s′(i)为小波包降噪后的信号;n为信号长度。RMSE越小,表明重构信号与原始信号拟合度越高,检测性能越好。

分别使用加权Myriad滤波器,FHN模型与本文所提三倍分散系数准则-FHN模型对不同MSNR条件下的UWB-IR进行检测,每个SNR下仿真实验运行100次,记录RMSE均值,结果如图6所示,其中图6(b)是图6(a)的局部放大。

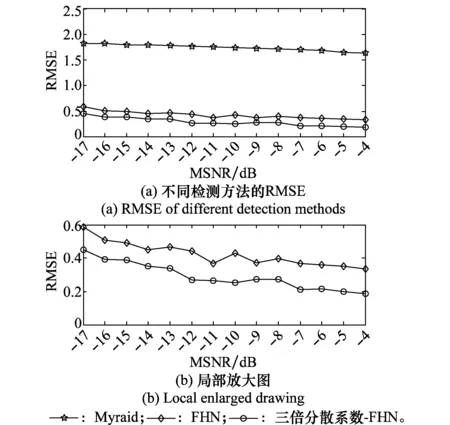
图6 检测所得RMSE对比Fig.6 Comparison of detection RMSE

从图6可以看出,在相同MSNR条件下,传统Myriad滤波对UWB-IR信号的检测性能最差,重构信号与原始信号差距较大; 由于FHN模型受α稳定分布噪声的影响较大,因此仅使用FHN模型得到的RMSE值仍然较高,对UWB-IR信号进行信号检测的性能仍然较差;但在经过本文改进的三倍分散系数准则处理后,再经FHN模型进行检测,所得检测结果明显优于其他2种方法。因此,改进的三倍分散系数准则有效抑制了α稳定分布强脉冲特性对FHN模型性能的影响,提高了FHN模型在α稳定分布条件下检测UWB-IR信号的能力。

为进一步验证本文所提算法的有效性,使用文献[16]中的分段相关平均对重构所得的信号进行门限判决,得到脉冲到达时刻,并计算到达时刻的差错率。分别使用Myriad滤波、FHN模型与本文所提算法在不同MSNR条件下进行仿真实验,每组实验进行100次,取平均值,结果如图7所示。

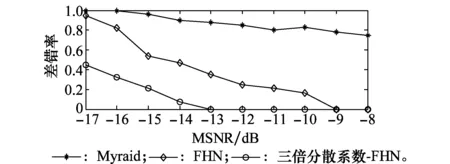
图7 差错率对比Fig.7 Comparison of error rate

从图7可以看出,在相同MSNR条件下,传统Myriad滤波所得的差错率最高,这是由于在较强α稳定分布噪声对UWB-IR信号重构的能力差,无法准确恢复其脉冲所在位置。受α稳定分布噪声的强脉冲特性影响,仅用FHN仍然不能较好地恢复信号波形,所得差错率仍然较高。但使用三倍分散系数准则-FHN模型方法所得重构信号与原始UWB-IR信号波形拟合度较高,因此该方法所得脉冲到达时刻差错率较低,在MSNR=-13 dB以上,可准确重构UWB-IR信号。此外,虽然三倍分散系数准则算法简单,运算速度快,在对带噪UWB-IR信号进行异常值剔除仍会带来算法复杂度少量提高与运算量少量增加。

4 结 论

针对α稳定分布噪声条件下传统FHN模型检测方法检测性能退化的问题,本文在传统FHN模型基础上,提出一种三倍分散系数-FHN模型的UWB-IR信号检测方法。此外,改进了传统三倍分散系数异常值剔除准则,克服了传统三倍分散系数准则对α稳定分布系数的先验条件依赖,使其更适合全盲条件下UWB-IR信号检测。信号经过改进的三倍分散系数准则进行异常值剔除,再经过FHN模型进行信号重构,实现α稳定分布噪声条件下UWB-IR信号检测。仿真实验表明,与传统Myriad滤波和仅用FHN模型检测方法相比,本文所提算法能有效抑制α稳定分布噪声,重构波形与原始波形拟合度较高,能较好地反映原始UWB-IR信号的波形特征与脉冲位置信息,检测SNR可达-13 dB,是一种适合强α稳定分布噪声条件下检测UWB-IR信号的新方法。

参考文献：

[1] JUNG Y A, SEO S I, YOU Y H. Two-stage preamble detection scheme for IR-UWB coexistence[J]. Wireless Personal Communic ations, 2017, 96(2): 3027-3039.

[2] 王方秋,张小飞,汪飞.IR-UWB系统中基于root-MUSIC算法的TOA和DOA联合估计[J].通信学报,2014,35(2):137-145.

WANG F Q, ZHANG X F, WANG F. Root-MUSIC-based joint TOA and DOA estimation in IR-UWB[J]. Journal on Communications, 2014, 35(2):137-145.

[3] WANG X, LIN L, TANG H, et al. Low power 3.1-10.6 GHz IR-UWB transmitter for Gbps wireless communications[J]. Science China Information Sciences, 2011, 54(5): 1094-1102.

[4] DENG H W, ZHAO Y J, FU F, et al. Compact and high isolation microstrip diplexer for GPS and UWB application[J]. Electeonics Letters, 2013, 49(10): 659-666.

[5] 刘潇文,蒋磊.基于FHN神经元模型的UWB信号检测方法[J].空军工程大学学报·自然科学版,2015,23(4):58-61.

LIU X W, JIANG L. Utlra-wideband signal detection based on FHN model method[J]. Journal of Air Force Engineering University (Natural Science Edition), 2015, 23(4):58-61.

[6] 张刚, 胡韬, 张天骐. Levy噪声激励下的幂函数型单稳随机共振特性分析[J]. 物理学报, 2015, 64(22):72-81.

ZHANG G, HU T, ZHANG T Q. Characteristic analysis of power function type monostable stochastic resonance with Levy noise[J]. Acta Physica Sinica, 2015, 64(22): 72-81.

[7] 李科,田社平,王志武.遗传算法加权中值滤波器的优化设计[J].中国计量学院学报,2008,19(1):56-60.

LI K, TIAN S P, WANG Z W. Optimum design of weighted median filters based on genetic algorithms[J]. Journal of China Jiliang University, 2008, 19(1):56-60.

[8] LIM H S, CHUAH T C, CHUAH H T. On the optimal Alpha-kcurve of the sample myriad[J]. IEEE Signal Processing Letters, 2007, 14(8):545-548.

[9] 金艳, 胡碧昕, 姬红兵.α稳定分布噪声下基于最优L-柯西加权的LFM信号参数估计[J]. 系统工程与电子技术, 2016, 38(7): 1488-1495.

JIN Y, HU B X, JI H B. Parameter estimation of LFM signals based on optimal L-Cauchy weighted method in α stable distribution noise[J]. Systems Engineering and Electronics, 2016, 38(7): 1488-1495.

[10] XIA N, WEI W, LI J, et al. A Kalman particle filtering algorithm for symmetric alpha stable distribution signals with application to HF time difference of arrival (TDOA) geolocation[J]. IET Signal Processing, 2016, 10(6): 619-625.

[11] 邱天爽, 戚寅哲. 稳定分布噪声下基于粒子滤波的双站伪多普勒定位方法[J]. 通信学报, 2016, 37(1): 28-34.

QIU T S, QI Y Z. Dual-station pseudo Doppler localization method based on particle filtering with stable distribution noise[J]. Journal on Communication, 2016, 37(1): 28-34.

[12] 盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 4版. 北京:高等教育出版社, 2008.

SHENG Z, XIE S Q, PAN C Y. Probability theory and mathema-tical statistics[M].4nd ed.Beijing:Higher Education Press, 2008.

[13] YU G, LI C, ZHANG J. A new statistical modeling and detection method for rolling element bearing faults based on alpha-stable distribution[J].Mechanical Systems & Signal Processing, 2013, 41(1/2):155-175.

[14] ZHANG J J, JIN Y F. Stochastic resonance in FHN neural system driven by non-Gaussian noise[J]. Acta Physica Sinica, 2012, 61(13):165-172.

[15] FONG S, WONG R, VASILAKOS A V. Accelerated PSO swarm search feature selection for data stream mining big data[J]. IEEE Trans.on Services Computing, 2016, 9(1):33-45.

[16] KIM D S, LEE S Y, HWANG T H, et al. A wireless sensor node processor with digital baseband based on adaptive threshold adjustment for emotional lighting system[J]. IEEE Trans.on Consumer Electronics, 2006, 52(4):1362-1367.