基于博弈理论的城市轨道PPP项目风险分担研究
,
(大连交通大学 交通运输工程学院,辽宁 大连 116028)
0 引言
城市轨道交通具有快速、安全、环保等优点,被大城市当做缓解交通压力的首选。但是城市轨道交通的建设成本大、运营成本高,政府的财政资金不能够满足其资金需求。公私伙伴关系(Public Private Partnership,PPP)模式由于能够减轻政府财政压力、提高运作效率、分散风险等优点[1],受到各大城市的青睐。但城市轨道PPP 项目参与方众多、生命周期长、项目的投资和运营成本高,使得项目参与方在项目中会遇到各种各样的风险[2],而某些风险很难仅仅依靠公私某一方来承担[3]。城市轨道交通PPP项目存在什么风险,如何合理分担这些风险,直接影响到项目的成败。
研究风险分担的方法有定性的也有定量的。定性的有问卷调查法和案例分析法等,定量的有马柯维茨模型和博弈模型等等。Li et al[4]基于风险偏好并采用问卷调查的定性方法对英国的PPP项目进行了风险分担分析。Abednego和Ogunlana[5]研究了印度尼西亚收费公路案例,提出和论证了其风险分担。杨秋波和侯晓文[6]运用马柯维茨模型确定了PPP项目中公共部门和私营机构最佳风险分担比例。Medda[7]基于博弈论建立了FOA模型,研究了交通项目PPP模式的融资风险分担问题,周鑫[8]为解决风险分担问题建立了轮流出价的讨价还价博弈模型。
分析后可发现,目前应用博弈理论的风险分担研究,大多数文献仅研究静态博弈或动态博弈一个类型。基于此,本文将风险分为独自承担和共担风险,分别使用静态和动态博弈来分析,最后综合考虑以确定风险分担结果。
1 博弈理论介绍
博弈论(Game Theory)又被称为对策论,是决策者为达到预期目标,在一定情况下,考虑其他人的可能行动,而对自己的行为和策略加以选择比较,从中选取对自己最有利或较为有利的策略并加以实施的过程。
运用博弈理论研究风险分担时,可以根据预期分担结果将分担过程分为两个层次,第一层运用静态博弈从众多风险中识别出需由公共部门和私营部门各自承担的风险、都不愿承担的风险以及需要共同承担的风险。然后运用第二层动态博弈模型来确认双方在需要共同承担的风险中的风险分担比例。静态博弈和动态博弈的区别就在于静态博弈模型用于整体风险分担研究,动态博弈模型用于不能整体分担的共担风险研究[9]。
使用博弈论进行风险分担,首先要明确相关要素和假设。
模型的基本要素有决策者、决策策略、效用函数。决策者就是指轨道交通PPP项目的政府部门和私人部门,即i=(1,2);决策策略指决策者根据相关信息和自己的风险癖好而采取的相关策略,即{可承担}或{不可承担};效用函数指的是项目决策者承担该风险时的结果,即其收益函数减去成本函数。
博弈模型的建立是基于以下几个假设:
(1)项目决策者都是理性的,都为了追求自身利益最大化,具有强烈的合作意愿;
(2)决策者的风险收益和成本都是可知的;
(3)时间是具有价值的,决策者的贴现因子是共同可知的[8];
(4)公共部门在信息上更加劣势,故先出价;
(5)风险分担时,公共部门的承担比例为k,私人部门的风险比例为1-k。
2 基于博弈的轨道PPP项目风险分担研究
2.1 轨道PPP项目风险识别和评估
城市轨道交通PPP项目的生命周期长、参与方众多,不仅有政府部门和私人部门的参与,其中还涉及贷款机构、保险机构、运营商等部门[10],所产生的风险遍及项目生命周期的各个时间段和各个项目进程。风险识别和评估是指通过对大量和项目有关的信息资料进行系统了解和分析,鉴别出项目中存在的现实和潜在的风险,并通过评估最终确定出风险中的关键因素、次要因素和一般因素。风险识别和评估是风险管理的第一步,也是最基础的。项目中的风险并不是一成不变的,在整个项目生命周期内,风险有可能随着时间以及项目进程的变化而变化,有的风险可能会消失,新的风险也可能会产生,所以对风险需要进行动态的、持续的和系统的识别。
2.2 轨道PPP项目风险分担流程和结果
城市轨道交通PPP项目中,政府部门和私人部门由于其经验和能力的不同,对不同类型的风险的控制能力也是不同的。所以为了使项目的整体收益最大化,需要对风险进行分担,以便将风险分配给最具控制力的一方,降低风险管理成本。轨道PPP项目风险分担流程见图1。
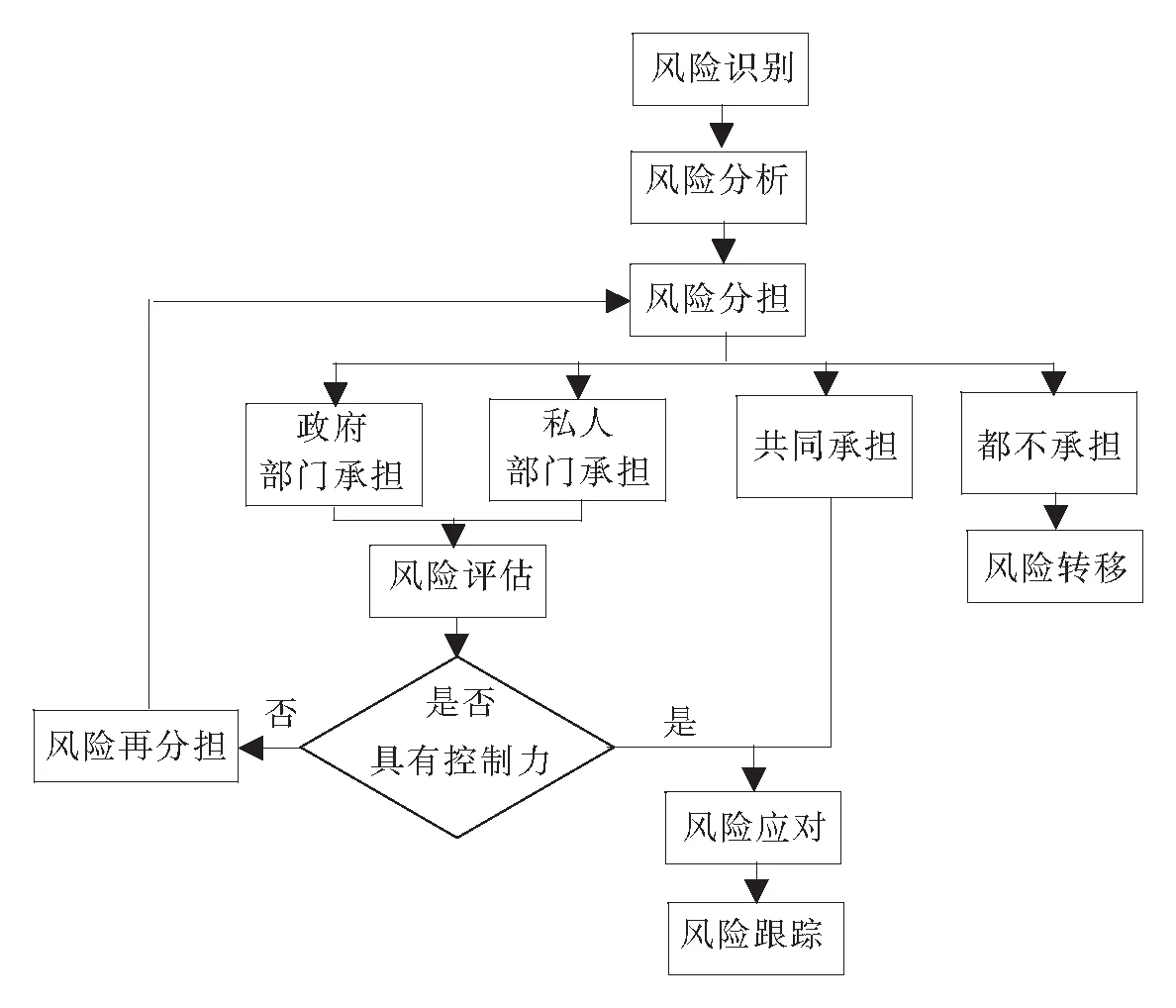
图1 轨道PPP项目的风险分担流程图
PPP项目的风险分担可划分为3个阶段:
(1)初始风险分担。初始风险分配对轨道项目进行风险识别后,根据相关资料以及专家的意见,初步判定在公共部门和私人部门的控制能力以内风险,以及控制能力以外的风险。控制能力以外的风险可以考虑将风险转移给保险公司等第三方机构;控制能力以内风险还要确定公共部门和私人部门是单独承担还是共同承担。
(2)分担结果谈判。对划分给公共部门和私营部门单独承担的风险,两者需要考虑对其是否具有最佳的控制能力,如果没有,就需要重新对该风险进行谈判。对于共担风险,公共部门和私营部门秉着项目整体利益最大化的原则,通过谈判,确定自己的承担比例。
(3)风险的跟踪和再分担。风险分担完成之后,公共部门和私营部门需要签订相关合同,然后在项目实施过程中需要实时地跟踪已知风险、监控其状态,防止发生意外,同时还要检测是否出现新的未知风险,如果出现,就需要对其进行风险的再分担。
2.3 对风险进行静态博弈分析
进行风险分担时,首先确认出单独承担的风险、共担的风险以及都不承担的风险。为准确反映完全信息下政府部门和私人部门对共担风险的分担情况,本文构建完全信息条件下静态风险分担博弈模型。
这里PPP 项目决策者就是轨道交通PPP项目的政府部门和私人部门,即i=(1,2),承担某一风险可得到风险收益ci,同时需要支付承担成本ci,承担风险的净收益为pi=yi-ci,ki为政府部门和私人部门承担风险的比例。
当政府部门和私人部门都选择承担某一风险时,其产出收益:P=k1p1+k2p2=k1(y1-c1)+k2(y2-c2)。
其它可同理得出。双方的静态博弈支付矩阵如表1所示,其均衡分析结果如表2。

表1 静态博弈支付矩阵
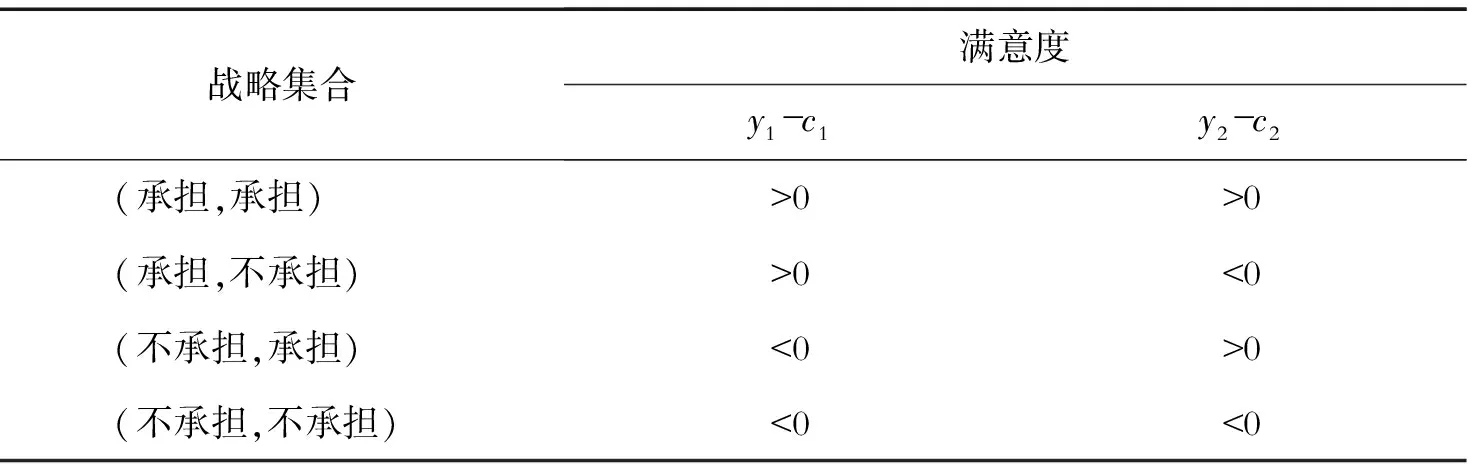
表2 风险博弈分析集合
在使项目的整体效用为正值的前提下,参与双方是否参与风险分担取决于其各自的效用,各种情况讨论如下:
(1)当y1-c1>0,且y2-c2<0时,公共部门的效用系数为正值,私营部门效用系数为负值,这种情况下,风险j由公共部门来承担[11]。同理当y1-c1<0,且y2-c2>0时,风险j由私营部门来承担。
(2)当y1-c1<0,且y2-c2<0时,公共部门和私营部门效用均为负值,即承担该风险后会产生损失,故双方都不愿意主动承担,此时可将此类风险转移给保险公司等其它机构承担,只有转移成本过大,超过双方的期望成本时,才会考虑由双方共同承担。
(3)当y1-c1>0,且y2-c2>0时,公共部门和私营部门的效用均为正值,双方承担风险均可以获得利益,故都希望承担该风险,即由决策者双方来共同承担该风险。
(4)当y1-c1=0或y2-c2=0时,表示公共部门和私营部门处于获利边缘,即该风险可承担也可不承担。
2.4 对风险进行动态博弈分析
经过上面静态博弈之后,可以得出需要共同承担的风险,接着要对共担风险进行风险分担博弈模型分析。Pi,Qi分别代表政府部门和私人部门在i次谈判中的分担比例。引入谈判损耗系数σi(i=1,2),谈判损耗系数是指双方谈判时付出的成本和代价,如谈判的机会成本、费用等。政府的谈判损耗系数也一定比私营资本大。由于私人部门相对于政府部门处于劣势,所以由公共部门首先提出报价,即分担比例。
首先政府提出政府承担风险比例为k1,私人部门的风险比例为1-k1,如果私人部门接受政府提出的分担比例,则双方博弈结束,风险分担比例为:政府部门:P1=k1;私人部门:Q1=1-k1。
如果私人部门对报价不认同,就进入第二阶段谈判,在第二阶段由私营部门重新提出报价,政府承担的风险比例为k2,私人部门的比例即为1-k2,如果政府部门接受该报价,博弈过程结束。由于第一次谈判没成功,在进行第二次谈判时就间接增加了谈判成本,此时需要考虑到损耗系数,所以其实际得到的分担比例是小于理论上应承担的分担比例。其最终风险分担比例为:政府部门:P2=σ1k2;私人部门:Q2=σ2(1-k2)。
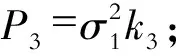
如果私人部门不接受,那么博弈过程就进入第四阶段,这样依次重复进行博弈,直到双方达成一致为止,如图2所示。
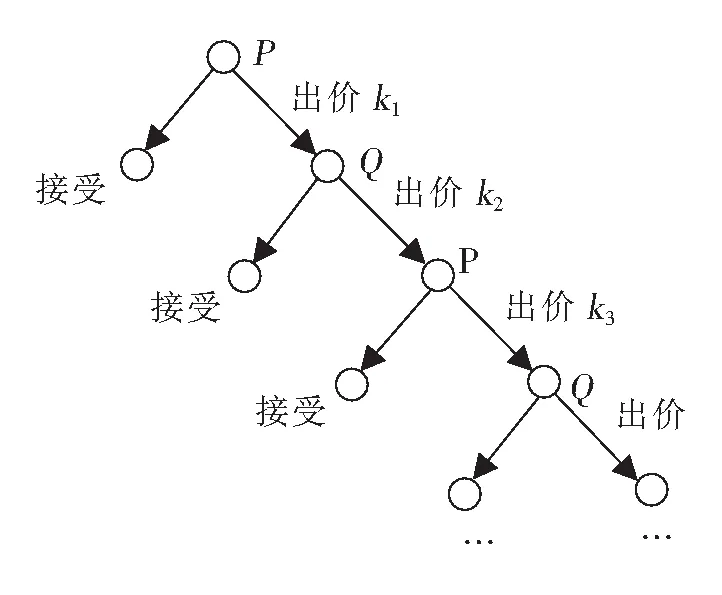
图2 讨价还价模型博弈树
夏克德(Shaked)和萨顿(Sutton)在1984年提出的如下理论:一个无限阶段的讨价还价博弈,不管是从第三回合逆推归纳开始,还是第一回合逆推归纳开始,其最终的结果都是一样的[12]。
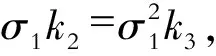
k2=σ1k3
(1)
同理,在第二次谈判中,政府部门得到的结果小于第一次谈判结果,所以为避免进入第二次谈判,减少损耗,使得自己承担风险最优,在第一次谈判时,政府部门的最优策略应为Q1=Q3,即1-k=σ2(1-k2),可得
k1=1-σ2+σ2k2
(2)
将式(1)代入式(2),可得
k1=1-σ2+σ1σ2k3
(3)
对于一个无限回合的讨价还价博弈来讲,设立的逆推基点不管是第三回合,还是第一回合,其最终的结果都是一样的。由此可得
k3=k1=1-σ2+σ1σ2k3
(4)
可得:k*=(1-σ2)/(1-σ1σ2),所以其最终分担结果为
政府部门承担风险的比例
P=(1-σ2)/(1-σ1σ2)
(5)
私人部门承担风险的比例
Q=1-P=σ2(1-σ1)/(1-σ1σ2)
(6)
这里假设双方的损耗系数可以通过问卷调查或者其风险收益率来表示,即公共部门的损耗系数为σ1=1/(1+r1),私营机构的损耗系数为σ2=1/(1+r2)。其中r1和r2分别表示公共部门和私营机构风险收益率[8,13]。
将r1和r2代入,可以得到:
政府部门承担风险的比例为
P3=(r2+r1r2)/(r1+r2+r1r2)
(7)
私人部门承担风险的比例为
Q3=r1/(r1+r2+r1r2)
(8)
2.5 对风险进行跟踪和再分担
风险再分担是指对项目进行中出现的新风险进行重新分担分析。政府部门和私人部门签订合同,实施PPP项目中,其风险防控是一个动态的过程,一些风险会消除,而一些新的风险会产生,为保证项目顺利实施,须对新产生的风险进行防控,即需要对PPP项目的风险进行风险跟踪和再分担[14],也就是严密监视已识别的风险,防止发生意外变化,同时监测是否产生新的未知风险,如果产生就需要对这个新风险进行风险评估和分担,即按照风险第一次分担阶段的方法评估和分担该风险[6]。
3 案例分析
某市地铁1号线路全长47.97 km,设车站30座,拟通过PPP模式解决政府的财政压力。通过风险识别和评估,确定出该项目的关键风险有准备风险、融资风险、建设风险、运营移交风险、政治风险、经济风险、法律风险、环境风险8大指标。通过对这些风险进行识别和评估,最终得出34个关键风险。
3.1 静态博弈分析
通过计算每个风险的承担成本和预期收益,得出风险的满意度。预期收益是指投资者承担某项风险而获取的收益,包括风险收益和风险补偿等。风险收益指投资者承担风险而能获取的期望收益;风险补偿指投资者承担风险而获取的政府的相关优惠和补助等等。
风险成本指为获取收益、规避风险,投资者往往要花费一些必要的成本费用,包括调查成本、机会成本、监督成本和激励成本等。调查成本,为降低投资风险而进行的相关调查支付的成本。机会成本,因承担某项风险而耽搁掉相当的另一投资或贷款项目的收益。监督成本,投资者通过对风险的监控、监督而支付的成本。激励成本,为更大程度控制风险,为投资人谋利益,投资者采用提供高薪、奖金、股票期权、优先股奖励等措施付出的成本。
以共担风险市场需求变化为例。假设政府部门的各种承担成本和为400万元,其预期收益为512万元,所以其对该风险的满意度为512-400=112万元。私人部门的承担成本为300万元,其预期收益为450万元,其对该风险的满意度为450-300=150万元。政府部门和私人部门的满意度都为正,所以该风险需共同承担。具体风险分担结果如表3所示。
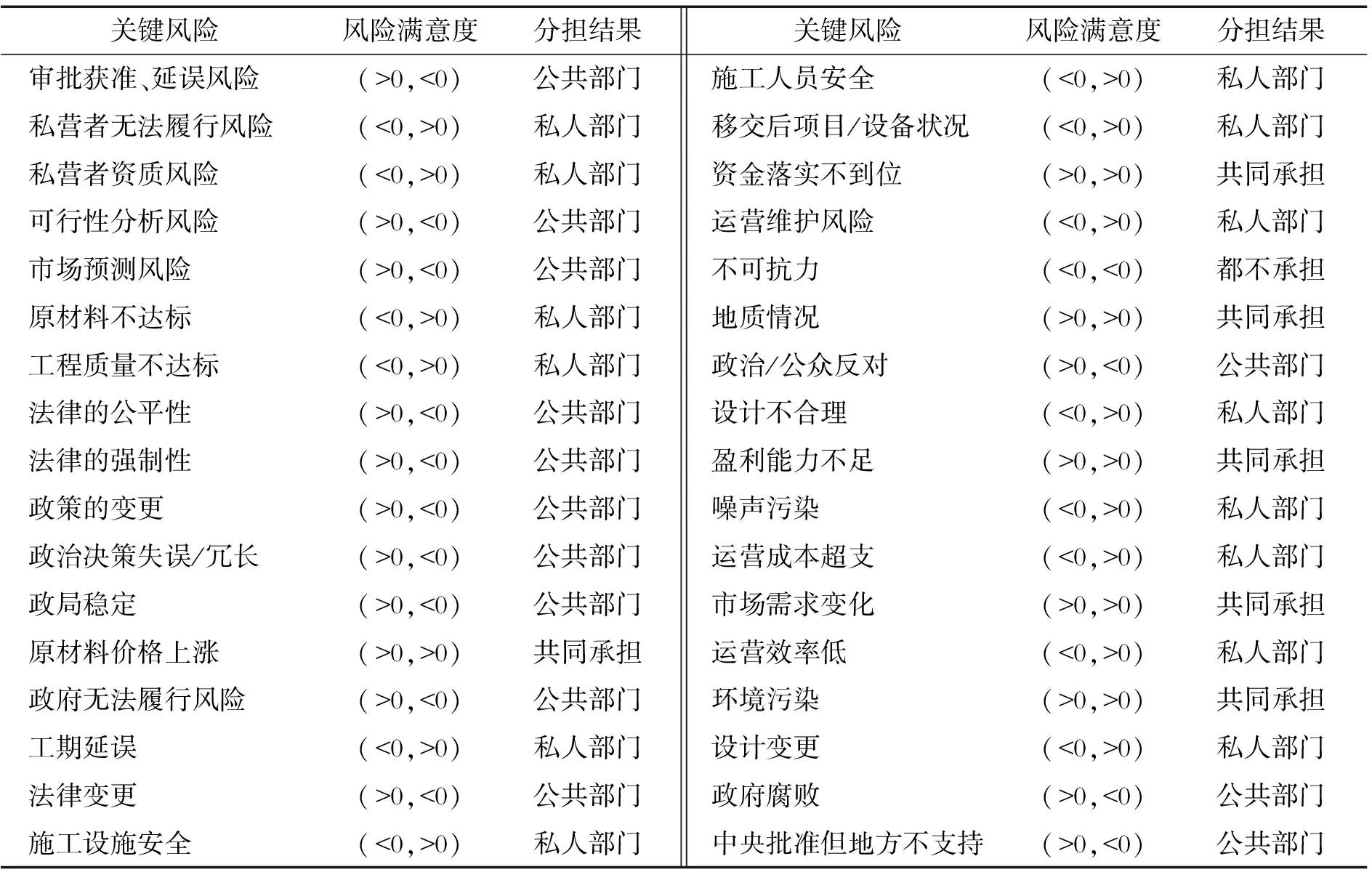
表3 关键风险分担表
3.2 动态博弈分析
谈判损耗系数代表了在讨价还价的力量大小。可以从以下几个方面对其进行确定:时间价值,即谈判时间对谈判方的价值。机会成本, 即能找到相似或相同成交条件的可能性的大小。谈判成本, 即每一次谈判花费的费用。假设双方的损耗系数可以通过风险收益率来表示。
通过面谈以及问卷调查的方式,对多名专家和学者进行问卷调查,对得到的数据进行统计和分析,对每一个风险的每一个风险收益率求平均值,进而得到讨价还价过程中完全信息条件下的谈判损耗系数。再根据式(7)和式(8),可得政府部门和私营部门承担风险的比例。以市场需求变化为例,假设公共部门和私营部门对风险市场需求变化的风险收益率分别为25%和36%,可得:
其它共担风险的分担比例也同样得出。
4 结语
近年来, PPP模式由于能减轻政府财政压力、提高运作效率、分散风险等优点,在我国的基础设施领域得到广泛的应用。城市轨道交通PPP项目面临更多的潜在风险。本文根据预期的分担结果,构建一个将静态博弈和动态博弈结合的风险分担模型,对于通过计算得出的风险收益和风险成本,使用静态博弈模型,根据满意度把相关风险分类为单方承担、都不承担和共同承担,对于需要共同承担的风险,采用动态模型分析承担比例,并采用具体案例进行论证,从而得出公私双方对于该项目风险分担的比例。
参 考 文 献
[1]郑志强,陶长琪,冷毅.大型体育设施供给PPP模式的合作博弈分析[J].体育科学.2011,31(5):27-32.
[2]Xiao HuaJin,Hemanta Doloi .Interpreting risk allocation mechanism in public-private partnership projects: an empirical study in a transaction cost economics perspective[J].Construction Management & Economics,2008,26(7):707-721.
[3]葛果,侯懿.基于风险偏好的PPP项目风险分担的三方博弈模型[J].四川理工学院学报:自然科学版,2015,28(1):87-91.
[4]Li B,Akintoye A,Edwards P J,et.al.The allocation of risk in PPP/PFI construction projects in the UK[J]. International Journal of Project Management,2005,23(1):25-35.
[5]Abednego M P,Ogunlana S O.Good project governance for proper risk allocation in public-private partnerships in Indonesia[J]. International Journal of Project Management,2006,24(7):622-634.
[6]杨秋波,侯晓文.PPP模式风险分担框架的改进研究[J]. 项目管理技术,2008,6(8):13-17.
[7]Medda F.A game theory approach for the allocation of risks in transport public private partnerships[J]. International Journal of Project Management,2007,25(3):213-218.
[8]周鑫.项目融资风险分担博弈分析[J]. 合作经济与科技, 2009(14):78-79.
[9]朱向东,肖翔,征娜.基于三方博弈模型的轨道交通PPP项目风险分担研究[J].河北工业大学学报,2013,42(2):97-101.
[10]贾丽丽,和鑫,王辉.城市轨道交通PPP融资模式风险评价研究[J].石家庄铁道大学学报:社会科学版,2013,7(4):29-33.
[11]孙振正.PPP模式下基础设施项目融资风险管理研究[D].上海:华东理工大学,2011.
[12]李林,刘志华,章昆昌.参与方地位非对称条件下PPP项目风险分配的博弈模型[J].系统工程理论与实践,2013,33(8):1940-1948.
[13]丁红红.基于博弈论的供应链管理中企业合作问题的研究[J].石家庄铁道大学学报:社会科学版,2009,3(3):20-24.
[14]刘新平,王守清.试论PPP项目的风险分配原则和框架[J].建筑经济,2006(2):59-63.

