分数阶不确定Duffling混沌系统的终端滑模同步
毛北行,周长芹
(郑州航空工业管理学院理学院,河南 郑州 450015)
分数阶系统大量存在于现实世界,并激起了众多爱好者的极大兴趣.[1-4]考虑分数阶系统的滑模控制是极具挑战性的控制课题,故其引起了学者们的密切关注.[5-11]文献[12]利用适应控制方法研究了具有终端角度约束的滑模制导律;文献[13]基于滑模方法研究了Rössler系统的同步问题;文献[14]利用滑模方法研究了分数阶振子网络的同步;文献[15]基于滑模控制研究了分数阶异结构混沌系统的同步问题;文献[16]基于滑模控制研究了分数阶金融系统的同步.本文研究了不确定分数阶Duffling混沌系统的终端滑模同步,获得了分数阶不确定Duffling系统的主从系统取得滑模同步的充分条件.
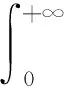
定义1[17]Caputo分数阶导数定义为
1 分数阶不确定Duffling系统的滑模同步
以分数阶不确定Duffling混沌系统作为主系统
(1)
系统参数a=-1,b=0.25,c=0.5,ω=1,α=0.873时系统呈现混沌态.从系统设计为
(2)
假设1Δg(y1,y2)+d(t)=f(t).
假设2|f(t)|≤M|e2(t)|.
假设3e2(t)=0时,f(t)=0,e2(t)≠0时,f(t)≠0.
假设40 定义ei=yi-xi(i=1,2),得到误差方程 不在滑模面上时,构造Lyapunov函数 则: s(t)[-M|e2|sgns-ηsgn(s(t))+f(t)]≤ 由引理2,s(t)→0. 假设5存在m,n>0,使得|Δg(y1,y2)| 定义ei=yi-xi(i=1,2),可得误差系统为 (3) 设计分数阶终端滑模函数 (4) 定理2在分数阶非奇异滑模面(4)上,系统误差(3)的轨迹能在有限时间内趋于原点. 设计控制器为双幂次趋近律 (5) 其中k1>0,k2>0,γ>1,0<μ<1. 定理3在满足假设5的条件下,如果构造控制器(5),则误差系统(3)的轨迹能达到滑模面. 由假设条件5可得 根据引理2,s(t)→0. 利用Matlab进行数值仿真,取系统参数a=-1,b=0.25,c=0.5,ω=1,α=0.873. 定理1中设计Δg=-0.05siny1,d(t)=0.2cos(t),η=2.设置系统初始值为(x1(0),x2(0))=(0.1,0.2),(y1(0),y2(0))=(0.5,-0.6).控制律 定理3中选取参数r=1.5,λ=6,k1=10,k2=4,γ=2,μ=0.5.设计 设计新型双幂次趋近律来设计控制律为 该趋近律收敛速度较快.设置系统初始值为(x1(0),x2(0))=(0.1,0.2),(y1(0),y2(0))=(-1.6,-0.55),其系统误差如图2所示. 从图1—2可以发现:定理1中t>0.264 s以后,系统误差逐渐趋于零,表明系统达到同步;定理3中t>0.237 s以后,误差逐渐趋于坐标原点,系统取得同步化;定理3达到同步所需时间较定理1少,系统更快趋于同步,表明采用双幂次趋近控制律控制效果良好. 图1 定理1中系统的误差曲线 研究了分数阶不确定Duffling混沌系统的滑模同步问题,构造分数阶滑模函数和控制律可以使驱动-响应系统滑模达到混沌同步.仿真实例验证了方法的正确性. [参 考 文 献] [1] MOHAMMOD P A.Robust finite-time stabilization of fractional-order chaotic systems based on fractional Lyapunov stability theory[J].Journal of Computation and Nonlinear Dynamics,2012(7):1011-1015. [2] MILAD MOHADESZADEH,HADI DELAVRI.Synchronization of fractional order hyper-chaotic systems based on a new adaptive sliding mode control[J].Int J Dynam Control,2015,10(7):435-446. [3] WANG X,HE Y.Projective synchronization of fractional order chaotic system based on linear separation[J].Phys Lett A,2008,37:435-441. [4] 马珍珍,肖剑,杨叶红.一类具有二次项的新分数阶Mavpd混沌系统[J].武汉大学学报(工学版),2014,47(2):276-285. [5] MOHAMMOD P A,SOHRAH K,GHASSEM A.Finite-time synchronization of two different chaotic systems with unknown parameters via sliding mode technique[J].Applied Mathematical Modeling,2011,35(6):3080-3091. [6] MANDELBROT B B,VAN NESS J W.Fractional Brownian motions fractional noises and applications[J].SIAM Review,1968,10(4):422-437. [7] BAGLEY R L,TORVIK P J.On the appearance of the fractional derivative in the behavior of real materials[J].J Appl Mech,1984,51(4):294-298. [8] SHAHIRI M,GHADRI R,RANJBARN,et al.Chaotic fractional-order coullet system:synchronization and control approach.[J].Commun Nonlinear Sci Numer Simul,2010,15:665-674. [9] HAMAMCI,KOLKSAL M.Calculation of all stabilizing fractional-order PD controllers for integrating time delay systems.[J].Comput Math Appl,2010,15:1267-1278. [10] MATOUK A.Chaos feedback and synchronization of fractional-order modified autonomous Van der pol-Duffling circuit[J].Commun Nonlinear Sci Numer Simul,2011,16:975-986. [11] 丁金凤,张毅. 基于按指数律拓展的分数阶积分的El-Nabulsi-Pfaff 变分问题的Noether 对称性[J].中山大学学报(自然科学版),2014,54(6):150-154. [12] 赵斌,周军,卢晓东,等.考虑终端角度约束的自适应积分滑模制导律[J].控制与决策,2017,32(11):1966-1972. [13] 孙宁,叶小岭,刘波.Rössler 混沌系统的自适应滑模控制[J].计算机仿真,2014,31(8):382-386. [14] 毛北行,王东晓.分数阶Van der pol振子网络的混沌同步[J].华中师范大学学报(自然版),2016,50(2):202-205. [15] 毛北行,李巧利.分数阶参数不确定系统的异结构混沌同步[J].中国海洋大学学报(自然版),2017,47(7):149-152. [16] 朱涛,张广军,姚宏,等.滑模控制的时滞分数阶金融系统混沌同步[J].深圳大学学报(理工版),2014,31(6):626-629. [17] PODLUBNY.Fractional differential equation[M].San Diego:Academic Press,1999:715-719. [18] 梅生伟,申铁龙,刘志康.现代鲁棒控制理论与应用[M].北京:清华大学出版社,2003:84-146.
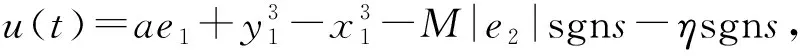
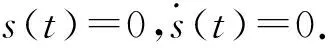
-M|e2||s(t)|+M|e2||s(t)|-η|s(t)|=-η|s(t)|<0.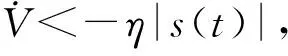
2 分数阶不确定Duffling系统的终端滑模同步

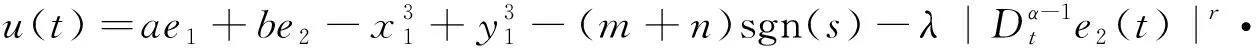
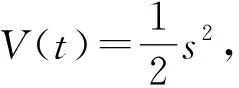
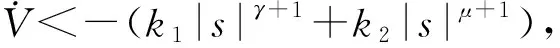
3 数值仿真
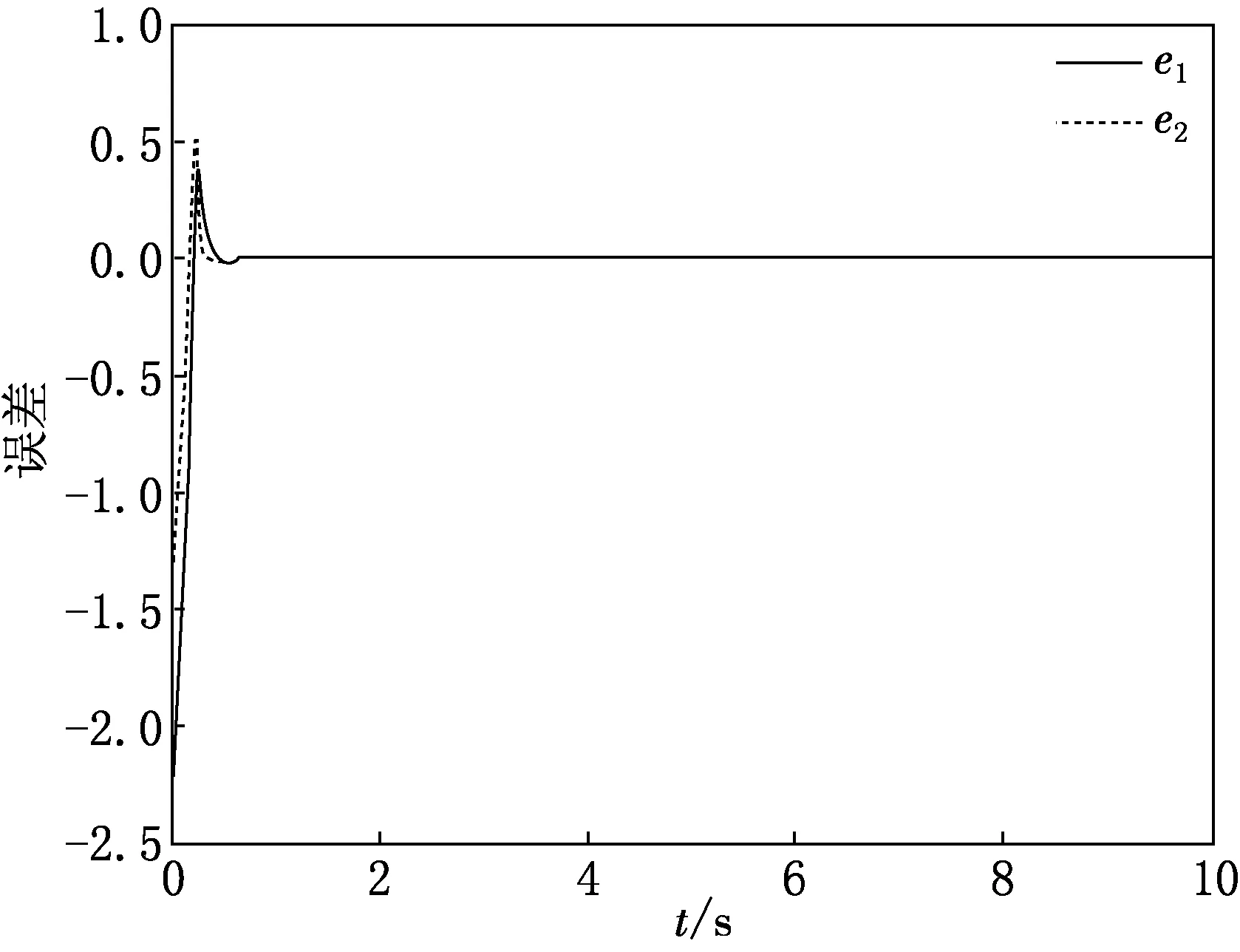
4 结论

